please help me with this its timed first person to give me correct answer gets 25 points

Answers
Answer:
8. 14 for the third question.
9. 18 for the forth question.
Step-by-step explanation:
the third and forth orange equations.
Related Questions
A jar contains 8 red marbles 14 blue marbles, 11 yellow marbles, and 6 green marbles. If a marble is selected at random, what is the probability that it will be green?

Answers
Because 6/39 are green marbles, then simplify 6/39 which is 2/13.
The graph of y = 4x? - 4x - 1 is shown.
Use the graph to find estimates for
the solutions of
i) 4x2 - 4x - 1 = 0
1%C
ii) 4x2 - 4x - 1 = 2

Answers
Then the two solutions are: x = (4 + 5.66) / 8 = 11.2075 and x = (4 - 5.66) / 8 = -0.2075
What is meant by Bhaskara's equation?The sine approximation formula of Bhaskara I is a rational equation in one variable for computing the approximations of the trigonometric sines found by Bhaskara I (c. 600–c. 680), an Indian mathematician of the seventh century.
Indian astronomer and mathematician Bhaskara II lived in the 12th century. He created a number of the same foundations and findings that are entirely attributable to Europeans and are still very helpful in modern science and forecasts, such as a basic form of calculus.
Here we have the equation:
y = 4 × x² - 4 × x - 1
And the graph should be available (you can see it below this answer)
Now, we're seeking answers to:
4 × x²- 4 × x - 1 = 0
The two x values at which the graph of our function intersects the y = 0 line, or the x-axis, will be these solutions.
The next step is to identify the two x values where our graph crosses the x-axis.
We can estimate the solutions in the graph as follows:
x = -0.2
x = 1.2
The Bhaskara's equation can be used to determine the precise solutions, and we will discover that the solutions are provided by:
\($x=\frac{-(-4)+-\sqrt{(-4)^2-4 * 4 *(-1)}}{2 * 4}=\frac{4+-\sqrt{32}}{8}=\frac{4+-5.66}{8}\)
Then the two solutions are:
x = (4 + 5.66) / 8 = 11.2075
x = (4 - 5.66) / 8 = -0.2075
To learn more about Bhaskara's equation, refer to:
https://brainly.com/question/24334139
#SPJ1

I need help with 2 math questions ASAP- Marking brainiest answer plus 20 points. I will insert a picture of the following questions.
For question number 1. You’ll need to find the area of top rectangle, area of bottom rectangle, total area of figure.
The 2nd question you’ll need to find area of shaded region. As you can see when it’s correct it changes colors.
I hope you have a blessed day and life for whoever helps me with this.

Answers
Answer:
Area is a measure of how much space there is inside a shape. Calculating the area of a shape or surface can be useful in everyday life – for example you may need to know how much paint to buy to cover a wall or how much grass seed you need to sow a lawn.
This page covers the essentials you need to know in order to understand and calculate the areas of common shapes including squares and rectangles, triangles and circles.
Step-by-step explanation:
I think
Find the area of the rectangular field in hectares whose length and breadth are 400 m and 125 m.
Answers
Answer:
50,000 m²
Step-by-step explanation:
PLS HELP ILL MARK AS BRAINLIEST

Answers
Answer:
296, 288, 280, 240
Step-by-step explanation:
y = -8x + 296 is a linear equation by which you're plugging the x values of 0,1,2,7 into it to get a y value.
y = 296 when x = 0,
y = 288 when x = 1,
y = 280 when x = 2,
y = 240 when x = 7.
Cheers!
find the buying price when 5% sales tax is added on the purchase of 5kg of wheat at 20 per kg
Answers
Answer:
$300
Step-by-step explanation:
5% of x + 5 kg = 20
0.05 * x + 5 = 20
0.05x + 5 = 20
0.05x = 20 - 5
0.05x = 15
x = 15 / 0.05
x = $300
Marital status can be categorized into: never married, married, widowed, or divorced. According to Infoplease, the following are the probabilities of those marital status categories for adults in the United States (data from 2000):
Marital Status Never Married Married Widowed Divorced
Probability 0.239 0.595 0.068
Required:
According to the information in the table, what is the probability that a randomly chosen US adult is divorced?
Answers
According to the information in the table, the probability that a randomly chosen US adult is divorced is 0.068.
According to the provided information, the table shows the probabilities of different marital status categories for adults in the United States. The probability values indicate the likelihood of an adult falling into each category.
In this case, the probability listed for the "Divorced" category is 0.068. This means that out of the total adult population in the United States, approximately 6.8% are classified as divorced. Therefore, if a US adult is chosen randomly, there is a 0.068 probability (or 6.8% chance) that they will be classified as divorced based on the data from the year 2000.
To know more about probability,
https://brainly.com/question/14093728
#SPJ11
Type the integer that makes the following subtraction sentence true:
8 − ?= –1
Answers
Answer:
9
Step-by-step explanation:
Since the value is negative, that means that missing integer has to be 1 greater than 8 to make -1. 1 more than 8 is 9. Hope this helps! If you are still confused, please comment!
Jacque needs to buy some pizzas for a party at her office. She's ordering from a restaurant that charges a \$7.50$7.50dollar sign, 7, point, 50 delivery fee and \$14$14dollar sign, 14 per pizza. She wants to buy as many pizzas as she can, and she also needs to keep the delivery fee plus the cost of the pizzas under \$60$60dollar sign, 60. Each pizza is cut into 888 slices, and she wonders how many total slices she can afford. Let PPP represent the number of pizzas that Jacque buys.
Answers
Answer:
30slicesStep-by-step explanation:
given data
cost of pizza $7.5
cost of delivery=$14
let the the number of pizza be p
let the total cost of x pizza be y
the expression for the total cost of x pizza is
y=7.5+14p
given that y=$60
60=7.5+14p
solving for x we have
14p=60-7.5
14p=52.5
p=52.5/14
p=3.75
therefore the total slices is
3.75*8= 30slices
help me solve this pls! (For 25 points)

Answers

Question from Venn diagram solving... plz solve. Worth 15 points

Answers
Answer:
For this type of problem, it is best to use Venn diagrams as shown in the picture. The areas where the circles intersect are the mutual events that occur together. The area where all circles intersect is denoted as x. These are the students who play all sports. Assuming all of the students play sports in the school, all of the numbers in the circles should add up to 405. The remaining area would be the difference. The solution is as follows:
Students who play tennis and hockey: 45 - x
Students who play hockey and softball: 60 - x
Students who play only tennis and softball: 39 - x
Students who only play tennis:
251 - 45 + x - 39 +x -x = x + 167
Students who only play hockey:
157 - x - 45 + x - 60 + x = x + 52
Students who only play softball:
111 - x - 60 + x - 39 + x = x + 12
The sum of all of these should be 405:
45-x+60-x+39-x+x+167+x+52+x+12 = 405
Solving for x,
x = 30
Therefore, there are 30 pupils who play all sports; 15 pupils who play tennis and hockey; 30 pupils who play hockey and softball; 9 pupils who play tennis and softball; 197 pupil who only play tennis; 82 pupils who only play hockey; and 42 pupils who only play softball.
Step-by-step explanation:
Hope this is correct, if it is wrong then please feel free to critique me and I wil correct my mistake(s). I'm sorry in advance if it is incorrect.
Find an equation of the tangent plane to the parametric surface x=−1rcosθ x = − 1 r cos θ , y=−3rsinθ y = − 3 r sin θ , z=r z = r at the point (−12‾√,−32‾√,2) ( − 1 2 , − 3 2 , 2 ) when r=2 r = 2 , θ=π/4 θ = π / 4 .
Answers
The equation of the tangent plane is obtained as x + 3y - 4√2 = 0.
What is an equation?
A mathematical definition of an equation is a claim that two expressions are equal when they are joined by the equals sign ("=").
To find the equation of the tangent plane, we need to find the partial derivatives of the given parametric equations with respect to x and y, and evaluate them at the given point.
∂x/∂u = -cosθ, ∂y/∂u = -3sinθ, ∂z/∂u = 0
At the point (-√2, -3√2, 2), we have -
∂x/∂u = -cos(π/4) = -1/√2, ∂y/∂u = -3sin(π/4) = -3/√2, ∂z/∂u = 0
So the normal vector to the tangent plane at this point is -
N = (-1/√2, -3/√2, 0)
The equation of the tangent plane can be written as -
(-1/√2)(x + √2) + (-3/√2)(y + 3√2) + 0(z - 2) = 0
Simplifying this equation, we get -
-x/√2 - 3y/√2 + 2√2 = 0
Multiplying both sides by √2, we get -
-x - 3y + 4√2 = 0
So the equation of the tangent plane to the given parametric surface at the point (-√2, -3√2, 2) when r=2, θ = π/4 is -
x + 3y - 4√2 = 0
Therefore, the equation is x + 3y - 4√2 = 0.
To learn more about equation from the given link
https://brainly.com/question/28871326
#SPJ1
To conduct a test of hypothesis with a small sample, we make an assumption that?
Answers
To conduct a test of hypothesis with a small sample, we make an assumption that the population is normally distributed .
What is normal distribution?
A probability distribution that is symmetric about the mean is the normal distribution, sometimes referred to as the Gaussian distribution. It demonstrates that data that are close to the mean occur more frequently than data that are far from the mean.
The normal distribution appears as a "bell curve" on a graph.
A probability bell curve is more properly described as the normal distribution.The mean and standard deviation of a normal distribution are 0 and 1, respectively. It has a kurtosis of 3 and zero skew.Not all symmetrical distributions are normal, but all normal distributions are symmetrical.Natural occurrences frequently resemble the usual distribution.To know more about normal distribution........
https://brainly.com/question/4079902
#SPJ4
The slope of the line is-
A)m=-2
B)m=-(1/2)
C)m=1/2
D)=m=2
A point on the line is-
A)(-4,-1)
B)(4,1/2)
C)(1/2,-1)
D)(1,4)

Answers
Answer:
C
D
Step-by-step explanation:
Point slope form is written in
y - y1 = m(x - x1)
Where m is the slope and (x1, y1) is a point on the line.
Looking at the values we have m = 1/2 and x1 = 1, y1 = 4.
Therefore the slope is 1/2 and the point is (1,4)
The initial value of function f(s) = 4(s+25) / s(s+10) at t = 0 is..
a. 10
b. 4
c. 0 d. [infinity]
Answers
The initial value of the function f(s) = 4(s+25) / s(s+10) at t = 0 is 4 (option b).
The initial value of a function is the value it takes when the independent variable (in this case, 's') is set to its initial value (in this case, 0). To find the initial value, we substitute s = 0 into the given function and simplify the expression.
Plugging in s = 0, we get:
f(0) = 4(0+25) / 0(0+10)
The denominator becomes 0(10) = 0, and any expression divided by 0 is undefined. Thus, we have a situation where the function is undefined at s = 0, indicating that the function has a vertical asymptote at s = 0.
Since the function is undefined at s = 0, we cannot determine its value at that specific point. Therefore, the initial value of the function f(s) = 4(s+25) / s(s+10) at t = 0 is undefined, which is represented as option d, [infinity].
Learn more about expression here:
https://brainly.com/question/28170201
#SPJ11
A carton of grapefruit juice displays the nutritional information shown below. How many grams of sugar are there in a 200 ml glass of juice? Grapefruit juice 250 ml contains Carbohydrate Sugar Protein 19.5 g | 16.5 g | 1.5 g

Answers
Answer:
13.2 g
Step-by-step explanation:
let x = grams sugar in a 200 ml glass
16.5 g sugar / 250 ml = x g sugar / 200 ml
x(250) = (16.5)(200)
x = (16.5)(200) / (250) = 3300 / 250 = 13.2
Answer: there are 13.2 g sugar in a 200 ml glass of juice
help me and ill give you brainliest thanks

Answers
What is an equation in point-slope form of the line shown in the graph, using the point (1, 5)?
Answers
Answer:
The point-slope form is
y
+
6
=
1
5
(
x
−
4
)
or
y
+
5
=
1
5
(
x
−
9
)
, depending on which point you use. If you solve for
y
to get the slope-intercept form, both equations will convert to
y
=
1
5
x
−
34
5
Step-by-step explanation:
6) Brad's father asked an engineer to survey the field behind their house. He wanted to plant some orange and tangerine trees there. According to the survey, the field is thirty metres long and twenty-six metres wide. What is the perimeter of the field in kilometres?
Answers
Answer:
the perimeter of the field in kilometers is 112 km
Step-by-step explanation:
The computation of the perimeter of the field in km is shown below:
As we know that
Perimeter is
= 2(length + width)
= 2(30 + 26)
= 2 (56)
= 112 km
Hence, the perimeter of the field in kilometers is 112 km
How do you find the inverse of a 3 matrix?
Answers
Answer:
Inverse of a 3 by 3 Matrix
MM-1 = M-1 M = I.
Step 1: The first step while finding the inverse matrix is to check whether the given matrix is invertible. ...
Step 2: Calculate the determinant of 2 × 2 minor matrices.
Step 3: Formulate the cofactor matrix.
Step-by-step explanation:
The inverse matrix formula, A-¹ = (1/|A|) Adj A, is used to determine the inverse of a 3×3 matrix.
What is Inverse of Matrix ?The multiplicative identity is obtained by multiplying the provided matrix by the other matrix which serves as the inverse of a matrix. A matrix's inverse is A-1, since the I is the identity matrix, A A-1 = A-1 A = I.
How can I determine the 3X3 Matrix's inverse?The formula A-1 = (adj A)/(det A), where det A is in the denominator, is used to determine the inverse of a 3x3 matrix A.
• adj A = The adjoint matrix of A
• det A = determinant of A
dAs a result, det A should not be 0 for A-1 to exist. i.e.,
• A-1 exists when det A ≠ 0 (i.e., when A is nonsingular)
• A-1 does not exist when det A = 0 (i.e., when A is singular).
To know more about inverse matrix :
https://brainly.com/question/4017205
#SPJ4
Estimate the product. Then find the exact product.
7.9(10.1)
1)estimated product = 80, exact product = 7.97
2)estimated product = 80, exact product = 79.79
3)estimated product = 80, exact product = 797
4)estimated product = 80, exact product = 7,979
Answers
Answer:
estimated product = 80, exact product = 79.79
Step-by-step explanation:
Trust me
Answer:
its 79.79
Step-by-step explanation:
if m=-2,then what is n in this equation

Answers
Answer:
n=-1
Step-by-step explanation:
Plug in m=-2 into the given equation and solve
5(-2 - n) =5n
Distribute the 5 to the -2 and -n
-10-5n=5n
Isolate the variable to one side by adding 5n to the right side of the equation.
-10=10n
Isolate the variable by dividing by 10 on both sides.
-1 = n
The ratios of corresponding sides in the two triangles
are equal.
What other information is needed to prove that AFGE
- AIJH by the SAS similarity theorem?
PLEAS HELP?
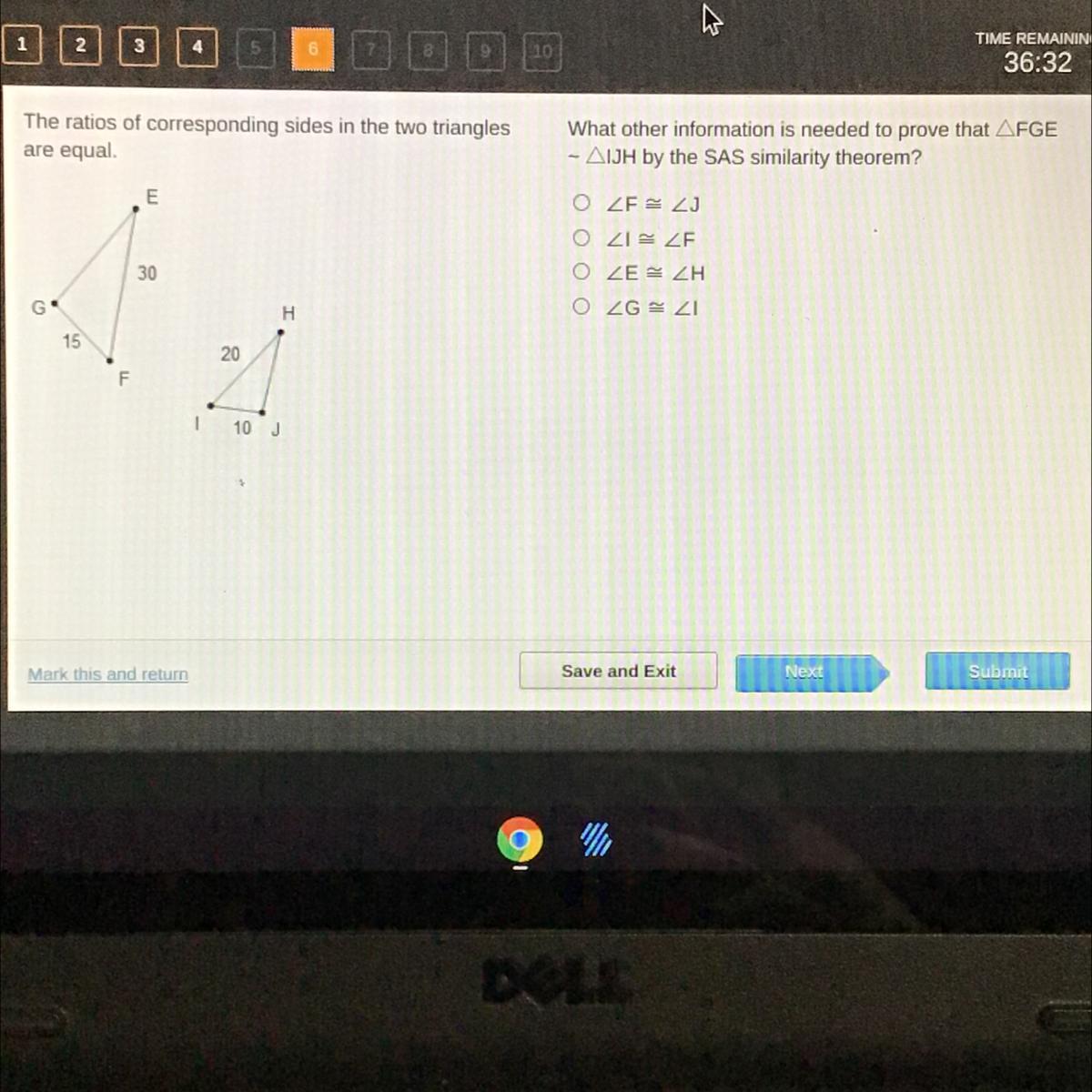
Answers
Answer:
2nd Choice
Step-by-step explanation:
because in SAS, we use 2 sides and the angle between them
The part used to prove the triangles are similar using SAS similarity is
<I = <F.
What is Similarity?If the proportion of the two sides of one triangle is the same as the proportion of the two sides of another triangle, and the angle inscribed by the two sides of both triangles is equal, two triangles are said to be similar.
The three-sided polygon is the triangle. The following is the criteria for triangle similarity:
Corresponding angles of both triangles are equal, corresponding sides of both triangles are proportional to each other.To prove for SAS similarity, we need ratio of two corresponding sides of two triangles equal.
and, one angle which is in between the sides used for ratio.
As, ratios of corresponding sides in the two triangles are equal.
FG / IJ = GE / JH = EF / IH
So, the angle will be <I = <F.
Learn more about Similarity here:
https://brainly.com/question/26451866
#SPJ7
Type the integer that makes the following division sentence true: 50 –250
Answers
The integer that makes the sentence true is -200
How to determine the integerFrom the question, we have the following parameters that can be used in our computation:
50 - 250
The above expression is not a division sentence
Instead, it is a subtraction sentence
using the above as a guide, we have the following:
50 - 250
Evaluate the difference in the sentence above
50 - 250 = -200
Hence, the integer is -200
Read more about expression at
https://brainly.com/question/4344214
#SPJ1
a student has to sell 2 books from a collection of 6 math, 7 science, and 4 economics books. how many choices are possible if both books are to be on the same subject? the books are to be on different subjects?
Answers
There are 78 possible choices if both books are on the same subject, and 168 possible choices if the books are on different subjects.
1. Same subject: To find the number of choices when both books are on the same subject, we can calculate the combinations of selecting 2 books from each subject category and sum them up. There are 6 math books, so the number of combinations is C(6, 2) = 15. Similarly, for science books, there are C(7, 2) = 21 combinations, and for economics books, there are C(4, 2) = 6 combinations. Adding them up, we get 15 + 21 + 6 = 42 combinations.
2. Different subjects: To find the number of choices when the books are on different subjects, we need to calculate the combinations of selecting 1 book from each of the three subject categories and multiply them. There are 6 math books to choose from, 7 science books, and 4 economics books. So the total number of combinations is 6 * 7 * 4 = 168.
Learn more about multiply : brainly.com/question/620034
#SPJ11
Mrs Ross runs a tutoring business she charges $35 an hour plus a $50 application fee her competitor Mrs brand charges $45 an hour plus $25 application fee right an equation that represent the situation when the cost to be tuned by Mrs Ross and Mr brand is the same
Answers
Each of the sides of a pentagon is 12 cm long. Two ants are walking from point A to point D along the sides of the pentagon. One ant walks from point A to point B to point C to point D at an average speed of 3 centimeters per second. The other ant walks from point A to point E to point D, arriving at point D at the same time as the first ant. What is the average speed of the second ant, in cm per second?
Answers
Answer:
The average speed of the second ant is 2 cm/s
Step-by-step explanation:
The details of the ants moving on the sides of the pentagon are;
The length of the sides of the pentagon = 12 cm
The path of the first ant = A to B, B to C, then C to D
The average speed of the first ant = 3 cm/s
The path of the second ant = A to E, and E to D
The time of arrival of the second ant at the point D = The time of arrival of the first ant at the point D
Given that both ants departed at the same time, from point A, we have;
The time it takes the first ant to arrive at the point D = The time it took the second ant to arrive at the point D
The distance from A to B = 12 cm
The distance from B to C = 12 cm
The distance from C to D = 12 cm
∴ The distance traveled by the first ant from A to D = 12 cm + 12 cm 12 cm = 36 cm
Average speed = (Total distance)/(Total Time)
Total time = (Total distance)/(Average speed)
Let 't' represent the time it takes the first ant to move from point A to point D, we have;
t = 36 cm/(3 cm/s) = 12 seconds
Therefore, the time it takes the first ant to move from point A to point D, t = 12 seconds = The time it takes the second ant to move from point A to point D through point E
The total distance traveled by the second ant from A to point E, then from point E to point D, \(T_{d2}\) = 12 cm + 12 cm = 24 cm
The average speed of the second ant, v₂ = \(T_{d2}\)/t
∴ v₂ = 24 cm/(12 seconds) = 2 cm/s
The average speed of the second ant, v₂ = 2 cm/s.
Find the area. Round your answer to the
nearest tenth.
1.
3.
3 m
18 in.
2.
4.
25 ft
(Just the two bottom ones)

Answers
a) The area of the first circle is approximately 254.34 square inches
b) The area of the second circle is approximately 70650 square inches.
a) The area of a circle can be calculated using the formula A = πr², where π (pi) is a mathematical constant approximately equal to 3.14, and r is the radius of the circle.
For the first circle with a diameter of 18 inches, we can find the radius by dividing the diameter by 2:
r = 18/2 = 9 inches
Now we can calculate the area using the formula:
A = πr² = 3.14 x 9² = 254.34 square inches
Therefore, the area of the first circle is approximately 254.34 square inches.
b) For the second circle with a diameter of 25 feet, we need to convert the diameter to inches, since our formula uses radius in inches:
25 feet = 25 x 12 inches = 300 inches
Then we can find the radius by dividing by 2:
r = 300/2 = 150 inches
Now we can calculate the area using the formula:
A = πr² = 3.14 x 150² = 70650 square inches
Therefore, the area of the second circle is approximately 70650 square inches.
Note that the units for the second calculation are in square inches, not square feet, because we used the formula that requires radius in inches.
To learn more about area click on,
https://brainly.com/question/16599566
#SPJ1
6. There are only cars and trucks in the parking lot. Five out of every 13
vehicles are cars. If there are 143 vehicles in the parking lot, how many
are trucks?
Pls help me
Answers
Answer:
88 trucks
Step-by-step explanation:
Ratio of cars : vehicles = 5:13
Hence, the ratio of trucks : vehicles = 8:13
143/13 = 11
If the number of vehicles is 143,
we have to multiply both sides of the ratio by 11:
8*11 : 13* 11
88 : 143
Hence, there are 88 trucks for every 143 vehicles.
Hope this answers your question... Have a wonderful time ahead at Brainly!
Sorry, ignore the other question I had on here, that was a typo. How do you find the positive/negative intervals of f(x) = 3/(x + 5) ? Please show in full detail!!
Answers
Answer:
Positive interval: x is in (-5, infty)
Negative interval: x is in (-infty, -5)
Step-by-step explanation:
A fraction is positive when the numerator and denominator have the same sign. Since the numerator is positive in this case, the fraction will be positive when it's denominator is also positive. Thus, we need to solve x+5>0. Subtracting 5 on both sides gives x>-5.
Positive interval: x is in (-5, infty)
A fraction is is negative when the numerator and denominator have the different signs. Since the numerator is positive in this case, the fraction will be negative when it's denominator is negative. Thus, we need to solve x+5<0. Subtracting 5 on both sides gives x<-5.
Negative interval: x is in (-infty, -5)
A fraction doesn't have an output when it's denominator is 0. That is, in this case when x+5=0 which is when x is -5.