Answers
Answer:
16
Step-by-step explanation:
A____(6)_____B____(10)_____C
6+10=16
Hope this helps!
Related Questions
"
Solve the initial value problem. {d y}/{d t}=5 t sin ^{2} y, y(1)={3 \pi}{4} The solution is
"
Answers
The solution to the initial value problem dy/dt = 5t sin^2(y) with y(1) = 3π/4 is given by y = (5/2)t^2 - π/4 - (5/2).
To solve the initial value problem dy/dt = 5t sin^2(y) with the initial condition y(1) = 3π/4, we can separate variables and then integrate both sides.
Step 1: Separate variables
dy/sin^2(y) = 5t dt
Step 2: Integrate both sides
∫dy/sin^2(y) = ∫5t dt
To integrate the left side, we can use a trigonometric identity. Let's rewrite sin^2(y) as (1 - cos^2(y)):
∫dy/(1 - cos^2(y)) = ∫5t dt
Now, let's use the identity sec^2(y) = 1 + tan^2(y) to further simplify the integral:
∫dy/(1 + tan^2(y)) = ∫5t dt
The integral on the left side is now in a form that can be evaluated easily. It is equal to arctan(tan(y)):
arctan(tan(y)) = (5/2)t^2 + C
Step 3: Solve for y
Since y(1) = 3π/4, we can substitute this value into the equation:
arctan(tan(3π/4)) = (5/2)(1)^2 + C
arctan(-1) = (5/2) + C
Now, we can solve for C:
C = arctan(-1) - (5/2)
C = -π/4 - (5/2)
Step 4: Substitute C back into the equation
Now we can substitute the value of C back into the equation to find the solution:
arctan(tan(y)) = (5/2)t^2 - π/4 - (5/2)
Since arctan(tan(y)) is equal to y, we have:
y = (5/2)t^2 - π/4 - (5/2)
Learn more about variables at: brainly.com/question/15078630
#SPJ11
Solve the initial value problem. {d y}/{d t}=5 t sin ^{2} y, y(1)={3 \pi}{4} What is the solution?
Find the horizontal asymptote of the function .
y =
Answers
Answer:
the graph of an exponential function f(x) = bx approaches , but does not cross the x-axis.
the x-axis is a horizontal asymptote
Alyssa’s extended family is staying at the lake house this weekend for a family reunion. She is in charge of making homemade pancakes for the entire group. The pancake mix requires 2 cups of flour for every 10 pancakes.
1. Write a ratio to show the relationship between the number of cups of flour and the number of pancakes made.
2. Determine the value of the ratio.
3. Use the value of the ratio to fill in the following two multiplicative comparison statements.
a. The number of pancakes made is ________ times the amount of cups of flour needed.
b. The amount of cups of flour needed is ________ of the number of pancakes made.
4. If Alyssa has to make 70 pancakes, how many cups of flour will she have to use?
Answers
Answer:
1. 2:10 or 1:5
2. 20%
3a. 5
3b. 1/5
4. 14 cups. If you multiply the ratio by 7 to get 70 total pancakes, the other value will be 14.
2:10 * 7 = 14:70
HELPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPP
Kayla wants to find 223 ÷ (-137). She first rewrites the division as (223) (-173).
What is wrong with Kayla’s reasoning?
Answers
Answer:
Kayla ended up multiplying instead of dividing
Step-by-step explanation:
If Kayla works out (223) (-173) She will end up multiplying since she didn't include the division symbol.
With a coupon, you can get a pair of shoes that normally costs $85 for only $68. What percentage was the discount?
Answers
Answer:
20 percent
Step-by-step explanation:
Im too late but for the dub
write an equation
85x=68
Divide 85 on both sides
x=0.8
0.8=80%
100-80=20
so 20% discount.
Josh pulled cards from a deck 200 times. He pulled a red card 120 times and a black card 80 times. What is the experimental probability that the next card is black? Remember to simplify.
Answers
Look at the picture and thanks

Answers
Answer:
E
Step-by-step explanation:
Sjsjdjddjdjdjjddjdjdjdjdjdndnsnsnsbs answer is E
Answer: C i think
Step-by-step explanation: hop this helps :)
Evaluate if a = - 3 and b = 2
-3a/B^2
Answers
Answer:
9/4
Step-by-step explanation:
= -3a
= -3(-3)
= 9
=B^2
= (2)^2
=4
therefore answer: 9/4
A hollow copper wire with an inner diameter of 1.1 mm and an outer diameter of 2.3 mm carries a current of 12 A. What is the current density in the wire?
Answers
The current density in the wire is 3.75 A/mm^2.
The current density (J) is defined as the current per unit area of cross-section perpendicular to the direction of current flow. It can be calculated using the formula:
J = I / A
where I is the current flowing through the wire and A is the cross-sectional area of the wire.
To find the cross-sectional area of the wire, we need to subtract the area of the inner circle from the area of the outer circle. The area of a circle is given by the formula:
A = πr^2
where r is the radius of the circle.
The radius of the inner circle is 0.55 mm (1.1 mm / 2), and the radius of the outer circle is 1.15 mm (2.3 mm / 2).
The area of the inner circle is:
π(0.55 mm)^2 = 0.95 mm^2
The area of the outer circle is:
π(1.15 mm)^2 = 4.15 mm^2
The cross-sectional area of the wire is the difference between these two areas:
A = 4.15 mm^2 - 0.95 mm^2 = 3.2 mm^2
Now we can calculate the current density:
J = I / A = 12 A / 3.2 mm^2 = 3.75 A/mm^2
Therefore, the current density in the wire is 3.75 A/mm^2.
Click the below link, to learn more about current density:
https://brainly.com/question/989514
#SPJ11
PLEASE ANSWER ASAP TY
In triangle ABC below, BD is the altitude. Find the length of DC. Leave your answer in
simplified radical form.

Answers
Answer:
Step-by-step explanation:
Step 1: Find AB Use Pythagoras Theorem
AB = \(\sqrt{AC^{2} -BC^{2} } = \sqrt{12^{2} -8^{2} } = \sqrt{80}\)
Step 2: Find the Area of the triangle ABC
Area = \(\frac{1}{2}AB.BC = \frac{1}{2}\sqrt{80}.8 = 4\sqrt{80}\) = \(16\sqrt{5}\)
Step 3: Find BD. Use the area of the triangle above
Area = \(\frac{1}{2}BD.AC\)
We already known the Area and AC so, we just plug all the number in
BD = \(\frac{2. Area}{AC}\) = \(\frac{2.16\sqrt{5}}{12}\) = \(\frac{8\sqrt{5}}{3}\)
Step 4: Find DC. Use Pythagoras Theorem of the triangle BDC
DC = \(\sqrt{BC^{2}-BD^{2} }\) = \(\sqrt{8^{2}-(\frac{8\sqrt{5}}{3})^{2}}\) = \(\frac{16}{3}\)
Please help solve this equation. Equation is below. Thank you!

Answers
First, you should try to find 2 equations where there are only two variables. So, I cancelled out the z variable and made 2 equations that only included x and y.
Then, I used a system of equations again to solve for y, then I plugged in y to find x.
Then, finally you can plug in x and y into one of the original equations to find z.
All my steps are in the photo, if you have any other questions let me know!

Please help with this geometry question too.

Answers
Answer:
V = 1250π/3 mm³
V = 1309 mm³
Step-by-step explanation:
The composite figure is made up of a cylinder with radius 5 mm and two hemispheres of radius 5 mm. The height of the cylinder is
20 mm - 5 mm - 5 mm = 10 mm
The two hemispheres make up a full sphere of radius 5 mm.
V = πr²h + (4/3)πr³
V = π(5 mm)²(10 mm) + (4/3)π(5 mm)³
V = [(25 mm²)(10 mm) + (4/3)(125 mm)³]π
V = [250 mm³ + 500/3 mm³]π
V = 1250π/3 mm³
V = 1309 mm³
PLEASE HELP! find the sum. express your answer in simplest form. (6g - 6) / (h^2 - 5) + (-g + 7) / (h^2 - 5)
Answers
Answer:
\(\frac{5g+1}{h^2-5}\)
Step-by-step explanation:
\(\frac{6g-6}{h^2-5}\) + \(\frac{-g+7}{h^2-5}\)
Since the fractions have a common denominator of h² - 5 , then add the numerators over the common denominator
= \(\frac{6g-6-g+7}{h^2-5}\)
= \(\frac{5g+1}{h^2-5}\)
agency (epa) releases fuel economy data on cars manufactured in that year. below are summary statistics on fuel efficiency (in miles/gallon) from random samples of cars with manual and automatic transmissions. do these data provide strong evidence of a difference between the average fuel efficiency of cars with manual and automatic transmissions in terms of their average city mileage? assume that conditions for inference are satisfied
Answers
No, the data does not provide strong evidence of a difference between the average fuel efficiency of cars with manual and automatic transmissions in terms of their average city mileage.
A hypothesis test should be performed to determine whether there is strong evidence that the average fuel efficiency of manual and automatic transmission vehicles differs in relation to average city mileage.
Let μm be the true population average urban mileage for manual transmission vehicles and μa be the true population average urban mileage for automatic transmission vehicles.
Tests whether the means of two populations are significantly different.
The null and alternative hypotheses can be set as follows.
Null Hypothesis (H0):
µm - µa = 0
Alternative hypothesis (Ha):
µm - µa ≠ 0
A two-sample t-test can be used to test this hypothesis. We can assume that the conditions for inference are met, including independence, normality, and equal variances between the two groups.
The test statistic can be computed as
\(t = (xm - xa) / (s^2p * (1/nm + 1/na))^0.5\)
where xm and xa are the sample means of urban kilometers for manual and automatic transmission vehicles, nm and na are the sample sizes of the two groups, \(sp^2\) is the pooled variance, and\(s^2p\)is the pooled standard deviation.
A significance level of α = 0.05 can be used for the test.
If the calculated t-value is greater than the critical t-value from the t-distribution with degrees of freedom (nm + na - 2) and significance level α/2 = 0.025, we reject the null hypothesis and conclude that can do.
There is a clear difference between the average fuel efficiency of manual and automatic vehicles in relation to average city mileage.
If the calculated t-value is less than the critical t-value, then the null hypothesis is not rejected and the conclusion is that there is insufficient evidence to support the difference between the two population means.
You can't run tests and draw conclusions without seeing the actual summary statistics.
learn more about Null Hypothesis
brainly.com/question/28920252
#SPJ4
Which of the following sets is not finite?

Answers
Because if you do that by there you can do that
Use prime factorisation to work out the square root 9604.
Answers
Answer:
98
Step-by-step explanation:
To find the square root of 9604 using prime factorization we have to rewrite the number 9604 using a multiplication of prime factors.
Take the prime numbers in order from least towards greatest 2,3,5,7,11,13,...and check if they divide evenly with our number 9604.
→If the number ends in an even number is divisible by 2
is 9604 divisible by 2? yes so do
9604 /2 = 4802
is 4802 divisible by 2? yes so do
4802/2 = 2401
is 2401 divisible by 2? no so check the divisibility by 3 (second prime number)
→If the sum of all digits is a multiple of 3 the number is divisible by 3
is 2401 divisible by 3?
2+4+0+1 = 7 is not a multiple of 3 so no, so check divisibility by 5
→If the number ends in 0 or 5 is divisible by 5
is 2401 divisible by 5? no so check divisibility by 7
→If the difference of the number without the last digit and double of the last digit is a multiple of 7 then the number is divisible by 7
is 2401 divisible by 7
240- 2*1 = 240 -2 = 238
23-2*8 = 23-16 = 7 so yes the number 2401 is divisible by 7
2401/7 = 343
is 343 divisible by 7 yes because 34-2*3= 34-6 = 28 is a multiple of 7
343/7 =49
is 49 divisible by 7 yes
49/7 = 7
is 7 divisible by 7 yes
7/7 = 1
The number 9604 can be written as
9604 = 2*2* 7*7*7*7
The square root 9604 is
√9604 = √2*2*7*7*7*7 = 2*7*7 = 98

can someone pls help? i've been waiting over an hour

Answers
Answer:
22
Step-by-step explanation:
5(7)=35
3(8)=24
35-24+11=22
Answer:
22
Step-by-step explanation:
\(5c - 3d + 11\\\rule{150}{0.5}\\5(7)-3(8)+11\\\\35 - 24 + 11\\\\11 + 11\\\\\boxed{22}\)
Hope this helps!
Which is the area between the x-axis and y=x^2 from x=2 to x=6
Answers
For this problem, we need to use our integral knowledge to set up the problem:
The bounds will be from 2 to 6, cutting tiny horizontal bars into the graph, to approximate the area
Now for the function inside the integral:
⇒ it is the top function minus the bottom function
top function: y= x²bottom function: x-axis ⇒ y =0⇒ function within integral = x² - 0
Let's put it all together and solve:
\(Area=\int\limits^6_2 {x^2-0} \, dx =\int\limits^6_2 {x^2} \, dx=\frac{6^3}{3} -\frac{2^3}{3} \\Area=\frac{6^3-2^3}{3} =\frac{216-8}{3} =\frac{208}{3}\)
Answer: 208/3 ≈ 69.333
Hope that helps!
Please solve, -8-2(7r+1)=-94
Answers
Answer:
r = 6
Step-by-step explanation:
Hello!
-8 - 2(7r + 1) = -94
Add 8 to both sides
-2(7r + 1) = -86
Divide both sides by -2
7r + 1 = 43
Subtract 1 from both sides
7r = 42
Divide both sides by 7
r = 6
Hope this Helps
-10-14r=-94
-14r=-84
r=6
13.10 − Let Mn be the maximum of n independent U(0,1) random variables. a. Derive the exact expression for P(∣Mn−1∣>ε). Hint: see Section 8.4. b. Show that limn→[infinity]P(∣Mn−1∣>ε)=0. Can this be derived from Chebyshev's inequality or the law of large numbers?
Answers
This can be derived using Chebyshev's inequality, as Chebyshev's inequality and the law of large numbers are different in nature.
Let M_n be the maximum of n independent U(0, 1) random variables.
To derive the exact expression for P(|M_n − 1| > ε), we need to follow the below steps:
First, we determine P(M_n ≤ 1-ε). The probability that all of the n variables are less than 1-ε is (1-ε)^n
So, P(M_n ≤ 1-ε) = (1-ε)^n
Similarly, we determine P(M_n ≥ 1+ε), which is equal to the probability that all the n variables are greater than 1+\epsilon
Hence, P(M_n ≥ 1+ε) = (1-ε)^n
Now we can write P(|M_n-1|>ε)=1-P(M_n≤1-ε)-P(M_n≥1+ε)
P(|M_n-1|>ε) = 1 - (1-ε)^n - (1+ε)^n.
Thus we have derived the exact expression for P(|M_n − 1| > ε) as P(|M_n-1|>ε) = 1 - (1-ε)^n - (1+ε)^n
Now, to show that $lim_{n\to\∞}$ P(|M_n - 1| > ε) = 0 , we can use Chebyshev's inequality which states that P(|X-\mu|>ε)≤{Var(X)/ε^2}
Chebyshev's inequality and the law of large numbers are different in nature as Chebyshev's inequality gives the upper bound for the probability of deviation of a random variable from its expected value. On the other hand, the law of large numbers provides information about how the sample mean approaches the population mean as the sample size increases.
Learn more about Chebyshev's inequality:
https://brainly.com/question/32750368
#SPJ11
#1. What is the angle of elevation to the lighthouse? Round to the nearestdegree.

Answers
Since the situation forms a right angle we can apply trigonometric functions:
Sin a = opposite side / hypotenuse
Where:
a = angle = x
opposite side = 168
hypotenuse = 360
Replacing:
Sin x = 168/360
Solve for x
x = Arc sin (168/360)
x = 27.81 = 28 °
Please answer!! Screenshot attached
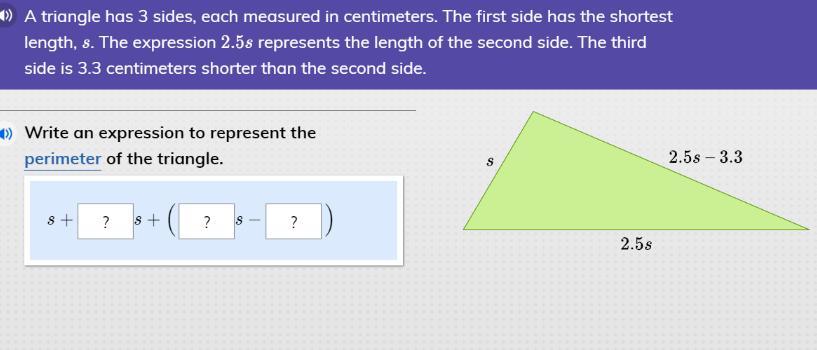
Answers
Answer:
there is a website where you can make triangles and that would get it 4 u
Step-by-step explanation:
At the last cinema showing, 245 tickets were sold. An adult ticket costs $8 and a child ticket costs $5. Determine how many children and adults attended the last session if the revenue was $1768?
(I have the answer already)
(this a test for you)
Answers
Let's represent the number of adult tickets sold as "x" and the number of child tickets sold as "y".
We know that a single adult ticket costs $8, so the total revenue from adult ticket sales would be 8x. Similarly, a single child ticket costs $5, so the total revenue from child ticket sales would be 5y.
The total number of tickets sold was 245, so we can write an equation:
x + y = 245
We also know that the total revenue was $1768:
8x + 5y = 1768
We can use the first equation to solve for one of the variables in terms of the other:
y = 245 - x
Substitute this into the second equation:
8x + 5(245 - x) = 1768
Simplify and solve for x:
8x + 1225 - 5x = 1768
3x = 543
x = 181
So 181 adult tickets were sold. We can use the first equation to find the number of child tickets:
181 + y = 245
y = 64
So 64 child tickets were sold.
Express the proposition, the converse of p→q, in an English sentence, and determine whether it is true or false, where p and q are the following propositions.
p:"77 is prime" q:"77 is odd"
Answers
The converse of p→q, "If 77 is odd, then 77 is prime," is a false statement.
The proposition p→q, in English, is "If 77 is prime, then 77 is odd." The converse of p→q is q→p, which can be expressed as "If 77 is odd, then 77 is prime."
To determine whether this converse is true or false, let's first examine the truth values of the propositions p and q:
p: "77 is prime" - This statement is false, as 77 is not prime (it has factors 1, 7, 11, and 77).
q: "77 is odd" - This statement is true, as 77 is not divisible by 2.
Now, let's evaluate the truth value of the converse q→p:
q→p: "If 77 is odd, then 77 is prime" - Since the premise (q) is true and the conclusion (p) is false, the overall statement q→p is false. A conditional statement is only true when the premise being true leads to the conclusion being true. In this case, the fact that 77 is odd does not imply that it is prime.
To know more about conditional statement, refer to the link below:
https://brainly.com/question/10714086#
#SPJ11
The picturegram shows information about CDs sold in a shop.
1 . How manny CDs were sold on Wednesday | Key = 3 |
2. How manny more CDs were sold on Thursday than Wednesday?
**If you know the answer let me know!**

Answers
Answer:
i believe number 1 is 18 and number 2 is 9.
Step-by-step explanation:
if one full circle represents 6 CDs then on wednesday 18 Cds were sold because 6+6+6=18 and on thursday they sold 9 more Cds than on wednesday because they sold 6+6+6+6+3 which equals 9.
Factor completely 4x^2 - 4x - 8
Answers
Answer:
4(x+1) x (x-2)
Step-by-step explanation:
Hi! Let me help you! :)
Remember, factoring looks like so:ab+ac=a(b+c)In this case, a is the common term, so we factor it out.Now, let's check our polynomial and see if we can spot the common term.All terms are divisible by 4, so 4 is the common term.4x²-4x-8x²-x-2Answer:
x²-x-2
Hope you find it helpful.
\(\rm{Stargazing{\bold{WithJoy!} :D\)
What kind and how much polygons do you see in the net of the triangular prism?
Answers
The net of a triangular prism consists of two triangles and three rectangles.
In the net of a triangular prism, we can observe two types of polygons: triangles and rectangles.
First, let's discuss the triangles.
A triangular prism has two triangular faces, which are congruent to each other.
These triangles are equilateral triangles, meaning they have three equal sides and three equal angles.
Each of these triangles contributes two polygons to the net, one for each face.
Next, we have the rectangles.
A triangular prism has three rectangular faces that connect the corresponding sides of the triangular bases.
These rectangles have opposite sides that are parallel and equal in length.
Each rectangle contributes one polygon to the net, resulting in a total of three rectangles.
To summarize, the net of a triangular prism consists of two equilateral triangles and three rectangles.
The triangles represent the bases of the prism, while the rectangles form the lateral faces connecting the bases.
Altogether, there are five polygons in the net of a triangular prism.
It's important to note that the dimensions of the polygons may vary depending on the specific size and proportions of the triangular prism, but the basic shape and number of polygons remain the same.
For similar question on triangular prism.
https://brainly.com/question/31303784
#SPJ8
The radius of a ball was measured and found to be 25 cm with a possible error in measurement of at most 0.01cm. What is the maximum error in using this value of the radius to compute the volume of the ball
Answers
Answer:
25 x 0.01
Step-by-step explanation:
here you go . ..........................................
What is the distance between 0 and 4 on the number line? ? units -5 -4 -3 -2 -1 0 2 3 4 5
Answers
Answer:
4 - 0 = 4
Step-by-step explanation:
The distance is 4 units from 0 to 4
the distance lesley walks from home to school is 120 meters and 80 meters when he goes to church from home. gusion estimates that the distance lesley walks when he goes directly to church. coming frim school is 180 meters. guinevere's estimation is 210 meters which etimation is feasible? make a map of lesley ways from home to school and church justify.
Answers
Guinevere’s estimation of 210m is not feasible.
Gusion’s estimate is feasible if the locations form a triangle.
