Answers
Answer:
here's the link to the answer
Step-by-step explanation:
WWW.math.com/int.etg
Related Questions
Use the function g(x)=11 to find the following values g(-3), g(5), g(a), g(a+h)
Answers
The evaluated function values are g(-3) = 11, g(5) = 11, g(a) = 11 and g(a+h) = 11
Evaluating the function valuesA composite function is a function that results from combining two or more functions. It is created by using the output of one function as the input of another function.
The function g(x) is defined as g(x) = 11, which means that the output of the function is always 11, no matter what value of x is inputted.
i.e. the function g(x) = 11 always returns the value 11, regardless of the input.
Therefore, we have:
g(-3) = 11
g(5) = 11
g(a) = 11
g(a+h) = 11
So, regardless of the value of a or h, the function g(x) will always return 11.
Read more about function at
https://brainly.com/question/28532394
#SPJ1
Someone help quickly pls :(
Assignment
Practice finding solutions to systems of equations using
substitution.
The value of x in this system of equations is 1.
3x + y = 9
y=-4x+10
1. Substitute the value of y in the first equation:
2. Combine like terms:
3. Apply the subtraction property of equality:
4. Apply the division property of equality:
What is the value of y?
y=
3x + (-4x+10) = 9
-x+10=9
-x=-1
x=1
Answers
Answer:
y = 6
Step-by-step explanation:
Solving system of linear equation using substitution method:3x + y = 9 ---------------(I)
y = -4x + 10 -----------------(II)
Substitute y = -4x + 10 in equation (I)
3x - 4x + 10 = 9
Combine like terms,
-x + 10 = 9
Subtract 10 from both sides. (subtraction property of equality)
-x = 9 - 10
-x = -1
Divide both sides by (-1). {Division property of equality}
\(\sf \dfrac{-x}{-1}=\dfrac{-1}{-1}\\\\ \boxed{x = 1}\)
Now, substitute x = 1 in equation (II) and find the value of y.
y = -4*1 + 10
= -4 + 10
\(\sf \boxed{\bf y = 6}\)
HOW MANY TIMES DOES 9 DIRECTLY PRECEDE 2 IN THIS SEQUENCE: 12909296292629
Answers
9 directly precede 2, 4 times, in the sequence, 12909296292629.
What is a sequence?An ordered list of things is a sequence (or events). Similar to a set, it has members (also called elements, or terms). The length of the sequence is the number of ordered items (potentially infinite).
In the given sequence,
12909296292629,
there are 4 such 9's that are preceded by 2 immediately.
That means, for the clear representation,
1-29-09-29-6-29-26-29
Therefore, there are 4 such 9's that are preceded by 2.
To learn more about the sequence;
https://brainly.com/question/21961097
#SPJ1
Watch help video
What is the equation of the line that passes through the point (8, 3) and has a slope
of -1?
Answers
Answer:
y = -x + 11
Step-by-step explanation:
y = mx + b
m is the slope and b is the y-intercept so m = -1
y = -x + b
Now substitute x = 8 and y = 3:
3 = -8 + b
b = 11
Thus the final equation is y = -x + 11.
class limits and class boundaries please

Answers
The class limit of the given data is the actual values from the data that represents the lower values and the larger values of a data set. While the class boundaries represents the values that eliminate gaps between the classes in the frequency distribution which are one decimal place more accurate than the data.
How to determine the class boundary and class limit of the given data above?To determine the class limit, using a class interval of 5.00, the following should be carried out;
The lowest figure from the given data set = 48.6. Therefore, the lower class interval should start from a figure lower than 48.6 such as = 45.0
For the class limits;
= 46.0 - 50.0
50.0 - 54.0
54.0 - 58.0
58.0 - 62.0
62.0 - 66.0
66.0 - 70.0
70.0 - 74.0
74.0 - 78.0
78.0 - 82.0
82.0 - 86.0
86.0 - 90.0
90.0 - 94.0
The class boundaries would be determined below:
45.50 - 50.50
50.50 - 54.50
54.50 - 58.50
58.50 - 62.50
62.50 - 66.50
66.50 - 70.50
70.50 - 74.50
74.50 - 78.50
78.50 - 82.50
82.50 - 86.50
86.50 - 90.50
90.50 - 94.50
94.50 - 99.50
Learn about class limits here:
https://brainly.com/question/30267084
#SPJ1
Rationalize the numerator
\(\frac{\sqrt{3} -5}{\sqrt{2} +5 }\)
(Simplify your answer. Type an exact answer, using radicals as needed.)
Answers
The surd is rationalized to give √6 - 5√3 + 5√2 - 25/2 + 25
How to rationalize the fractionIt is important to note that fractions are a part of whole number or element.
The different types of fraction includes;
Simple fractionsComplex fractionsProper fractionsImproper fractions, etcGiven the expression;
√3 - 5/√2 + 5
√3 - 5/ √2 + 5 ×√2 - 5/√2 - 5
Multiply the values
√6 - 5√3 + 5√2 - 25/√4 - 5√2 + 5√2 + 25
Add the like surds and find the square roots, we get
√6 - 5√3 + 5√2 - 25/2 + 25
Hence, the expression is √6 - 5√3 + 5√2 - 25/2 + 25
Learn about surds on:
https://brainly.com/question/840021
#SPJ1
Answer For Brainiest!
What 3D Objects' do EACH Net Make?




Answers
Looking at the 4th net, we see it has what seems to be 4 squares in a line. And two of them are each one united into another square.
Then, when we join the left side of the left square and the right side of the right square, we obtain a 3D object with 4 square faces, and 2 empty faces also in the form of a square.
After that, we can fold down the upper square face, and fold up the other one.
We will get the following 3D object, that is a cube:
Therefore, the 4th net makes a cube.

HELP ME OUUTT THANKS
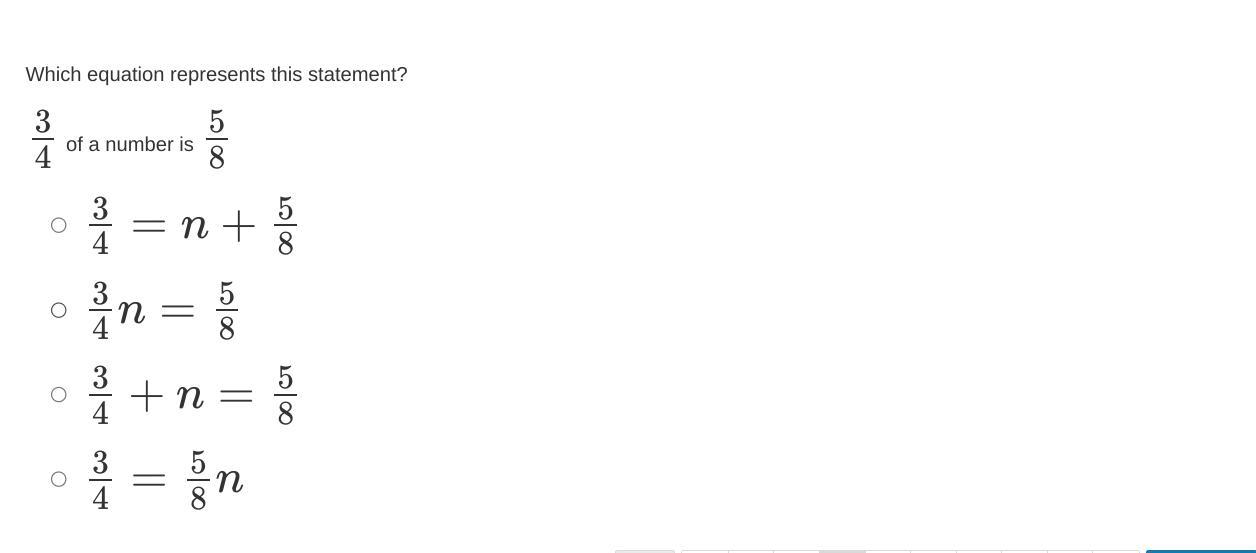
Answers
Answer:
3/4n = 5/8
Step-by-step explanation:
your…. welcome……
I don’t trust meself so I might be wrong
Graph the data, and find the slope and y-intercept from the graph.
Then write an equation for the graph in slope-intercept form.

Answers
A graph of the data is shown in the image attached below.
The slope is equal to 0.4.
The y-intercept from the graph is equal to
An equation for the graph in slope-intercept form is y = 0.4x + 2.
How to calculate the slope of a line?Mathematically, the slope of a straight line can be calculated by using this formula;
Slope, m = (Change in y-axis, Δy)/(Change in x-axis, Δx)
Slope, m = (y₂ - y₁)/(x₂ - x₁)
Substituting the given points into the formula, we have;
Slope, m = (10 - 4)/(20 - 5)
Slope, m = 6/15
Slope, m = 2/5 or 0.4
Mathematically, the slope-intercept form of a straight line is given by;
y = mx + c
Where:
x and y are the points.m represents the slope.c represents the intercept.At point (5, 4), an equation in slope-intercept form is given by:
y - y₁ = m(x - x₁)
y - 4 = 0.4(x - 5)
y - 4 = 0.4x - 2
y = 0.4x - 2 + 4
y = 0.4x + 2.
Read more on slope-intercept form here: brainly.com/question/1884491
#SPJ1

Suppose a network has 37 servers of which 8 fail. How many possibilities are there for the 8 that fail?
Answers
The number of possibilities for 8 of 37 servers to fail is 38608020
How to determine the ways of selection?From the question, we have
Total number of servers, n = 37
Numbers to servers that fail, r = 8
The number of ways for 8 serves to fail is calculated using the following combination formula
Total = ⁿCᵣ
Where
n = 37 and r = 8
Substitute the known values in the above equation
Total = ³⁷C₈
Apply the combination formula
ⁿCᵣ = n!/(n - r)!r!
So, we have
Total = 37!/29!8!
Evaluate
Total = 38608020
Hence, the number of ways is 38608020
Read more about combination at
brainly.com/question/11732255
#SPJ1
Select the expressions that have a value less than -1.
A. -7 ÷ (-4)
B. – (3 ÷ 2)
C. -8/5 x (-5/8)
D. -5/-3
E. (-9) ÷ 6
Answers
Answer:
B and E
Step-by-step explanation:
A. -7 ÷ (-4) = -7/-4 = 7/4 = 1.75
B. -(3 ÷ 2) = -(1.5) = -1.5
C. -8/5 * (-5/8) = (8/5) * (5/8) = 1
D. -5/-3 = 5/3 ≈ 1.667
E. -9 ÷ 6 = -9/6 = -1.5
the last digit in a measured value, whose exact value we cannot know for sure, is referred to as the . multiple choice question. rate-limiting digit certain digit uncertain digit determinant digit
Answers
The "uncertain digit" is the final digit of a measured value whose precise value we are unsure about.
Explain about the uncertain digit?The total number of certain digits in a measurement plus one estimated or uncertain digit make up the significant figures.
Specific graduations or markings on the tool that is used to record the measurement are the basis for some of the digits. A measurement with the more significant figures will be produced by a tool with much more graduations. A guess or estimate of the object's location between the closest graduations is a "uncertain digit." As a result, in a measurement that is accurately reported, the last digit is important but uncertain.Thus, the "uncertain digit" is the final digit of a measured value whose precise value we are unsure about.
To know more about the uncertain digit, here
https://brainly.com/question/1577893
#SPJ4
How to do this problem? Please explain this in steps if possible. Thanks!

Answers
Answer: 10
Step-by-step explanation:
If two triangles are congruent, then they will have the exact same sides and angle measures.
AB=3x+1
BC=6
DE=2x
Solve for X by making 2x=6 because DE and BC are corresponding sides, indicating they are equal.
x=3, plug that in
AB=10
2 Mabaso has R140, Thabo has R70 and Ally has R35. What is the ratio of the amount of money Mabaso has, to the amount of money Thabo has and to the amount of money Ally has? Write the ratios in simplest form. The price of a steel table is R750. On Black Friday the table could be bought for R600. Calculate the percentage discount? Show ALL your calculations. Convert 125 g to kilograms. (1 kg = 1 000 grams) A green grocer packs 12 apples in a plastic bag. Calculate the number of bags he w need if he has 285 apples. The scale of a map is 1 500 000. Determine the actual distance in km if measurement on the map is 23,7 cm. Hint: 1 km = 100 000 cm
Answers
The actual distance represented by 23.7 cm on the map is 355.5 km.
To find the ratio of the amount of money Mabaso has to the amount of money Thabo has and the amount of money Ally has, we can divide each amount by the smallest amount (which is R35) to simplify the ratio.
Mabaso has R140, Thabo has R70, and Ally has R35.
The ratio of Mabaso's money to Thabo's money is:
R140 ÷ R35 = 4
The ratio of Mabaso's money to Ally's money is:
R140 ÷ R35 = 4
Therefore, the ratio of the amount of money Mabaso has to the amount of money Thabo has and to the amount of money Ally has is 4:1:1.
To calculate the percentage discount of a steel table, we need to find the difference between the original price and the discounted price, and then divide it by the original price. Finally, we multiply the result by 100 to get the percentage.
Original price: R750
Discounted price: R600
Discount: R750 - R600 = R150
Percentage discount: (R150 ÷ R750) × 100 = 20%
So, the table has a 20% discount on Black Friday.
To convert 125 grams to kilograms, we divide the amount in grams by 1,000 (since there are 1,000 grams in a kilogram).
125 g ÷ 1,000 = 0.125 kg
Therefore, 125 grams is equal to 0.125 kilograms.
If a green grocer packs 12 apples in a plastic bag and has 285 apples, we divide the total number of apples by the number of apples per bag to determine the number of bags needed.
Number of bags needed: 285 apples ÷ 12 apples/bag = 23.75 bags
Since we can't have a fraction of a bag, we round up to the nearest whole number. Therefore, the green grocer would need 24 bags.
If the scale of a map is 1,500,000 and the measurement on the map is 23.7 cm, we can use the scale to determine the actual distance.
1 cm on the map represents 1,500,000 cm in reality.
23.7 cm on the map represents x cm in reality.
x = 23.7 cm × 1,500,000 cm = 35,550,000 cm
To convert cm to km, we divide by 100,000 (since there are 100,000 cm in a kilometer).
35,550,000 cm ÷ 100,000 = 355.5 km
For more such questions on distance
https://brainly.com/question/30395212
#SPJ8
A random sample of 200 people was taken. 90 of the people in the sample favored Candidate A. We are interested in determining whether or not the proportion of the population in favor of Candidate A is significantly more than 40%. The test statistic is a.1.44. b.1.25. c..95. d..80.
Answers
Answer:
a. 1.44
Step-by-step explanation:
We are interested in determining whether or not the proportion of the population in favor of Candidate A is significantly more than 40%.
At the null hypothesis, it is tested if the proportion is of at most 40%, that is:
\(H_0: p \leq 0.4\)
At the alternative hypothesis, it is tested if the proportion is of more than 40%, that is:
\(H_1: p > 0.4\)
The test statistic is:
\(z = \frac{X - \mu}{\frac{\sigma}{\sqrt{n}}}\)
In which X is the sample mean, \(\mu\) is the value tested at the null hypothesis, \(\sigma\) is the standard deviation and n is the size of the sample.
0.4 is tested at the null hypothesis:
This means that \(p = 0.4, \sigma = \sqrt{0.4*0.6}\)
A random sample of 200 people was taken. 90 of the people in the sample favored Candidate A.
This means that:
\(n = 200, X = \frac{90}{200} = 0.45\)
Value of the test statistic:
\(z = \frac{X - \mu}{\frac{\sigma}{\sqrt{n}}}\)
\(z = \frac{0.45 - 0.4}{\frac{\sqrt{0.4*0.6}}{\sqrt{200}}}\)
\(z = 1.44\)
Thus the correct answer is given by option a.
the probability of an airline flight arriving on time at a certain airport is 84%, use a normal approximate to find the probability that more than 240 in a random sample of 400 commercial airline flights at the airport will arrive on time
Answers
The probability that more than 240 flights in a random sample of 400 commercial airline flights will arrive on time is approximately 1 or 100%.
To solve this problem using a normal approximation, we need to calculate the mean (μ) and standard deviation (σ) of the binomial distribution and then use the normal distribution to approximate the probability.
Given:
Probability of an airline flight arriving on time (success): p = 0.84
Number of trials (flights): n = 400
Number of flights arriving on time (successes): x > 240
First, we calculate the mean and standard deviation of the binomial distribution using the following formulas:
Mean (μ) = n * p
Standard Deviation (σ) = √(n * p * (1 - p))
μ = 400 * 0.84 = 336
σ = √(400 * 0.84 * 0.16) = √(53.76) ≈ 7.33
Now, we can use the normal distribution to find the probability that more than 240 flights will arrive on time. Since we're interested in the probability of x > 240, we will calculate the probability of x ≥ 241 and then subtract it from 1.
To use the normal distribution, we need to standardize the value of 240:
z = (x - μ) / σ
z = (240 - 336) / 7.33
z ≈ -13.13
Now, we can find the probability using the standard normal distribution table or a calculator. Since the value of z is extremely low, we can approximate it as:
P(x > 240) ≈ P(z > -13.13)
From the standard normal distribution table or calculator, we find that P(z > -13.13) is essentially 1 (close to 100%).
Therefore, the probability that more than 240 flights in a random sample of 400 commercial airline flights will arrive on time is approximately 1 or 100%.
For more such questions on probability , Visit:
https://brainly.com/question/24756209
#SPJ11
Differentiate y=x4 -x
Answers
Answer:
Step-by-step explanation:
To differentiate the function y = x^4 - x, we will use the power rule of differentiation. The power rule states that if f(x) = x^n, then the derivative of f(x) is f'(x) = nx^(n-1).
So, for y = x^4 - x, we can find the derivative as follows:
y' = 4x^3 - 1
So, the derivative of the function y = x^4 - x is y' = 4x^3 - 1.
Suppose you would like to deliver 20.6 terabytes data from Kansas City to Los Angeles. You have available a 1 Gbps dedicated link for data transfer. Would you prefer to transmit the data via this link or instead use USPS delivery knowing it will take them 2 days to complete the task? Explain.
Answers
Using proportions, it is found that the dedicated link would take 5.72 hours, which is significantly less time than the USPS delivery, hence the link should be used.
What is a proportion?A proportion is a fraction of a total amount, and the measures are related using a rule of three. Due to this, relations between variables, either direct(when both increase or both decrease) or inverse proportional(when one increases and the other decreases, or vice versa), can be built to find the desired measures in the problem, or equations to find these measures.
Each TB has 1000 GB, hence:
20.6 terabytes = 20,600 Gigabytes.
You have available a 1 Gbps dedicated link for data transfer, hence the time it would take for the transfer through the dedicated link is:
20,600/1 = 20,600 seconds.
Each hour has 3600 seconds, hence the time in hours is:
20600/3600 = 5.72 hours.
The dedicated link would take 5.72 hours, which is significantly less time than the USPS delivery, hence the link should be used.
More can be learned about proportions at https://brainly.com/question/24372153
#SPJ1
The cylinder shown below has a radius of 2 units and a height of 8 units.
8
-2
Which cylinder has the same volume as the cylinder above?
O A. cylinder with a radius of 8 units and a height of 2 units
O B. cylinder with a radius of 4 units and a height of 6 units
O C. cylinder with a radius of 4 units and a height of 4 units
O D. cylinder with a radius of 4 units and a height of 2 units
Answers
Match each function on the left to all points on the right that would be located on the graph of the function. Help!! thanks

Answers
Each function on the left should be matched to all points on the right that would be located on the graph of the function as follows;
f(x) = 2x + 2 ⇒ (0, 2).
f(x) = 2x² - 2 ⇒ (-1, 0).
\(f(x) = 2\sqrt{x+1}\) ⇒ (0, 2).
What is a function?In Mathematics and Geometry, a function is a mathematical equation which defines and represents the relationship that exists between two or more variables such as an ordered pair in tables or relations.
Next, we would determine the point or ordered pair that represent a solution on the graph of each of the function as follows;
For the ordered pair (0, 2), we have:
f(x) = 2x + 2
2 = 2(0) + 2
2 = 2 (True).
For the ordered pair (-1, 0), we have:
f(x) = 2x² - 2
0 = 2(-1)² - 2
0 = 2 - 2
0 = 0 (True).
For the ordered pair (0, 2), we have:
\(f(x) = 2\sqrt{x+1}\\\\2= 2\sqrt{0+1}\\\\2 = 2\sqrt{1}\)
2 = 2 (True).
Read more on function here: https://brainly.com/question/10687170
#SPJ1
The lines represented by the equations y = -X – 3 and
5y + 5x = -15 are
neither parallel nor perpendicular
Submit Answer
the same line
parallel
perpendicular
What is the answer?
Answers
Answer:
The lines represented by the equations y = -X – 3 and
5y + 5x = -15
Step-by-step explanation:
neither are parallel nor perpendicular
Submit Answer
the same line
parallel
perpendicular
What is the answer?
NO LINKS!! URGENT HELP PLEASE!!!
Please help me with Growth rate and Initial Value only

Answers
Answer:
growth rate: 4
y-value: 19
equation: y=4x+19
Step-by-step explanation:
Growth Rate:
The growth rate of a linear function is constant. This means that the function will increase or decrease by the same amount for every unit increase in x.
This can be found by dividing the change in y-values by the change in x-values.
For the question:
The change in y-values is 11-7=4,
and the change in x-values is +1.
Therefore, the growth rate is 4.
\(\hrulefill\)
Initial Value: The initial value of a linear function is the value of the function when x is 0.
In this case, the initial value is 19.
This can be found by looking at the y-value of the point where x is 0.
In this case, the y-value is 19.
\(\hrulefill\)Equation: The equation of a linear function is y = mx + b, where m is the slope and b is the y-intercept.
Using the table you provided, we can find the slope by using two points on the line.
Let’s use (-3, 7) and (1, 23).
The slope is (y2-y1)/(x2-x1)=(23-7)(1-(-3)=16/4=4
Now,
Taking 1 point (-3,7) and slope 4.
we can find the equation by using formula:
y-y1=m(x-x1)
y-7=4(x+3)
y=4x+12+7
y=4x+19
Therefore, the equation of the given table is y=4x+19\(\hrulefill\)
Answer:
Growth rate: 4
Initial value: 19
Equation: y = 4x + 19
Step-by-step explanation:
The slope of a linear function represents its growth rate.
Therefore, the growth rate of a linear function can be found using the slope formula.
Substitute two (x, y) points from the table into the slope formula, and solve for m. Substituting points (0, 19) and (1, 23):
\(\textsf{slope}\:(m)=\dfrac{y_2-y_1}{x_2-x_1}=\dfrac{23-19}{1-0}=\dfrac{4}{1}=4\)
Therefore, the growth rate of the linear function is 4.
The initial value of a linear function refers to the y-intercept, which is the value of the y when x = 0.
From inspection of the given table, y = 19 when x = 0.
Therefore, the initial value of the linear function is 19.
To write a linear equation given the growth rate (slope) and initial value (y-intercept), we can use the slope-intercept formula, which is y = mx + b. The slope is represented by the variable m, and the y-intercept is represented by the variable b.
As the growth rate of the given linear function is 4, and the initial value is 19, substitute m = 4 and b = 19 into the slope-intercept formula to create the equation of the linear function represented by the given table:
\(\boxed{y=4x+19}\)
A shopkeeper has 2425 boxes of 24 pencils each. How many pencils do all the boxes have in all?
Answers
Answer:A shopkeeper has 2425 boxes of 24 pencils each. How many pencils do all the boxes have in all?
Step-by-step explanation:
Crystal has 25 lollipops. Angie has 12 more lollipops than Crystal.
How many lollipops do the girls have all together?
Answers
Answer:
Both the girls have 62 lollipops
Step-by-step explanation:
25+25=50
50+12=62
Answer:
62 lollipops
Step-by-step explanation:
If Angie has 12 more lollipops than Crystal...
25 + 12 = 37 lollipops
Angie has 37 lollipops and Crystal has 25 lollipops. In total, that is...
37 + 25 = 62 lollipops
A student's course grade is based on one midterm that counts as 10% of his final grade, one class project that counts as 5% of his final grade, a set of homework assignments that counts as 45% of his final grade, and a final exam that counts as 40% of his final grade. His midterm score is 60, his project score is 80, his homework score is 75, and his final exam score is 78. What is his overall final score? What letter grade did he earn (A, B, C, D, or F)? Assume that a mean of 90 or above is an A, a mean of at least 80 but less than 90 is a B, and so on.
Answers
Answer:
His overall final score is a 73, which means that that student recieved a letter grade of a C.
Step-by-step explanation:
First, we are finding the mean of the scores to average everything out.
So, start by adding up all the scores given: 60+80+75+78=293.
Then, divide that sum by the number of scores given: 293/5=73.25, or rounded to a whole number is a 73.
In most schools, a 73 is a C, so this students letter grade for this course is a C.
Supervisor: "I see that 1000 calls were sent to your extension this month. 15% of those calls were not answered, which means that you did not answer __________ calls this month."
Answers
Step-by-step explanation:
850 calls
1000:100=10
1%=10
10×85=850
Discount is the reduction in value. The total number of calls not answered this is 150 calls
Discount and percentagesGiven the following
Total number of calls = 1000 calls
If 15% of those calls were not answered, the total calls that were not answered is given as:
Total call not answered . = 0.15 * 1000
Total call not answered = 150 calls
Hence the total number of calls not answered this is 150 calls
Learn more on percentages here: https://brainly.com/question/24304697
#SPJ2
if it costs £12 for 4 cakes, what is the cost of 6 cakes?
Answers
The mean cost of a five pound bag of shrimp is 40 dollars with a standard deviation of 8 dollars.
If a sample of 49 bags of shrimp is randomly selected, what is the probability that the sample mean would be less than 37.4 dollars? Round your answer to four decimal places.
Answers
Answer:
The mean of the sample distribution of the sample mean is the same as the population mean, which is 40 dollars. The standard deviation of the sample distribution of the sample mean (also called the standard error) is given by:
standard error = standard deviation / sqrt(sample size) = 8 / sqrt(49) = 8 / 7
To find the probability that the sample mean would be less than 37.4 dollars, we need to standardize the sample mean using the standard error and then look up the probability from a standard normal distribution table. The z-score for a sample mean of 37.4 dollars is:
z = (37.4 - 40) / (8 / 7) = -1.225
Looking up this z-score in a standard normal distribution table, we find that the probability of getting a sample mean less than 37.4 dollars is 0.1103 (rounded to four decimal places). Therefore, the probability that the sample mean would be less than 37.4 dollars is 0.1103.
give thanks, your welcome <3
Step-by-step explanation:
Solve: 3(2d - 1) – 2d = 4(d– 2) + 5

Answers
The right answer is No solution.
Look at the attached picture
Hope it will help you

Tell whether each equation is True, False, or Open. Explain. "must explain for credit"
1. 6-t=12
2. 7+(-5)=12
3. 31 - 15 = 22 + (-3)2
