Answers
Viktor is in the 60th percentile, which is 85, while the percentile for 71 is 26.666.
What is percentile?Percentile is defined as the value below which a given percentage falls under. Ben, for instance, is the fourth tallest child in a group of 20, and eighty percent of the kids are shorter than you. As a result, Ben is in the 80th percentile.
We have the data
Sort the data as follows: 58, 64, 66, 70, 71, 75, 77, 80, 84, 85, 87, 90, 93, 95, 96
employing the percentile formula,
Percentile is calculated as follows: 71 Percentile
(4 / 15)*100 Percentile
26.666 Percentile = (Number of Values Below "x" / Total Number of Values) 100
Consequently, 71's percentile is equal to 26.666.
Identifying the rank
Thus, the ranking is 0.6.
To find the rank for viktor
Find the percentile using the formula,
Percentile = Rank × Total number of the data set
Percentile = 0.6 × 15
Percentile = 9
Now, counting 9 values from left to right we reach 85, and we can say that all the values below 85 will come under the 60th percentile. In other words, 60% of the values are below 85.
The 60th percentile is 85
Thus viktor is in 60th percentile is 85
To know more about Percentile click the link:
brainly.com/question/1561673
#SPJ1
Related Questions
Determine the number that will complete the square to solve each equation after the constant term has been written on the right side. Do not actually solve. 3 w^{2}-w-24=03w 2 −w−24=0
Answers
The number that will complete the square to solve equation is 1/36.
What is completing the square?
For some values of h and k, completing the square is an elementary algebraic method for changing a quadratic polynomial of the form
ax^2 + bx + c to the form a^2 + k. In other words, the quadratic expression is completed by inserting a perfect square trinomial.
Consider, the given polynomial
3w^2 - w - 24 = 0
Rewrite the polynomial in the form ax^2 + bx = c
Add 24 on both sides,
3w^2 - w - 24 + 24 = 24
⇒ 3w^2 - w = 24
Divide both sides by 3,
\(w^2-\frac{1}{3}w = 8\)
To complete the square x^2 + bx, we add \((\frac{b}{2} )^2\)
Here, b = -1/3
So, \((\frac{b}{2})^2 = (\frac{-1/3}{2})^2 = (-\frac{1}{6})^2 = \frac{1}{36}\)
Adding to both sides of the equation, we have
\(w^2-\frac{1}{3}w+\frac{1}{36} = 8+\frac{1}{36}\)
Hence, the number that will complete the square to solve an equation is 1/36.
To know more about completing the square, click on the link
https://brainly.com/question/13981588
#SPJ4
Place the daily temperatures of the following States from top to bottom coldest to warmest.
Alaska -35
=
Hawali 52
Colorado -3
Oregon-12
Florida 49
Arizona 36
Main -22
California 58
Answers
Main
Oregon
Colorado
Arizona
Florida
Hawaii
Cali
Solve and simplify: -9/10 ÷ (-3/10) = *
Answers
Answer: 3
Step-by-step explanation:
Answer: 3
Step-by-step explanation: the equation is the question. XD
James have 18 litres of water. He poured unequally into 3 tank
I. Poured three quarter of water from tank one into tank 2
II. Poured half of the water that is now in tank 2 into tank 3
III. Poured one third of water that is now in tank 3 into tank 1
Find how much water is in each tanks
Answers
Answer:
ames have 18 litres of water. He poured unequally into 3 tank
I. Poured three quarter of water from tank one into tank 2
II. Poured half of the water that is now in tank 2 into tank 3
III. Poured one third of water that is now in tank 3 into tank 1
Find how much water is in each tanks
Step-by-step explanation:
Let's start with the amount of water in tank 1 as x liters.
I. Poured three quarter of water from tank one into tank 2, so tank 1 now has 1/4 of x liters and tank 2 has 3/4 of x liters.
II. Poured half of the water that is now in tank 2 into tank 3, so tank 2 now has 3/8 of x liters and tank 3 has 3/8 of x liters.
III. Poured one third of water that is now in tank 3 into tank 1, so tank 3 now has 1/3 * 3/8 * x = 1/8 * x liters and tank 1 has 1/4 * x + 1/8 * x = 3/8 * x liters.
We know that James poured 18 liters of water into the three tanks, so the sum of the water in the three tanks must be 18 liters.
3/8 * x + 3/8 * x + 1/8 * x = 18
Simplifying the equation, we get:
7/8 * x = 18
x = 18 * 8 / 7 = 20.57 (rounded to two decimal places)
Therefore, the amount of water in each tank is:
Tank 1: 3/8 * x = 7.71 liters
Tank 2: 3/8 * x = 7.71 liters
Tank 3: 1/8 * x = 2.57 liters
I need to determine which system of equations it is a solution too if any

Answers
To solve this exercise you have to solve each system of equations.
a)
\(\begin{cases}y=4x-5 \\ y=-6x+25\end{cases}\)To solve this equation system you have to equal both equations and solve for x:
\(4x-5=-6x+25\)- Pass -6x to the left side of the equation by applying the opposite operation to both sides of it
\(\begin{gathered} 4x+6x-5=-6x-6x+25 \\ 10x-5=25 \end{gathered}\)- Add 5 to both sides of the equal sign:
\(\begin{gathered} 10x-5+5=25+5 \\ 10x=30 \end{gathered}\)- Divide both sides by 10
\(\begin{gathered} \frac{10x}{10}=\frac{30}{10} \\ x=3 \end{gathered}\)- Replace the value of x in one of the equations and solve for y:
\(\begin{gathered} y=4x-5 \\ y=4\cdot3-5 \\ y=12-5 \\ y=7 \end{gathered}\)The solution for this equation system is (3,7)
b)
\(\begin{cases}2y=10x-12 \\ y=-7x+42\end{cases}\)Replace the second equation into the first one:
\(\begin{gathered} 2y=10x-12 \\ 2(-7x+42)=10x-12 \end{gathered}\)- Distribute the multiplication on the parentheses term:
\(\begin{gathered} 2\cdot(-7x)+2\cdot42=10x-12 \\ -14x+84=10x-12 \end{gathered}\)-Subtract 10x to both sides of the expression:
\(\begin{gathered} -14x-10x+84=10x-10x-12 \\ -24x+84=-12 \end{gathered}\)-Subtract 84 to both sides of the equal sign:
\(\begin{gathered} -24x+84-84=-12-84 \\ -24x=-96 \end{gathered}\)-Divide both sides by -24
\(\begin{gathered} \frac{-24x}{-24}=\frac{-96}{-24} \\ x=4 \end{gathered}\)- Replace the value of x in the second equation and solve for y:
\(\begin{gathered} y=-7x+42 \\ y=-7\cdot4+42 \\ y=-28+42 \\ y=14 \end{gathered}\)The solution for this equation system is (4,14)
c)
\(\begin{cases}3y-9x=-21 \\ y+12x=23\end{cases}\)- Write the second equation for y:
\(\begin{gathered} y+12x=23 \\ y+12x-12x=23-12x \\ y=-12x+23 \end{gathered}\)- Replace the expression in the first equation
\(\begin{gathered} 3y+9x=-21 \\ 3(-12x+23)+9x=-21 \end{gathered}\)-Distribute the multiplication on the parentheses term
\(\begin{gathered} 3\cdot(-12x)+3\cdot23-9x=-21 \\ -36x+96-9x=-21 \\ -36x-9x+69=-21 \\ -45x+69=-21 \end{gathered}\)- Subtract 69 to both sides of the equal sign
\(\begin{gathered} -45x+69-69=-21-69 \\ -45x=-90 \end{gathered}\)-Divide both sides by -45
\(\begin{gathered} \frac{-45x}{-45}=\frac{-90}{-45} \\ x=2 \end{gathered}\)-Replace the value of x in the expression obtained for y and solve:
\(\begin{gathered} y=-12x+23 \\ y=-12\cdot2+23 \\ y=-24+23 \\ y=-1 \end{gathered}\)The solution of this equation system is (2,-1)
d)
\(\begin{cases}2y-21x=-24 \\ 2y+8x=52\end{cases}\)- Write the second equation for y:
\(\begin{gathered} 2y+8x=52 \\ 2y+8x-8x=52-8x \\ 2y=52-8x \\ \frac{2y}{2}=\frac{52}{2}-\frac{8x}{2} \\ y=-4x+26 \end{gathered}\)-Replace the expression in the first equation:
\(\begin{gathered} 2y-21x=-24 \\ 2(-4x+26)-21x=-24 \end{gathered}\)-Distribute the multiplication on the parentheses term:
\(\begin{gathered} 2*\mleft(-4x\mright)+2*26-21x=-24 \\ -8x+52-21x=-24 \\ -8x-21x+52=-24 \\ -29x+52=-24 \end{gathered}\)-Subtract 52 to both sides of the equation:
\(\begin{gathered} -29x+52-52=-24-52 \\ -29x=-76 \end{gathered}\)-Divide both sides by -29
\(\begin{gathered} \frac{-29x}{-29}=\frac{-76}{-29} \\ x=\frac{76}{29} \end{gathered}\)-Replace this value in the expression obtained for y:
\(\begin{gathered} y=-4x+26 \\ y=-4\cdot\frac{76}{29}+26 \\ y=-\frac{304}{29}+26 \\ y=\frac{450}{29} \end{gathered}\)The solution to this equation system is (76/29,450/29)
The answer for this exercise is:
a → (3,7)
c → (2,-1)
b → (4,14)
e → (4,20)
student x pushes a 10-n box with a force of 2 n. at the same time, student y pushes the same box with a force of 6 n, but in the opposite direction. which would most likely occur? (ignore friction.)
Answers
Solve for x on the diagram below

Answers
The value of x in the diagram is 100 degrees
How to determine the value of xFrom the question, we have the following parameters that can be used in our computation:
The figure
On the figure, we can see that:
The angle x and 100 degrees are alternate angles
Alternate angles have equal values
So, we have
x = 100
Hence, the value is 100 degree
Read more about angle at
https://brainly.com/question/25716982
#SPJ1
4. Sketch two vectors a
=⟨3,1⟩ and b
=⟨1,2⟩ Now use two ways to geometrically find their sum, s
and represent s
in component form. Sketch vector of their difference d
= a
− b
then vector i
and −2 b
. Find ∣ j
− b
∣ and the unit vector in direction of b
.
Answers
the sum s = ⟨4,3⟩
d = ⟨3-1, 1-2⟩ = ⟨2,-1⟩
∣ j - b ∣ = √2
the unit vector in the direction of b is given by b/∣ b ∣ = ⟨1/√5, 2/√5⟩.
Geometrically, we can find the sum s = a + b in two ways:
1. Triangle Method: To find the sum s, we can place the initial point of vector b at the terminal point of vector a. The sum s is then the vector that starts from the initial point of vector a and ends at the terminal point of vector b. By connecting these points, we obtain the sum s = ⟨4,3⟩.
2. Parallelogram Method: To find the sum s, we can construct a parallelogram with vector a and vector b as adjacent sides. The sum s is then the diagonal of the parallelogram starting from the common initial point of a and b. By connecting these points, we obtain the sum s = ⟨4,3⟩.
Next, we can find the difference d = a - b by subtracting the components of vector b from vector a. Therefore, d = ⟨3-1, 1-2⟩ = ⟨2,-1⟩.
To find the vector i and -2b, we can multiply the vector b by -2, which gives us -2b = -2⟨1,2⟩ = ⟨-2,-4⟩. The vector i can be represented as a unit vector in the x-direction, so i = ⟨1,0⟩.
To find the magnitude of j - b, we subtract the components of vector b from vector j: j - b = ⟨0,1⟩ - ⟨1,2⟩ = ⟨-1,-1⟩. The magnitude of j - b, denoted as ∣ j - b ∣, can be calculated as the length of the vector √((-1)² + (-1)²) = √2.
Lastly, to find the unit vector in the direction of vector b, we divide vector b by its magnitude. The magnitude of b, denoted as ∣ b ∣, can be calculated as the length of the vector √(1² + 2²) = √5. Therefore, the unit vector in the direction of b is given by b/∣ b ∣ = ⟨1/√5, 2/√5⟩.
Learn more about vector here
https://brainly.com/question/24256726
#SPJ4

The radius of a circle is 4 yards. What is the circle's circumference?
r=4 yd
Use 3.14 for .
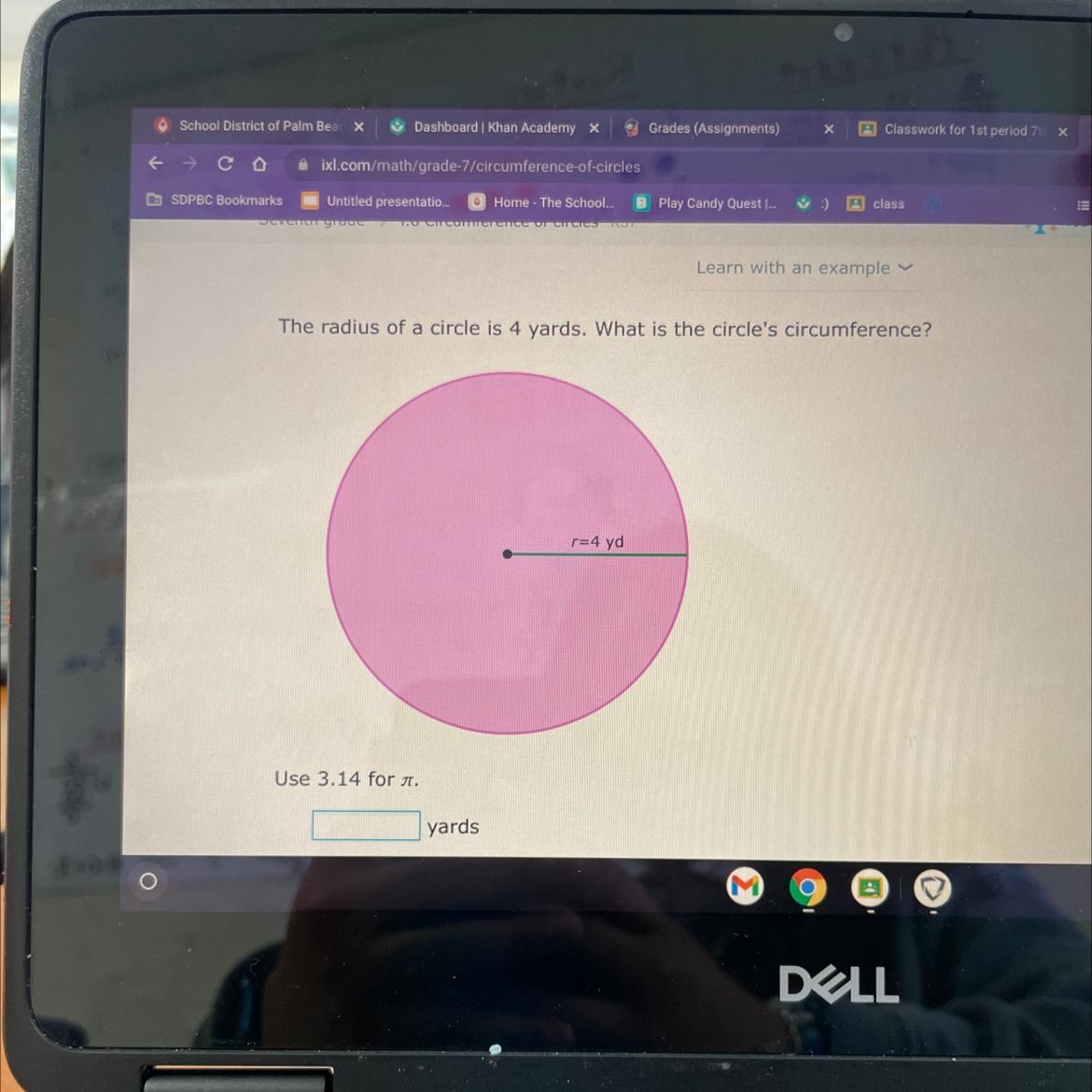
Answers
Answer:
25.12 yd
Step-by-step explanation:
Radius (r) = 4 yd
π = 3.14
Circumference of the circle
= 2πr
= 2 × (3.14) × (4)
= 25.12 yd
_________
Hope it helps ⚜
Answer:
25.12 yards
Step-by-step explanation:
Circumference formula : 2πr
r = radiusSolving
C = 2πrC = 2 x 3.14 x 4 [given π = 3.14 and r = 4]C = 3.14 x 8C = 25.12 yardsData set 2 is symmetric The prices for six books are given below. If all the prices are reduced by 50%, what is the new median price? $12.75, $14.80, $19.99 $9.95 $16.00, $17.95 (A) $7.40 (B) $7.70 (C) $15.24 (D) $15.40
Answers
After reducing all the book prices by 50%, the new median price is determined to be $7.70 (B)
To find the new median price after reducing all the book prices by 50%, we first need to calculate the reduced prices. By reducing each given price by 50%, we get $6.375, $7.40, $9.995, $4.975, $8.00, and $8.975 respectively.
Next, we arrange these reduced prices in ascending order: $4.975, $6.375, $7.40, $8.00, $8.975, and $9.995. The median is the middle value in this ordered list. Since there are six prices, the middle two values are $7.40 and $8.00.
To find the median, we take the average of these two values, which gives us ($7.40 + $8.00) / 2 = $7.70.
Therefore, the new median price, after reducing all the book prices by 50%, is $7.70 (B). This means that the median price of the books, after the reduction, is $7.70.
Learn more about Median
brainly.com/question/11237736
#SPJ11
choose the definition for the function y={x+1 x≤2 x+2 x>2 y={x+1 x>2 x+2 x≤2 y={x+1 x

Answers
Answer:
D
Step-by-step explanation:
Suppose iq scores were obtained for randomly selected sets of. The pairs of measurements yield , , r, p-value0. 000, and , where x represents the iq score of the. Find the best predicted value of given that the has an iq of ? use a significance level of 0. 5.
Answers
Without the values of x and r, we cannot determine the best predicted value.
To find the best predicted value of y given that the person has an IQ of x, we can use the regression equation y = a + bx, where a is the y-intercept and b is the slope of the regression line. From the given information, we have the following values:
x = ?, r = ?, p-value = 0.000. To calculate the best predicted value, we need the values of a and b. The p-value being less than the significance level of 0.5 indicates that the correlation between x and y is statistically significant.
However, without the values of x and r, we cannot determine the best predicted value.
To more about correlation visit:
https://brainly.com/question/30116167
#SPJ11
A phone company offers two monthly plans. Plan A costs $27 plus an additional $0.15 for each minute of calls. Plan B has no initial fee but costs $0.19 for each minute of calls.
For what amount of calling do the two plans cost the same?
What is the cost when the two plans cost the same?
Answers
Answer:
To find the amount of calling that makes the two plans cost the same, we have to set the cost of Plan A equal to the cost of Plan B and solve for the number of minutes.
Let x be the number of minutes of calls.
For Plan A, the cost is given by:
CostA = 27 + 0.15x
For Plan B, the cost is given by:
CostB = 0.19x
Setting the two costs equal, we get:
27 + 0.15x = 0.19x
Simplifying the equation, we get:
0.04x = 27
Solving for x, we get:
x = 675
Therefore, when the number of minutes of calls is 675, the two plans cost the same.
To find the cost when the two plans cost the same, we can substitute x = 675 into either CostA or CostB. For example, using CostA, we get:
CostA = 27 + 0.15(675) = 27 + 101.25 = $128.25
Therefore, when the number of minutes of calls is 675, the cost of both plans is $128.25.
who doesnt just use this for the awnsers
Answers
There are 30 names in a hat. If two names are picked without replacement, which expression shows the probability that Jack and Jill will be picked?

Answers
Answer: Choice C)
(1/30)*(1/29)
Explanation:
Jack has a 1/30 chance of being picked since he is 1 person out of 30 total. After his name is picked, and not put back, there are 30-1 = 29 names left. The chances Jill is picked is 1/29. The two fractions are multiplied to get the overall probability both are picked.
the solution of the following equation as 0.15 ( 10t - 9= 0.75 (4t - 3)
Answers
Answer:
\(\huge\boxed{\sf t = 0.6}\)
Step-by-step explanation:
\(\sf 0.15(10t-9) = 0.75(4t-3)\\\\Resolving \ Parenthesis\\\\1.5t-1.35 = 3t - 2.25\\\\Combining \ like \ terms\\\\-1.35 + 2.25 = 3t-1.5t\\\\0.9 = 1.5t\\\\Dividing \ both \ sides \ by \ 1.5\\\\0.9/1.5 = t\\\\0.6 = t\\\\OR\\\\\bold{t = 0.6}\)
Hope this helped!
~AnonymousHelper1807Factor the polynomial.
5x4 + 10x3 + 15x2
Answers
Answer:
5x^2(x^2 + 2x + 3)
Step-by-step explanation:
All the terms can be factored by 5 and x^2, so we get:
5x^2(x^2 + 2x + 3)
there are no more common terms so this is the answer
the edge of a cube has a length of inches with a possible error of % the possible error in cubic inches in the volume of the cube is
Answers
The possible error in the volume of the cube is cubic inches.
The edge of a cube with a length of inches and a possible error of % means that the actual length could be within % of the given length. Therefore, the minimum possible length of the edge is inches, and the maximum possible length is inches.
To calculate the possible error in cubic inches in the volume of the cube, we need to use the formula V = e^3, where V is the volume and e is the length of the edge.
Substituting the minimum and maximum values of the edge length, we get the minimum and maximum possible volumes of the cube:
V_min = ( inches)^3 = cubic inches
V_max = ( inches)^3 = cubic inches
The difference between the maximum and minimum volumes is the possible error in cubic inches:
V_error = V_max - V_min = ( inches)^3 - ( inches)^3 = cubic inches
Therefore, the possible error in the volume of the cube is cubic inches. This means that the actual volume of the cube could be within cubic inches of the given volume.
Learn more about volume brainly.com/question/1578538
#SPJ11
When constructing a confidence interval for a difference between two population proportions, why is it important to check that the number of successes and the number of failures in each sample is at least 10? Select the correct answer
A. So we can assume that the two samples are independent.
B. So we can assume the sampling distribution of Di-D is approximately Normal,
C. So we can assume that the observations within each sample are independent
D. So we can assume that population 1 and population 2 are approximately Normal.
E. So we can generalize the results to the populations from which the samples were selected.
Answers
The correct option is B. When constructing a confidence interval for a difference between two population proportions, it is important to check that the number of successes and the number of failures in each sample is at least 10 because it allows us to assume that the sampling distribution of Di-D is approximately normal.
So we can assume the sampling distribution of Di-D is approximately Normal.
In statistics, the confidence interval is a statistical measure used to calculate the degree of certainty in a statistical inference. It is a range of values around a point estimate of a population parameter within which the true population parameter is expected to fall with a given level of probability.
The confidence interval for a difference between two population proportions is calculated using the standard error of the difference between the sample proportions (SE p1 - p2).
The sampling distribution of the difference between the two sample proportions is approximately normal when the number of successes and failures in each sample is at least 10.
If the number of successes and failures is less than 10, the sampling distribution of Di-D may not be normal, and using a normal distribution to construct a confidence interval would not be appropriate.
Hence, it is important to check that the number of successes and the number of failures in each sample is at least 10 to assume the sampling distribution of Di-D is approximately normal.
To know more about sampling visit:
https://brainly.com/question/31890671
#SPJ11
find the volume of the solid enclosed by the paraboloids z = 4 \left( x^{2} y^{2} \right) and z = 8 - 4 \left( x^{2} y^{2} \right).
Answers
We are given that two paraboloids are given by the following equations:z = 4(x^2y^2)z = 8 - 4(x^2y^2)We need to find the volume of the solid enclosed by these two paraboloids.
Let's first graph the paraboloids to see how they look. The graph is shown below:Volume enclosed by the two paraboloidsThe solid that we need to find the volume of is the solid enclosed by the two paraboloids. To find the volume, we need to find the limits of integration. Let's integrate with respect to x first. The limits of x are from -1 to 1. To find the limits of y, we need to solve the two equations for y. For the equation z = 4(x^2y^2), we get y = sqrt(z/(4x^2)). For the equation z = 8 - 4(x^2y^2), we get y = sqrt((8-z)/(4x^2)). Thus the limits of y are from 0 to the minimum of these two equations, which is given by y = min(sqrt(z/(4x^2)), sqrt((8-z)/(4x^2))).We are now ready to find the volume. The integral that we need to evaluate is given by:∫(∫(4(x^2y^2) - (8 - 4(x^2y^2)))dy)dx∫(∫(4x^2y^2 + 4(x^2y^2) - 8)dy)dx∫(∫(8x^2y^2 - 8)dy)dxThe limits of y are from 0 to min(sqrt(z/(4x^2)), sqrt((8-z)/(4x^2))). The limits of x are from -1 to 1. Thus we get:∫(-1)1∫0min(sqrt(z/(4x^2)), sqrt((8-z)/(4x^2)))(8x^2y^2 - 8)dydxAnswer more than 100 words:Using the above equation, we can evaluate the integral by making a substitution y = sqrt(z/(4x^2)). Thus, we get dy = sqrt(1/(4x^2)) dz. We can then replace y and dy in the integral to get:∫(-1)1∫04(x^2)(z/(4x^2))(8x^2z/(4x^2) - 8)sqrt(1/(4x^2))dzdx∫(-1)1∫04z(2z - 2)sqrt(1/(4x^2))dzdx∫(-1)1∫04z^2 - zsqr(1/(x^2))dzdx∫(-1)1∫04z^2 zsqr(1/(x^2))dzdx∫(-1)1(16/3)x^2dx∫(-1)11(16/3)dx(16/3)∫(-1)1x^2dxThe last integral can be easily evaluated to give:∫(-1)1x^2dx = (1/3)(1^3 - (-1)^3) = (2/3)Thus, we get the volume of the solid enclosed by the two paraboloids as follows:Volume = (16/3) x (2/3) = 32/9Thus, the volume of the solid enclosed by the two paraboloids is 32/9. Therefore, the main answer is 32/9.
The volume of the solid enclosed by the two paraboloids z = 4(x²y²) and z = 8 - 4(x²y²) is 32/9 cubic units. We used the limits of integration and integrated with respect to x and y.
To learn more about Integration click:
brainly.com/question/31744185
#SPJ11
The volume of the solid enclosed by the paraboloids \(z = 4 (x^2y^2)\) and \(z = 8 - 4 (x^2y^2)\) can be found using the triple integral. The triple integral is given as: \(\int\int\int\) dV where the limits of the integrals depend on the bounds of the solid. The bounds can be found by equating the two paraboloids and solving for the values of x, y and z.
The two paraboloids intersect at \(z = 4 (x^2y^2) = 8 - 4 (x^2y^2)\) which simplifies to \((x^2y^2) = 1/2\). Thus, the bounds of the solid are:\(0 \leq z \leq 4 (x^2y^2)0 \leq z \leq 8 - 4 (x^2y^2)0 \leq x^2y^2 \leq 1/2\) the bounds for x and y are symmetric and we can integrate the solid using cylindrical coordinates.
Thus, the integral becomes:\(\int\int\int\) r dz r dr dθwhere r is the distance from the origin and θ is the angle from the positive x-axis. Substituting the bounds, we get:\(\int0^2\ \pi \int0\sqrt(1/2) \int4 (r^2\cos^2\ \theta\sin^2\theta) r\ dz\ dr\ d\ \theta + \int0^2\ \pi \int \sprt(1/2)^1 \int8 - 4 (r^2cos^2\thetasin^2\theta)\)solving this integral, we get the volume of the solid.
he volume of the solid enclosed by the paraboloids \(z = 4 (x^2y^2)\) and \(z = 8 - 4 (x^2y^2)\) is given as: \(8\pi /3\)
To know more about volume visit -
brainly.com/question/30681924
#SPJ11
Drag each system of equations to the correct location on the table. Classify each system of equations as having a single solution, no solution, or infinite solutions. Y = 5 − 2x 4x 2y = 10 x = 26 − 3y 2x 6y = 22 5x 4y = 6 10x − 2y = 7 x 2y = 3 4x 8y = 15 3x 4y = 17 -6x = 10y − 39 x 5y = 24 5x = 12 − y.
Answers
The given system of equations has one solution, no solution, or infinitely many solutions as shown above.
Given system of equations: Y
= 5 − 2x 4x 2y
= 10 x
= 26 − 3y 2x 6y
= 22 5x 4y
= 6 10x − 2y
= 7 x 2y
= 3 4x 8y
= 15 3x 4y
= 17 -6x
= 10y − 39 x 5y
= 24 5x
= 12 − y
To classify the given system of equations, we need to put the equations in a table and then we will find out the value of x and y. If there is a unique solution for x and y, then the given system of equations will have a single solution. If the given system of equations is inconsistent, then it will have no solution and if it is consistent then it will have infinitely many solutions.Now we will classify the given system of equations as having a single solution, no solution, or infinite solutions.Single solution No solution Infinite solutions
Y
= 5 − 2x 4x2y
= 10x
= 26 − 3y 2x6y
= 225x4y
= 610x − 2y
= 7x2y
= 34x8y
= 153x4y
= 17-6x
= 10y − 39x5y
= 245x
= 12 − y.
The given system of equations has one solution, no solution, or infinitely many solutions as shown above.
To know more about infinitely visit:
https://brainly.com/question/32237150
#SPJ11
Currently I have separators on my molars so I can have enough space for an expander. But I noticed that one of my molars has shifted a lot to the side where it’s uncomfortable to eat or bite down. And I’m not sure if it’s suppose to shift to the side or not
Is that normal?-
Answers
Answer:
Yes I think
Step-by-step explanation:
I went through the braces process a few years ago and I got an expander. Your separator is probably making room for something meaning your teeth will probably move. Im no professional so Id say call into the office tomorrow or asap. And for the pain use whatever pain meds they allow (normally ibprophen ot tylenol) (sorry for spelling)
Divide the following expression using long division to find the quotient. a. (8x³-22x²-16x+21)÷(-4x+3) b. (9x³-6x²-8x-66)÷(3x-7)
Answers
a. the quotient is 8x² - 16 + 4x - 4 with a remainder of 18. b. the quotient is 3x² + 5 - 3/(3x - 7).
a. To divide the expression (8x³-22x²-16x+21) by (-4x+3) using long division, we follow these steps:
markdown
Copy code
________________________
(-4x+3) | 8x³ - 22x² - 16x + 21
- (8x³ - 6x²)
________________________
-16x² - 16x
+ (16x² - 12x)
________________________
-4x + 21
+ (4x - 3)
________________________
18
Therefore, the quotient is 8x² - 16 + 4x - 4 with a remainder of 18.
b. To divide the expression (9x³ - 6x² - 8x - 66) by (3x - 7) using long division, we follow these steps:
markdown
Copy code
________________________
(3x - 7) | 9x³ - 6x² - 8x - 66
- (9x³ - 21x²)
________________________
15x² - 8x - 66
+ (15x² - 35x)
________________________
27x - 66
- (27x - 63)
________________________
-3
Therefore, the quotient is 3x² + 5 - 3/(3x - 7).
Learn more about quotient here
https://brainly.com/question/11418015
#SPJ11
f(x,y)=x 2−y 2,x 2+y 2 =81 maximum value minimum value
Answers
The maximum value of the function `f(x,y) = x^2−y^2` subject to the constraint `x^2 + y^2 = 81` is `243` and the minimum value is `-81`.
Given, `f(x,y)=x^2−y^2, x^2+y^2 =81`To find the maximum and minimum value of the given function, we can use Lagrange multiplier.
Let `g(x,y) = x^2 + y^2 = 81`
Using Lagrange multiplier, we can form a new function
`F(x,y) = f(x,y) + λg(x,y)
`Where `λ` is the Lagrange multiplier.
Now, `F(x,y) = x^2−y^2 + λ(x^2 + y^2 − 81)`
Differentiating `F(x,y)` w.r.t `x`, we get:`
∂F/∂x = 2x + 2λx`
Differentiating `F(x,y)` w.r.t `y`, we get:
`∂F/∂y = −2y + 2λy`
Differentiating `F(x,y)` w.r.t `λ`, we get:`
∂F/∂λ = x^2 + y^2 − 81`
Equating these to zero, we get:`
2x + 2λx = 0`and,`−2y + 2λy = 0`and,
`x^2 + y^2 − 81 = 0`
Simplifying, we get:`
x(1 + λ) = 0`and,`y(λ − 1) = 0`and,`x^2 + y^2 = 81`
Now, there are three possibilities:
`Case 1:
λ = -1`
From the above two equations, we get that either `x = 0` or `y = 0`.
If `x = 0`, then `y = ±9`.If `y = 0`, then `x = ±9`.
So, we have four critical points:`
(0,9), (0,-9), (9,0), (-9,0)
`Let's evaluate the function at these points:
`f(0,9) = -81``f(0,-9) = -81``f(9,0) = 81``f(-9,0) = 81`
So, the maximum value of `f(x,y)` is `81` and the minimum value is `-81`.
`Case 2:
λ = 1`
From the above two equations, we get that either `x = 0` or `y = 0`.If `x = 0`, then `y = ±9`.
If `y = 0`, then `x = ±9`.
So, we have four critical points:`
(0,9), (0,-9), (9,0), (-9,0)`
Let's evaluate the function at these points:`
f(0,9) = -81
``f(0,-9) = -81``
f(9,0) = 81``
f(-9,0) = 81
`So, the maximum value of `f(x,y)` is `81` and the minimum value is `-81`.`
Case 3:
λ ≠ -1,
1`In this case, from the equations `x(1 + λ) = 0` and `y(λ − 1) = 0`,
we get that either `x = y = 0` or `λ = -1/3`.
If `x = y = 0`, then `x^2 + y^2 = 0`, which is not possible since `x^2 + y^2 = 81`.
So, `λ = -1/3`.
From the equations `x(1 + λ) = 0` and `y(λ − 1) = 0`, we get that either `x = 0` or `y = 0`.
If `x = 0`, then `y = ±9√3`.
If `y = 0`, then `x = ±9√3`.
So, we have four critical points:`
(9√3,0), (-9√3,0), (0,9√3), (0,-9√3)`
Let's evaluate the function at these points:`
f(9√3,0) = 243`
`f(-9√3,0) = 243
``f(0,9√3) = -243
``f(0,-9√3) = -243
`So, the maximum value of `f(x,y)` is `243` and the minimum value is `-243`.
Therefore, the maximum value of the function `f(x,y) = x^2−y^2` subject to the constraint `x^2 + y^2 = 81` is `243` and the minimum value is `-81`.
To know more about function visit:
https://brainly.com/question/30721594
#SPJ11
Which of these angles is the largest angle for which it would be appropriate to use the small angle approximation for cosine?
20 degrees
15 degrees
5 degrees
30 degrees
Answers
The largest angle for which it would be appropriate to use the small angle approximation for cosine is 15 degrees
We know that basic trigonometric identities are the primary trigonometric ratios of sine, cosine, and tangent that are defined in a right triangle but at the same time these ratios have numerous applications, but their most important application is finding unknown sides and angles in a right triangle.
Small Angle approximation can be said to be the approximation that can be used to find a more simplified formula for each of the three primary ratios. This process is called a small-angle approximation or applying the small-angle approximation theorem.
To learn more about small-angle approximation, click here:
brainly.com/question/30387088
#SPJ4
what day of the year does the subsolar ppoint fall on the eqautor
Answers
The subsolar point falls on the equator on two specific days of the year, which are the vernal equinox and the autumnal equinox.
The vernal equinox, also known as the March equinox or the spring equinox, occurs on or around March 20th. The autumnal equinox, also known as the September equinox or the fall equinox, occurs on or around September 22nd. On these two days, the subsolar point is directly over the equator, resulting in nearly equal amounts of daylight and darkness at all latitudes.
In summary, the subsolar point falls on the equator on the vernal equinox (March 20th) and the autumnal equinox (September 22nd).
Learn more about subsolar point :https://brainly.com/question/13020132
#SPJ11
Solve for x please
A)-8
B)-9
C)8
D9

Answers
Answer:
My answer is -9.becasiug
The sum of a number and seven more than the number is 43. What is the number?
Answers
Answer:
18
Step-by-step explanation:
we can use the variable x to represent the number since it's currently unknownseven more than the number can be represented as x + 7we can find the sum of both by adding themx + x + 7 = 43
2x + 7 = 43
-7 -7
2x = 36
we divide by 2 on both sides to isolate xx = 18
The figure below is a net for a right rectangular prism. Its surface area is 416 m² and the area of some of the faces are filled in below. Find the area of the missing faces, and the missing dimension.

Answers
The area of each of the missing faces is 40 m².
The length of each of the missing faces is 10 m.
The missing dimension is 10 m by 4 m.
What is area?Area is the region bounded by a plane shape.
To calculate the area of each missing face, we use the formula below.
Formula:
a = [A-2(48+120)]/2.............. Equation 1Where:
a = Area of each missing facesA = Total surface area of the rectangular prismFrom the question,
Given:
A = 416 m²Substitute these values into equation 1
a = [416-2(48+120)]/2a = (416-336)/2a = 40 m²And the length of each of the missing edge can be calculated using the formula below
Formula:
l = a/w.................Equation 2Where:
l = Length of each of the missing edgew = width of each of the missing edgeFrom the diagram in the question,
Given:
w = 4 ma = 40 m²Substitute into equation 2
l = 40/4l = 10 mHence, the length is 10 m.
Learn more about area here: https://brainly.com/question/25092270
#SPJ1
A pile of 15 boxes is 3 metres high. What is the depth of each box?
5 m
0.002 km
200 cm
200 mm
Answers
ANSWER:
200 millimetre
====================================================
Work Shown:
1 meter = 100 cm
3 meters = 300 cm (multiply both sides by 3)
15 boxes are 300 cm tall combined, so 300/15 = 20 cm is the height of each box.
------------
Unfortunately 20 cm isn't listed as an answer choice, but we can convert to km and see what happens
20 cm * (1 m/100 cm)*(1 km/1000 m) = 20/(100*1000) = 0.0002 km
It's close, but off by a digit. Choice B has two zeros while 0.0002 has three zeros between the decimal point and the '2'.
------------
Let's convert to mm and see what happens
20 cm * (10 mm/1 cm) = 200 mm
Through trial and error, we arrived at the final answer.
