Please help me out, i can not understand this, i will give a brainliest out to whoever can help me

Answers
Related Questions
Isla was researching kiwi birds. She categorized each bird she observed by species and gender. The two-way frequency table below shows data from observations of 200 kiwis.
Which of the following statements is true about the kiwis observed?
(Choice A)
There were the most observations of female tokoeka kiwis.
(Choice B)
Great spotted kiwis were more likely to be male than female.
(Choice C)
More than half of the kiwis were Northland brown kiwis.
(Choice D)
Northland brown kiwis were more likely to be female than tokoeka kiwis were.

Answers
Answer:
A.
I hope it helps
There were the most observations of female tokoeka kiwis in the given frequency table so option (A) will be correct.
What is a frequency table?A frequency table is a list of objects with the frequency of each item shown in the table.
The frequency of an occurrence or a value is the number of times it happens.
Given the frequency table of kiwi birds with their gender.
Number of female tokoeka kiwis = 44
Now if we look at the table there is none of any bird that is greater than 44 which means it is the most observations in the research.
Hence "There were the most observations of female tokoeka kiwis".
To learn more about the frequency table,
brainly.com/question/12576014
#SPJ2
Find the value of x that makes m || n. Explain.

Answers
Answer:
Step-by-step explanation:
x=120/3
x=40
Answer:
40
Step-by-step explanation:
if m||n then 3x must be equal to 120°
120° = 3x divide both sides by 3
40 = x
1. Ben earns $6/h baby sitting. He is saving his earnings to buy an MP3 player that costs $360.
a) Write a relation to show how Ben's savings are related to the number of hours he baby sits
b) Make a table to show the amount of savings after baby sitting for 10, 20, 30, 40, and 50 hours.
c) Draw a graph to show the relation. Describe the graph.
d) Use your graph. How much will Ben have saved after baby sitting for 60h?
Please i need the answer this is Lesson 1.6: Graphing Relations
Answers
B 10=60 20=120 30=180 40=240 50=300
D=360
I need help with this

Answers
The value of the function (f - g)(x) would be \((f-g)(x)=x^2-11x+4\).
Option (A) is correct.
What are composite functions?
A composite function is generally a function that is written inside another function. The composition of a function is done by substituting one function into another function. For example, f [g (x)] is the composite function of f (x) and g (x). The composite function f [g (x)] is read as “f of g of x”.'
Given:
\(f(x)=4x^2-5x\\\\g(x)=3x^2+6x-4\)
Now by using the definition of composite functions we can write,
\((f-g)(x)=f(x)-g(x)\\\\(f-g)(x)=4x^2-5x-(3x^2+6x-4)\\\\(f-g)(x)=4x^2-5x-3x^2-6x+4\\\\(f-g)(x)=x^2-11x+4\)
Hence, the value of the function (f - g)(x) would be \((f-g)(x)=x^2-11x+4\).
To learn more about composite functions, visit:
https://brainly.com/question/10687170
#SPJ1
The function f(x) = -5x² + 20x + 55 models the height of a ball x seconds after it is thrown into the air. What is the total time that the ball is in the air?
Answers
Answer:
The ball is in the air for about 5.873 seconds.
Step-by-step explanation:
The function:
\(f(x)=-5x^2+20x+55\)
Models the height of a ball x seconds after it is thrown in the air.
And we want to find the total time the ball is in the air.
So, we can simply find the time x at which the ball lands. If it lands, its height f above the ground will be 0. Thus:
\(0=-5x^2+20x+55\)
We will solve for x. Dividing both sides by -5 yields:
\(0=x^2-4x-11\)
The equation is unfactorable, so we can use the quadratic formula:
\(\displaystyle x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\)
In this case, a = 1, b = -4, and c = -11. So:
\(\displaystyle x=\frac{-(-4)\pm\sqrt{(-4)^2-4(1)(-11)}}{2(1)}\)
Evaluate:
\(\displaystyle\begin{aligned} x&=\frac{4\pm\sqrt{16+44}}{2}\\&=\frac{4\pm\sqrt{60}}{2}\\&=\frac{4\pm2\sqrt{15}}{2}\\&=2\pm\sqrt{15}\end{aligned}\)
Approximate:
\(x_1=2+\sqrt{15}\approx5.873\text{ or } x_2=2-\sqrt{15}\approx-1.873\)
Since time cannot be negative, our only solution is the first choice.
So, the ball is in the air for about 5.873 seconds.
More math...........

Answers
Answer:
A and C
Step-by-step explanation:
A and C are correct
a 82-ft tree casts a shadow that is 110 ft long. what is the angle of elevation of the sun? (round your answer to one decimal place.)
Answers
The angle of elevation of the sun is, 36.7 degree.
What is angle of elevation?
The angle of elevation is the angle created between the line of sight and the horizontal. The angle created is an angle of elevation if the line of sight is upward from the horizontal line.
Given: A 82-ft tree casts a shadow that is 110 ft long.
So, by using the tangent ratio,
tanθ = 82/110
Apply tan^(-1) on both sides, we get
So, θ = \(tan^-^1(\frac{82}{110} )\)
θ = 36.7 degree.
Therefore, when a 82-ft tree casts a shadow that is 110 ft long, the angle of elevation of the sun is 36.7 degree.
To know more about the angle of elevation, click on the link
https://brainly.com/question/88158
#SPJ4
Can someone please help me with this please

Answers
Answer:
The first is not a function. The second is.
Step-by-step explanation:
See attachment.

Use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bounded by the curves y=x2, y=0, x=1, and x=2 about the line x=4.
Answers
Volume of the solid obtained by rotating the region is 67π/6 .
Given,
Curves:
y=x², y=0, x=1, and x=2 .
The arc of the parabola runs from (1,1) to (2,4) with vertical lines from those points to the x-axis. Rotated around x=4 gives a solid with a missing circular center.
The height of the rectangle is determined by the function, which is x² . The base of the rectangle is the circumference of the circular object that it was wrapped around.
Circumference = 2πr
At first, the distance is from x=1 to x=4, so r=3.
It will diminish until x=2, when r=2.
For any given value of x from 1 to 2, the radius will be 4-x
The circumference at any given value of x,
= 2 * π * (4-x)
The area of the rectangular region is base x height,
= \(\int _1^22\pi \left(4-x\right)x^2dx\)
= \(2\pi \cdot \int _1^2\left(4-x\right)x^2dx\)
= \(2\pi \left(\int _1^24x^2dx-\int _1^2x^3dx\right)\)
= \(2\pi \left(\frac{28}{3}-\frac{15}{4}\right)\)
Therefore volume of the solid is,
= 67π/6
Know more about volume of solids,
https://brainly.com/question/23705404
#SPJ4
when using a graduated pipet, at which point do you measure the volume?
Answers
The volume is measured at the bottom of the meniscus when the liquid level is between the two etched marks on the pipet.
1. Place the graduated pipet on a flat surface and make sure it is level
2. Draw the liquid up until the meniscus is level with the etched line that corresponds to the desired volume
3. Make sure the liquid is not touching the etched line above it
4. Observe the bottom of the meniscus and take the reading at the point where the liquid level is between the two etched lines
The volume is measured at the bottom of the meniscus when the liquid level is between the two etched marks on the pipet.
Learn more about volume here
https://brainly.com/question/16134180
#SPJ4
Given f(x) = (x − 1)(x 2)(x − 3), what are the zeros and end behavior of the function? −1, 2, −3; continues downward to the left and upward to the right −1, 2, −3; continues upward to the left and downward to the right 1, −2, 3; continues downward to the left and upward to the right 1, −2, 3; continues upward to the left and downward to the right
Answers
The end behavior of the function f(x) is: continues downward to the left and upward to the right.
Consider the function,
f(x) = (x + 1)(x - 2)(x + 3)
The zeros are when f(x) = 0
f(x) = 0
(x + 1)(x - 2)(x + 3) = 0
Therefore,
(x + 1) = 0
So, x = -1
(x - 2) = 0
So, x = 2
(x + 3) = 0
So, x = -3
Therefore, the zeros are at x = - 1, x = 2 and x = - 3
To expand the function, we multiply the brackets:
f(x) = (x + 1)(x - 2)(x + 3)
f(x) = ( x + 1 )( x² + x - 6 )
f(x) = x³ + 2x² - 5x - 6
As the leading coefficient (the coefficient of x³) is positive, the end behavior of the function is:
f(x ) → + ∞, as x → + ∞
f(x ) → - ∞, as x → - ∞
Therefore, the end behavior is "continues downward to the left and upward to the right".
Learn more about end behavior here:
brainly.com/question/28156509
#SPJ4
pls help due in an hour if u get it right ill mark you brainliest

Answers
Answer:
The answer is ≈3 to the nearest whole number
Step-by-step explanation:
using SOH CAH TOA
BCA
sin0=opp/hyp
sin0=7.9/11
0=sin‐¹(7.9/11)
0=46 to the nearest degree
<A=<D
so,<EDF=46°
tan0=adj/hyp
tan46=x/3.3
x=tan46×3.3
x=3 to the nearest whole number
-(2x + 5.9) +8.3 = 4+3(-x+ 2.8)
Answers
Answer:
x =10
Step-by-step explanation:
Equation
-(2x + 5.9) +8.3 = 4+3(-x+ 2.8) Carefully remove both sets of brackets
Solution
-2x - 5.9 + 8.3 = 4 + -3x + 8.4 Combine like terms on both sides
-2x + 2.4 = -3x + 12.4 Add 3x to both sides
-2x+3x + 2.4 = -3x+3x + 12.4 Combine
x + 2.4 = 12.4 Subtract 2.4 from both sides
x + 2.4 - 2.4 = 12.4 - 2.4 Combine
x = 10
radius of 4000miles while flying 10miles above the surface. something unusal on the horizon infront of her, how far away is she
Answers
The pilot can see up to a distance of approximately 144 miles from her position. However, it is important to note that this distance may vary based on atmospheric conditions and other factors.
Assuming the earth is a perfect sphere, the radius of the earth is approximately 4000 miles.
If the pilot is flying 10 miles above the surface, then her altitude is 4010 miles.
Now, let's assume that she sees something unusual on the horizon in front of her.
The horizon is the line where the sky appears to meet the earth's surface when you look out into the distance.
It is the farthest distance that you can see because the earth's curvature blocks anything beyond that point.
The distance of the horizon from an observer is directly proportional to the height of the observer above the surface of the earth.
The following formula can be used to calculate the distance of the horizon from an observer:
Distance to horizon = sqrt(2Rh + h^2)where R is the radius of the earth and h is the height of the observer above the surface of the earth.
If we substitute the given values into the formula, we can find the distance of the horizon from the pilot: Distance to horizon = sqrt(2 * 4000 + 10^2)≈ 144.07 miles
For more such questions on atmospheric
https://brainly.com/question/19587559
#SPJ8
what is the answer to x2 = 121.
Answers
Answer:
11 if you mean x^2
Step-by-step explanation:
Since we are solving for x, we need to just get x by its self. The only thing we have to do is get rid of the exponent of (^2). to do this, we have to take teh square root of both sides:
The square root of x^2 is x
The square root of 121 is 11
So the asnwer is x = 11
Step-by-step explanation: A common mistake in this problem would be to say that if x² = 121, x must equal 11.
However, you must set the equation equal to 0 first.
So our first step is to subtract 121 from both sides to get x² - 121 = 0.
Next, factor the left side to get (x + 11)(x - 11) = 0
So either x + 11 = 0 or x - 11 = 0.
Solving each equation from here, we find that x = -11 or x = 11.
So our answer is not just 11, it's {11, -11}.
Which expression represents the number -2i(5- i) + (17- 8i) rewritten in a + bi
form?
O 15-18i
O 15-2i
O 19 - 18i
O 11 + 8i
Answers
Answer:
(a) 15 -18i
Step-by-step explanation:
You want the simplified form of the expression -2i(5- i) + (17- 8i).
Complex numbersFor many purposes, the value i in a complex number can be treated in the same way a variable would be treated. When simplifying an expression involving i, any instances of i² can be replaced with the real value -1.
-2i(5- i) + (17- 8i) = -10i +2i² +17 -8i
= -2 +17 +(-10 -8)i
= 15 -18i
__
Additional comment
Your scientific or graphing calculator can probably help you evaluate such expressions.

CAN SOMEONE HELP ME PLZ!!!

Answers
Answer:
The answer is 4! I hope you do Great!
Step-by-step explanation:
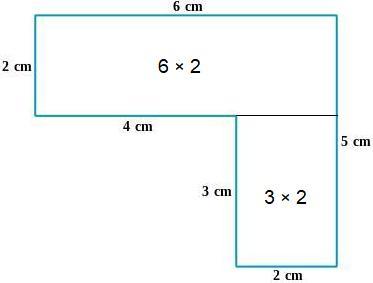
pls help 20 points!!

Answers
Answer:
\(\huge\boxed{\sf 18 cm\²}\)
Step-by-step explanation:
The figure consists of 2 rectangles.
Rectangle 1 Area:
Length = 5 cm
Width = 2 cm
Area = Length * Width
A = 5 * 2
A = 10 cm²
Rectangle 2 Area:
Length = 4 cm
Width = 2 cm
Area = 2 * 4
A = 8 cm²
Area of the whole figure:
= Rectangle 1 + Rectangle 2
= 10 + 8
= 18 cm²
\(\rule[225]{225}{2}\)
Hope this helped!
~AH1807Answer:
\(\Large \boxed{\sf 18 \ cm^2}\)
Step-by-step explanation:
Split shape into two rectangles
Calculate area of the two rectangles and add them
\(6\times 2+3 \times 2=18\)
the two adjacent angles formed when two lines meet or intersect.
so is it vertical liner or complementary angles
Answers
Adjacent angles are a pair of angles that have a similar vertex and side and add up to 180 degrees. Contrarily, complementary angles are two angles that together measure 90 degrees and have a number of mathematical uses.
There are numerous angles created when two lines intersect. When two of these angles are referred to as neighbouring, it signifies that they have a similar vertex and side. A linear pair of angles is any two angles that are next to one another on one side of the intersection.
The sum of two linear angles is 180 degrees. As a result, it is simple to determine the measure of another angle if you know the size of one. Geometry relies on linear pairings of angles to solve problems involving angles and lines, hence they are crucial.
Complementary angles, on the other hand, are two angles that sum up to 90 degrees. Although they are not need to be, they can be adjacent angles. When two angles are parallel to one another, the sum of their respective measures is 90 degrees.
Trigonometry and geometry are two areas of mathematics where complementary angles are helpful. In issues involving right triangles, where one of the angles is always 90 degrees, they are frequently used.
In conclusion, neighbouring angles are a pair of parallel angles that have the same vertex and side and add up to 180 degrees. Contrarily, complementary angles are two angles that together measure 90 degrees and have a number of mathematical uses.
Learn more about angles here:
https://brainly.com/question/28451077
#SPJ1
What is the area of a parallelogram if the coordinates of its vertices are (0, -2), (3, 2), (8, 2), and (5, -2)?
A. 12
B. 15
C. 20
D. 24
I will give 30 and brainliest for a good answer
Answers
Answer:
The answer is 24.
Step-by-step explanation:
I graphed it out, and calculated it and this is what I got. I am terribly sorry if this is wrong. Please forgive, but I think it is right.
Answer:
D
Step-by-step explanation:
x+3y=0 and 12y=-4 equation plz help.
Answers
Answer:
\(x = 1\) and \(y = -\frac{1}{3}\)
Step-by-step explanation:
So we can equate the second equation in terms of y by dividing both sides by 12:
\(y = -\frac{1}{3}\)
Let us substitute this into the first equation:
\(x + 3y = 0\)
then becomes
\(x + 3(-\frac{1}{3} ) = 0\)
which simplifies to
\(x - 1 = 0\)
Finally solving for x gives us:
\(x = 1\)
Therefore, \(x = 1\) and \(y = -\frac{1}{3}\)
Hope this helps!
Brainliest please!
Answer:
x=1, y=-1/3
Step-by-step explanation:
x+3y=0
12y=-4
12y=-4
y=-1/3
x+3y=0
x+3(-1/3)=0
x-1=0
x=1
write the first trigonometric function in terms of the second for in the given quadrant. cos(), sin(); in quadrant iii
Answers
In the third quadrant, the trigonometric function cosine (cos) can be expressed in terms of the trigonometric function sine (sin) using the negative sign. Specifically, in quadrant III, cos(θ) = -√(1 - sin²(θ)).
In the third quadrant, both the x-coordinate and y-coordinate of a point on the unit circle are negative. The cosine of an angle θ in this quadrant is defined as the ratio of the adjacent side to the hypotenuse of a right triangle formed by the angle.
To express cos(θ) in terms of sin(θ), we can use the Pythagorean identity sin²(θ) + cos²(θ) = 1. Solving for cos(θ), we get cos(θ) = √(1 - sin²(θ)). However, since we are in quadrant III where cos(θ) is negative, we introduce a negative sign to obtain cos(θ) = -√(1 - sin²(θ)).
Therefore, in quadrant III, the cosine function can be written in terms of the sine function as cos(θ) = -√(1 - sin²(θ)). This allows us to relate the values of sine and cosine for angles in this particular quadrant.
To learn more about trigonometric function: -brainly.com/question/25618616
#SPJ11
What percentage of young women and teens in the united states is clinically bulimic?
Answers
An eating disorder indicated by binge eating and following purging, usually by induced vomiting or usage of laxatives
1 to 3 percent of female teenagers and youthful adults in the United States exist clinically bulimic.
What are the symptoms of bulimia?Above average body weight.Recurrent episodes of binge eating and fear of not being able to stop eating.Self-induced vomitingExcessive exercise.Excessive fasting.Peculiar eating habits.Inappropriate use of laxatives or diuretics.As numerous as one in ten college women suffer from a clinical or about clinical eating disorder, including 5.1% who sorrow from bulimia nervosa. Around five percent of adolescent and adult women and one percent of men contain anorexia nervosa, bulimia nervosa, or binge eating disorder.
An eating disorder indicated by binge eating and following purging, usually by induced vomiting or usage of laxatives
1 to 3 percent of female teenagers and youthful adults in the United States exist clinically bulimic.
To learn more about bulimia refer to:
https://brainly.com/question/14872551
#SPJ4
What is the conditional probability that a randomly generated bit string of length four contains at least two consecutive 0s, given that the first bit is a 1?.
Answers
The conditional probability is 0.25.
To calculate the conditional probability, we need to find the probability that a randomly generated bit string of length four contains at least two consecutive 0s, given that the first bit is a 1.
Let's consider the possible bit strings of length four that start with 1:
1xxx (where x can be 0 or 1)
There are two possibilities for the first bit (1 or 0), and for each of these possibilities, there are two possibilities for each of the remaining three bits (0 or 1).
Now, let's find the bit strings that contain at least two consecutive 0s:
1xxx (where x is 0)
1000
1010
1100
1110
Out of the possible 1xxx bit strings, there are four that contain at least two consecutive 0s.
Now, the conditional probability is calculated as the probability of the event (bit string contains at least two consecutive 0s) given the condition (first bit is 1).
Conditional Probability = (Number of favorable outcomes) / (Total number of possible outcomes)
Conditional Probability = 4 / (2 * 2 * 2 * 2) = 4 / 16 = 1/4 = 0.25
So, the conditional probability that a randomly generated bit string of length four contains at least two consecutive 0s, given that the first bit is a 1, is 0.25 or 25%.
To learn more about probability here:
https://brainly.com/question/31828911
#SPJ4
Five years ago, a father was 3 times as old
as his son, now their combined ages amount
to 110 years. How old are they?
Answers
Answer:
Father is 80 years old and the son is 30
Step-by-step explanation:
Let father be x and son be y:
x-5 = 3(y-5)
x = 3y-10 ------ eq1
x+y = 110
x = 110 -y -------- eq2
Now if we combine the 2 equations we get:
3y + y = 110+10
y=30 (sons age)
Substituting in equation 2 we get:
x = 110 - 30
x = 80
Therefore, the fathers age is 80 and the sons age is 30.
Find the volume for 2 different spheres by randomly choosing different radii.
Using the same radii values, find the volume of 2 cylinders where the height of the cylinder is the same as the diameter of the sphere.
Answers
Answer:
The volume of a sphere of radius r is:
S = (4/3)*pi*r^3
The volume of a cylinder of radius r and height h is:
C = pi*r^2*h
For this problem the height of the cylinders will be equal to the diameter of the spheres, which is equal to two times the radius.
First, let's use the radius: r = 2.
The volume of the sphere will be:
S = (4/3)*3.14*(2)^3 = 33.49
The volume of the cylinder, where h = 2*2 = 4, is:
C = 3.14*(2^2)*4 = 50.24
Now, let's choose the radius r = 3.
The volume of the sphere will be:
S = (4/3)*3.14*3^3 = 113.04
The volume of a cylinder with this radius and h = 3*2 = 6, is:
C = 3.14*(3^2)*6 = 169.56
find the missing numbers in the following equal ratios:
\(\frac{?}{3} = \frac{?}{6} = \frac{8}{?} = \frac{16}{24}\)
Answers
First blank: Dividing the numerator and denominator of 16/24 by 8 gives the unknown to be 2.
Second blank: Dividing the numerator and denominator of 16/24 by 4 gives the unknown to be 4.
Third blank: Dividing the numerator and denominator of 16/24 by 2 gives the unknown to be 12.
Diana uses a wheelbarrow to haul wood from her backyard to the back of her
neighbor's house, located 30 024 feet away. She can push the wheelbarrow
3336 feet before she has to take a break.
How far would she be after 7 breaks?
Answers
I also need help with 1,000,000 in exponential form , 10x10 , and 10,000 x10 please
Answers
Answer:
Step-by-step explanation:
To convert the value 1,000,000 to an exponential form means we are to write the value in multiples of 10. Breaking down the values in multiples of 10 will give;
1,000,000 = 10 * 10 * 10 * 10 * 10 * 10 (it is broken down into 6 places because the value contains 6 zeros)
Express in exponential form
1,000,000 = (10 * 10 * 10) * (10 * 10 * 10)
1,000,000 = (10³) * (10³)
1,000,000 = 10³⁺³
1,000,000 = 10⁶
Hence the value 1,000,000 in exponential form is expressed as 1 * 10⁶
For 10 * 10:
10 * 10 = 10¹ * 10¹
10 * 10 = 10¹⁺¹
10 * 10 = 10²
10 * 10 = 1 * 10²
The value of the expression 10*10 in exponential form is 1 * 10²
For 10,000 * 10:
10,000 * 10 = (10*10*10*10) * 10
10,000 * 10 = (10⁴) * 10¹
10,000 * 10 = 10⁴⁺¹
10,000 * 10 = 1 * 10⁵
Hence, The value of the expression 10000*10 in exponential form is 1 * 10⁵
The graph of f(x) a trigonometric function in the graph of GFX equals C intersect at n points over the interval zero is less than or equal to X less than or equal to two pi there are M algebraic solutions to the equation f(x) equals G of X or M is greater than N which of the following functions is most likely to be f(x)
Answers
the most likely function for f(x) would be one that has multiple roots and intersects the graph of G(x) at n points.
Why it is?
Since f(x) is a trigonometric function and intersects the graph of G(x) at n points over the interval 0 ≤ x ≤ 2π, we can infer that f(x) has n roots or solutions over this interval. Furthermore, if there are M algebraic solutions to the equation f(x) = G(x), then M is greater than n, indicating that there are more solutions beyond the intersection points.
Based on this information, the most likely function for f(x) would be one that has multiple roots and intersects the graph of G(x) at n points. Some examples of trigonometric functions that fit this description include sine, cosine, and tangent functions.
Of these, the sine function would be the most likely candidate since it intersects the x-axis (where G(x) = C) at n points over the interval 0 ≤ x ≤ 2π, and has an infinite number of roots beyond these intersection points. The cosine function would also have n intersections with the x-axis, but it has a different number of roots beyond these points, depending on the phase shift of the function.
The tangent function has vertical asymptotes that can limit the number of intersections with G(x) at C, making it less likely to be f(x).
To know more about Graph related questions visit:
https://brainly.com/question/17267403
#SPJ1
Answer: C. f(x) = cos^2x + cos x
Step-by-step explanation:
Pearson Practice 3.6.9