Answers
The rest of the question is the attached figure
The percent change =
If (+ve) increase and if (-ve) decrease
Part A: What is the percent of change in the cost of a pizza?
The initial price = $7.5
The final price = $9
The percent change = %
Part B: What is the percent of change in the cost of a cheeseburger?
The initial price = $5
The final price = $6.5
The percent change = %
Part C: What is the percent of change in the cost of a serving fries?
The initial price = $2
The final price = $4.5
The percent change = %
Part D: What is the percent of change in the cost of a hot dog?
The initial price = $2.5
The final price = $2
The percent change = %
i found this online i hope if helps you

Step-by-step explanation:
\(\frac{9.00 - 7.50}{7.50} \times 100\% = 20\% \: increase\)\( \frac{6.50 - 5.00}{5.00} \times 100\% = 30\% \: increase\)\( \frac{4.50 - 2.00}{2.00} \times 100\% = 125\% \: increase\)\( \frac{2.00 - 2.50}{2.50} \times 100\% = - 20\%\)In order to get the increase or decrease, we need to get the difference of the two prices first. Then, pick a "reference year".
From the calculations, notice how I made the earlier years as my reference points. If the calculations produced positive results, therefore, it has increased. If it produced a negative results, from the reference year's price, it has decreased in price.
Related Questions
What rule can be used to find the next term of the arithmetic sequence? 39, 60, 81, 102, 123, . .A. an = an–1 – 39B. an = an–1 – 21C. an = an–1 + 21D. an = an–1 + 39the next term of the arithmetic sequence 39, 60, 81, 102, 123, . . . is______.
Answers
The next term of the arithmetic sequence 39, 60, 81, 102, 123, . . . is given by the rule 18 + 21T, where T is any natural number.
An arithmetic sequence is the series where the difference between any two terms is given to be constant.
Here the given arithmetic sequence is,
39, 60, 81, 102, 123, . . .
First term = a = 39
Common Difference = d = 60 - 39 = 21
So, next term,
= 6 th term
= 5 th term + Common Difference
= 123 + 21
= 144
For, any term,
Tth Term = first term + (T-1)Common difference.
Tth Term = 39 + (T-1)21
Tth Term = 39 + 21T - 21
Tth Term = 18 + 21T
So, the rule is 18 + 21T.
To know more about arithmetic sequence, visit,
https://brainly.com/question/6561461
#SPJ4
Answer: first answer is C second answer is 144
Step-by-step explanation:
edge 2023
there are some people on a train
18 get off at the first stop and 21 people get on the train
now there are 65 people on the train
how many were on the train to begin with
Answers
======================================================
Explanation:
18 people get off, and 21 get on
We can write the 18 as -18 to indicate a loss of 18 people. The 21 as +21 to mean we gained 21 people.
The net change is -18+21 = +3 or simply 3.
After the first stop, 3 more people are on the train compared to before reaching this stop.
If x is the number of people before the stop, then x+3 is the number of people after the stop. Set this equal to 65 and solve for x.
x+3 = 65
x = 65-3
x = 62 people were on the train to begin with.
-----------
Check:
62 people to start off
62-18 = 44 people after the 18 people get off
44+21 = 65 people after the 21 new people get on
The answer is confirmed.
A right square pyramid has an altitude of 10 and each side of the base is 6. To the nearest tenth of a centimeter, what is the distance from the apex, or top of the pyramid, to each vertex of the base?.
Answers
We need to use the properties of Pyramid and Right Angled Triangle in this question. The distance from apex to each vertex is 10.9.
How can we solve questions of pyramid?
A three-dimensional figure is a pyramid. Its base is a flat polygon. The remaining faces are all triangles and are referred to as lateral faces. The number of sides on its base is equal to the number of lateral faces. The line segments that two faces intersect to form its edges. The intersection of three or more edges forms a vertex. All the faces, with the exception of the base, join at the apex, a vertex at the top. The base's shape is given by the apex, which is located in opposition to it. In the right pyramid, the apex is precisely over the center of the base. The center of the base will be where a perpendicular line from the apex to the base intersects.
CalculationSo in the question they mentioned Altitude=10 and Base =6.
So using pythagorean theorem,
x2=y2+(10)2-eq1
with y half of the length of the diagonal of the base.
2y=length of the diagnol
and (2y)2 = 72
⇒4y2=72
∴y = 3√2.
So substitute y in eq1 and get x.
⇒ ( 3√2)2+(10)2=(x)2
⇒(x)2=118
∴x=10.86.
x≈10.9
We need to use the properties of Pyramid and Right Angled Triangle in this question. The distance from apex to each vertex is 10.9.
To refer more about Pyramid and Right Angled Triangle , visit:
https://brainly.com/question/15976178
#SPJ1
pls help this is due soon

Answers
Answer:
1/2^4
Step-by-step explanation:
gravel is being dumped from a conveyor belt at a rate of 20 ft3/min, and its coarseness is such that it forms a pile in the shape of a cone whose base diameter and height are always equal. how fast (in ft/min) is the height of the pile increasing when the pile is 11 ft high? (round your answer to two decimal places.)
Answers
Answer:
0.21ft/min
Step-by-step explanation:
\(\sf Volume \ at \ given \ time = \dfrac{dV}{dt}= 20 \ cubic \ feet /min\)
h = d
h = 2r
\(\sf r = \dfrac{h}{2}\)
Volume of heap = (1/3) πr²h
\(\sf V =\dfrac{1}{3}\pi r^2h\\\\V =\dfrac{1}{3}\pi (\frac{h}{2})^2h\\\\V =\dfrac{1}{3}\pi \dfrac{h^2}{4}*h\\\\V=\dfrac{1}{12}\pi h^3\)
Take derivative w.r.t time,
\(\sf \dfrac{dV}{dt}=\dfrac{1}{12}\pi * 3h^2 \dfrac{dh}{dt}\)
h = 11 ft
\(\sf 20 = \dfrac{1}{12}\pi *3*11*11*\dfrac{dh}{dt}\\\\20=\dfrac{121}{4}\pi \dfrac{dh}{dt}\\\\\)
\(\sf \dfrac{20*4}{121*\pi }=\dfrac{dh}{dt}\\\\ \dfrac{80}{120*3.14}=\dfrac{dh}{dt}\)
\(\sf \dfrac{dh}{dt}=0.21\)
The height is increasing at the rate of 0.21 ft/min
what are the possible values for (randgen.nextint(9) -4)? assume a random number generator object named randgen exists. question 35 options: -4...4 -9...9 0...4 0...9
Answers
The correct option would be -4...4.
How to find the range of possible values for the expression (randgen.nextInt(9) - 4)?The expression (randgen.nextInt(9) - 4) uses a random number generator object named randgen to generate a random integer between 0 (inclusive) and 9 (exclusive) using the nextInt() method.
By subtracting 4 from this random integer, we determine the range of possible values for the expression.
Since the original random integer ranges from 0 to 8, subtracting 4 shifts the range to -4 to 4. This means that the possible values for (randgen.nextInt(9) - 4) can be any integer between -4 and 4, inclusive.
In other words, the expression can yield values such as -4, -3, -2, -1, 0, 1, 2, 3, and 4. These values cover a total of nine integers, including both positive and negative numbers.
Therefore, the correct option is -4...4, which represents the range of possible values for the expression (randgen.nextInt(9) - 4).
Learn more about random integer
brainly.com/question/31474611
#SPJ11
Vicky is an airline attendant. Last week, she worked on flights on 3 small jets and 5 large jets, which could seat a total of 560 passengers. The week before, she was assigned to flights on 5 small jets and 2 large jets, which could seat a total of 338 passengers. How many seats were on each type of flight?
Answers
The number of the small seats is 30 while the number of the big seats is 94.
What is the number of seats on each of the flights?We know that from the question, Vicky is an airline attendant. Last week, she worked on flights on 3 small jets and 5 large jets, which could seat a total of 560 passengers. The week before, she was assigned to flights on 5 small jets and 2 large jets, which could seat a total of 338 passengers.
Now;
Let the number of small seats be x and the number of large seats be y
It follows that;
3x + 5y = 560 ----- (1)
5x + 2y = 338 ------(2)
If you multiply (1) by 5 and (2) by 3 we have;
15x + 25y = 2800 ------ (3)
15x + 6y = 1014 -----------(4)
19 y = 1786
y = 1786/19
= 94
Substitute y = 94 into (1)
3x + 5(94) = 560
x = 560 - 5(94)/3
x = 30
Learn more about simultaneous equations:https://brainly.com/question/16763389
#SPJ1
use the appropriate functions to find the population mean and population standard deviation of the ba (batting average) column. you must handwrite or type the entire function equations (including the equal signs, the function names, and the arguments) and the answers. no credit will be given without the entire equations and the answers. (.1 for mean, .1 for population standard deviation)
Answers
The population mean of the ba column is calculated using the equation μ = Σ(x) / N, while the population standard deviation is found using the equation σ = √[Σ((x-μ)^2) / N].
To find the population mean of the batting average (ba) column, we can use the following equation:
μ = Σ(x) / N
where:
- μ represents the population mean,
- Σ(x) denotes the sum of all values in the ba column, and
- N represents the total number of data points in the ba column.
The population mean of the ba column is μ = Σ(x) / N.
To calculate the population standard deviation of the batting average (ba) column, we can utilize the following equation:
σ = √[Σ((x-μ)^2) / N]
where:
- σ represents the population standard deviation,
- Σ((x-μ)^2) denotes the sum of the squared differences between each data point and the population mean (μ), and
- N represents the total number of data points in the ba column.
The population standard deviation of the ba column is σ = √[Σ((x-μ)^2) / N].
In summary, the population mean of the ba column is calculated using the equation μ = Σ(x) / N, while the population standard deviation is found using the equation σ = √[Σ((x-μ)^2) / N].
Learn more about population mean here
https://brainly.com/question/31101410
#SPJ11
Everett bought a hat and a shirt that were both on sale. The hat was on sale for 2/5 off the original price, and the shirt was on sale for 1/10 off the original price. How much more was the discount on the hat than the discount on the shirt?
Answers
Answer: 3/10
Step-by-step explanation:
Hat price 3/5
Shirt price 9/10
Difference in Discount 2/5 - 1/10 = 4/10 - 1/10
Solve for y
2(y + 2) = 62(y+2)=6
Answers
Answer:
y=-8
Step-by-step explanation:
2y+4=62y+124=6
2y-62y=124-4=6
-60y=120=6
divide both side by -60
y=120/-60=6
y=-2=6
y=-2-6
y=-8
A function u(x, t) is sought that satisfies the Example 5.7.5 (Heat equation partial differential equation (PDE) du(x, t) ² u(x, t) 0 0, " ət 0x² and which satisfies the boundary conditions u(0, t) = 0, u(1, t) = 0 for t>0, and the initial value condition u(x,0) = 3 sin(2x) for 0≤x≤ 1. 02U(x,s) 0х2 — sU(x,s) = -3sin(2лх).
Answers
The specific solution that satisfies all the given conditions is:
u(x, t) = (3/π) sin(2x) \(e^{(-4\pi^2t)}\)
To find the function u(x, t) that satisfies the given heat equation partial differential equation (PDE), boundary conditions, and initial value condition, we can use the method of separation of variables.
Let's start by assuming that u(x, t) can be represented as a product of two functions: X(x) and T(t).
u(x, t) = X(x)T(t)
Substituting this into the heat equation PDE, we have:
X(x)T'(t) = kX''(x)T(t)
Dividing both sides by kX(x)T(t), we get:
T'(t) / T(t) = kX''(x) / X(x)
Since the left side only depends on t and the right side only depends on x, they must be equal to a constant value, which we'll denote as -λ².
T'(t) / T(t) = -λ²
X''(x) / X(x) = -λ²
Now we have two ordinary differential equations:
T'(t) + λ²T(t) = 0
X''(x) + λ²X(x) = 0
Solving the first equation for T(t), we find:
T(t) = C\(e^{(-\lambda^2t)}\)
Next, we solve the second equation for X(x). The boundary conditions u(0, t) = 0 and u(1, t) = 0 suggest that X(0) = 0 and X(1) = 0.
The general solution to X''(x) + λ²X(x) = 0 is:
X(x) = A sin(λx) + B cos(λx)
Applying the boundary conditions, we have:
X(0) = A sin(0) + B cos(0) = B = 0
X(1) = A sin(λ) = 0
To satisfy the condition X(1) = 0, we must have A sin(λ) = 0. Since we want a non-trivial solution, A cannot be zero. Therefore, sin(λ) = 0, which implies λ = nπ for n = 1, 2, 3, ...
The eigenfunctions \(X_n(x)\) corresponding to the eigenvalues \(\lambda_n = n\pi\) are:
\(X_n(x) = A_n sin(n\pi x)\)
Putting everything together, the general solution to the heat equation PDE with the given boundary conditions and initial value condition is:
u(x, t) = ∑\([A_n sin(n\pi x) e^{(-n^2\pi^2t)}]\)
To find the specific solution that satisfies the initial value condition u(x, 0) = 3 sin(2x), we can use the Fourier sine series expansion. Comparing this expansion to the general solution, we can determine the coefficients \(A_n\).
u(x, 0) = ∑[\(A_n\) sin(nπx)] = 3 sin(2x)
From the Fourier sine series, we can identify that \(A_2\) = 3/π. All other \(A_n\) coefficients are zero.
Therefore, the specific solution that satisfies all the given conditions is:
u(x, t) = (3/π) sin(2x) \(e^{(-4\pi^2t)\)
This function u(x, t) satisfies the heat equation PDE, the boundary conditions u(0, t) = 0, u(1, t) = 0, and the initial value condition u(x, 0) = 3 sin(2x) for 0 ≤ x ≤ 1.
To learn more about Fourier sine visit:
brainly.com/question/32261876
#SPJ11
PQRS is a parallelogram. If mQRS = (9x - 20)° and
mSPQ = (4x + 90)°, what is the value of x?
22
8.5
14
10
Answers
Answer:
x = 8.5
Step-by-step explanation:
In this question, we are to calculate the value of x.
To calculate this, we shall be utilizing one of the important properties of parallelogram.
This property is that opposite angles of a parallelogram are equal.
This means that mQSR = mSPQ = 4x + 90
Now to finally calculate x, we make use of another important parallelogram property which is that angles of parallelogram which faces each other are supplementary.
This means that they add up to be 180
Since mQSR faces mQRS
This means that;
4x + 90 + 9x -20 = 180
13x + 70 = 180
13x = 110
x = 110/13 which is approximately 8.5

Find the global min and max of the function f(x, y) = 3y - 2x², on the region bounded by y = x²+x-1 and the line y=x. 6
Answers
The global min and max of the function f(x, y) = 3y - 2x², on the region bounded is global maximum value is 1,
Given the function f(x, y) = 3y - 2x².
The region is bounded by the line y=x and the parabola y = x² + x - 1.
Therefore, the extreme values of the function f(x, y) = 3y - 2x² are either on the boundary of the region or at critical points inside the region. Let's start by finding the boundary points for this problem.
Boundary Points: We know that the region is bounded by y = x²+x-1 and y = x. Setting the two equations equal to each other to find their intersection points, we have:x² + x - 1 = x.
Rearranging the equation, we get:x² - 1 = 0. Solving for x, we have:x = ±1.Now, plugging these values into y = x, we get two boundary points, which are: (1, 1) and (-1, -1).
Let's evaluate f(x, y) = 3y - 2x² at these two points to find the maximum and minimum values:
At (1, 1):f(1, 1) = 3(1) - 2(1)² = 1.At (-1, -1):f(-1, -1) = 3(-1) - 2(-1)² = -1.
Therefore, the global maximum value is 1, which occurs at (1, 1), and the global minimum value is -1, which occurs at (-1, -1).
Hence, the global min and max of the function f(x, y) = 3y - 2x², on the region bounded by y = x²+x-1 and the line y=x is global maximum value is 1, which occurs at (1, 1), and the global minimum value is -1, which occurs at (-1, -1).
Know more about the global maximum
https://brainly.com/question/13602432
#SPJ11
What is the solution to this equation?
- 4
A. Y = 4
B. X= 8
C. X= 2
D. X= 16

Answers
Answer:
The correct answer is C. X= 2
15. Find the effective annual rate if $5000 is deposited at 3% annual interest, compounded continuously. 16. Joe's Bank has an investment account that pays 2% interest per annum, compounded continuously. World Bank has an investment account that pays 4% interest per annum, compounded quarterly. If you were to invest $1,000 into an account for 1 year, which one would you choose? What about 30 years?
Answers
To find the annual rate,
15. Depositing $5000 at 3% annual interest, compounded continuously, results in an effective annual rate of approximately 3.05%.
16. For a $1000 investment, Joe's Bank is better for both 1 year ($1020.20) and 30 years ($1822.12) compared to World Bank ($1040.60 and $2208.04).
From the provided data,
15. To find the effective annual rate when $5000 is deposited at 3% annual interest, compounded continuously, we can use the formula for continuous compounding:
A = P * e^(rt)
Where:
A = Final amount
P = Principal amount
r = Annual interest rate (in decimal form)
t = Time in years
e = Euler's number (approximately 2.71828)
In this case, P = $5000, r = 0.03, and t = 1. Plugging in these values:
A = 5000 * e^(0.03*1)
A ≈ 5000 * e^0.03
A ≈ 5000 * 1.030454
A ≈ $5152.27
To find the effective annual rate, let us find the interest amount,
Interest amount = Final amount - Principal amount = 5152.27 - 5000 = 152. 27
Effective interest rate = (152.27/5000) * 100 = 3.05%
Therefore, the effective annual rate when $5000 is deposited at 3% annual interest, compounded continuously, is approximately 3.05%.
16. To determine which investment account to choose, let's calculate the future value of $1000 invested for 1 year and 30 years in each account.
Joe's Bank:A = P * e^(rt)
A = 1000 * e^(0.02*1)
A ≈ 1000 * e^0.02
A ≈ 1000 * 1.020201
A ≈ $1020.20 (1 year)
A = 1000 * e^(0.02*30)
A ≈ 1000 * e^0.6
A ≈ 1000 * 1.822119
A ≈ $1822.12 (30 years)
World Bank:A = P * (1 + r/n)^(nt)
A = 1000 * (1 + 0.04/4)^(4*1)
A ≈ 1000 * (1 + 0.01)^4
A ≈ 1000 * 1.040604
A ≈ $1040.60 (1 year)
A = 1000 * (1 + 0.04/4)^(4*30)
A ≈ 1000 * (1 + 0.01)^120
A ≈ 1000 * 3.300387
A ≈ $3300.387 (30 years)
Therefore, if you were to invest $1000 for 1 year, Joe's Bank would yield approximately $1020.20 while the World Bank would yield approximately $1040.60. Hence, the World Bank account would be the better choice.
However, if the investment is for 30 years, Joe's Bank would accumulate approximately $1822.12, whereas the World Bank would accumulate approximately $2208.04. In this case, the World Bank account would be the better choice as well.
To learn more about compound interest visit:
https://brainly.com/question/3989769
#SPJ11
A soccer player takes a shot on goal 15 times and scores a goal 3 of those attempts. What are the odds of the soccer player scoring a goal?
a. 3/12
b. 4
c. 3/15
d. 5
Answers
The odds of the soccer player scoring a goal is 4. The correct option is (b).
The odds of an event happening can be calculated by dividing the number of successful outcomes by the number of unsuccessful outcomes.
In this case, the soccer player scored a goal 3 times out of 15 attempts.
The number of successful outcomes is 3 (goals scored), and the number of unsuccessful outcomes is 15 - 3 = 12 (failed attempts).
Therefore, the odds of the soccer player scoring a goal can be expressed as 3:12, which can be simplified to 1:4.
To match the given answer choices, we can rewrite the odds as a fraction by dividing both sides by the number of successful outcomes:
Odds = Successful outcomes : Unsuccessful outcomes
Odds = 3 : 12
Odds = 3/3 : 12/3
Odds = 1 : 4
So, the correct answer is option b. 4.
To know more about odds refer here:
https://brainly.com/question/30315635#
#SPJ11
The hydrogen ion concentration, [H^+], in a certain cleaning compound is [H^+] = 3.7 times 10^-10. Use the formula pH = - log [H^+] to find the pH of the cleaning compound. The pH is approximately.
Answers
The pH of the cleaning compound is found to be approximately 9.43.
The hydrogen ion concentration, [H+], in a certain cleaning compound is [H+] = 3.7 times 10⁻¹⁰
We will use the formula pH = - log [H+] to find the pH of the cleaning compound.
Acidic and basic compounds are measured on the pH scale, which ranges from 0 to 14.
A pH of 7 is considered neutral, a pH less than 7 is acidic, and a pH greater than 7 is basic.
The lower the pH, the more acidic the compound, and the higher the pH, the more basic the compound.
pH = - log [H+]
We can substitute the given hydrogen ion concentration value in the above formula to obtain the pH of the cleaning compound.
pH = - log 3.7 × 10⁻¹⁰
pH = - (- 9.43)
pH = 9.43
Therefore, the pH of the cleaning compound is approximately 9.43.
Note: 1. When finding the pH value using the formula, we should remember to put the hydrogen ion concentration in brackets "[ ]" and use the base 10 logarithm.
2. We need to keep the significant figures when reporting the final answer. Here, the pH value is given up to two decimal places, so we also need to round off our answer to two decimal places.
Know more about the pH value
https://brainly.com/question/172153
#SPJ11
A tub of water is emptied at a rate of 3 gallons per minute. The equation y –12 = –3(x – 1) models the amount of water remaining, where x is time (in minutes) and y is the amount of water left (in gallons). Analyze the work shown below to determine the initial amount of water.
1. Solve for the y-variable.
y – 12 = –3(x – 1)
y – 12 = –3x + 3
y = –3x +15
2. Write the equation using function notation.
f(x) = –3x +15
The tub started wth how much water?
Answers
Answer:
15 gallons
Step-by-step explanation:
in the _____ theory of interpersonal relationship satisfaction, you would feel happiest in relationships when you feel that the rewards of the relationship equal or exceed its costs.
Answers
The Social Exchange Theory of interpersonal relationship satisfaction suggests that individuals are motivated to stay in a relationship as long as they feel that the rewards of the relationship are greater than the costs.
In the Social Exchange Theory of interpersonal relationship satisfaction, you would feel happiest in relationships when you feel that the rewards of the relationship equal or exceed its costs.
The Social Exchange Theory states that people evaluate their relationships in economic terms, with rewards being the benefits of the relationship and costs being the negatives. Rewards can include affection, attention, emotional support, sex, and companionship. Costs can include time, effort, money, and negative emotions such as stress, anxiety, and sadness.
According to the theory, individuals will be motivated to stay in a relationship as long as they feel that the rewards of the relationship are greater than the costs.
The opposite is also true; if individuals feel that the costs of the relationship are greater than the rewards, they will be motivated to leave the relationship.
Therefore, people are constantly evaluating their relationships to determine whether they are getting what they need from the relationship and whether it is worth continuing.
The Social Exchange Theory of interpersonal relationship satisfaction suggests that individuals are motivated to stay in a relationship as long as they feel that the rewards of the relationship are greater than the costs.
Learn more about costs here:
https://brainly.com/question/28778430
#SPJ11
8th grade math
Write an equation that models each situation in slope-intercept form by finding the slope and y-intercept
Emma started with some money from her birthday and then saved the same amount from her allowance each week. After 4 weeks of saving, Emma had $32. After 8 weeks of saving she has $42.
Answers
Answer:
y = 2.5x + 22
Step-by-step explanation:
the two points are (4,32) and (8,42)
The slope would be
\(\frac{42 - 32}{8-4}\) = \(\frac{10}{4}\) = \(\frac{5}{2}\) = 2.5
This is the slope. She saves $2.50 per week.
the y-intercept is how much money she started with
Use one point. I will us (4,32) and the slope (2.5)
y = 32
m = 2.5
x = 4
y = mx + b
32 = 2.5(4) + b
32 = 10 + b Subtract 10 from both sides
22 = b
This is the y-intercept. This is how much money she had in the beginning.
y =mx + b
y = 2.5x + 22
Line a passes through points (9, 6) and (2, 10). Line b passes through points (2, 11) and (9, 7). Are line a and line b parallel or perpendicular?
Answers
Answer: Parallel
Step-by-step explanation:
We can find their slopes to determine if the lines are parallel or perpendicular.
\(m_a=\frac{10-6}{2-9}=-\frac{4}{7}\\\\m_b=\frac{11-7}{2-9}=-\frac{4}{7}\)
Since the equations of the lines are not the same but the slopes of the lines are equal, they are parallel.
A 2-column table with 5 rows. Column 1 has entries 25 percent, 25 percent, 25 percent, 25 percent, total 100 percent. Column 2 has entries 40 dollars, 40 dollars, 40 dollars, 40 dollars, blank total.
Daniel is a singer, and he promises his agent that he will give him a 25% commission based on what he makes from a show. After paying the agent, Daniel takes home $120. Use the diagram to answer the following questions.
Daniel’s agent made
.
Daniel and the agent made a total of
from the show.
Answers
Answer:
Amount in Blank total = $160
Amount of money Daniel’s agent made = $40
Amount of money Daniel and the agent made
from the show = $160
Step-by-step explanation:
this question is based on the calculation of percentages
so,
it is is given in the question that -
Daniel is a singer, and he promises his agent that he will give him a 25% commission based on what he makes from a show.
After paying the agent, Daniel takes home = $120
so,
let 'x' is the total amount of money that Daniel earned form the show
it is also given that Daniel promised to give 25 % to his agent from what he earned from the show
so, percentage of money left to the Daniel is
100-25 = 75%
therefore according to the question,
75percent of the x = $120
75/100×(x) = 120
3/4×(x) = 120
3x = 120×4
3x = 480
x = $160
so the total amount of money Daniel earned from the show is $160
Now we know that Daniel’s agent made 25% of the total amount of money earned from the show
therefore
25percent of 160 = Daniel’s agent made
25/100 ×160 = Daniel’s agent made
$40 = Daniel’s agent made
so the amount of money earned by Daniel’s agent made is $40
learn more about percentage questions at
https://brainly.com/question/24159063
#SPJ10
Answer: Daniel’s agent made
✔ $40
Daniel and the agent made a total of
✔ $160
from the show.
.
Step-by-step explanation:
Figure ABCD is a rhombus. Rhombus A B C D is shown. Angle A is (5 x 25) degrees and angle D is (7 x minus 1) degrees. What is the value of x
Answers
Answer: 18
Step-by-step explanation:
Opposite angles of a rhombus are congruent, so
\(5 \times 25=7x-1\\\\125=7x-1\\\\126=7x\\\\x=18\)
When a number is written using a whole number plus a portion of one, with the portion separated from the whole number by a dot, is called a __________________.
Answers
Answer:
When a number is written using a whole number plus a portion of one, with the portion separated from the whole number by a dot, is called a mixed fraction.
Step-by-step explanation:
A fraction is a number that is obtained by dividing an integer into equal parts and is expressed as:
\(\frac{numerator}{denominator}\)
An improper fraction is a fraction in which the numerator, that is, the top number, is greater than or equal to the denominator, that is, the bottom number. In contrast, in proper fractions, the numerator is less than the denominator.
Improper fractions can be represented as mixed fractions. A mixed fraction represents a whole number and a proper fraction, in other words, it corresponds to the sum of a whole part plus a fractional part. In summary, mixed fractions are made up of an integer part and a fractional part.
So, when a number is written using a whole number plus a portion of one, with the portion separated from the whole number by a dot, is called a mixed fraction.
Please help fill in this chart

Answers
The point where marginal cost equals $15 is at the production of the 7th pizza. Therefore, the firm should produce 7 pizzas.
What is the firm's shut-down price?The firm's shut-down price is the price at which the firm is indifferent between producing and shutting down.
Using the table provided, we can calculate the missing values:
Variable Cost:
For 0 pizzas, the variable cost is $0.
For 1 pizza, the variable cost is $10.
For 2 pizzas, the variable cost is $12.
For 3 pizzas, the variable cost is $2.
For 4 pizzas, the variable cost is $1.
For 5 pizzas, the variable cost is $2.
For 6 pizzas, the variable cost is $3.
For 7 pizzas, the variable cost is $13.
For 8 pizzas, the variable cost is $16.
For 9 pizzas, the variable cost is $3.
For 10 pizzas, the variable cost is $6.
For 11 pizzas, the variable cost is $4.
Total Cost: To calculate the total cost, we simply add the variable cost and the fixed cost for each level of output. The fixed cost is not given in the table, so we cannot calculate the total cost.
Average Variable Cost:
To calculate the average variable cost, we divide the variable cost by the level of output. For example, the average variable cost for 1 pizza is $10/1 = $10.
Average Fixed Cost:To calculate the average fixed cost, we divide the fixed cost by the level of output.
Average Total Cost: To calculate the average total cost, we add the average variable cost and the average fixed cost. The firm should produce pizzas up to the point where marginal cost equals marginal revenue.
This is the point where the firm maximizes its profit. From the table, we can see that the marginal cost is increasing as output increases, while the marginal revenue remains constant at $15.
Learn more about variable cost at:
brainly.com/question/26373444
#SPJ1
HELP ME ASAPPPPPPPPPPP!!!!!!!!!!!!!
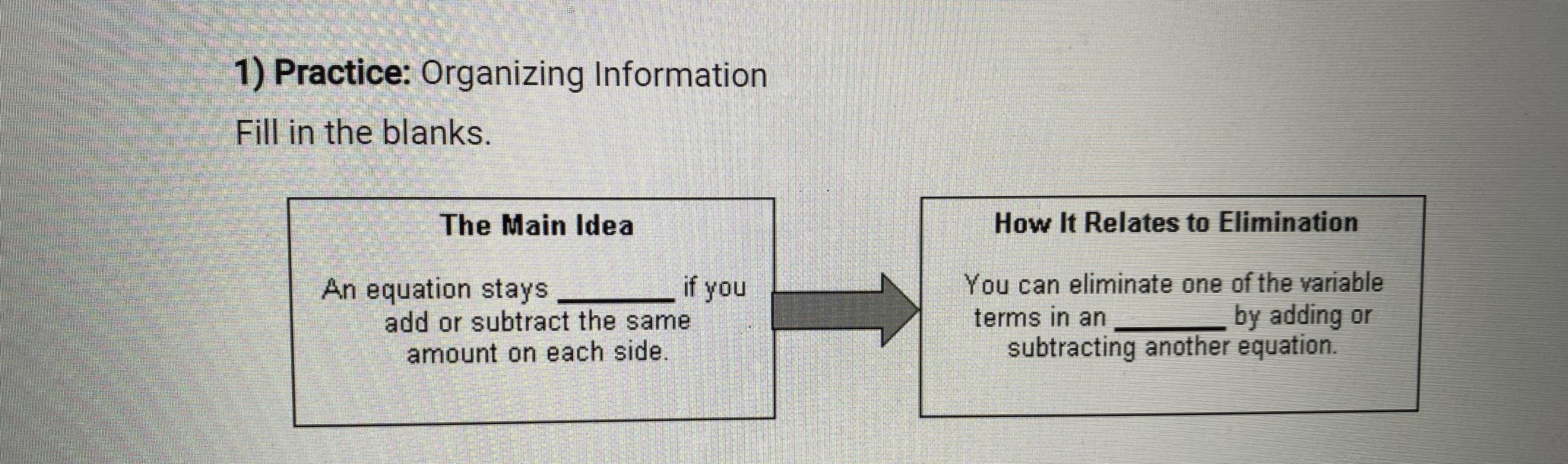
Answers
Answer:
1. remain equal/ stay the same
2. You can eliminate one of the variable terms in a system of equations by adding or subtracting another equation.
Write an expression to model the situation:
Joe is a salesman who makes $200 a week base pay and then $3 for each magazine subscription he sells. Use m for the number of magazines sold.
PLEASE BE ACCURATE!!! THANK YOU!!!:)
Answers
Let's call the total pay for Joe "P". We know that Joe makes a base pay of $200 a week, so we can write the first part of the expression as:
Describe expression using an example.
Term is defined as a constant, a single variable, or a mixture of variables and constants multiplied or divided. Algebra Expression Example: 3x + 9, 5x + 10…
P = 200
In addition to the base pay, Joe makes $3 for each magazine subscription he sells. We can use the variable "m" to represent the number of magazine subscriptions sold, so the second part of the expression can be written as:
P = 200 + 3m
Putting these two expressions together, we get the final expression that models the situation:
P = 200 + 3m
This expression says that Joe's total pay is equal to his base pay of $200 plus $3 for each magazine subscription he sells, where "m" represents the number of magazine subscriptions sold.
Learn more about expression
https://brainly.com/question/1859113
#SPJ1
What is the vertex of f(x)=x^2−12x+25 ?
Answers
Answer:
vertex is (6, -11)
Step-by-step explanation:
Given equation
f(x) = x² - 12x + 25
is that of an upward-facing parabola(since the coefficient of x² is positive).
The vertex will be at a minimum and its x-coordinate can be found by finding the first derivative of f(x), setting it equal to zero and solving for x
f'(x) = d/dx(x² - 12x + 25)
= 2x - 12
f'(x) = 0 ==> 2x - 12 = 0
2x = 12
x = 6
Substitute x = 6 in f(x) to get
f(6) = 6² - 12(6) + 25
= 36 - 72 + 25
= -11
So the vertex is at (6, -11)
NEED HELP ASAP, I WILL GIVE YOU BRAINLIEST
Which one represents the recursive formula for the series -4, -1, 2,...?

Answers
Answer:
sO THE ANSWER TO THIS QUESTION IS 2
Step-by-step explanation:
Which of the points (x, y) does NOT lie on the unit circle a) O P(1,0) b)° 0( 23.-2) c)
Answers
a) The point O P(1,0) lies on the unit circle.
b) The point ° 0(23, -2) does not lie on the unit circle.
c) The information for point c) is missing.
a) The point O P(1,0) lies on the unit circle because its coordinates satisfy the equation x^2 + y^2 = 1. Plugging in the values, we have 1^2 + 0^2 = 1, which confirms that it lies on the unit circle.
b) The point ° 0(23, -2) does not lie on the unit circle because its coordinates do not satisfy the equation x^2 + y^2 = 1. Substituting the values, we get 23^2 + (-2)^2 = 529 + 4 = 533, which is not equal to 1. Therefore, this point does not lie on the unit circle.
c) Unfortunately, the information for point c) is missing. Without the coordinates or any further details, it is impossible to determine whether point c) lies on the unit circle or not.
In summary, point a) O P(1,0) lies on the unit circle, while point b) ° 0(23, -2) does not lie on the unit circle. The information for point c) is insufficient to determine its position on the unit circle.
To learn more about circle click here
brainly.com/question/29142813
#SPJ11
