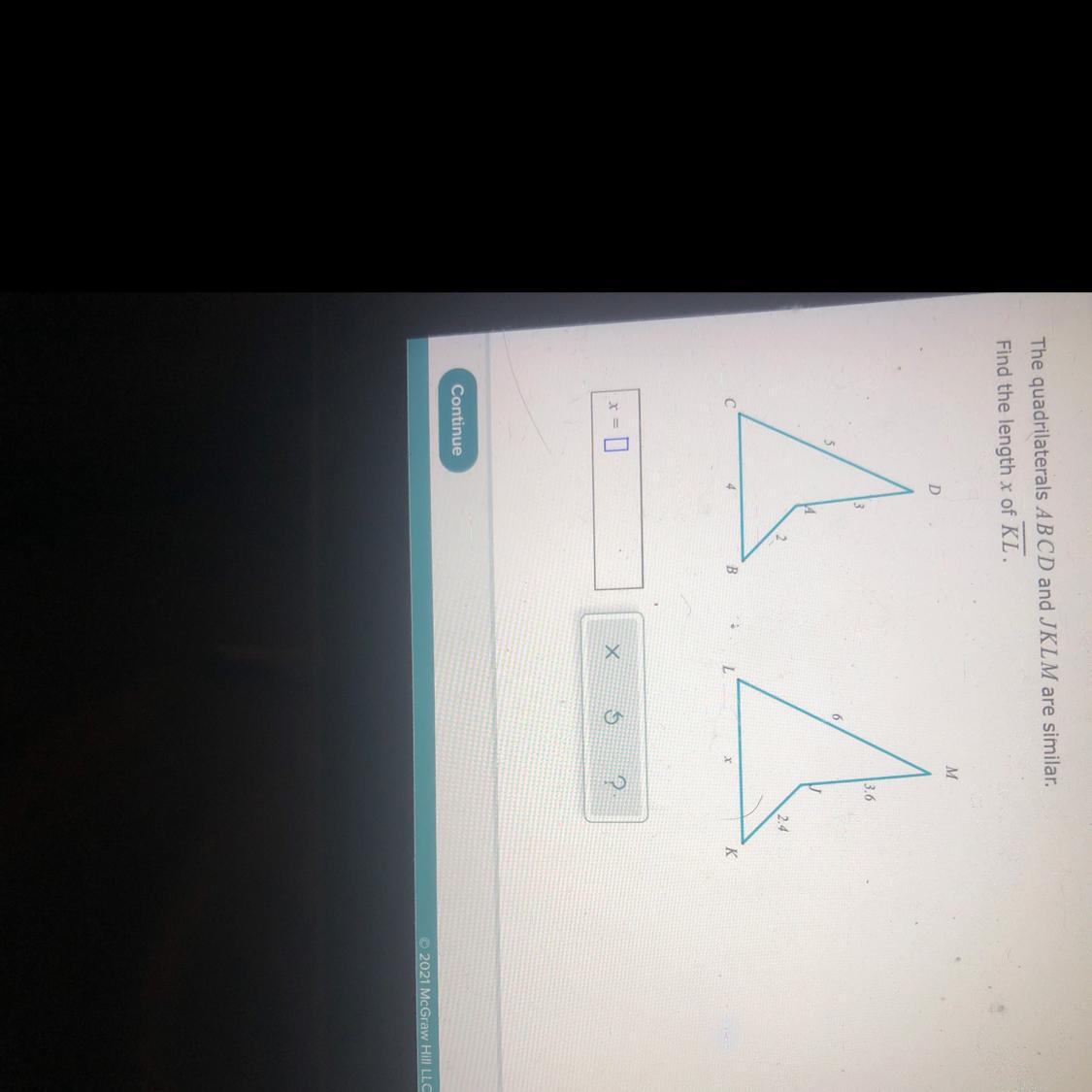
Answers
Answer:
KL = 4.8
Step-by-step explanation:
In similar figures their corresponding parts have the same scale factor.
So CD : LM = 5 : 6
\(\frac{5}{6} = \frac{4}{KL}\)
5KL = 24
KL = 24/5
KL = 4.8
Related Questions
or
1. The starting point of a___ or____
is the endpoint.
Answers
Answer:
1. The starting point of a ray or line segment
is the endpoint.
Step-by-step explanation:
hope it may help you!
Answer:
The starting point of a ray or line segment is the endpoint.
Step-by-step explanation:
hope it may help you
Determined to reduce the Bank's power even before its charter expired, Jackson
removed government deposits from the Bank.
Answers
The given statement refers to an action taken by President Andrew Jackson in the 1830s to diminish the power of the Second Bank of the United States.
In 1833, Jackson ordered the withdrawal of federal government deposits from the Bank and placed them into state-chartered banks. This move was part of Jackson's broader campaign to weaken the Bank's influence over the national economy and to promote the use of state-chartered banks instead.
The Second Bank of the United States had been established in 1816 to regulate the country's money supply and promote economic stability. However, many Americans, including Jackson, believed that the Bank favored the interests of the wealthy over those of ordinary citizens and that it had too much power over the economy.
Jackson's decision to remove government deposits from the Bank was controversial and sparked a political crisis. The Bank's supporters accused Jackson of abusing his presidential power and endangering the stability of the economy. However, Jackson and his allies argued that the Bank was a threat to democracy and that its power needed to be curtailed.
Ultimately, Jackson's actions contributed to the demise of the Second Bank of the United States. When the Bank's charter expired in 1836, it was not renewed, and its functions were gradually taken over by state-chartered banks and other financial institutions.
To know more about the " Second Bank of the United States":https://brainly.com/question/28944191
#SPJ11
What is the difference between qualitative forecasting techniques and quantitative forecasting techniques?
Answers
The difference between qualitative forecasting techniques and quantitative forecasting techniques is:
Quantitative projections frequently rely on historical information, like past sales and income numbers, production and financial reports, and website visitor statistics. You may use seasonal sales data, for instance, to estimate the production and labour requirements for the upcoming year based on the monthly or quarterly results from the previous year. Additionally, statistical modelling, trend analysis, or other information from authoritative sources like governmental organisations, professional groups, and academic institutions are used in quantitative forecasting.
Techniques for qualitative forecasting are derived from the knowledge and intuition of seasoned business professionals. These forecasting methods involve data interpretation together with the expert knowledge you've gained through years of work experience, so they go beyond simple guesswork. For instance, if you require qualitative data to predict sales for the year, you may calculate the influence of a new advertising campaign or promotion your business is preparing, consider the implications of emerging technology for customer behaviour, and consider current social fads and trends.
Learn more about forecasting techniques:
https://brainly.com/question/28494130
#SPJ4
Find the midpoint M of the line segment joining the points S = (0,5) and T = (4,-5).
Answers
Answer:
(0-4)/2 , (5-(-5))/2
-4/2 , (5+5)/2
-2 , 10/2
Midpoint = -2,5
for the matrix samplematrix=[1, 2, 3; 4, 5, 6; 7, 8, 9], to produce samplematrix = [1, 4, 7, 5, 8, 3, 6, 9] with the command samplematrix([n]) = [ ], what should the value of n be?
Answers
To produce `samplematrix = [1, 4, 7, 5, 8, 3, 6, 9]` with the command `samplematrix([n]) = [ ]`, the value of `n` should be 2.
To produce `samplematrix = [1, 4, 7, 5, 8, 3, 6, 9]` with the command `samplematrix([n]) = [ ]`, the value of `n` should be 2. Here's the explanation: Given `samplematrix=[1, 2, 3; 4, 5, 6; 7, 8, 9]`, the command `samplematrix([n]) = [ ]` would remove the nth row from the matrix and leave an empty row in its place.
For example, if `n = 2`, then the command `samplematrix([n]) = [ ]` would remove the second row and leave an empty row in its place.
The resulting matrix would be:`samplematrix = [1, 2, 3; ; 7, 8, 9]`
Notice that there is an empty row in the middle because the second row was removed.
Next, to produce the desired matrix `samplematrix = [1, 4, 7, 5, 8, 3, 6, 9]`, we need to concatenate the rows of the modified `samplematrix` matrix in a specific order. The order is the first row, then the third row, and finally the second row. So, we can use the following code to achieve this:
result = [samplematrix(1,:); samplematrix(3,:); samplematrix(2,:)]
The resulting `result` matrix would be:`result = [1, 2, 3; 7, 8, 9; 4, 5, 6]`
We can then use the colon operator to reshape the matrix into a row vector, like this:`samplematrix = result(:)'`The resulting `samplematrix` vector would be:`samplematrix = [1, 4, 7, 5, 8, 3, 6, 9]`
Therefore, to produce `samplematrix = [1, 4, 7, 5, 8, 3, 6, 9]` with the command `samplematrix([n]) = [ ]`, the value of `n` should be 2.
Learn more about matrix visit:
brainly.com/question/29132693
#SPJ11
What is the length of line segment RS? Use the law of sines to find the answer. Round to the nearest tenth. Triangle Q R S is shown. Angle Q R S is 80 degrees. The length of Q R is 2.4 and the length of Q S is 3.1. Law of sines: StartFraction sine (uppercase A) Over a EndFraction = StartFraction sine (uppercase B) Over b EndFraction = StartFraction sine (uppercase C) Over c EndFraction 2.2 units 2.4 units 3.0 units 3.3 units
Answers
Answer: 2.4 UNITS
Step-by-step explanation:
The sine rule :
Sine A / a = Sine B / b = Sine C / c
From the diagram attached :
QR = s = 2.4 ; QS =r = 3.1 ; RS =q =?
We need to find the angle RQS
using Sine rule :
Sine R / r = Sine S / s
Sin 80° / 3.1 = sin S / 2.4
0.9848077 / 3.1 = sin S / 2.4
Sin S × 3.1 = 0.9848077 × 2.4
Sin S = 2.3635386 / 3.1
Sin S = 0.7624318
S = Sin^-1(0.7624318)
S = 49.67°
Therefore, form using ;
A + B + C = 180° ( SUM of angles in a triangle)
SQR = 180° - (QRS + QSR)
= 180° - ( 80 + 49.67)° = 50.33°
Q = 50.33°
THEREFORE,
Sine Q / q = Sin S / s
Sin 50.33° / q = Sin 49.67° / 2.4
0.7697339 / q = 0.7623295 / 2.4
0.7623295q = 0.7697339 × 2.4
q = 1.84736136 / 0.7623295
q = 2.4233108
q = Segment RS = 2.4units

Answer:
B) 2.5 is the right answer
Step-by-step explanation:
i got 100%
solve the differential equation by variation of parameters. y'' + y = cos2(x)
Answers
Answer:
\(y=c_1\cos(x)+c_2\+\sin(x)+\sin^2(x)-\frac{1}{3}\sin^4(x)+\frac{1}{3}\cos^4(x)}}}\)
Step-by-step explanation:
Given the second-order differential equation, \(y'' + y = cos2(x)\), solve it using variation of parameters.
(1) - Solve the DE as if it were homogenous and find the homogeneous solution\(y'' + y = cos2(x) \Longrightarrow y'' + y =0\\\\\text{The characteristic equation} \Rightarrow m^2+1=0\\\\m^2+1=0\\\\ \Longrightarrow m^2=-1\\\\\ \Longrightarrow m=\sqrt{-1} \\\\\Longrightarrow \boxed{m=\pm i} \\ \\\text{Solution is complex will be in the form} \ \boxed{y=c_1e^{\alpha t}\cos(\beta t)+c_2e^{\alpha t}\sin(\beta t)} \ \text{where} \ m=\alpha \pm \beta i\)
\(\therefore \text{homogeneous solution} \rightarrow \boxed{y_h=c_1\cos(x)+c_2\sin(x)}\)
(2) - Find the Wronskian determinant
\(|W|=\left|\begin{array}{ccc}y_1&y_2\\y'_1&y'_2\end{array}\right| \\\\\Longrightarrow |W|=\left|\begin{array}{ccc}\cos(x)&\sin(x)\\-sin(t)&cos(x)\end{array}\right|\\\\\Longrightarrow \cos^2(x)+\sin^2(x)\\\\\Longrightarrow \boxed{|W|=1}\)
(3) - Find W_1 and W_2
\(\boxed{W_1=\left|\begin{array}{ccc}0&y_2\\g(x)&y'_2\end{array}\right| and \ W_2=\left|\begin{array}{ccc}y_2&0\\y'_2&g(x)\end{array}\right|}\)
\(W_1=\left|\begin{array}{ccc}0&\sin(x)\\\cos^2(x)&\cos(x)\end{array}\right|\\\\\Longrightarrow \boxed{W_1= -\sin(x)\cos^2(x)}\\\\W_2=\left|\begin{array}{ccc}\cos(x)&0\\ -\sin(x)&\cos^2(x)\end{array}\right|\\\\\Longrightarrow \boxed{W_2= \cos^3(x)}\)
(4) - Find u_1 and u_2
\(\boxed{u_1=\int\frac{W_1}{|W|} \ and \ u_2=\int\frac{W_2}{|W|} }\)\
u_1:
\(\int(\frac{-\sin(x)\cos^2(x)}{1}) dx\\\\\Longrightarrow-\int(\sin(x)\cos^2(x)) dx\\\\\text{Let} \ u=\cos(x) \rightarrow du=-sin(x)dx\\\\\Longrightarrow\int u^2 du\\\\\Longrightarrow \frac{1}{3}u^3\\ \\\Longrightarrow \boxed{u_1=\frac{1}{3}\cos^3(x)}\)
u_2:
\(\int\frac{\cos^3(x)}{1}dx\\ \\\Longrightarrow \int \cos^3(x)dx\\\\ \Longrightarrow \int (\cos^2(x)\cos(x))dx \ \ \boxed{\text{Trig identity:} \cos^2(x)=1-\sin^2(x)}\\\\\Longrightarrow \int[(1-\sin^2(x)})\cos(x)]dx\\\\\Longrightarrow \int \cos(x)dx-\int (\sin^2(x)\cos(x))dx\\\\\Longrightarrow \sin(x)-\int (\sin^2(x)\cos(x))dx\\\\\text{Let} \ u=\sin(x) \rightarrow du=cos(x)dx\\\\\Longrightarrow \sin(x)-\int u^2du\\\\\Longrightarrow \sin(x)-\frac{1}{3} u^3\)\
\(\Longrightarrow \boxed{u_2=\sin(x)-\frac{1}{3} \sin^3(x)}\)
(5) - Generate the particular solution
\(\text{Particular solution} \rightarrow y_p=u_1y_1+u_2y_2\)
\(\Longrightarrow y_p=(\frac{1}{3}\cos(x))(\cos(x))+(\sin(x)-\frac{1}{3} \sin^3(x))(\sin(x))\\\\ \Longrightarrow y_p=\frac{1}{3}\cos^4(x)+\sin^2(x)-\frac{1}{3}\sin^4(x)\\\\\Longrightarrow \boxed{y_p=\sin^2(x)-\frac{1}{3}\sin^4(x)+\frac{1}{3}\cos^4(x)}\)
(6) - Form the general solution
\(\text{General solution} \rightarrow y_{gen.}=y_h+y_p\)
\(\boxed{\boxed{y=c_1\cos(x)+c_2\+\sin(x)+\sin^2(x)-\frac{1}{3}\sin^4(x)+\frac{1}{3}\cos^4(x)}}}\)
Thus, the solution to the given DE is found where c_1 and c_2 are arbitrary constants that can be solved for given an initial condition. You can simplify the solution more if need be.
Given the first four terms of a linear pattern: 3; x; y; 30
Calculate the values of x and y
Answers
It should be noted that based on the information given, the values of x and y in the linear pattern will be 12 and 21.
How to illustrate the information?It should be noted that since this is a linear pattern, it should be noted that it illustrates that the values in between them are the same.
It should be noted that the numbers that fits into the scenario are 3, 12, 21 and 30. There's a difference of 9 between them.
Therefore, it should be noted that based on the information given, the values of x and y in the linear pattern will be 12 and 21.
Learn more about numbers on:
brainly.com/question/24644930
#SPJ1
There are 4 pink, 5 yellow, 2 violet, and 3 gray marbles in a hat. You pick 2 marbles from the hat. Marbles are NOT returned to the hat.

Answers
A. The probability of selecting a pink marble first and then a violet marble is 4/91.
B. The probability of selecting a gray marble first and then another gray marble is 3/91.
C. The probability of selecting a non-yellow marble first and then another non-yellow marble is 9/26.
D. The probability of selecting a yellow marble first and then a non-yellow marble is 20/91.
To solve these probabilities, we need to consider the number of marbles of each color and the total number of marbles remaining in the hat after each selection.
Let's calculate the probabilities step by step:
A. P(PINK, THEN VIOLET):
The probability of selecting a pink marble first is 4/14 (4 pink marbles out of 14 total marbles).
After the first marble is selected, there are 13 marbles remaining in the hat, with 2 violet marbles.
The probability of selecting a violet marble second is 2/13 (2 violet marbles out of the remaining 13 marbles).
To find the probability of both events occurring, we multiply the individual probabilities:
P(PINK, THEN VIOLET) = (4/14) * (2/13) = 8/182 = 4/91
B. P(GRAY, THEN GRAY):
The probability of selecting a gray marble first is 3/14 (3 gray marbles out of 14 total marbles).
After the first marble is selected, there are 13 marbles remaining in the hat, with 2 gray marbles.
The probability of selecting a gray marble second is 2/13 (2 gray marbles out of the remaining 13 marbles).
To find the probability of both events occurring, we multiply the individual probabilities:
P(GRAY, THEN GRAY) = (3/14) * (2/13) = 6/182 = 3/91
Therefore, the probability of selecting a gray marble first and then another gray marble is 3/91.
C. P(NOT YELLOW, NOT YELLOW):
The probability of selecting a non-yellow marble first is (14 - 5)/14 = 9/14 (9 non-yellow marbles out of 14 total marbles).
After the first marble is selected, there are 13 marbles remaining in the hat, with (5 - 1) yellow marbles (since one yellow marble was already picked).
The probability of selecting a non-yellow marble second is (13 - 4)/13 = 9/13 (9 non-yellow marbles out of the remaining 13 marbles).
To find the probability of both events occurring, we multiply the individual probabilities:
P(NOT YELLOW, NOT YELLOW) = (9/14) * (9/13) = 81/182 = 9/26
Therefore, the probability of selecting a non-yellow marble first and then another non-yellow marble is 9/26.
D. P(YELLOW, NOT YELLOW):
The probability of selecting a yellow marble first is 5/14 (5 yellow marbles out of 14 total marbles).
After the first marble is selected, there are 13 marbles remaining in the hat, with (14 - 5) - 1 = 8 non-yellow marbles (since one yellow marble was already picked).
The probability of selecting a non-yellow marble second is 8/13 (8 non-yellow marbles out of the remaining 13 marbles).
To find the probability of both events occurring, we multiply the individual probabilities:
P(YELLOW, NOT YELLOW) = (5/14) * (8/13) = 40/182 = 20/91
For more question on probability click on
https://brainly.com/question/251701
#SPJ11
Can you please help me with this problem!!

Answers
Answer:
.
Step-by-step explanation:
1/7 * 3/5
1/3 * 1 1/7 * 1/4
Answers
Answer:
3/35
11/84
Step-by-step explanation:
1/7*3/5=3/35
1*3=3
7*5=35
1/3*11/7*1/4=11/84
1*11*1=11
3*7*4=84
example of an augmented matrix that has a free variable, but does not have infinitely many solutions.
Answers
The system of equations represented by this matrix has only one unique solution (x=2, y=-3). Thus, even though there is a free variable, there are no other solutions for the system.
An augmented matrix is a representation of a system of linear equations. To have a free variable means that there is at least one column in the augmented matrix that does not have a leading 1. However, having a free variable does not necessarily mean that the system has infinitely many solutions.
An example of an augmented matrix with a free variable but not infinitely many solutions is:
[ 1 0 2 | 4 ]
[ 0 1 -3 | 6 ]
[ 0 0 0 | 0 ]
In this matrix, the first and second columns have leading 1's, indicating that they are pivot columns. The third column, however, does not have a leading 1 and therefore represents a free variable.
Despite this, the system of equations represented by this matrix has only one unique solution (x=2, y=-3). Thus, even though there is a free variable, there are no other solutions for the system.
This example satisfies the criteria of having a free variable but not infinitely many solutions.
To know more about linear equations visit:
https://brainly.com/question/29111179
#SPJ11
An augmented matrix can have a free variable but still have a unique solution if it is not over-determined or inconsistent.
An example of an augmented matrix that has a free variable but does not have infinitely many solutions can be represented by the following:
\(\left[\begin{array}{cccc}1&0&|&2\\0&1&|&3\\0&0&|&0\end{array}\right]\)
In this augmented matrix, the last row consists of all zeros, indicating a linearly dependent equation. The presence of a free variable can be observed in the fact that the matrix does not have a unique solution.
To understand why this matrix does not have infinitely many solutions, we can interpret it as a system of linear equations. The first row represents the equation x = 2, while the second row represents y = 3. The last row, with all zeros, implies 0 = 0, which is always true.
Since the system has a free variable, it means there are infinitely many possible values for the variables x and y that satisfy the system. However, despite the presence of a free variable, the system does not have infinitely many solutions. Instead, it has a unique solution (x = 2, y = 3). This is because the last row of zeros indicates that the system is not over-determined or inconsistent.
In conclusion, an augmented matrix can have a free variable but still have a unique solution if it is not over-determined or inconsistent.
Learn more about augmented matrix from the given link:
https://brainly.com/question/30403694
#SPJ11
The calculation of SNN distance does not take into account the position of shared neighbors in the two nearest neighbor lists. In other words, it might be desirable to give higher similarity to two points that share the same nearest neighbors ranked higher in the nearest neighbor lists. Describe how you might modify the definition of SNN similarity to achieve that. Justify your modification.
Answers
By incorporating this information into the similarity measure, we can produce more accurate and informative results in clustering and classification tasks.
To modify the definition of clustering similarity to take into account the position of shared neighbors in the two nearest neighbor lists, we can introduce a weighting factor that considers the rank of the shared neighbor in each list. This can be achieved by multiplying the regular SNN similarity value by a weight factor that is calculated as the reciprocal of the sum of the ranks of the shared neighbors in the two lists. For example, if two points have a shared neighbor that is ranked 2nd in one list and 3rd in the other list, the weight factor would be 1/(2+3) = 0.2. This weight factor would then be multiplied by the regular SNN similarity value to produce a modified SNN similarity score that gives higher similarity to points that share the same nearest neighbors ranked higher in the nearest neighbor lists. This modification is justified because it takes into account the fact that having shared neighbors that are ranked higher in the nearest neighbor lists is a stronger indicator of similarity than having shared neighbors that are ranked lower.
Learn more about clustering here
https://brainly.com/question/29888905
#SPJ11
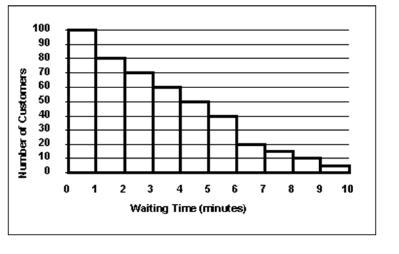
The staff of Mr. Wayne Wertz, VP of Operations at Portland Peoples Bank, prepared a frequency histogram of waiting time for walk-in customers. Approximately how many walk-in customers waited at least 6 minutes? (Note the position of the labels on the x-axis — the first column is the number of customers who waited 1 minute and the last column is the number of customers who waited 10 minutes)
Answers
The number of people who waited at least 6 minutes is given as follows:
50 people.
What is shown by the histogram?The height of each bin of the histogram represents the number of observations of the data-set in the desired interval.
The desired outcomes for this problem are given as follows:
Between 6 and 7 minutes: 20 people.Between 7 and 8 minutes: 15 people.Between 8 and 9 minutes: 10 people.Between 9 and 10 minutes: 5 people.Hence the number of people who waited at least 6 minutes is given as follows:
20 + 15 + 10 + 5 = 50 people.
More can be learned about histograms at brainly.com/question/25983327
#SPJ1
Verify that P = (1, −1) is the same distance from A = (5, 1) as it is from B = (−1, 3).
It is customary to say that P is equidistant from A and B. Find two more points that are equidistant from A and B. Can points equidistant from A and B be found in every quadrant? Explain.
Answers
The given statement is true that the distance of P to A is equal to the distance from P to B.
Given that,
To verify that P = (1, −1) is the same distance from A = (5, 1) as it is from B = (−1, 3).
Coordinate, is represented as the values on x axis and y-axis of the graph
Here,
According to the question,
AP = PB
√[(5-1)² + (1+1)²] = √[(1+1)² + (3 + 1)²]
√[16 + 4] = √[16 + 4]
√20 = √20
it implies the distance of point P from Point A is equal to the distance of P from B.
Thus, the given statement is true that the distance of P to A is equal to the distance from P to B.
Learn more about coordinate here:
brainly.com/question/13498438
#SPJ1
(#9) 12am=4 solve for a
pls help me
Answers
Answer:
a=1/3m
Step-by-step explanation:
Divide each side by 12m and then you simplify it
A. What is the slope of 2x-4y=4?
Answers

X=2y + 2 & here is a picture :)

A triangle has side lengths of (7x-4)(7x−4) centimeters, (x+3)(x+3) centimeters, and (3y+2)(3y+2) centimeters. Which expression represents the perimeter, in centimeters, of the triangle?
Answers
The perimeter of the triangle is, 8x + 3y +1.
What is perimeter?
A perimeter is a closed path that encloses, surrounds, or delimits a one-dimensional length, a two-dimensional shape, or both. The circumference of a circle or an ellipse is its perimeter. There are numerous practical uses for calculating the perimeter.
Let, the side lengths of the triangle are (7x - 4), (x + 3) and (3y + 2).
Since the perimeter is the sum of all side lengths.
So,
Perimeter = (7x - 4) + (x + 3) + (3y + 2)
= 7x - 4 + x + 3 + 3y + 2
Perimeter = 8x + 3y + 1
Hence, the perimeter of the triangle is, 8x + 3y + 1.
To know more about the perimeter, click on the link
https://brainly.com/question/25092270
#SPJ1
int \( a[4]=\{1,2,3,4\} \) int \( { }^{*} p=a \); What is the value of \( *(p+3) ? \)
Answers
The value of the expression is 4.
The code :
int a[4] = {1, 2, 3, 4};
int *p = a;
what is *(p + 3)?
The variable a is an array of integers, and the variable p is a pointer to the first element of the array.
The expression *(p + 3) is the value of the element of the array that is 3 elements after the element that p points to.
Since p points to the first element of the array, the expression *(p + 3) is the value of the fourth element of the array, which is 4.
Therefore, the value of the expression is 4.
Here is a breakdown of the code:
int a[4] = {1, 2, 3, 4}: This line declares an array of integers called a and initializes it with the values 1, 2, 3, and 4.
int *p = a; This line declares a pointer to an integer called p and initializes it with the address of the first element of the array a.
what is *(p + 3)?: This line asks what the value of the expression *(p + 3) is.
The expression *(p + 3) is the value of the element of the array that is 3 elements after the element that p points to.
Since p points to the first element of the array, the expression *(p + 3) is the value of the fourth element of the array, which is 4.
Therefore, the value of the expression is 4.
To learn more about expression here:
https://brainly.com/question/28170201
#SPJ4
Correct Question :
Int a[4]={1,2,3,4}, int *p=a. What is the value of *(p+3)?
The equation y = 5x represents a proportional relationship. what is the constant of proportionality
A. 1/5
B. x
C. 0
D. 5
Answers
Answer:
the constant of proportionality is 5-D
Help asap, The graph compares the total cost of buying movie tickets for members and nonmembers of a movie club
Answers
A negative correlation is the relationship where an increase in one of the variable say x lead to a decrease in the other variable say y
In the question given, the variables are the number of workers in the x- axis and the hours of complete job in the y axis
Therefore option C is the only option where increase in the number of workers led to decrease in the hours of complete job
Hence the correct answer is option C
Use an appropriate area formula to find the area of the triangle with the given side lengths. a = 15 m b=9 m c=14 m The
Answers
The area of the triangle with side lengths 15 m, 9 m, and 14 m is approximately 61.639 square meters.
To find the area of a triangle given the lengths of its sides, we can use Heron's formula. Heron's formula states that the area (A) of a triangle with side lengths a, b, and c can be calculated using the semi-perimeter (s) of the triangle.
The semi-perimeter (s) is calculated as the sum of the lengths of the sides divided by 2:
s = (a + b + c) / 2
Once we have the semi-perimeter, we can calculate the area using the formula:
A = √(s(s - a)(s - b)(s - c))
Substituting the given side lengths into the formula:
a = 15 m
b = 9 m
c = 14 m
s = (15 + 9 + 14) / 2 = 19
A = √(19(19 - 15)(19 - 9)(19 - 14))
A = √(19(4)(10)(5))
A = √(3800) ≈ 61.639 m²
Know more about triangle here:
https://brainly.com/question/2773823
#SPJ11
The volume of the rectangular prism below is 192 cubic centimeters.
Which equation can be used to find the height of the prism?
A.h=6⋅4
B.h=192÷
(6⋅4
)
C.h=192⋅6⋅4
D.h=192−
(6⋅4
)
Answers
Answer: B. h=192÷ (6⋅4)
Step-by-step explanation:
B. h=192÷ (6⋅4)
This equation can be used to find the height of the prism because the volume of a rectangular prism can be represented by the equation V = l*w*h, where l and w are the length and width, respectively, and h is the height. In this case, given that V=192, the equation h=192÷ (l*w) can be used to find the height, where l=6 and w=4.
Y=3x-2 solve for x plz help 40 points!!!
Answers
Answer:
x=\(\frac{y+2}{3}\)
Step-by-step explanation:
1) since we are solving for x we want x to be the ONLY thing on the other side of the equation symbol:
for ex. x=
2) to do this, we need to eliminate -2, we eliminate -2 by adding 2 on both sides:
y+2=3x-2+2
y+2=3x
remove 3 by dividing it on both sides(opposite operation)
\(\frac{y+2}{3}\)=x
this is our final equation since we have solved for x
hope this helps
find the probability of choosing a letter other than the letter a from a bag that contains the fifteen letters of the indian city palasa kasibugga. express your answer as a fraction in lowest terms or a decimal rounded to the nearest millionth.
Answers
The probability of choosing a letter other than the letter a from a bag that contains the fifteen letters of the Indian city Palasa Kasibugga is 11/15.
According to the question,
We have the following information:
Words are:
Palasa Kasibugga
Now, total number of letters = 15
Number of a in these words = 4
Number of letters other than a = 11
We know that the following formula is used to find the probability of an event:
Probability = Number of favorable outcomes/total number of outcomes
Probability = 11/15
Hence, the probability of choosing a letter other than the letter a from a bag that contains the fifteen letters of the Indian city Palasa Kasibugga is 11/15.
To know more about probability here
https://brainly.com/question/11234923
#SPJ4
Which proportion could be used to find the missing side length?
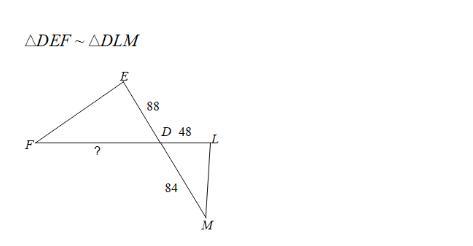
Answers
Answer:
Step-by-step explanation:
ED : DL = FD : DM
or
ED / DL = FD / DM
FD = ED·DM / DL
FD = 88 · 84 / 48 = 154
Kiaya has to have at least $100 in her checking account to avoid a fee from the bank. She has $376 in her account now. Each week, she makes a $25 withdrawal. For how many weeks can she make this withdrawal and avoid a fee?
Answers
Answer:
11 weeks
Step-by-step explanation:
Kiaya has $376 but can only withdraw $276 before being charged by the bank.
First I subtracted the $100 she can't spend from $376.
-She has a total of $276 she can spend without being charged.
Next, I divided $276 by $25 (the amount she withdraws every week)
- The total is 11.04
This means she has 11 Weeks before she will have to pay the fee.
Hope I helped you out!! :)
Alan and Jorge are selling popcorn to earn money for a school trip.
Alan's popcorn sales can be represented by the equation y=2x, where x is the number of bags of popcorn sold and y is the amount of money raised.
Jorge's popcorn sales can be represented by this graph.If both boys sell the same amount of popcorn, who will raise the most money? Why?
Select the answer that is entirely correct.
Responses
Jorge will raise more money because he is selling the popcorn for $3 per bag, and Alan is selling the popcorn for $2 per bag.
Jorge will raise more money because he is selling the popcorn for 3 dollars per bag, and Alan is selling the popcorn for 2 dollars per bag.
Alan will raise more money because he is selling the popcorn for $3 per bag, and Jorge is selling the popcorn for $2 per bag.
Alan will raise more money because he is selling the popcorn for 3 dollars per bag, and Jorge is selling the popcorn for 2 dollars per bag.
Jorge will raise more money because he is selling the popcorn at 2 bags for a $1, and Alan is selling the popcorn at 3 bags for $1.Jorge will raise more money because he is selling the popcorn at 2 bags for a 1 dollars and Alan is selling the popcorn at 3 bags for
Alan will raise more money because he is selling the popcorn at 2 bags for a $1, and Jorge is selling the popcorn at 3 bags for $1.Alan will raise more money because he is selling the popcorn at 2 bags for a 1 dollars and Jorge is selling the popcorn at 3 bags for

Answers
The answer that is entirely correct based on the sales of popcorn is;
A: Jorge will raise more money because he is selling the popcorn for $3 per bag, and Alan is selling the popcorn for $2 per bag.
How to interpret Linear Equations?
The general form of the equation of a line in slope intercept form is;
y = mx + c
where;
m is slope
c is y-intercept
Now, For Alan, we are told that her popcorn sales can be represented by the equation; y = 2x
where;
x is the number of bags of popcorn sold.
y is the amount of money raised.
Thus, if x is the number of bags of popcorn sold, then it means that the cost of each bag is $2
Now, for Jorge, looking at the graph, we can see that;
y -intercept = 0
Slope = (15 - 6)/(5 - 2)
Slope = 3
Thus, if x is the number of bags of popcorn sold, then it means that the cost of each bag is $3.
Looking at the options, the correct one are Options A,
Read more about linear equations at; https://brainly.com/question/14323743
#SPJ1
Sharon and Tim each opene a savings account on the same day. Sharon started by putting $15 in her account, and she will deposit an additional $7 each week. Tim made an initial deposit of $35, and he will add $3 more each week. Eventually, Sharon and Tim will each have the same amount saved. What is that amount?
Answers
$15 + $35 (5 weeks) = $50
$35 + $15 (5 weeks) = $50
Answer:
Step-by-step explanation:
Sharon y = 7x + 15
Tim y = 3x + 35
7x + 15 = 3x + 35
4x + 15 = 35
4x = 20
x = 5 weeks
Sharon: 7(5) + 15 = 35 + 15 = $50
Tim: 3(5) + 35 = 15 + 35 = $50
MARIA IS GOING FOR A RUN. AFTER 20 MINUTES, SHE HAS
RUN 3 MILES. AFTER 2 HOURS, SHE HAS RUN 14.5 MILES.
WHAT IS MARIA'S SPEED?

Answers
Answer:
7.25 mph(miles per hour)
Step-by-step explanation: