Answers
Answer:
5^15
and x^10
explanation:
when the base is the same you add the exponents (the numbers on top) so look above to see that they are just adding
Related Questions
25 points !!! ( pls don’t answer if you don’t have the answer I will report you)
Look at the picture A cube has a volume of 27 cubic units. A square has an area of 16 square units. Which of the following statements is true?

Answers
side length of square =4
side length of cube=3
hence the correct statement is,
the side length of the cube is less than the side length of the square
If the point (2,5) is a solution to the system of equations shown below, then determine the missing values of b and m. Show how you arrive at your answer. y=3x+b y=mx+9
Answers
The missing value of b is -1 and the missing value of m is -2.To determine the missing values of b and m in the system of equations,
we can substitute the given point (2,5) into each equation and solve for the variables.
First, substitute the point (2,5) into the equation y = 3x + b:
5 = 3(2) + b
Simplify the equation:
5 = 6 + b
Subtract 6 from both sides:
5 - 6 = b
-1 = b
Therefore, the missing value of b is -1.
Next, substitute the point (2,5) into the equation y = mx + 9:
5 = 2m + 9
Simplify the equation:
5 - 9 = 2m
-4 = 2m
Divide both sides by 2:
-4/2 = m
-2 = m
Therefore, the missing value of m is -2.
To summarize:
b = -1
m = -2
By substituting the point (2,5) into each equation, we determined that the missing value of b is -1 and the missing value of m is -2.
learn more about equation here: brainly.com/question/29657983
#SPJ11
solve the initial value problem with y' = (x y-4)^2 with y(0) = 0
Answers
The solution to the initial value problem is y = -(4/3)x3 + (4/2)x2 + c
To solve this initial value problem, use the following steps:
Separate the variables:
y' = (x y - 4)2
Integrate with respect to x:
y' dx = (x y - 4)2 dx
Solve the integral:
y' dx = (x3 y/3 - 4x2/2) + C
Substitute the initial value y(0) = 0 and solve for C:
0 = (x3 y/3 - 4x2/2) + C
C = -4/2
Putting the constant back into the equation and solve for y:
=>y' dx = (x3 y/3 - 4x2/2 - 4/2 )
=>y = -(4/3)x3 + (4/2)x2 + c Where c is an arbitrary constant.
To know more initial value problem, refer here:
https://brainly.com/question/30547172#
#SPJ11
A meteorologist is measuring the temperature every 15 minutes. She notices the temperature increases by 3/4 degrees Fahrenheit between each measurements for 2 hours. What is the rate per hour of the temperature increase?
Answers
Answer:
3 °F/h
Step-by-step explanation:
The rate per hour of temperature change = change in temperature per measurement/change in time per measurement.
Now, the change in temperature per measurement is constant = 3/4 °F and the change in time per measurement is constant = 15 minutes = 15/60 h = 1/4 h.
So, rate per hour of temperature change = change in temperature per measurement/change in time per measurement
= 3/4 °F ÷ 1/4 h
= 3/4 °F × 4/h
= 3 °F/h
So, the rate per hour of temperature change is 3 °F/h
sing a TI-84 calculator, find the area under the standard normal curve to the left of the following z-values. Round the answers to four decimal places. Part 1 of 4 The area to the left of z= 1.07
Answers
The area to the left of z=1.07 is approximately 0.8577 (rounded to four decimal place. To find the area under the standard normal curve to the left of z = 1.07 using a TI-84 calculator.
Follow these steps:
1. Press the "2nd" button, then press "Vars" to access the "DISTR" menu.
2. Scroll down to "normalcdf(" and press "Enter".
3. Enter -99999 (or -E99) as the lower limit, since we want to find the area to the left of z = 1.07, which is very close to negative infinity.
4. Enter 1.07 as the upper limit, since we want to find the area to the left of this value.
5. Enter 0 as the mean, since we're working with the standard normal distribution.
6. Enter 1 as the standard deviation, since we're working with the standard normal distribution.
7. Press "Enter" to calculate the area.
The answer should be approximately 0.8577 when rounded to four decimal places.
Learn more about area here:
https://brainly.com/question/27683633
#SPJ11
vertex represents a maximum or minimum point for the function. Explain your
answer.
b. Rewrite f(x) in vertex form by completing the square.
2. A cannonball is shot from the top of an ocean cliff as shown. The height (in meters) of the cannonball above th
water is given by h(t) = -5t2 + 15t + 8, where t is the number of seconds after the shot. Determine
whether each statement is true according to the graph. Select True or False for each statement.
Statement
True
Fal
The cannon is 8 meters above the water.
The cannonball reaches its maximum height at 1.5
seconds after it is shot.
The cannonball hits the water 8 seconds after it is
shot.
Answers
Answer:
the vertex represents a maximum
Vertex is (4,7)
f(x)=-(x-4)^2+7
Step-by-step explanation:
Given the function \(f(x)=-x^2+8x+9\)
Equation is in the form of y=ax^2+bx+c
\(a=-1\)
When 'a' is negative, then vertex is maximum
when 'a' is positive, then vertex is minimum
\(a=-1\) is negative, so the vertex represents a maximum
\(f(x)=-x^2+8x+9\), factor out negative
Take out negative sign in common
NEED HELP ASAP 3.) Steve was looking to download some movies to his Netflix account to watch on his plane trip so he did not have to pay for wifi on the trip. He started downloading the first movie in the evening but paused the download with 2.3 GB's left to download in the morning. He started the second movie, a 3.9 GB file, in the morning at the same time as the first movie. The first movie took 37 minutes to download the remaining 2.3 GB's while the second took 74 minutes to download the entire 3.9 GB file. Which movie downloaded faster? Show how you found your result.
Answers
The speed of download of the first movie is 0.0621621621621622 GB/min and the speed of download of the second movie is 0.0527027027027027 GB/min. The second movie downloaded faster.
What is speed?
The speed of an object, which is a scalar quantity in everyday usage and kinematics, is the size of the change in that object's position over time or the size of the change in that object's position per unit of time.
It took time to download 2.3 GB's of the first movie is 37 minutes.
It took time to download 3.9 GB's of the first movie is 74 minutes.
Thus the speed of download of the first movie is
GB/ time
= 2.3/37
= 0.0621621621621622 GB/min
Thus the speed of download of the second movie is
GB/ time
= 3.9/74
= 0.0527027027027027 GB/min
The speed of download of the second movie is more than the speed of download of the first movie.
To learn more about download of movie, click on the below link:
https://brainly.com/question/25264064
#SPJ1
Which of the following is the rule for the geometric sequence 1, 3, 9, 27, . . .?
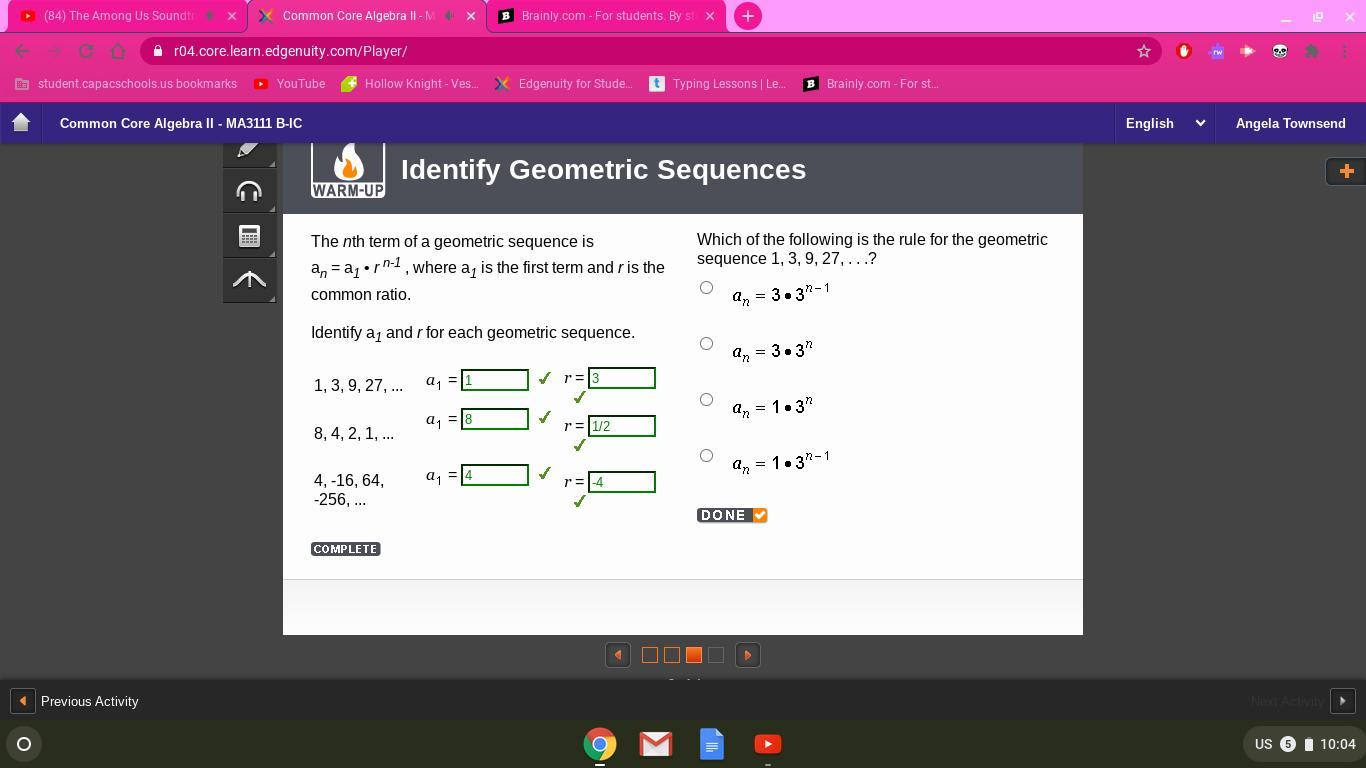
Answers
Answer:
\(a(n) = 1 \times {3}^{n - 1} \)
Step-by-step explanation:
We started at 1And it seems that index after index it multiplies by 3The formula for the geometric sequence defined implicitly is a(n) =a(1)r^(n-1)\(a(n) = a(1) {r}^{n - 1} \\ a(n) = 1 \times {3}^{n - 1} \)
Answer:
D
Step-by-step explanation:
Which of the following statement/s is/are correct? I. A statistic can never be larger than a parameter II. A statistic can never be equal to zero III. A statistic can never be smaller than a parameter IV. A statistic can be calculated whereas a parameter can never be established V. A statistic can never be equal to a parameter A. I, II, III and IV B. V Only c. None of these D. IV and V E. IV Only
Answers
A statistic can never be larger than a parameter is not a correct statement. The correct statement among the following is as follows: IV Only. The statement "A statistic can be calculated whereas a parameter can never be established" is the correct statement.
Statistics and parameters are two fundamental concepts in statistical analysis. Both of these concepts are widely used in various researches and surveys.
A statistic is a numerical value that represents a particular characteristic of the sample and is used to estimate an unknown parameter. A parameter is a numerical value that represents a particular characteristic of a population.Statistics can be larger, smaller, or equal to parameters. A statistic is a value that is calculated from a sample, whereas a parameter is a value that represents a population characteristic and is estimated from the sample.A parameter can be established, but it is only possible if the entire population is considered for analysis. In contrast, a statistic is calculated from a sample of the population and represents only the characteristics of the sample.
:A statistic can never be larger than a parameter is not a correct statement. The correct statement is IV Only. The statement "A statistic can be calculated whereas a parameter can never be established" is the correct statement.
To know more about statistic visit:
brainly.com/question/31538429
#SPJ11
The radius of a circle is 10 cm. Find its area in terms of π.
Answers
The area of a circle is given by the formula:
A = πr^2
where r is the radius of the circle.
Substituting the value of the radius as r = 10 cm, we get:
A = π(10)^2
A = 100π
Therefore, the area of the circle with radius 10 cm is 100π square centimeters.
~~~Harsha~~~
5(x-2)=x+1
Pls help
(No spam)
Pls show work
Answers
Answer:
\(5(x - 2) = x + 1 \\ 5x - 10 = x + 1 \\ 5x - x = 1 0+ 1 \\ 4x = 11 \\ x = \frac{11}{4} \)
Which of the following points is a solution to the system of equations shown?
y - x = -1
x + y = -5
Answers
`●.`●.`●.`●.`●.`●.`●.`●.`●.`●.`●.`●.`●.`●.`●.`●.`●.`●.
\(\quad \qquad \huge \bf \dag \: Answer \: \dag\)
`●.`●.`●.`●.`●.`●.`●.`●.`●.`●.`●.`●.`●.`●.`●.`●.`●.`●.
\( \underline{ \large \rm Solution} : \)
\(\rm Given : \)
Two equations are -
y - x = -1 (i)x + y = -5 (ii)\( \rm Procedure : \)
Considering the equations as (i) and (ii) respectively
From equation (i) -
y = x - 1put this value of y in equation (ii) -
x + y = -5x + x - 1 = -52x = -5 + 12x = -4 x = -2Next thing to do would be to put value of x we got in equation (i) to get y
y - x = -1y - (-2) = -1 y + 3 = -1 y = -1 - 3 y = -4Values asked are :
\( \rightarrow \rm y = - 4\)
\( \rightarrow \rm x= - 2\)
`●.`●.`●.`●.`●.`●.`●.`●.`●.`●.`●.`●.`●.`●.`●.`●.`●.`●.
\( \large \bf hope \: \: it \: \: helps \: - dabI \)
`●.`●.`●.`●.`●.`●.`●.`●.`●.`●.`●.`●.`●.`●.`●.`●.`●.`●.
Which is the closest to the volume of the solid that remained?

Answers
Check the picture below.
so if we pluck the cylinder from the inside, what's leftover is that cyan ring with a height of 10, well, let's get the area of the ring and simply multiply it by its height.
\(\textit{area of a circular ring}\\\\ A=\pi (R^2 - r^2) ~~ \begin{cases} R=\stackrel{outer}{radius}\\ r=\stackrel{inner}{radius}\\[-0.5em] \hrulefill\\ R=15\\ r=11 \end{cases}\implies A=\pi (15^2-11^2)\implies A=104\pi \\\\[-0.35em] ~\dotfill\\\\ \stackrel{\textit{volume of a hollow cylinder}}{104\pi }\cdot 10 ~~ \approx ~~ \text{\LARGE 3267.26}~in^3 ~~ \approx 3266~in^3\)

Tom Jones, a mechanic at Golden Muffler Shop, is able to install new mufflers at an average rate of 3 per hour (exponential distribution). Customers seeking this service, arrive at the rate of 2 per hour (Poisson distribution). They are served first-in, first-out basis and come from a large (infinite population). Tom only has one service bay.
a. Find the probability that there are no cars in the system.
b. Find the average number of cars in the system.
c. Find the average time spent in the system.
d. Find the probability that there are exactly two cars in the system
Answers
a. To find the probability that there are no cars in the system, we need to use the formula for the steady-state probability distribution of the M/M/1 queue:
P(0) = (1 - λ/μ)
where λ is the arrival rate (2 per hour) and μ is the service rate (3 per hour).
P(0) = (1 - 2/3) = 1/3 or 0.3333
Therefore, the probability that there are no cars in the system is 0.3333.
b. To find the average number of cars in the system, we can use Little's Law:
L = λW
where L is the average number of cars in the system, λ is the arrival rate (2 per hour), and W is the average time spent in the system.
We can solve for W by using the formula:
W = 1/(μ - λ)
W = 1/(3 - 2) = 1 hour
Therefore, the average number of cars in the system is:
L = λW = 2 x 1 = 2 cars
c. To find the average time spent in the system, we already calculated W in part b:
W = 1 hour
d. To find the probability that there are exactly two cars in the system, we need to use the formula for the steady-state probability distribution:
P(n) = P(0) * (λ/μ)^n / n!
where n is the number of cars in the system.
P(2) = P(0) * (λ/μ)^2 / 2!
P(2) = 0.3333 * (2/3)^2 / 2
P(2) = 0.1111 or 11.11%
Therefore, the probability that there are exactly two cars in the system is 11.11%.
To know more about Poisson's Distribution:
https://brainly.com/question/9123296
#SPJ11
Can someone plz plz help me

Answers
Answer:
I have know clue
Step-by-step explanation:
do the data profvide evidnce that there is an association between age-group and whterher or not a person consumes five or more servings of fruits and vegetables per day for adults in hte united states?
Answers
The data provide convincing statistical evidence that there is an association between age group and consumption of fruits and vegetables for adults in the United States.
To determine if the data provide convincing statistical evidence that there is an association between age group and consumption of fruits and vegetables, we can perform a chi-squared test of independence. This test assesses whether there is a statistically significant association between two categorical variables.
The null hypothesis for this test is that there is no association between age group and consumption of fruits and vegetables, and the alternative hypothesis is that there is an association between the two variables.
Using the given data, we can calculate the expected frequencies for each cell under the assumption that there is no association between age group and consumption of fruits and vegetables. We can then use these expected frequencies to calculate the chi-squared test statistic and determine the p-value.
Performing the chi-squared test of independence with the given data yields a test statistic of 300.96 and a p-value of less than 0.0001. This indicates that there is a statistically significant association between age group and consumption of fruits and vegetables.
Learn more about the chi-squared test;
https://brainly.com/question/4543358
#SPJ4
The image of the complete question is given in the attachment.

Help!!!!!!!!! Quick!!!!!

Answers
Acute
Obtuse
Obtuse
Answer:
<A obtuse
<B acute
<C obtuse
<D right
Step-by-step explanation:
When calculating a nation’s digital power, what term is used to refer to the demonstrated capabilities of a nation-state in cyber offense or defense?
Answers
When calculating a nation’s digital power, the term that is used to refer to the demonstrated capabilities of a nation-state in cyber offense or defense is Cyberwarfare.
What is Cyberwarfare?Cyberwarfare can be regarded as the use of cyber attacks against a nation-state so as to produce significant harm.
It should be noted that Cyber Warfare is set of actions which is been carried out by nation or organization so as to be able to launch an attack on institutions' computer network systems.
The interests or reasons for cyberwarfares based on the Cybersecurity as well as Infrastructure Security Agency are;
To weaken the system of another country.To disrupt or destroy the sytem of another nation.In order to achieve the goals behind the cyberwarfare programs, it is usually designed to focus on spectrum of objectives which will bring harm to national interests.
Learn more about Cyberwarfare at:
https://brainly.com/question/13109173
#SPJ1
help please !!!! Please !!!!

Answers
Answer:
child byeee kid jdhuwkjikw
Step-by-step explanation:
Secondary School
The diagram shows a sector of a circle of radius 8 cm. The angle of the sector is x°.
The perimeter of the sector is (16+ 14pi)cm.
Find the value of x.
Answers
The angle of the sector is found to be 60 degrees.Given that the sector of a circle has a radius of 8 cm and its perimeter is (16 + 14π) cm. Let the angle of the sector be x°.
The perimeter of the sector can be expressed as the sum of the arc length and the lengths of the two radii. Therefore,
Perimeter of the sector = arc length + 2(radius)
(16 + 14π) = (x/360) * 2π * 8 + 2(8)
Simplifying the above equation, we get
16 + 14π = (4x/45)π + 16
14π = (4x/45)π
Dividing both sides by π, we get
14 = 4x/45
Multiplying both sides by 45, we get
630 = 4x
Therefore, x = 630/4 = 157.5 degrees.
However, we need to find the acute angle between the radii, which is half of the angle of the sector. Therefore, the angle of the sector is 2(157.5/2) = 157.5 degrees.
Hence, the angle of the sector is 60 degrees.
Learn more about perimeter here: brainly.com/question/30252651.
#SPJ11
How do I find the triangular formula of a pentagon
Answers
It is not possible to find the triangular formula of a pentagon because a pentagon is a polygon with five sides and does not have a triangular formula.
We have,
A triangular formula is used to calculate the area of a triangle, which is a polygon with three sides.
The formula for the area of a triangle is given by:
Area = 1/2 x base x height
where the base and height are two of the sides of the triangle.
If you want to calculate the area of a pentagon, you can use the formula for the area of a regular pentagon, which is given by:
Area = (5/4) x s² x tan(π/5)
where s is the length of one of the sides of the Pentagon.
Thus,
It is not possible to find the triangular formula of a pentagon because a pentagon is a polygon with five sides and does not have a triangular formula.
Learn more about the Pentagon here:
https://brainly.com/question/30182047
#SPJ1
Simplify using the Distributive Property (enter your answer with no
spaces) 2(6e - 3f + 10g)
Your answer
Answers
Answer:
2(6e-3f+10g)
Answer (I think): 12e-6f+20g
Step-by-step explanation:
Answer:
12e - 6f + 20g
Step-by-step explanation:
2(6e - 3f + 10g) is the given equation. Because of the grouping, we know that the entire part in parentheses is multiplied by two. Now the distributive property helps us by letting us multiply each individual part of the parentheses by two.
6e becomes 12e
-3f becomes -6f
and 10g becomes 20g
Now when we put those together, it becomes 12e - 6f + 20g
Hope this helped!
ATTENTION: TRY YOUR HARDEST AND ILL GIVE YOU BRAINLIEST!!!I need the most accurate answers, so only try if you know it: Ill give you brainliest x 4 if you are correct, for number 2 you need to do 1. A line goes through points (7, 3) and (-1,5). Write the equation of the line in POINT-Slope FORM. Show your work, so please hand write it, circle your answer! 2. A line goes through the points (7,3) and (-1,5). write the equation of the line in slope intercept form. Show your work so hand write it please, and attach it to your answer, circle your answer!. 3. Does the point (-4,3) fall on the graph of this line? (the line described in questions #1 and #2). How do you know? Show your work __________ALGEBRAICALLY. (That is, dont draw me a graph... show me using numbers, variables, and/or symbols). PLEASE TRY TO GET DONE TODAY ACCURATE ANSWERS ONLY

Answers
Answer:
waa ;-;
Step-by-step explanation:
sorry ill put it here monday
Answer:
;0
Step-by-step explanation:
hi
Solve the system of linear equations by graphing y=3/2x -1 and y=x
Answers
Answer:
x= 2 and y= 2
Step-by-step explanation:
y=3/2x -1 and y=x
Change x to y = 3 / 2x -1
x = 3/2x -1 and y=x
-1/2x = -1 and y=x
x= 2 and y= 2
45% of 30 is equal to 18% of what number
Answers
Answer:
75
Step-by-step explanation:
(0.45)(30) = (0.18)x
x = (0.45)(30) / (0.18)
x = 13.5 / 0.18 = 75
Check the answer:
(0.45)(30) = (0.18)(75)
13.5 = 13.5 answer is correct!
Answer:
Step-by-step explanation:
45% of 30 = 18% of some number
In this kind of questions, we usually assume the missing number as as something
Let the number be x
So assuming the number is x, the equation will be as follows:
45% of 30 is equal to 18% of x
45/ 100 * 30 = 18/100 * x
This means that 0.45 *30= 0.18 * x
Therefore, 13.5 = 0.18 x
Thus X = 13.5 / 0.18
Which is equal to 75
Thus 45% of 30 is equal to 18% of 75
Proving the above situation as follows:
45% OF 30 = 13.5
And 18% of 75 = 13.5
Thus both equations are equal.
Solution =75
Kayla is pricing whole wheat flour.
A 5-pound bag at Bargain Mart costs $6.45.
A 2-pound bag at Food Saver costs $2.50.
A 7-pound bag at Grocery Surplus costs $9.45
A 10-pound bag at Economart costs $12.89.
The shop with which sells flour for the lowest unit price is
Answers
Answer:
Food Saver
Step-by-step explanation:
6.45 ÷ 5 = 1.29
2.50 ÷ 2 = 1.25
9.45 ÷ 7 = 1.35
12.89 ÷ 10 = 1.289
Food Saver sells for $1.25 per pound, which is the lowest.
Answer:
Food Saver
Step-by-step explanation:
Bargain Mart: 6.45/5 = $1.29/lb
Food Saver: 2.50/2 = $1.25/lb
Grocery Surplus: 9.45/7 = $1.35/lb
Economart: 12.89/10 = $1.29/lb
Line AB and line BC form a right angle at point B. If A = (2, 5) and B = (4, 4), what is the equation of line BC?
Answers
Answer:
y = 2x - 4
Step-by-step explanation:
To solve this problem, we must first calculate the slope of the line AB using the formula:
\(\boxed{m = \frac{y_2 - y_1}{x_2 - x_1}}\)
where:
m ⇒ slope of the line
(x₁, y₁), (x₂, y₂) ⇒ coordinates of two points on the line
Therefore, for line AB with points A = (2, 5) and B = (4, 4) :
\(m_{AB} = \frac{5 - 4}{2 - 4}\)
⇒ \(m_{AB} = \frac{1}{-2}\)
⇒ \(m_{AB} = -\frac{1}{2}\)
Next, we have to calculate the slope of the line BC.
We know that the product of the slopes of two perpendicular lines is -1.
Therefore:
\(m_{BC} \times m_{AB} = -1\) [Since BC and AB are at right angles to each other]
⇒ \(m_{BC} \times -\frac{1}{2} = -1\)
⇒ \(m_{BC} = -1 \div -\frac{1}{2}\) [Dividing both sides of the equation by -1/2]
⇒ \(m_{BC} = \bf 2\)
Next, we have to use the following formula to find the equation of line BC:
\(\boxed{y - y_1 = m(x - x_1)}\)
where (x₁, y₁) are the coordinates of a point on the line.
Point B = (4, 4) is on line BC, and its slope is 2. Therefore:
\(y - 4 =2 (x - 4)\)
⇒ \(y - 4 = 2x - 8\) [Distributing 2 into the brackets]
⇒ \(y = 2x-4\)
Therefore, the equation of line BC is y = 2x - 4.
Write a word description of the set. {−5, −4, −3, −2, −1}
Answers
on a recent quiz, the class mean was 71 with a standard deviation of 4.2. calculate the z-score (to 4 decimal places) for a person who received score of 73.
Answers
The calculated value of z-score for the mean 71 and standard deviation 4.2 with person score 73 is equal to 0.4762( upto to four decimal place)
Mean of the data 'μ' = 71
Standard deviation of the data 'σ ' = 4.2
Score obtained by a person 'X' = 73
Formula for the z-score is equal to :
Z-score = ( X - μ ) / σ
Substitute the value of mean , standard deviation , and person score to get the value of z-score we have,
⇒ Z-score = ( 73 - 71 ) / 4.2
⇒ Z-score = ( 2 ) / 4.2
⇒ Z-score = 0.47619
⇒ Z-score = 0.4762
Therefore, the value of z-score as per the given mean and standard deviation is equal to 0.4762.
Learn more about z-score here
brainly.com/question/15016913
#SPJ4
Can someone please helpppp me!!

Answers
The specified circle's center is at (-7, 4). The revised center will therefore be (-7 - 3, 4 - 4) = (-10, 0).
What's the new centre of circle and new equation?We must deduct 3 from x and 4 from y in order to move the circle 3 units to the right and 4 units below. The revised center will therefore be (-7 - 3, 4 - 4) = (-10, 0).
By inserting the new center and simplifying, it is possible to find the equation for the resulting circle. The equation for a circle has the conventional form\((x - h)^2 + (y - k)^2 = r^2\), where (h, k) is the circle's center and r is its radius. Since the original equation is\((x+7)^2+(y-4)^2=36\), we may substitute the new center (-10, 0) and the radius 6 to obtain \((x + 10)^2 + y^2 = 36\)as the equation of the translated circle.
Learn more about quadratic equation here:
brainly.com/question/30098550
#SPJ1
