Answers
Answer:
x=6
Step-by-step explanation:
Because of the Pythagorean theorem, you know that the square of the two legs of a right triangle will be equal to the square of the hypotenuse. Conversely, the square of one of the legs will be equal to the square of the other leg subtracted from the square of the hypotenuse. Therefore:
\(x^2=10^2-8^2 \\\\x^2=100-64\\\\x^2=36\\\\x=6\)
Hope this helps!
Answer:
6
Step-by-step explanation:
By Pythagoras theorem
10^2 = 8^2 + x^2
100= 64 + x^2
X^2 =100-64
X^2= 36
\(x = \sqrt{36} \\ x = 6\)
Hope this helps..
Related Questions
find the sum of the geometric series given the following information
Answers
Answer:
-21844
Step-by-step explanation:
Finding n
aₙ = arⁿ⁻¹-16384 = -4(4)ⁿ⁻¹4ⁿ⁻¹ = 40964ⁿ⁻¹ = 64²4ⁿ⁻¹ = (8²)²4ⁿ⁻¹ = (4³)²n - 1 = 6n = 7Finding The Sum
S₇ = -4(4⁷ - 1) / 4 - 1S₇ = -4 (16383) / 3S₇ = -65536/3S₇ = -21844Answer:
-21844
Step-by-step explanation:
Given:
\(a_1=-4\)\(a_n=-16384\)\(r=4\)First find n by using the general form of a geometric sequence: \(a_n=ar^{n-1}\) (where a is the first term and r is the common ratio)
\(\implies -16384=(-4)(4)^{n-1}\)
\(\implies 4^{n-1}=\dfrac{-16384}{-4}\)
\(\implies 4^{n-1}=4096\)
\(\implies \ln 4^{n-1}=\ln 4096\)
\(\implies (n-1)\ln 4=\ln 4096\)
\(\implies n=\dfrac{\ln 4096}{\ln 4}+1\)
\(\implies n=6+1\)
\(\implies n=7\)
Sum of the first n terms of a geometric series:
\(S_n=\dfrac{a(1-r^n)}{1-r}\)
(where a is the first term and r is the common ratio)
Substituting the given values and the found value of n into the formula:
\(\implies S_{7}=\dfrac{(-4)(1-4^7)}{1-4}\)
\(\implies S_{7}=-21844\)
Write an expression for the length of the rectangle. (Hint: Factor the area binomial and recall that Area = width x length.)

Answers
the other side of the rectangle \(x^{4} - 8x\).
What is a rectangle?
Rectangles are quadrilaterals having four right angles in the Euclidean plane of geometry. Various definitions include an equiangular quadrilateral, A closed, four-sided rectangle is a two-dimensional shape. A rectangle's opposite sides are equal and parallel to one another, and all of its angles are exactly 90 degrees. Area of rectangle is A = a*b
The area of the given figure \(4x^{5} - 32x\)
one side given is 4x.
So the other side will be \(4x^{5} - 32x\) / 4x
=4x(\(x^{4} - 8x\))/4x
=\(x^{4} - 8x\)
Hence the other side of the rectangle \(x^{4} - 8x\).
Learn more about rectangular by following the link below.
brainly.com/question/25292087
#SPJ1
Please write well.
Answer the following question when X₁, X₂,..., X is a random sample from an exponential family with the following probability density function. f(x 0) = exp (0T(x) + d(0)+ S(x)) a. H: 0= 0 vs H₁
Answers
Given that X₁, X₂,..., X is a random sample from an exponential family with the following probability density function, f(x 0) = exp (0T(x) + d(0)+ S(x)).
To form the hypothesis for the exponential family, we need to consider the null and alternative hypothesis.
Null hypothesis: 0= 0
Alternative hypothesis: 0 ≠ 0
Explanation: The exponential family is a class of distribution families. The density of an exponential family is given by the following expression:
f(x|θ) = h(x) exp{θT(x) − A(θ)},
where h(x) is a nonnegative function of the data that does not depend on the parameter θ and A(θ) is a normalizing function.
The parameter θ is typically called the natural parameter, and T(x) is the vector of sufficient statistics. The exponential family of distributions includes the normal, exponential, chi-squared, gamma, and beta distributions, among others. In hypothesis testing for the exponential family, we typically specify a null hypothesis and an alternative hypothesis, just as in other types of hypothesis testing. The test statistic is usually a ratio of two likelihood ratios.
To know more about exponential family refer to:
https://brainly.com/question/27622986
#SPJ11
A rock is tossed from a platform and follows a parabolic path through the air. The height of the rock in metres is given by h(t) = -5t² + 12t + 14 where t is measured in seconds. a) How high is the rock off the ground when it is thrown? b) How long is the rock in the air? c) For what times is the height of the rock greater than 17 metres? d) How long is the rock above the height of 17 metres?
Answers
Given information:h(t) = -5t² + 12t + 14 where t is measured in seconds.a) How high is the rock off the ground when it is thrown?For h(0), the initial height of the rock is required.h(0) = -5(0)² + 12(0) + 14 = 14 meters.
For h(t), the rock's maximum height needs to be found to determine the time when the rock hits the ground. In order to determine the maximum height, first, we need to find the time of maximum height using the formula:
tmax = -b/2a = -12/2(-5) = 1.2s
Now, h(1.2) can be found to determine the maximum height:
h(1.2) = -5(1.2)² + 12(1.2) + 14 = 20.8 meters
Therefore, the rock is in the air for (1.2*2) 2.4 seconds.c) For what times is the height of the rock greater than 17 metres?This means h(t) > 17. Solving this inequality gives:-
5t² + 12t + 14 > 17
=> -5t² + 12t - 3 > 0
=> (-5t + 3)(t - 1) > 0
From part c, we know that the rock's height is greater than 17 metres between 0 and 0.6 seconds and after 1 second. Therefore, the time the rock is above 17 metres is the sum of these two time periods:0.6 seconds + (2 - 1) seconds = 1.6 seconds.
To know more about inequality visit:-
https://brainly.com/question/28823603
#SPJ11
write the linear equation in slope intercept form: 5x + y= -17
x= -1/5y - 17/5
y= -5x - 17
y= -5x + 17
y= 5x - 17
Answers
Answer:
\(y = - 5x + 17\)
Step-by-step explanation:
\(i n \: slope \: intercept \: form \: y = mx + c \\ for \: the \: \: liear \: equaton = 5x + y = 17 \\ y = - 5x + 17\)
The function s(m)=5+4(m−1) represents the number of stamps in Rudy’s stamp collection in month m. What does the value 4 represent in this situation?
a. Rudy's collection is worth $4.
b. Rudy collected stamps for 4 months.
c. Rudy began his collection with 4 stamps.
d. Rudy adds 4 more stamps to his collection every month
Answers
The value 4 in the function s(m) = 5 + 4(m-1) represents the number of stamps Rudy adds to his collection every month. Therefore, the correct answer is d) Rudy adds 4 more stamps to his collection every month.
In the given function, s(m), m represents the number of months Rudy has been collecting stamps. The expression (m-1) represents the number of months minus one, indicating that the calculation starts from the second month. The coefficient 4 represents the number of additional stamps Rudy adds to his collection each month. For example, if we substitute m = 2 into the function, we get s(2) = 5 + 4(2-1) = 5 + 4(1) = 9. This means that after the second month, Rudy's collection would have 9 stamps in total, indicating the addition of 4 more stamps. Therefore, the value 4 in the given function represents the number of stamps Rudy adds to his collection every month.
learn more about addition here:
https://brainly.com/question/29783548
#SPJ11
Please help me I’m very confused!!

Answers
first off let's keep in mind that an absolute value is really a ± equation in disguise, so |5x -4| can pretty much be rewritten as ±(5x - 4), so is a dual equation, let's solve both for "x".
\(|5x-4|\leqslant 3x\implies \pm(5x-4)\leqslant 3x \\\\[-0.35em] ~\dotfill\\\\ +(5x-4)\leqslant 3x\implies 5x-4\leqslant 3x\implies 2x-4\leqslant 0\implies 2x\leqslant 4 \\\\\\ x\leqslant \cfrac{4}{2}\implies {\LARGE \begin{array}{llll} x\leqslant 2 \end{array}} \\\\[-0.35em] ~\dotfill\)
\(-(5x-4)\leqslant 3x\implies (5x-4)\stackrel{\stackrel{notice}{\downarrow }}{\geqslant} -3x\implies 8x-4\geqslant 0 \\\\\\ 8x\geqslant 4\implies x\geqslant \cfrac{4}{8}\implies {\LARGE \begin{array}{llll} x\geqslant \cfrac{1}{2} \end{array}}\)
Check the picture below.

Which relation does not represent a function?

Answers
Answer:
horizontal line because it doesn't pass vertical line test
If you answer this you get brainliest

Answers
Please help. SINE=?

Answers
Answer: opposite/hypotenuse
Step-by-step explanation:
i need a answer asap please

Answers
Answer:
g=92°
h=88°
m=89°
k=91°
Step-by-step explanation:
Answer:
h=88 g=92 m=89 k=91
Step-by-step explanation:
180-92=88
180-91=89
I'm not 100% certain about g and k, because I haven't done this in a while, but I'm pretty sure opposite angles equal the same thing. Also, a line is 180 degrees so just subtract the 180 from the number in the angle on the same line.
PLEASE HURRY!!
A cone has a height of 7 ft and a radius of 4 ft. Which equation can find the volume of the cone?
V=52172(4382
v-264217)ft
V = 3x(72)(4) ft
V-37(42)(7)ft?
Answers
Answer:
V = π*r^2*h/3
the formula not sure which answer represent that
117.29 ft^3
Step-by-step explanation:
The production cost to make 10 shirts is modeled by the expression 1.By + 5.5, where y represents the number of meters of fabric needed to make the shirts. Which
expression represents the production cost for one shirt?
A.0.18y +0.55
B.0.18y +5.5
C.1.8y +0.55
D.18y +55y
Answers
Answer:
The answer is 0.18y+5.5
Step-by-step explanation:
because the only thing you had to do is move the decimal.
The expression which represents the production cost for one shirt is, 0.18y +0.55. So Option A is correct
What are expressions?An expression is a sentence with at least two numbers or variables having mathematical operation. Math operations can be addition, subtraction, multiplication, division.
For example, 2x+3
Given that,
The production cost to make 10 shirts is modeled by the expression,
Total Cost = 1.8y + 5.5,
where y represents the number of meters of fabric needed to make the shirts
So, for one shirt cost,
Cost of 1 shirt = Total Cost/10
= 1.8y + 5.5/10
= 0.18y + 0.55
Thus, the expression is 0.18y + 0.55
To know more about Expressions check:
brainly.com/question/16804733
#SPJ6
find the value of x.
2+3
12
5
1.2
6.6
07
12

Answers
Answer:
x = 7
Step-by-step explanation:
The triangles are similar
12/8 = (x+3+5)/(x+3) cross multiply expressions
12x + 36 = 8x + 64
12x - 8x = 64 - 36
4x = 28 divide both sides by 4
x = 7
A spherical balloon is being filled with air at the constant rate of 8 cm? sec How fast is the radius increasing when the radius is 6 cm? Submit an exact answer in terms of T. Provide your answer below: cm sec
Answers
A spherical balloon is being filled with air at the constant rate of 8 cm³/sec How fast is the radius increasing when the radius is 6 cm?
Rate of change of radius of sphere 0.0176 cm/sec.
A spherical balloon is filled with air at the constant rate of 8 cm³/sec.
Formula used: Volume of sphere = (4/3)πr³
Differentiating both sides with respect to time 't', we get: dV/dt = 4πr²dr/dt, where dV/dt is the rate of change of volume of a sphere, and dr/dt is the rate of change of radius of the sphere.
We know that the radius of the balloon is increasing at the constant rate of 8 cm³/sec. When the radius is 6 cm, then we can find the rate of change of the volume of the sphere at this instant. Using the formula of volume of a sphere, we get: V = (4/3)πr³
Substitute r = 6 cm, we get: V = (4/3)π(6)³ => V = 288π cm³ Differentiating both sides with respect to time 't', we get: dV/dt = 4πr²dr/dt, where dV/dt is the rate of change of volume of sphere, and dr/dt is the rate of change of radius of the sphere. Substitute dV/dt = 8 cm³/sec, and r = 6 cm,
we get:8 = 4π(6)²(dr/dt)
=>dr/dt = 8/144π
=>dr/dt = 1/(18π) cm/sec
Therefore, the radius is increasing at the rate of 1/(18π) cm/sec when the radius is 6 cm.
Rate of change of radius of sphere = 1/(18π) cm/sec= 0.0176 cm/sec.
Learn more about the volume of a sphere: https://brainly.com/question/22716418
#SPJ11
Write 15+45 as a product of 2 factors using GCF and the distributive property
Answers
We can write (15 + 45) as a product of 2 factors using GCF and the distributive property 15(1 + 3).
We are given the following expression-
15 + 45
Now, we can factorize 15 into prime factors as follows -
= 3 × 5 (15 × 1)
Similarly, we can factorize 45 into prime factors as follows -
= 3 × 3 × 5 (15 × 3)
Thus, the greatest common factor of 15 and 45 is 15, so we can
= 15 × 1 = 15 and 15 × 3 is 45
Hence, we can write (15 + 45) as 15(1 + 3).
Learn more about the distributive property:
brainly.com/question/28490348
#SPJ4
If -3x + 5 > 4, which of the following cannot be a value of x? 7.11B-S)
A -3
B -1
C о
D 4
Answers
Answer:
D
Step-by-step explanation:
Solving the inequality
- 3x + 5 > 4 ( subtract 5 from both sides )
- 3x > - 1
Divide both sides by - 3, reversing the symbol as a result of dividing by a negative value.
x < \(\frac{1}{3}\)
The only value not less than \(\frac{1}{3}\) is 4 → D
How do you do this???
Given tan Ф = 4/5, find all other trig functions.
Answers
let : y = Opponent side, x= Adjecent side
and r= hypotenuse
tan = 4/5
y/x = 4/5 => y =4, x=5
so, r = √4²+5²=√16+25=√41
sin = y/r = 4/ √41
cos = x/r = 5/√41
tan = y/x = 4/5
csc = r/y = √41 /4
sec = r/x = √41 /5
cot = x/y = 5/4
Lilla's water bottle has some water in it already, but she wants to completely fill it up before going to practice. She adds 21 ounces of water to completely fill the 40-ounce bottle. Write an equation to represent the situation.
Answers
The diameter of a circle is 7 m. Find its area to the nearest tenth.
Answers
Area = pi x r^2
R = 7/2 = 3.5
Area = 3.14 x 3.5^2
Area = 38.5 m^2
38.5
Step-by-step explanation:
A = pi*r^2
A = pi*3.5^2
A = pi*12.25
A = 38.465
Question 6 of 10
Which factor increases risk while driving a car because it interferes with
attention?
O A. Not wearing a seat belt
B. Drowsiness
C. Driving in the middle lane
OD. Driving in the right lane
SUBMIT
Answers
The area of a triangle is 3232. Two of the side lengths are 74 and 94 and the included angle is acute. Find the measure of the included angle, to the nearest tenth of a degree.
Answers
If im not wrong it would be 12 degrees
Find the circumference of the object. Use 3.14 or 22/7 for Pi. Round to the nearest hundredth if necessary.

Answers
Answer:
\(43.96 \text{ in}\)
Step-by-step explanation:
The equation for circumference is:
\(C=2\pi r\)
Using the diagram, we can conclude that the radius of the object is 7 in.
We can substitute this value in for the equation (Note that I will use 3.14 for π):
\(C=2\pi r\\C=2*3.14*7\\C=14*3.14\\C=43.96\text{ in}\)
at a point on the ground 50 meters from the foot of a tree, the angle of elevation of the top of the tree is 48 degrees. find the height of the tree to the newest hundredth of a meter.
Answers
When measured from a position on the ground 50 meters away from a tree, the height of the tree is 55.5 meters to the nearest hundredth of a meter.
what is trigonometry ?The association between triangle line angle lengths and angles is examined in the mathematics discipline known as trigonometry. The application of geometry in astronomical inquiry gave rise to the area's first appearance in the 18th century, roughly in the third centuries BC. Exact approaches mathematics focuses on certain right triangle and how they could be applied to operations. In trigonometry, there are six well-known trigonometric functions. They are identified by their various names and buzzwords: sine, cosine, parallel, cotangent, hyperbolic tangent, and cosecant (csc). Trigonometry is the study of the properties of triangles, particularly of right triangles. The features of all geometric forms are studied in geometry.
given
Base = 50, Elevation Angle = 48
An angle's opposite or adjacent side is its tan.
Tan (48),
height/distance, = 50*tan (48),
height, or 55.5 feet.
When measured from a position on the ground 50 meters away from a tree, the height of the tree is 55.5 meters to the nearest hundredth of a meter.
To know more about trigonometry visit:
https://brainly.com/question/29002217
#SPJ1
Hannah either walks or cycles to school. The probability that she walks to school is 0.75. If she walks, the probability that she is late is 0.6. If she cycles, the probability that she is late is 0.2. Work out the probability that on any one day Hannah will not be late for school

Answers
Answer:
0.17
Step-by-step explanation:
im not really sure but that closest as 0.75+0.6+0.2=0.83 and 1.00-0.83=0.17
Answer:
0.17
hope this helps
Can anyone help me with this question please ? I’ll mark as brainliest.

Answers
Answer:
f (x) = - 11 ( \(7^{x-1}\))
Step-by-step explanation:
( x , y )
( 1 , - 11 )
( 2 , - 11 × 7 )
( 3 , - 11 × 7 × 7 )
( 4 , - 11 × 7 × 7 × 7 )
( x , - 11 × \(7^{x-1}\) )
f (x) = - 11 ( \(7^{x-1}\))
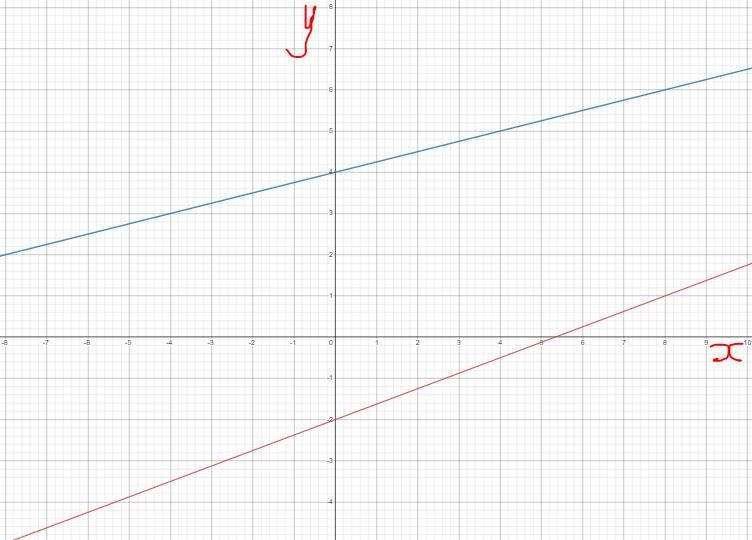
lines a and b are a graph of a system of equations line a passes through the points (0,4) and (8,6) line b passes through the points (0,-2) and (8,1) do the intersect
Answers
The graph of line a and line b is shown in the image attached below. The lines do not intersect each other.
How to Graph a System of Equations?To check if both lines intersect, we need to graph the system of equations. First, use the points given to write out the equations.
Line a:
Slope (m) = change in y / change in x = 6 - 4 / 8 - 0 = 2/8
m = 1/4
Find the y-intercept (b) by substituting m = 1/4, x = 0 and y = 4 into y = mx + b:
4 = 1/4(0) + b
b = 4
The equation of line a is: y = 1/4x + 4.
Line b:
Slope (m) = change in y / change in x = 1 - (-2) / 8 - 0
m = 3/8
Find the y-intercept (b) by substituting m = 3/8, x = 0 and y = -2 into y = mx + b:
-2 = 3/8(0) + b
b = -2
The equation of line b is: y = 3/8x - 2.
Both lines are graphed in the image attached below. Line a is the red line and line b is the red line. They do not intersect at any point.
Learn more about graph of system of equations on:
https://brainly.com/question/14323743
#SPJ1
Luke cut down a tree that was 26.4 feet tall then he cut six equal pieces to take it away What is the length of each piece
Answers
Express the cubed root of a cubed root of the cubed root of 2 with a rational index.
Answers
Answer:
\(2^{\frac{1}{27} }\)
Step-by-step explanation:
→ Write in number format
∛∛∛2
→ Rewrite
\(2^{\frac{1}{3} } *2^{\frac{1}{3} } *2^{\frac{1}{3} }\)
→ Simplify
\(2^{\frac{1}{27} }\)
Answer:
2^(1/27).
Step-by-step explanation:
That would be [(2)^1/3)^1/3]^1/3
= 2^1/3*1/3*1/3)
= 2^(1/27)
What is the value of the expression 2x² – 5x + 6 when
x = -2?
Answers
Answer:
24 is correct answer
Step-by-step explanation:
\(2 {x}^{2} - 5x + 6 \\ = 2 {( - 2)}^{2} - 5 \times ( - 2) + 6 \\ = 2 \times 4 + 10 + 6 \\ = 8 + 10 + 6 \\ = 24\)
hope it helped you:)
