Answers
Answer:
Step-by-step explanation:
x+94 = 4x+25
69 = 3x
x = 23°
Related Questions
an airplane flew for one hour and landed 100 miles north and 80 miles east from its origin. what was the distance traveled, speed and angle of direction from its origin?
Answers
The distance traveled by airplane is 180 miles.
The speed of the airplane is 3 miles per minute and the angle of direction from the origin is 51.34°
The airplane landed 100 miles north and 80 miles east from its origin and it flew for one hour.
Then, the total distance traveled by airplane will be:
= 100 miles + 80 miles = 180 miles.
The speed can be defined as the distance traveled by the total time taken.
Speed = distance/time
Speed = 180 miles/ 1 hour
Speed = 180 miles/60 minutes
Speed = 3 miles per minute
The angle of direction from its origin will be:
tan (x) = 100 miles/80 miles
x = tan⁻¹ ( 100/80)
x = tan⁻¹ ( 10/8) = tan⁻¹ ( 5/4)
x = 51.34°
Learn more about speed here:
brainly.com/question/13943409
#SPJ1
Find the midpoint between the pair of points. (-1, -5) and (-5, 9)
Answers
Answer:
Step-by-step explanation:
(-1-5)/2 = -6/2= -3
(-5+9)/2 = 4/2 = 2
(-3, 2)
2x - 7 + 3x = 4x + 2 need help with this one
Answers
Answer:
x = 9
Step-by-step explanation:
To solve the equation 2x - 7 + 3x = 4x + 2 for x, you can follow these steps:
Combine like terms on both sides of the equation. Add the x terms together and move the constant terms to one side of the equation:
2x + 3x - 4x = 2 + 7
Simplifying the left side: x = 9
Simplify the right side of the equation:
x = 9
Therefore, the solution to the equation is x = 9.
solve it and show full calculus.
thank you!

Answers
Answer:
Hi
Please mark brainliest ❣️
Thanks
Step-by-step explanation:
The answer is NO
Reason
x= 2 y= 1
Now input in the first inequality
y≤ -x + 4
1 ≤ -2 +4
1≤ 2 i.e 1 is less than two
Next inequality
y≤ x +1
1 ≤ 2 + 1
1≤ 3 i.e 1 is less than 3
But 1 is not equal to 3 and also not equal to 2
Hence our answer is NO
write an equation of the line that passes through (-1, 4.5) and (1, -1.5)
Answers
A cube has edge length 3 in. What is its volume?
Answers
The volume of a cube is given by the formula V = s^3, where s is the length of one of its sides. So, if the edge length of a cube is 3 inches, its volume would be:
V = 3^3 = 27 cubic inches
Your neighbor has a bag with 5 oranges and 7 apples in it. You will be receiving two pieces of fruit from your neighbor. What is the probability, in percent, that you will receive 2 apples, assuming she removes them from the bag in random order
Answers
Answer:
31.82% probability that you will receive 2 apples.
Step-by-step explanation:
The fruits are removed from the bag, which means that the hypergeometric distribution is used to solve this question.
Hypergeometric distribution:
The probability of x sucesses is given by the following formula:
\(P(X = x) = h(x,N,n,k) = \frac{C_{k,x}*C_{N-k,n-x}}{C_{N,n}}\)
In which:
x is the number of sucesses.
N is the size of the population.
n is the size of the sample.
k is the total number of desired outcomes.
Combinations formula:
\(C_{n,x}\) is the number of different combinations of x objects from a set of n elements, given by the following formula.
\(C_{n,x} = \frac{n!}{x!(n-x)!}\)
In this question:
5 + 7 = 12 total fruits, which means that \(N = 12\)
7 apples, which means that \(k = 7\)
You receive 2 fruits, which means that \(n = 2\)
What is the probability, in percent, that you will receive 2 apples, assuming she removes them from the bag in random order?
This is, as a proportion, P(X = 2). So
\(P(X = x) = h(x,N,n,k) = \frac{C_{k,x}*C_{N-k,n-x}}{C_{N,n}}\)
\(P(X = 2) = h(2,12,2,7) = \frac{C_{7,2}*C_{5,0}}{C_{12,2}} = 0.3182\)
0.3182*100% = 31.82%
31.82% probability that you will receive 2 apples.
An article contained the following observations on degree of polymerization for paper specimens for which viscosity times concentration fell in a certain middle range:
420 425 427 427 432 433 434 437 439 446 447 448 453 454 465 469
Suppose the sample is from a normal population.
(a) Calculate a 95% confidence interval for the population mean, and interpret it.
(b) Calculate a 95% upper confidence bound for the population mean, and interpret it.
Answers
Answer:
(a) A 95% confidence interval for the population mean is [433.36 , 448.64].
(b) A 95% upper confidence bound for the population mean is 448.64.
Step-by-step explanation:
We are given that article contained the following observations on degrees of polymerization for paper specimens for which viscosity times concentration fell in a certain middle range:
420, 425, 427, 427, 432, 433, 434, 437, 439, 446, 447, 448, 453, 454, 465, 469.
Firstly, the pivotal quantity for finding the confidence interval for the population mean is given by;
P.Q. = \(\frac{\bar X-\mu}{\frac{s}{\sqrt{n} } }\) ~ \(t_n_-_1\)
where, \(\bar X\) = sample mean = \(\frac{\sum X}{n}\) = 441
s = sample standard deviation = \(\sqrt{\frac{\sum (X-\bar X)^{2} }{n-1} }\) = 14.34
n = sample size = 16
\(\mu\) = population mean
Here for constructing a 95% confidence interval we have used One-sample t-test statistics as we don't know about population standard deviation.
So, 95% confidence interval for the population mean, \(\mu\) is ;
P(-2.131 < \(t_1_5\) < 2.131) = 0.95 {As the critical value of t at 15 degrees of
freedom are -2.131 & 2.131 with P = 2.5%}
P(-2.131 < \(\frac{\bar X-\mu}{\frac{s}{\sqrt{n} } }\) < 2.131) = 0.95
P( \(-2.131 \times {\frac{s}{\sqrt{n} } }\) < \({\bar X-\mu}\) < \(2.131 \times {\frac{s}{\sqrt{n} } }\) ) = 0.95
P( \(\bar X-2.131 \times {\frac{s}{\sqrt{n} } }\) < \(\mu\) < \(\bar X+2.131 \times {\frac{s}{\sqrt{n} } }\) ) = 0.95
95% confidence interval for \(\mu\) = [ \(\bar X -2.131 \times {\frac{s}{\sqrt{n} } }\) , \(\bar X +2.131 \times {\frac{s}{\sqrt{n} } }\) ]
= [ \(441-2.131 \times {\frac{14.34}{\sqrt{16} } }\) , \(441+2.131 \times {\frac{14.34}{\sqrt{16} } }\) ]
= [433.36 , 448.64]
(a) Therefore, a 95% confidence interval for the population mean is [433.36 , 448.64].
The interpretation of the above interval is that we are 95% confident that the population mean will lie between 433.36 and 448.64.
(b) A 95% upper confidence bound for the population mean is 448.64 which means that we are 95% confident that the population mean will not be more than 448.64.
Given the sequence: 1;x; 6;y:15 ... The sum of the first four terms is 20 and the second differences are equal 1.1 Find a formula for the nth term Tn
Answers
9514 1404 393
Answer:
Tn = (n/2)(n +1)
Step-by-step explanation:
The first differences are ...
x -1, 6 -x, y -6, 15 -y
Then the second differences are ...
(6 -x) -(x -1) = 1 ⇒ 7 -2x = 1 ⇒ x = 3
(y -6) -(6 -x) = 1 ⇒ x + y = 13 ⇒ y = 10
(15 -y) -(y -6) = 1 ⇒ 21 -2y = 1 ⇒ y = 10
Then the sequence is ...
1, 3, 6, 10, 15, ...
which is the sequence of triangle numbers. The formula for the general term is ...
Tn = (n/2)(n +1)
Answer:
Step-by-step explanation:
Here is a methode more general:
\(\Delta_{1,n}=u_{n+1}-u_{n}\\\\\Delta_{1,n+1}=u_{n+2}-u_{n+1}\\\\\\\Delta_{2,n}=\Delta_{1,n+1}-\Delta_{1,n}=u_{n+2}-u_{n+1}-(u_{n+1}-u_{n})\\=u_{n+2}-2*u_{n+1}+u_{n}=1\\\\\Delta_{2,n+1}=u_{n+3}-2*u_{n+2}+u_{n+1}=1\\\\\Delta_{2,n+1}-\Delta_{2,n}=u_{n+3}-3*u_{n+2}+3u_{n+1}-u_n=0\\\\Caracteristic\ equation: \ r^3-3r^2+3r-1=0=(r-1)^3\\\\u_n=k_1*1^n+k_2*n*1^n+k_3*n^2*1^n\\\\\)
\(\left\{\begin{array}{ccc}u_1&=&1\\u_2&=&x\\u_3&=&6\\\end {array}\right.\\\\\\\left\{\begin{array}{ccc}k_1+k_2+k_3&=&1\\k_1+2*k_2+4*k_3&=&x\\k_1+3*k_2+9*k_3&=&6\\\end {array}\right.\\\\\\\left\{\begin{array}{ccc}k_1&=&-3x+9\\\\k_2&=&4x-\dfrac{23}{2}\\\\k_3&=&-x+\dfrac{7}{2}\\\end {array}\right.\\u_n=-3x+9+(4x-\dfrac{23}{2})*n+(-x+\dfrac{7}{2})*n^2\\\\u_1=-3x+4x-x+9-\dfrac{23}{2} +\dfrac{7}{2} =1\\u_2=-3x+8x-4x+9-23 +14=x\\u_3=-3x+12x-9x+9-\dfrac{69}{2} +\dfrac{63}{2} =6\\\)
\(u_4=-3x+16x-16x+9-46 +56 =-3x+19=y\\u_5=-3x+20x-25x+9-\dfrac{115}{2} +\dfrac{175}{2} =-8x+39=15\\\\\Longrightarrow\ x=3\\k_1=-9+9=0\\k_2=4*3-\dfrac{23}{2} =\dfrac{1}{2}\\k_3=-3+\dfrac{7}{2} =\dfrac{1}{2}\\\\\\u_n=0+\dfrac{n}{2}+\dfrac{n^2}{2}=\dfrac{n*(n+1)}{2}\\\\Sequence\ is\ 1;3;6;10;15;...\\\)
The density d of a substance is given by the formula d = m/v, where m is its mass and V is its volume.
Pyrite is
Density: 5.01g/cm
Volume: 1.2cm.
a. Solve the formula for m.
m=
b. Find the mass of the pyrite sample.
The mass is grams.
Answers
Step-by-step explanation:
a. d = m/v
m = d × v
b. m = d × v
= 5.01g/cm × 1.2cm
= 6.012g
hopefully this makes sense
:)
The mass of pyrite sample in grams will be - 6.012 grams
We have a marble whose volume is 1.2 cubic centimeter and density is 5.01 g/cm. A relation - density d of a substance is given by the formula
d = m/v is also provided.
We have to determine its mass.
Which state of matter has the highest density? Explain why?The solid state of matter has the highest density because the constituent particles are fixed and not allowed to move inside the solid. Moreover, they are bonded very close to each other.
According to the question -
Density - 5.01g/cm
Volume - 1.2cm.
Using the formula mentioned above, we get -
\($\rho = \frac{M}{V}\)
Rearranging the formula, we get -
M = ρV
M = 5.01 x 1.2 = 6.012 grams
Hence, the mass of pyrite sample in grams will be - 6.012 grams
To solve more questions on Volume - density relation, visit the link below -
brainly.com/question/24439891
#SPJ2
Bronson is ordering a sundae at a restaurant, and the server tells him that he can have up to four toppings: butterscotch sauce, caramel, peanuts, and strawberries. Since he cannot decide how many of the toppings he wants, he tells the server to surprise him. If the server randomly chooses which toppings to add, what is the probability that Bronson gets just butterscotch sauce, peanuts, and strawberries
Answers
Answer:
20%
Step-by-step explanation:
if zero toppings is an option, then there would be 5 possibilities for toppings
0,1,2,3,or 4
the server randomly chose 3 toppings so that would be one out of 5 or 20%.
(If the server did not have the option to put zero toppings on then there would be only 4 options 1,2,3, or 4 toppings and the correct answer would be one out of 4 or 25%.)
Represent the following expression using an exponent
12.12.12.12
Options are:
12⁴
1⁴
4¹²
1¹²
Answers
Find u+v-4u.
u=(5,-2) and v= (-5,7)
Answers
By placing the given value in equation , we get u + v - 4u = (-20, 13)
How to evaluate vector?A physical quantity that has both directions and magnitude is referred to as a vector quantity.
A lowercase letter with a "hat" circumflex, such as "û," is used to denote a vector with a magnitude equal to one. This type of vector is known as a unit vector.
To evaluate u + v - 4u, we first need to find the vector 4u, which is obtained by multiplying the vector u by the scalar 4:
4u = 4(5,-2) = (20,-8)
Now, we can add u and v, and subtract 4u from the result:
u + v - 4u = (5,-2) + (-5,7) - (20,-8)
= (5 - 5 - 20, -2 + 7 + 8)
= (-20, 13)
Therefore, u + v - 4u = (-20, 13).
To know more about vector visit:
https://brainly.com/question/29740341
#SPJ1
Part A: Timothy said that AKLM was dilated by a scale factor of 1.5 centered at the origin. Is Timothy CORRECT? Explain your answer or show your work.

Answers
Yes, Timothy is correct because triangle AKLM was dilated by using a scale factor of 1.5 centered at the origin.
What is dilation?In Mathematics, dilation can be defined as a type of transformation that is typically used for enlarging or reducing the size of a geometric object but not its shape, based on the scale factor.
For the given coordinates of the preimage triangle KLM, the dilation with a scale factor of 1.5 from the origin (0, 0) would be calculated as follows:
Coordinate K (-1, 3) → Coordinate K' (-1 × 1.5, 3 × 1.5) = Coordinate K' (-1.5, 4.5).
Coordinate L (8, 4) → Coordinate L' (8 × 1.5, 4 × 1.5) = Coordinate L' (12, 6).
Coordinate M (10, -3) → Coordinate M' (10 × 1.5, -3 × 1.5) = Coordinate M' (15, -4.5).
In conclusion, the coordinates of the image triangle K'L'M after a dilation with a scale factor of 1.5 from the origin are (-1.5, 4.5), (12, 6), and (15, -4.5) as shown in the graph above, therefore, Timothy is correct.
Read more on dilation here: brainly.com/question/20482938
#SPJ1
From the expression below select the one that results in a negative difference.

Answers
Explanation: Math.
Explanation:Math^^^
What is the first quartile of the data displayed in this box-and-whisker plot?
143.0
43.5
99.5
113.0

Answers
Answer:
The first quartile is 99.5
Step-by-step explanation:
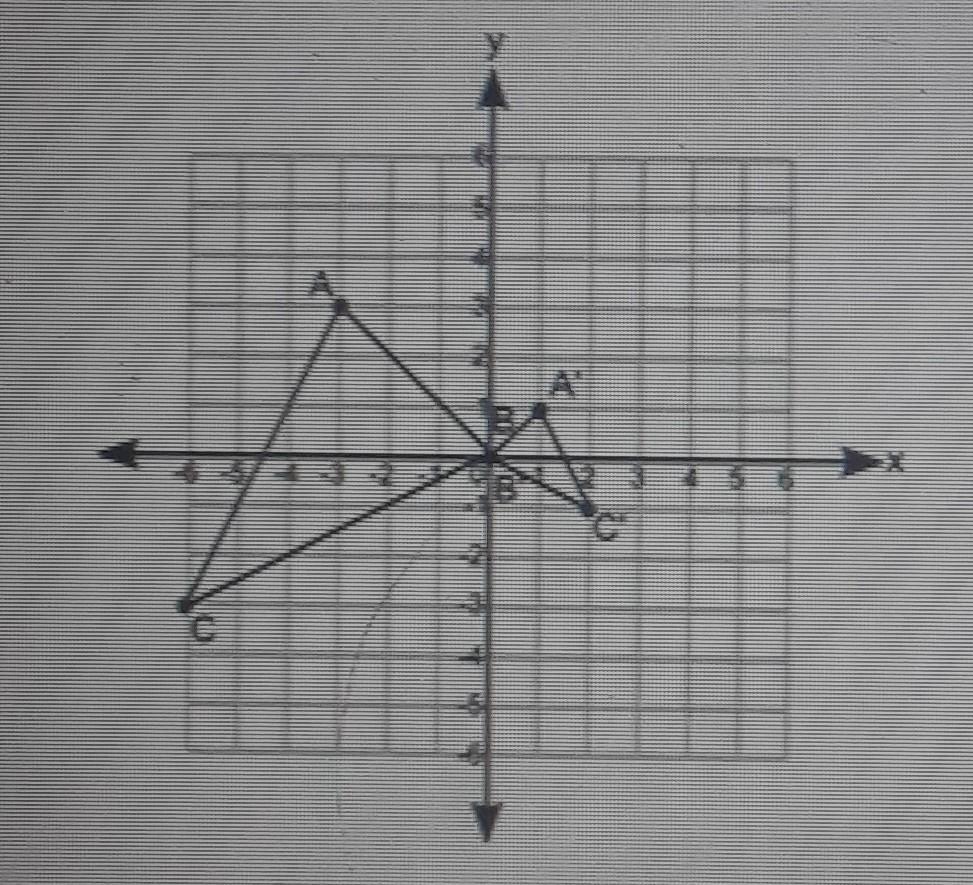
the Firgure shows two triangles on a coordinate grid: Which set of transformations have been performed on triangle ABC to form triangle A'B'C'? A) Dilation by a scale factor of 1/3 followed by reflection about the x-axisB) Dilation by a scale factor of 3 followed by reflection about the x-axis C) Dilation by a scale factor of 1/3 followed by reflection about the y-axis D) Dilation by a scale factor of 3 followed by reflection about the y-axis
Answers
In transformations, the Pre-Image is the original figure and the Image is the figure transformated.
In this case you can identify that the Pre-Image is the triangle ABC and the Image is the triangle A'B'C'.
Notice that the vertices of ABC are:
\(A(-3,3);B(0,0);C(-6,-3)\)By definition, when the scale factor used in the dilation is between 0 and 1, the Image obtained is a reduction and, therefore, it is smaller than the Pre-Image. Since A'B'C' is smaller than ABC, then you can determine that ABC was dilated by this scale factor:
\(sf=\frac{1}{3}\)When a figure is reflected across the y-axis, the rule is:
\((x,y)\rightarrow\mleft(-x,y\mright)\)If you dilate ABC by the scale factor shown above, and then you reflect it across the y-axis, the coordinates of the Image will be:
\(\begin{gathered} A\mleft(-3,3\mright)\rightarrow A^{\prime}(-(\frac{-3}{3}),\frac{3}{3})\rightarrow A^{\prime}(1,1) \\ \\ B\mleft(0,0\mright)\rightarrow B^{\prime}\mleft(0,0\mright) \\ \\ C\mleft(-6,-3\mright)\rightarrow C^{\prime}(-(\frac{-6}{3}),\frac{-3}{3})\rightarrow C^{\prime}(2,-1) \end{gathered}\)Notice that the coordinates of A'B'C' shown in the picture match with the vertices found above.
Therefore, the answer is: Option C.
Consider the sets below. U = {x| x is a real number} A = (x x is an odd integer} R = {x | x = 3, 7, 11, 27) IsRC A? • yes, because all the elements gf set A are in set R O yes, because all the elements of set R are in set A • no, because each element in set A is not represented in set R • no, because each element in set R is not represented in set A
Answers
Set A and Set R do not have one-to-one correspondence in terms of their elements. Therefore, the correct answer is no, because each element in set R is not represented in set A.
Set A is defined as the set of odd integers, while set R is defined as the set containing the elements 3, 7, 11, and 27. Since set R contains specific elements, it is not possible for every element in set A to be represented in set R.
For example, there are odd integers such as 5, 9, and 13 that are not included in set R. On the other hand, if the question was asking if set A is a subset of set R, then the answer would be no as well.
A subset relationship implies that every element in set A is also in set R, but since set R contains specific elements (3, 7, 11, 27), it does not include all the odd integers.
To learn more about integers
https://brainly.com/question/929808
#SPJ8
The piecewise function represents the amount of taxes owed, f(x), as a function of the taxable income, x. Use the marginal tax rate chart or the piecewise function to answer the questions.
Tax Bracket Marginal Tax Rate
$0–$10,275 10%
$10,276–$41,175 12%
$41,176–$89,075 22%
$89,076–$170,050 24%
$170,051–$215,950 32%
$215,951–$539,900 35%
> $539,901 37%
A piecewise function f of x in seven pieces. The function is defined by part 1, which is 0 point 10 times x for x less than or equal to 10,275; part 2, which is 0 point 12 times x minus 205 point 50 for 10,276 is less than or equal to x which is less than or equal to 41,175; part 3 which is 0 point 22 times x minus 4,323 for 41,176 is less than or equal to x which is less than or equal to 89,075; part 4 which is 0 point 24 times x minus 6,105 point 50 for 89,076 is less than or equal to x which is less than or equal to 170,050; part 5 which is 0 point 32 times x minus 9,070 point 32 for 170,051 is less than or equal to x which is less than or equal to 215,950; part 6 which is 0 point 35 times x minus 26,187 point 50 for 215,951 is less than or equal to x which is less than or equal to 539,900; and part 7 which is 0 point 37 times x minus 36,985 point 67 for x is greater than or equal to 539,901.
Part A: Using the method of your choice, demonstrate how to calculate the amount of taxes owed on a taxable income of $31,000. Show all work. (4 points)
Part B: Using the taxes owed from part A, determine the effective tax rate. Show all work. (4 points)
Part C: Compare the piecewise function to the marginal tax rate chart. How is the marginal tax rate chart represented in the piecewise function? (2 points)
Answers
Answer:
Part A: $3,415.50
B: 11.34%
Step-by-step explanation:
Part A: $31,000 is within the values 10,276≤x≤41,175, so use f(x)=0.12x-205.50
Part B: For the effective tax rate, divide the amount in part A by the taxable income
Part C: Compare both the taxable income and the effective tax rate to the income domains given and the % multiplier. This one is mostly about how you describe the situation, so I'll leave that up to you.
To calculate the taxes owed on a taxable income of $31,000, we use the appropriate equation for the tax bracket it falls into and substitute the value of x. The effective tax rate is calculated by dividing the amount of taxes owed by the taxable income and multiplying by 100. The piecewise function represents the marginal tax rate chart by using different equations for each tax bracket.
Explanation:Part A:
To calculate the amount of taxes owed on a taxable income of $31,000, we need to determine which tax bracket it falls into. Since $31,000 is greater than $10,275 but less than $41,175, it falls into tax bracket 2. To find the amount of taxes owed, we use the equation for tax bracket 2: f(x) = 0.12x - 205.50. Plugging in $31,000 for x, we get:
f(x) = 0.12 * 31000 - 205.50 = $3,574.50
Therefore, the amount of taxes owed on a taxable income of $31,000 is $3,574.50.
Part B:
To determine the effective tax rate, we divide the amount of taxes owed by the taxable income. Using the result from Part A (taxes owed = $3,574.50) and the taxable income of $31,000, we have:
Effective tax rate = (taxes owed / taxable income) * 100 = (3,574.50 / 31,000) * 100 ≈ 11.52%
Therefore, the effective tax rate on a taxable income of $31,000 is approximately 11.52%.
Part C:
The piecewise function represents the amount of taxes owed as a function of the taxable income. Each part of the function corresponds to a different tax bracket, with the equation for that tax bracket. The marginal tax rate chart is represented in the piecewise function by the different equations for each tax bracket. For example, the equation in part 1 of the function (f(x) = 0.10x) corresponds to the 10% marginal tax rate for the tax bracket $0-$10,275.
Learn more about Taxes Calculations here:
https://brainly.com/question/16200743
#SPJ2
5. You buy a boat for $35,000 that * 10 points
depreciates in value at about 17%
per year. How much will it be worth
in 3 years?
Your answer
Answers
Answer:
9000
Step-by-step explanation:
3. An investor plans to invest $500/year and expects to get a 10.5% return. If the investor makes these contributions at the end of the next 20 years, what is the present value (PV) of this investment today?
Answers
The present value (PV) of the investment today is approximately $2,965.05.
To find the present value (PV) of the investment today, we need to calculate the present value of each individual contribution and then sum them up. We can use the formula for the present value of an annuity to do this calculation.
The formula for the present value of an annuity is given by:
PV = C * [(1 - (1 + r)^(-n)) / r]
Where:
PV = Present Value
C = Cash flow per period
r = Interest rate per period
n = Number of periods
In this case, the cash flow per period (C) is $500, the interest rate per period (r) is 10.5% (or 0.105), and the number of periods (n) is 20 years.
Let's plug in these values into the formula and calculate the present value (PV):
PV = $500 * [(1 - (1 + 0.105)^(-20)) / 0.105]
Using a calculator, we can evaluate the expression inside the brackets:
PV = $500 * [(1 - 0.376889) / 0.105]
Simplifying further:
PV = $500 * [0.623111 / 0.105]
PV = $500 * 5.930105
PV = $2,965.05
Therefore, the present value (PV) of the investment today is approximately $2,965.05.
for such more question on present value
https://brainly.com/question/28256489
#SPJ8
Solve (x – 3)2 = 49. Select the values of x. –46 -4 10 52
Answers
Answer:10
Step-by-step explanation:
If anyone is good in Pythagoras theoram please help me
Answers
Answer:
a^2+B^2=c^2
Step-by-step explanation:
Step-by-step explanation:
(Hyp)² = (Base)² + (Height)²
C² = a² + b²
C= √a²+b²
This is the formula to find Hypotenuse of a right angled triangle
3. What is the proper ordering
(from greatest to least) of the
following numbers?
I.58/67
II.0.58%
III.58%
IV.5.8%
O I, III, II,
O III, IV, II, I
O I, III, IV, II
O IV, I, III, II
Answers
Answer:
C) I, III, IV, II
Step-by-step explanation:
Convert each number into a decimal:
\(\textsf{I.} \quad \dfrac{58}{67}=0.86567...\)
\(\textsf{II.} \quad 0.58\%=\dfrac{0.58}{100}=0.0058\)
\(\textsf{III.} \quad 58\%=\dfrac{58}{100}=0.58\)
\(\textsf{IV.} \quad 5.8\%=\dfrac{5.8}{100}=0.058\)
Comparing the tenths of all the numbers, 8 is the biggest tenth, so 58/67 is the largest number.
The next biggest tenth is 5, so 58% is the next largest number.
The two remaining numbers have zero tenths, so compare their hundredths. 5 is the largest hundredth, so 5.8% is the next largest number. Therefore, 0.58% is the smallest number.
Therefore, the given set of numbers in order from greatest to least is:
I, III, IV, IIAnswer:
c) I, III, IV, II
Step-by-step explanation:
Values of l, ll, lll & lV respectively,
→ 58/67, 0.58%, 58%, 5.8%
→ 0.87, 0.0058, 0.58, 0.058
Arranging them in descending order,
→ 0.87 > 0.58 > 0.058 > 0.0058
→ 0.87, 0.58, 0.058, 0.0058
→ l, lll, lV, ll
Hence, the option (c) is correct.
Consider triangle XYZ with altitude WZ. What is XZ?
X
W
N
28
21
Y

Answers
The value for the side of rectangle XZ is equal 14, using the trigonometric ratios of cosine and sine of angles.
What is trigonometric ratios?The trigonometric ratios concerns the relationship of an angle of a right-angled triangle to ratios of two side lengths. The basic trigonometric ratios includes;
sine, cosine and tangent.
Considering the triangle WYZ, the cosine of angle Y;
cos(Y) = 21/YZ {adjacent/hypotenuse}
YZ = [21/cos(Y)] {cross multiply}
Considering the triangle XYZ, the cosine of angle Y;
cos(Y) = YZ/28
YZ = 28 × cos(Y)
Therefore,
28cos(Y) = [21/cos(Y)]
cos²(Y) = 21/28 {cross multiply}
cos(Y) = √(21/28) {take the square root of both sides}
cos(Y) = 0.8660
Y = cos^(-1)(0.8660) {cross multiply}
Y = 30°
To get the side XZ, considering the triangle XYZ the sine of 30°;
sin30° = XZ/28 {opposite/hypotenuse}
by cross multiplication
XZ = 28 × sin30°
XZ = 14
Therefore, by proper application of the trigonometric ratios of cosine and sine of the angle for the given triangle, the side XZ = 14.
Know more about trigonometric ratios here:https://brainly.com/question/27976417
#SPJ1
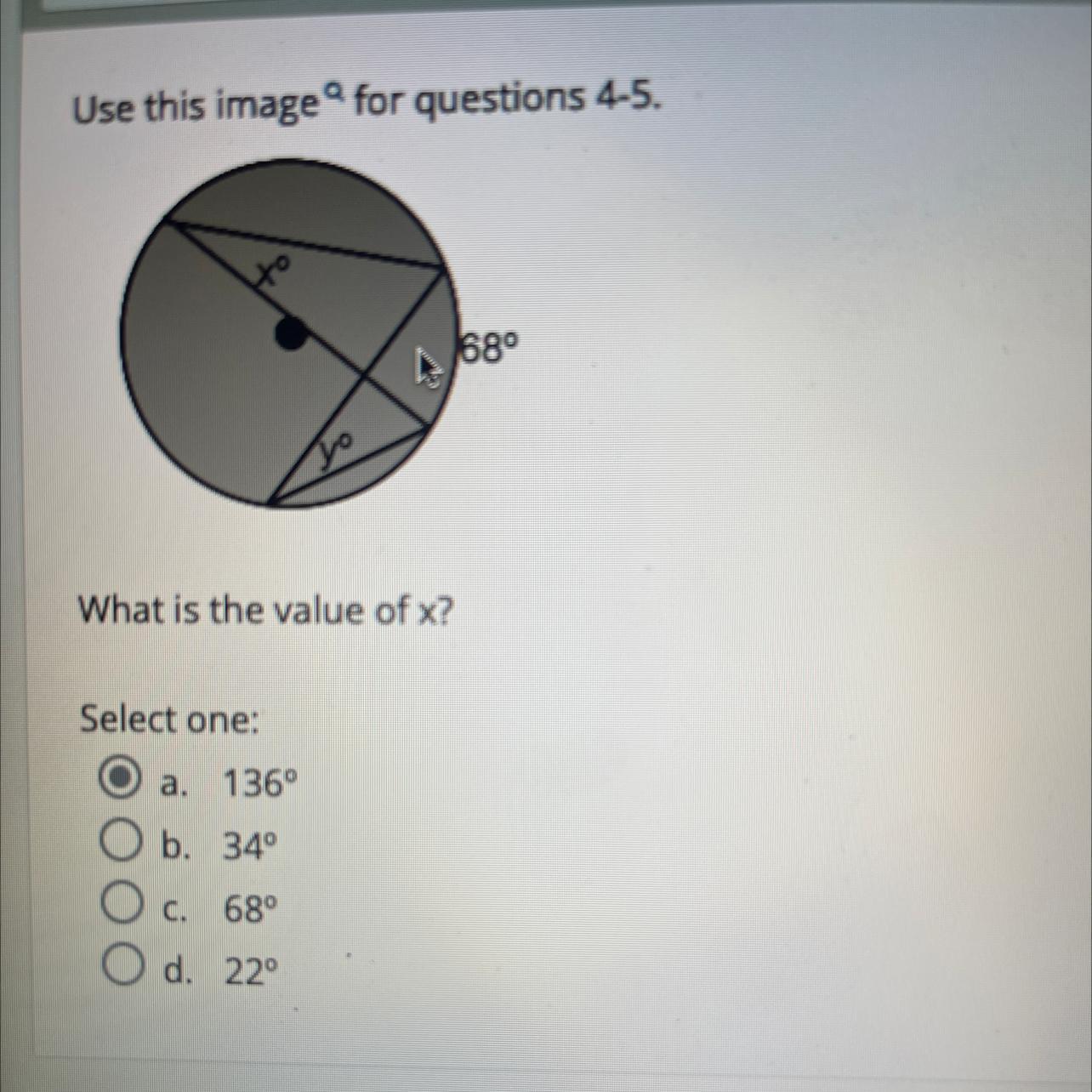
What is the value of x?
Answers
The value of x is 34 degree.
The correct option is B.
We have the measure of arc = 68 degree
We know,
angle at Center = Arc
and, Angle on circle= Arc/2
So, Angle on Arc= 68/2
Angle on Arc= 34 degree
Thus, the value of x is 34 degree.
Learn more about arc here:
https://brainly.com/question/31612770
#SPJ1
Ivanna received a $70 gift card for a coffee store. She used it in buying some coffee that cost $7.31 per pound. After buying the coffee, she had $26.14 left on her card. How many pounds of coffee did she buy?
Answers
the first time in my class or must i forget abt u cos i always indoors and i know ukuthi im not strong so
Who is your favorite y-o-u-t-u-b-e-r
Answers
Answer:
dream
Step-by-step explanation:
why not
Answer:
Mine is 5 minute crafts
I love crafts, so ya. They are pretty popular
please give me brainiest :) !
The figure below shows roads near a pond. Each segment of the triangle represents a road or a path, except AB which represents the distance across the pond. Are the two triangles similar?

Answers
Answer:
Yes, triangles ABC and DEC are similar by AA. Angles ABC and DEC are congruent, and angles ACB and DCE are congruent.
2/3 ounce servings are in 5 1/2 ounces of oatmeal
Answers
Answer: 4/33
Step-by-step explanation:
just divide
Answer:
The answer is 4/33.
Step-by-step explanation:
to get this you just have to divide.
you're welcome.
