PLEASE HELP FAST
decide if the following systems of equations have a single solution no solution or infinity many solution x+ 5y =9 _ x+5y=6
Answers
Answer:
no solutions
Step-by-step explanation:
I believe there are no solutions for these 2 equations.
Hope this helps!
Related Questions
Anaya is viewing her bank account online. She sees 3 entries for Monday, each for $10.50. Write an expression to represent the total change in Anaya's account on Monday.

Answers
Answer: 3 • (-10.50)
Step-by-step explanation:
it told me bc i got it wrong lol
The expression for total change in Anaya's account on Monday is \(-10.50\times 3\) or \(3\times (-10.50)\).
Important information:
Anaya sees 3 entries for Monday, each for \(-\$10.50\).Expression:Value of one entry is \(-\$10.50\).
It means, the change in account by one entry is \(-\$10.50\).
The value of three entries is the product of the value of one entry and 3.
\(-10.50\times 3\)
Therefore, the expression for total change in Anaya's account on Monday is \(-10.50\times 3\) or \(3\times (-10.50)\).
Find out more about 'Expression' here:
https://brainly.com/question/25301924
Someone please help with my STAT homework PLEASE I will give brainliest

Answers
Hi there!
a. A stratified sample can be used by dividing the tenants into two groups: those who have children and those who do not have children. Then, a Sample Random Sample FROM EACH stratum can be conducted for a total of 16 tenants surveyed.
b. Using a cluster sample in this situation could introduce undercoverage or selection bias if there is a distinction between those on some floors and those on others. For example, tenants on lower floors might be more opposed to a playground (ex: noise, crowd, etc.) in comparison to those on higher floors.
Cindy and her family are at the movies and wish to purchase some popcorn. A large popcorn costs $8 and a small popcorn costs $4. Cindy has offered to pay for the popcorn with the $23 in her wallet.
Write the inequality in standard form that describes this situation. Use the given numbers and the following variables.

Answers
The inequality in standard form that describes Cindy's situation as required is; 8x + 4y ≤ 23.
Which inequality correctly describes Cindy's situation?It follows from the task content that the inequality which correctly describes the situation is to be determined.
Since: x = no. of large popcorns and y = no. of small popcorns;
The required inequality is;
8x + 4y ≤ 23.
This follows from the fact that; Cindy can only spend a maximum of $23.
Read more on inequalities;
https://brainly.com/question/25275758
#SPJ1
For approximately what values of x can you replace sin x by x − x^3/6 with an error of magnitude no greater than 6×10^−4?
Answers
With an error of magnitude no more than 6×10^−4, the values of x for which sin x can be replaced by x - x^3/6 are roughly: -0.3728 ≤ x ≤ 0.3728
To find the values of x for which sin x can be replaced by x - x^3/6 with an error of magnitude no greater than 6×10^−4, we need to analyze the Taylor series expansion of sin x around x = 0. The Taylor series for sin x is:
sin x = x - x^3/6 + x^5/120 - x^7/5040 + ...
We are given the approximation sin x ≈ x - x^3/6, which corresponds to the first two non-zero terms of the Taylor series. To find the error bounds, we consider the next term in the series, x^5/120. To have an error no greater than 6×10^−4, we need:
|x^5/120| ≤ 6×10^−4
Now, solve for x:
|x^5| ≤ 72×10^−4
|x| ≤ (72×10^−4)^(1/5)
Calculating the fifth root gives:
|x| ≤ 0.3728
Therefore, the values of x for which sin x can be replaced by x - x^3/6 with an error of magnitude no greater than 6×10^−4 are approximately:
-0.3728 ≤ x ≤ 0.3728
Learn more about "sin x": https://brainly.com/question/15287659
#SPJ11
find the radius of convergence, r, of the series. [infinity] n = 1 (−1)nxn 7 n
Answers
The radius of convergence, denoted as r, of the series ∑(n=1 to infinity) (-1)^n * x^n / 7^n is 7.
The radius of convergence can be determined using the ratio test, which states that for a power series ∑(n=0 to infinity) a_n * (x - c)^n, if the limit of the absolute value of (a_(n+1) / a_n) as n approaches infinity exists, then the series converges if the limit is less than 1 and diverges if the limit is greater than 1.
In this case, a_n = (-1)^n / 7^n, and we can apply the ratio test:
|(-1)^(n+1) * x^(n+1) / 7^(n+1)| / |(-1)^n * x^n / 7^n| = |x / 7|
As n approaches infinity, the absolute value of (x / 7) remains constant. Thus, for the series to converge, |x / 7| < 1, which implies that |x| < 7. Therefore, the radius of convergence is 7.
Note that the endpoints of the interval of convergence should be checked separately to determine if the series converges at those points.
To learn more about radius of convergence click here: brainly.com/question/31440916
#SPJ11
what's an equation represents the line that is perpendicular to y = 5 x + 4 and passes through the point (- 5,2)
Answers
Equation of the line
The equation of a line in slope-intercept form is:
y = mx + b
Where m is the slope and b is the y-intercept.
We are required to find the equation of a line that is perpendicular to the line
y = 5x + 4
and passes through the point (-5,2)
The first thing we need to do is to calculate the slope of the required line.
The slope of the given line is m1=5. Two lines are perpendicular if their slopes satisfy the equation:
m1 * m2 = -1
Solving for m2:
\(m_2=-\frac{1}{m_1}=-\frac{1}{5}\)The equation of the required line is:
\(y=-\frac{1}{5}x+b\)To find the value of b, we substitute the given point (-5,2):
\(2=-\frac{1}{5}(-5)+b\)Operating:
\(2=1+b\)Solving for b:
b = 1
Finally, our equation is:
\(y=-\frac{1}{5}x+1\)Factor: 3(5x+2)(5x-2)
Answers

Please answer rather quickly, it’s a math question
What triangle makes the statement true? DEF=__
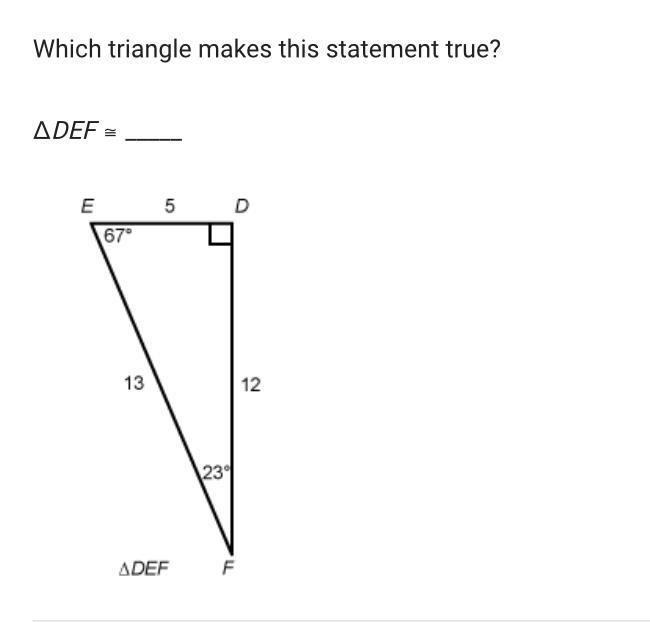

Answers
Answer:
c: triangle ABC is congruent to DEF
Step-by-step explanation:
find the triangle with the same side lengths and angle measurements to the given triangle.
The true statement is DEF= ABC
Thus, option (C) is correct.
As, per the figure Triangle DEF.
<DFE= 23
<DEF = 67
<EDF = 90
ED= 5 unit
EF = 13 unit
DF = 12 unit
Now, to find the congruent triangle to DEF.
Look for the triangle which same angles and sides as triangle DEF.
So, In Triangle ABC.
<CBA= 23
<CBA = 67
<BAC = 90
AB= 5 unit
CB= 13 unit
CA= 12 unit
Therefore, the statement is DEF= ABC
Thus, option (C) is correct.
Learn more about Congruency here:
https://brainly.com/question/31992651
#SPJ4
salik: we need two quantitative variables for this project. wouldn’t number of siblings be categorical since it is whole numbers?
Answers
Salik and Maya are discussing a project that examines the relationship between the number of siblings someone has and their household income. Maya predicts that those with more siblings will have a higher household income. Salik questions whether the number of siblings is a categorical variable since it is a whole number. Our response can be : "In order to conduct this project, we need to choose two quantitative variables, which are variables that can be measured and expressed as numbers. The number of siblings is not a categorical variable because it is a continuous variable that can take on any whole number value."
The number of siblings is a quantitative variable because it can be expressed as a whole number. Household income is also a quantitative variable because it can be measured and expressed as a numerical value. Categorical variables are variables that can be divided into distinct categories or groups, such as gender, race, or occupation. The number of siblings is not a categorical variable because it is a continuous variable that can take on any whole number value.
To examine the relationship between the number of siblings and household income, Maya and Salik could use statistics to analyze their data. They could calculate descriptive statistics such as the mean and standard deviation for each variable, as well as the correlation coefficient to determine the strength and direction of the relationship between the two variables. They could also use probability theory to make predictions about the likelihood of certain outcomes, such as the probability that someone with more siblings will have a higher household income.
The complete question is:
Our classmates, Maya and Salik, are talking about the variables they want to study and how they plan to collect their samples. Here is part of their conversation. Respond in the places that say “your response.”
Double-check that both of their variables are quantitative.
Maya: I want to look at the relationship between the number of siblings someone has and the household income. I predict that those with more siblings have a higher household income.
Salik: We need two quantitative variables for this project. Wouldn’t number of siblings be categorical since it is whole numbers?
Your response:.........
Learn more about descriptive statistics at : https://brainly.com/question/28686879
#SPJ11
What is mFGH?
A.-39 degrees
B. -52 degrees
C.-78 degrees
D.- 141 degrees

Answers
Answer:
78
Step-by-step explanation:
You add 115 and 167 which will give you 282.
Subtract 282 from 360, which will equal 78.
What unit of measure provides the best estimate?
A thick literature book can weigh up to 3 __
A: oz
B: lb
C: T
D: ft
Answers
B: lb (pounds)
Pounds (lb) is a common unit of measure for weight, and it would provide a more suitable estimate compared to ounces (oz), tons (T), or feet (ft), which are units of measure for different quantities such as length or volume.
Answer:
B: lb
Step-by-step explanation:
Why not A?
The book can't measure ounces, because that is a liquid measure.
Why not C?
It can't measure tonne, because that would be 100 pounds. Who would make a literature book that weighs 100 pounds?! The heaviest book weighs 37.5 pounds
Why not D?
A thick literature book can't 'weigh' feet, that is a height measure.
A middle school took all of its 6th grade students on a field trip to see a ballet at a theater that has 1300 seats. The students filled 1001 of the seats in the theater. What percentage of the seats in the theater were filled by the 6th graders on the trip?
Answers
I like to use ratios and cross multiply for problems like this. Take the part (1001) over the whole (1300), and that equals x percent of 100 percent.
1001/1300 = x/100
100100 = 1300x
x = 77
Show that the helium ground state wavefunction Ψ(1,2)= 2
1
1s(1)1s(2)[α(1)β(2)−β(1)α(2)] is normalised, that is, show that ∬[Ψ(1,2)] 2
dτ 1
dτ 2
=1 The integration variable dτ is a product of the volume dv and spin dγ variables.
Answers
The helium ground state wavefunction Ψ(1,2) = 2√(1s(1)1s(2)[α(1)β(2)−β(1)α(2)]) is normalized.
How can we show that the integral of Ψ(1,2) squared over all variables equals 1?To show that the wavefunction Ψ(1,2) is normalized, we need to calculate the integral of Ψ(1,2) squared over all variables and demonstrate that the result is equal to 1.
The integral is given by:
\(∬[Ψ(1,2)]^2 dτ₁dτ₂\),
where dτ₁ is the volume element for particle 1, dτ₂ is the volume element for particle 2, and dτ = dv dγ is the product of the volume dv and spin dγ variables.
To simplify the integral, we can first square the wavefunction Ψ(1,2) and then integrate over the spatial and spin coordinates. Since the spin variables are orthogonal, the spin part of the integral will evaluate to 1.
The spatial part of the integral can be calculated by considering the overlap of the hydrogenic 1s orbitals for both particles.
This overlap depends on the inter-particle distance and can be solved using the radial wavefunction for the 1s state. After performing the integration, we find that the spatial part evaluates to 1/2.
Multiplying the spatial part by the spin part, we obtain a final result of 1/2 * 1 = 1, demonstrating that the wavefunction Ψ(1,2) is normalized.
Learn more about wavefunction
brainly.com/question/29089081
#SPJ11
14) Acacia is trying to decide whether to purchase a new sofa and armchair using an installment credit offer from the store or to wait until she has enough cash saved to buy the living room furniture without relying on credit. The total cost of the furniture is $2,700. The installment credit offer requires that Acacia pay 17% per year for the loan. She may pay interest only for the first year of the loan. Assuming that Acacia would pay only the interest for the first year and then pay off the principal, how much more would she end up paying for the furniture than if she waits until she has enough saved up to pay for it in cash? *
Answers
Answer:
Acacia is trying to decide whether to purchase a new sofa and armchair using an installment credit offer from the store or to wait until she has enough cash ...
Step-by-step explanation:
The requreid Acacia would have to pay $459 in interest for the first year of the installment credit offer.
What is simple interest?Simple interest is a quick and simple formula for figuring out how much interest will be charged on a loan.
SI = Principal×rate×time
If Acacia chooses to take the installment credit offer, she will only pay the interest for the first year. The interest payment for the first year can be calculated as:
Interest = Principal x Rate x Time
where Principal is the amount borrowed, Rate is the interest rate per year, and Time is the time period in years.
Here, Principal is $2,700 and Rate is 17% per year. Since Acacia only pays interest for the first year, Time is 1 year.
So, Interest = 2700 x 0.17 x 1 = $459
Therefore, Acacia would have to pay $459 in interest for the first year of the installment credit offer.
If she chooses to wait until she has enough saved up to pay for the furniture in cash, she would not have to pay any interest. Therefore, she would save $459 by waiting to buy the furniture in cash.
Learn more about simple interests here:
https://brainly.com/question/26457073
#SPJ2
Which of the following is NOT a solution to the system of inequalities? Please help
A) (1, 5)
B) (2, 1)
C) (1, 2)
D) (0, 4)

Answers
Answer:
B (It isn't in the shaded region)
In a volatile housing market, the overall value of a home can be modeled by V(x)=325x^2-4600x+145000, where v represents the value of the home and x represents each year after 2020. Find the vertex and interpret what the vertex of this function means in terms of the value of the home.
Answers
The vertex of the quadratic function foer the value of a home, and the interpretation of the vertex are;
Vertex; (7.08, 128,723.08)
The vertex can be interpreted as follows; In the yare 2027, the value of a nome will be lowest value of $128723.08
What is a quadratic function?A quadratic function is a function of the form; f(x) = a·x² + b·x + c, where a ≠ 0, and a, b, and c are numbers.
The model for the value of a home, V(x) is; V(x) = 325·x² - 4600·x + 145,000, where;
v = The value of the home
x = The year after 2020
The vertex of the function can be obtained from the x-coordinates at the vertex of a quadratic function, which is; x = -b/(2·a), where;
a = The coefficient of x², and
b = The coefficient of x
Therefore, at the vertex, we get;
x = -(-4600)/(2 × 325) = 92/13 ≈ 7.08
Therefore, the y-coordinate of the vertex is; V(x) = 325×(92/13)² - 4600×(92/13) + 145,000 ≈ 128,723.08
The vertex is therefore; (7.08, 128,723.08)
The interpretation of the vertex is as follows;
Vertex; (7.08, 128,723.08)The year of the vertex, x ≈ 7 years
The value of a home at the vertex year is about; $128,723
The positive value of the coefficient a indicates that the vertex is a minimum point
The vertex indicates that the value of a home in the market will be lowest in about 7 years after 2020, which is 2027
Therefore, at the vertex, after about 7 years the value of a home will be lowest at about $1228,723Learn more on the vertex of quadratic functions here: https://brainly.com/question/31241321
#SPJ1
Let's denote a lottery as (X₁, P₁; X2, P2; ; Xm, Pm), where Xi and Pi indicate the reward magnitude = and probability of each potential outcome. A decision-maker prefers B ($5000, 1.00) to A = ($0, 0.01; $25000, 0.04; $5000, 0.95) and prefers C = ($25000, 0.04; $0, 0.96) to D = ($5000, 0.05; $0, 0.95). Prove that Expected Utility Theory cannot account for the preference. Note: you can assume that the initial endowment is $0 and the utility of $0 is zero.
Answers
Thus, even if the expected value of option A is higher than the expected value of option B, EUT cannot account for the preference.
Expected Utility Theory (EUT) asserts that a decision-maker's utility function can be used to predict their preferences between uncertain options.
If a decision-maker has an ordered preference ranking of lotteries, according to EUT, these rankings would correspond to their expected utility rankings.
Nevertheless, some examples demonstrate that EUT may fail to predict preferences. Let's denote a lottery as
(X₁, P₁; X2, P2; ; Xm, Pm),
where Xi and Pi indicate the reward magnitude and probability of each potential outcome.
A decision-maker prefers B ($5000, 1.00) to
A = ($0, 0.01; $25000, 0.04; $5000, 0.95) and prefers
C = ($25000, 0.04; $0, 0.96) to
D = ($5000, 0.05; $0, 0.95).
However, EUT cannot account for these preferences.
The utility of the three alternatives is calculated as follows:
U(B) = $5000
U(C) = 0.04 × $25,000 + 0.96 × $0 = $1,000
U(D) = 0.05 × $5000 + 0.95 × $0 = $250
However, the expected utilities of A and B cannot be compared.
These preferences might instead be clarified using theories like Rank-Dependent Expected Utility Theory.
to know more about Expected Utility Theory visit:
https://brainly.com/question/28289214
#SPJ11
how to convert m to cm?
Answers
Answer:
You multiply by 100
Step-by-step explanation:
1 m = 100 cm
How to convert m to cm?
You multiply by 100
Select the equation in point-slope form for the line that passes through (3, - 5) and has a slope of 2.
Answers
Answer:
..Step-by-step explanation:
What is the slope of the line that passes through (2, 3) and has a y-intercept of -1?
Answers
If each soda sells for $2.50, what is the expected daily total dollar amount taken in by the vendor from the sale of sodas?
Answers
Answer:
$34.38
Step-by-step explanation:
Y: A random variable that indicates the amount of money that the seller will receive.
p=2,50$
if x=0 → y=0.2,50=0$
if x=5 → y=5.2,50 = 12,5 $
if x=10 → y=10.2,50= 25$
if x=15 → y=15.2,50= 37,5$
if x=20 → y=20.2,50= 50 $
if x=25 → y=25.2,50= 62,5$
Y= { 0$ ; 12,5$ ; 25$ ; 37,5$ ; 50$ ; 62,5$ }
E(Y)= ∑Y.P(Y)
= 0.P(0)+12,5.P(12,5)+ 25.P(25)+ 37,5.P(37,5)+ 50.P(50)+ 62,5.P(62,5)
= 0.0,01+ 12,5.0,15+ 25.0,25+ 37,5.0,3+ 50.0,25+ 62,5.0,04
= 0 + 1,875 + 6,25 + 11,25 + 12,5 + 2,5
= 34,38$ expected value of the amount of money the seller receives.
Need help ASAP please I’ll give you a brainliest

Answers
Answer: 159.428571429??????
Step-by-step explanation:
I hope im not wrong (sorry im not always correctt)
the answer is below PLEASE HELP IM BEING TIMED I WILL MARK BRAINLIEST IF RIGHT

Answers
Here is the work:

What are the solutions to the quadratic equation (2b+3)^2=12

Answers
Answer:
b=− 3/4 =−1.333
b= 2/3=1.500
explanation
middle term, which is -1 .
-72 + 1 = -71
-36 + 2 = -34
-24 + 3 = -21
-18 + 4 = -14
-12 + 6 = -6
-9 + 8 = -1 That's it
Two real solutions:
b =(1+√289)/12=(1+17)/12= 1.500
or:
b =(1-√289)/12=(1-17)/12= -1.333
in exercises 67 and 68, sketch the region of integration and the solid whose volume is given by the double integral. 67. l 3 0 l 2-2x>3 0 a1 - 1 3 x - 1 2 yb dy dx 68. l 4 0 l 216-y2 -216-y2 225 - x2 - y2 dx dy
Answers
In exercise 67, the region of integration is the triangle in the first quadrant that lies above the line y = (2/3)x + 3/2. The solid whose volume is given by the double integral is a pyramid with a triangular base. In exercise 68, the region of integration is the disk in the xy-plane centered at the origin with radius 6. The solid whose volume is given by the double integral is a hemisphere.
In exercise 67, the double integral is taken over the region R in the xy-plane defined by 0 ≤ x ≤ 3 and (2/3)x + 3/2 ≤ y ≤ 2. This region is a triangle in the first quadrant that lies above the line y = (2/3)x + 3/2.
To sketch the solid whose volume is given by the double integral, we consider the integrand f(x,y) = (1/2)(3x - 2y + 3). The double integral ∬R f(x,y) dy dx gives the volume of the solid bounded by the surface z = f(x,y) and the xy-plane over the region R.
We can see that the surface z = f(x,y) is a plane that intersects the xy-plane along the line y = (3/2)x + 3/2, and it intersects the y-axis at (0,3) and the x-axis at (1.5,0). Therefore, the solid whose volume is given by the double integral is a pyramid with a triangular base.
In exercise 68, the double integral is taken over the region R in the xy-plane defined by x^2 + y^2 ≤ 225. This region is a disk in the xy-plane centered at the origin with radius 6.
To sketch the solid whose volume is given by the double integral, we consider the integrand f(x,y) = √(225 - x^2 - y^2). The double integral ∬R f(x,y) dy dx gives the volume of the solid bounded by the surface z = f(x,y) and the xy-plane over the region R.
We can see that the surface z = f(x,y) is a hemisphere with radius 15 centered at the origin. Therefore, the solid whose volume is given by the double integral is a hemisphere.
Visit here to learn more about integration:
brainly.com/question/988162
#SPJ11
What is the range of the function?
The function f(x) = (x - 4)(x - 2) is shown.
10
O all real numbers less than or equal to 3
O all real numbers less than or equal to - 1
O all real numbers greater than or equal to 3
O all real numbers greater than or equal to - 1
Answers
Answer:
The range of the function is all real numbers greater than or equal to -1.
Step-by-step explanation:
Second order polynomials are continous and have an absolute maximum or minimum that restricts the set of the range associated with the function. A fair approach to estimate the range is rewritting the expression into parabola form, which is:
\(y - k = C \cdot (x-h)^{2}\)
Where:
\(C\) - Vertix parameter, dimensionless. If \(C > 0\), then vertix is an absolute minimum, but if \(C < 0\), vertix is an absolute maximum.
\(x\) - Independent variable, dimensionless.
\(y\) - Dependent variable, dimensionless.
\(h\) - Location of the vertix with respect to the independent variable, dimensionless.
\(k\) - Location of the vertix with respect to the dependent variable, dimensionless. This value restrics the set corresponding to the range of the polynomic function.
First, we have to expand polynomial into its standard form:
\(y = (x-4)\cdot (x-2)\)
\(y = x^{2}-6\cdot x +8\)
Now, we are going to complete the square and factorize the resultant expression until parabola form is obtained:
\(y = x^{2}-6\cdot x + 9 -9 + 8\)
\(y = (x-3)^{2} -1\)
\(y + 1 = 1 \cdot (x-3)^{2}\)
Since the vertix parameter is positive, then vertix is an absolute minimum. The location of the vertix with respect ot the depedent variable is \(k = -1\). Therefore, the range of the function is all real numbers greater than or equal to -1.
What is (-m)⁻³n if m = 2 and n = -24?
Answers
Answer:
-3
Step-by-step explanation:
(-2)^-3 x (-24)
(-2)^3 becomes 1/(-2)^3 in order to make the negative exponent a positive one.
then, you do 1/-8 (the -8 is the (-2)^3 simplified) x -24
1/-8 x (24) = 24/-8 = -3.
Hope this helps! :)
Identify the factors of the function y = 6x2 – 9x
Answers
Answer:
3x(2x - 3)
Step-by-step explanation:
Given
y = 6x² - 9x ← factor out 3x from each term
= 3x(2x - 3)
To factor the expression 3x2 – 9x, Caleb found the GCF as shown.
List the factors:
3x2 = 3 • x • x
9x = 3 • 3 • x
GCF = 3 • 3 • x • x = 9x2
What is Caleb’s error?
Answers
Answer:
Caleb’s error was :
instead of selecting the least exponent ,Caleb took the highest exponent.
Step-by-step explanation:
3x² = 3 • x • x
(in this factorization the exponent of 3 is 1 and the exponent of x is 2)
9x = 3 • 3 • x
(in this factorization the exponent of 3 is 2 and the exponent of x is 1)
• The common factors of 3x² and 9x are 3 and x
In order to determine the GCF ,we have to Compare the exponents of the common factors then take the numbers which have the least exponent value.
• in the factorization of 3x² the exponent of 3 is 1
and in the factorization of 9x the exponent of 3 is 2
The least exponent is 1 Then we take it.
• in the factorization of 3x² the exponent of x is 2
and in the factorization of 9x the exponent of x is 1
The least exponent is 1 Then we take it.
Conclusion:
GCF(3x² , 9x) = 3¹ × x¹ = 3x
given f(x) = 10-4x
find f (8)