Answers
Answer:
x=9
Step-by-step explanation:
5x=3x+18
subtract 3x
2x=18
x=9
Answer:
\(15^2+90x\)
Step-by-step explanation:
Related Questions
What is the probability that a random sample of 12 second grade students results in a mean reading rate of more than 95 words per minute?
Answers
The probability that a random sample of 12 second grade students results in a mean reading rate of more than 95 words per minute is 0.4582.
Given that the population mean, \(\mu\) = 90 wpm
The standard deviation of the population ,\(\sigma\) = 10
Sample size, n = 12
Sample mean, \(\bar x\) = 95
The reading rate of students follows the normal distribution.
Let z = \(\frac{\bar x - \mu}{\frac{\sigma}{\sqrt n} }\)
= \(\frac{95 - 90}{\frac{10}{\sqrt 12} }\)
= 1.732
Probability that the mean reading exceeds 95 wpm = P(\(\bar x\) >95)
= P(z>1.732)
= 1- P(z<1.732)
= 0.4582
[The value 0.4582 found from the area under the normal curve using tables].
Learn more about Normal Distribution at https://brainly.com/question/27701525
#SPJ4
Help me please, will mark brainliest

Answers
Answer:
Step-by-step explanation:
Surface area is the sum of the areas of all faces (or surfaces) on a 3D shape. A cuboid has 6 rectangular faces. To find the surface area of a cuboid, add the areas of all 6 faces. We can also label the length (l), width (w), and height (h) of the prism and use the formula, SA=2lw+2lh+2hw, to find the surface area.
The following graph shows a proportional relationship.
What is the constant of proportionality between
�
yy and
�
xx in the graph?

Answers
The constant of proportionality between y and x in the graph is 3
What is the constant of proportionality between y and x in the graph?From the question, we have the following parameters that can be used in our computation:
The graph
On the graph, we have the following readings
(x, y) = (1, 3)
Using the above as a guide, we have the following:
The constant of proportionality between y and x in the graph is
k = y/x
substitute the known values in the above equation, so, we have the following representation
k = 3/1
Evaluate
k = 3
Hence, the constant of proportionality between y and x in the graph is 3
Read more about proportional relationship at
https://brainly.com/question/28651666
#SPJ1
anyone here can someone help me plz plz I will give a Brainiest

Answers
Answer:
Change in Y over change in X. So down 8 and over 2. Simplified it would be 4/1
Find three positive consecutive even integers such that the product of the first and second is 80 more than 15 times the third
Answers
The three consecutive even numbers are 20, 22 and 24.
How to find the even numbers?The three positive consecutive even integers have the first and second is 80 more than 15 times the third.
Even numbers are number that can be divide by two without remainder.
Therefore,
let
x = first number
Hence,
x, x + 2 , x + 4
15(x + 4) + 80 = x(x + 2)
x(x + 2) = 15(x + 4) + 80
x² + 2x = 15x + 60 + 80
x² - 15x + 2x - 140 = 0
x² - 13x - 140
(x - 20)(x + 7)
Hence,
x = 20
Therefore, the numbers are 20, 22 and 24.
learn more on even numbers here: https://brainly.com/question/14286582
#SPJ1
Which of the following is the solution to 113x>> -5?
Answers
Answer:
\(x>-\frac{5}{113}\)
Step-by-step explanation:
\(113x>>-5\\\\\mathrm{Divide\:both\:sides\:by\:}113\\\frac{113x}{113}>\frac{-5}{113}\\\\Simplify\\\\x>-\frac{5}{113}\)
2nd attempt Feedback Whee Periodic Table The radius of an exoplanet is \( 8.00 \) times larger than Earth's radius. What is the ratio of Earth's cooling time to the exoplanet's cooling time?
Answers
The ratio of the cooling time of Earth to the cooling time of the exoplanet is 16,777,216.
What is an exoplanet?An exoplanet, also known as an extrasolar planet, is a planet that orbits a star other than the Sun, which is part of our solar system. An exoplanet is one of many planets that might exist in the universe outside of our solar system.
The ratio of the cooling time of Earth to the cooling time of the exoplanet can be determined using Stefan-Boltzmann's Law and Wien's Law.
We first need to use the Stefan-Boltzmann Law in order to calculate the cooling time.
σT⁴ = L/(16πR²)
σ(5780)⁴ = (3.846 × 10²⁶ W)/(16π(6.3781 × 10⁶)² m²)
Ratio of the exoplanet's radius to the Earth's radius:
re/rE = 8.00
Ratio of the exoplanet's mass to the Earth's mass:
me/mE = (re/re)³ = 8³ = 512 (since density is assumed to be the same for both planets)
Ratio of the exoplanet's luminosity to the Earth's luminosity:
Le/LE = (me/mE)(re/rE)² = 512(8)² = 32768
Ratio of the exoplanet's temperature to the Earth's temperature:
Te/TE = (Le/LE)¹∕⁴ = 32768¹∕⁴ = 32.0
The Wien Law can now be used to determine the ratio of the cooling times of the two planets.
(T/wavelength max)E = 2.898 × 10⁻³ m K(5780 K) = 1.68 × 10⁻⁸ m (using Earth as the comparison planet)
(T/wavelength max)e = 2.898 × 10⁻³ m K(Te)(8.00) = wavelength max (using the exoplanet)
Ratio of the wavelengths:
wavelength max,e/wavelength max,E = (Te/TE)(re/rE) = 32.0 × 8.00 = 256
Ratio of the cooling times:
cooling time,e/cooling time,E = (wavelength max,e/wavelength max,E)³ = 256³ = 16,777,216
Hence, the ratio of Earth's cooling time to the exoplanet's cooling time is 16,777,216.
Learn more about exoplanet here: https://brainly.com/question/28668192
#SPJ11
This afternoon Greta left school, rode the bus 7/12 of a mile, and then walked 1/3 of a mile to get home. How much farther did Greta ride than walk?
Answers
1/3 x 4 = 4/12
7/12 - 4/12 = 3/12
Given the following data, find the age that represents the 48th percentile. ages of presidents 53 61 50 52 67 58 62 45 67 48 43 58 52 52 52
Answers
The age that represents the 48th percentile is 53.
To find the age that represents the 48th percentile given the data below, we first need to arrange the data in ascending order.43, 45, 48, 50, 52, 52, 52, 53, 58, 58, 61, 62, 67, 67Next, we need to determine how many values are in the data set. In this case, there are 14 values. We need to find the rank of the 48th percentile, which is equal to 0.48 * 14 = 6.72, which we can round up to 7 since we can't have a fraction of a rank.The age that represents the 48th percentile is the 7th value in the ordered data set, which is 53. Therefore, the age that represents the 48th percentile is 53.
Learn more about percentile :
https://brainly.com/question/16797504
#SPJ11
9,16,23,...
Find the 46th term?
Answers
The 46th term is 324.
A line is perpendicular to y = -1/5x + 1 and intersects the point negative (-5,1) what is the equation of this perpendicular line?
Answers
Answer: y = 5x + 26
Step-by-step explanation:
To find the equation of a line that is perpendicular to the given line y = -1/5x + 1 and passes through the point (-5, 1), we need to determine the slope of the perpendicular line. The given line has a slope of -1/5. Perpendicular lines have slopes that are negative reciprocals of each other. So, the slope of the perpendicular line will be the negative reciprocal of -1/5, which is 5/1 or simply 5. Now, we have the slope (m = 5) and a point (-5, 1) that the perpendicular line passes through.
We can use the point-slope form of a linear equation to find the equation of the line:
y - y1 = m(x - x1)
Substituting the values, we get:
y - 1 = 5(x - (-5))
Simplifying further:
y - 1 = 5(x + 5)
Expanding the brackets:
y - 1 = 5x + 25
Rearranging the equation to the slope-intercept form (y = mx + b):
y = 5x + 26
Therefore, the equation of the perpendicular line that passes through the point (-5, 1) is y = 5x + 26.
Bob is training for a marathon and varies his workouts from day to day. On Monday, Bob ran at 10 MPH. On Tuesday, he ran at a pace of 15 MPH. By what percent did his running speed increase from Monday to Tuesday?
Answers
Answer:
u know i dont do math!!
jk i am good at %!!!!!!!!
Step-by-step explanation:
Answer is 50%
: )
<3
What is the value of x in the right triangle below?
Show your work and round your answer to the nearest hundredth

Answers
Answer:
9
Step-by-step explanation:
Based on the Pythagorean theorem, A equals the square root of C squared minus B squared. By plugging in these numbers, you get 9.
Calculate the test statistic 2
A local retailer currently schedules employees based on the assumption that they serve customers uniformly throughout the week (the same number each day). Management is starting to question this assumption and decides to collect data on the number of customers served each day of the week to
perform a Chi-Square goodness-of-fit test at a 5% significance level.
Monday Tuesday Wednesday Thursday Friday
Number Served 40 33 35 32 60
Total 200
Provided the assumptions of the test are satisfied, calculate the test statistic 2
Answers
The value of a Chi-Square goodness-of-fit test at a 5% significance level is 13.45
We need to perform a Chi-Square goodness-of-fit test at a 5% significance level.
First we need to calculate the expected count
expected value = ∑(x)/n
= (40 + 33 + 35 + 32 + 60)/5
= 200/5
= 40
Now we need tocalculate the test statistic value
Observed expected O - E (O - E)^t/E %
40 40 0 0 0
33 40 -7 1.225 9.11
35 40 -5 0.625 4.65
32 40 -8 1.6 11.90
60 40 20 10 74.35
Chi square test is 13.45
Therefore, the value of test statistics is 13.45.
To learn more about test staistics refer here
https://brainly.com/question/15980493
#SPJ4
PLEASE HELP ME!!!!!!

Answers
Answer:
a4 = 5/9
Step-by-step explanation:
a1 = 15 , r = 1/3
, a4 =?
Explanation:
To find a4 we use formula
an = a1 · r
n−1
In this example we have a1 = 15 , r = 1/3
, n = 4. After substituting these values to above
formula, we obtain:
an = a1 · r
n−1
a4 = 15 ·
1
3
4−1
a4 = 15 ·
1
27
a4 =
5
9
is this a max or min
y=-(x+3)^2-5
Answers
The quadratic function y = -(x + 3)² - 5 is a maximum
What is the maximum or minimum of a function?The maximum or minimum of a function are the maximum or minimum values of the function.
How to determine if the quadratic function is a maximum or minimum?Since we have the quadratic function y = -(x + 3)² - 5, this is the vertex form of a quadratic polynomial.
The vertex form y = a(x - k) + h with vertex (h, k)
So, we have the vertex of the function at (3, -5).
To determine if there is a maximum or a minimum,it will follow these conditions at the vertex
if d²y/dx² > 0 then it is a minimumif d²y/dx² < 0 then it is a maximumSo, differentiating y twice to get d²y/dx², we have
y = -(x + 3)² - 5
dy/dx = d[-(x + 3)² - 5]/dx
= d[-(x + 3)²]/dx - d5/dx
= -2(x + 3) - 0
= -2x - 6
differentiating again, we get d²y/dx². So,
d(dy/dx)/dx = d(-2x - 6)/dx
d²y/dx² = d(-2x)/dx - d6/dx
= -2 - 0
= -2
Since d²y/dx² = -2 < 0. The quadratic function y = -(x + 3)² - 5 is a maximum
Learn more about maximum of a quadratic function here:
https://brainly.com/question/28769828
#SPJ1
4444444444444444444444
Answers
Answer
5555555555555555555555555555555
Step-by-step explanation:
CAN SOMEONE PLEASE HELP ME !!!!

Answers
Answer:
k = 29
29 + 6 = 35
-3 + 5 = 2
35 + 2 = 37
chipotle can serve one customer every two minutes on average. (a) what is the probability that the wait time for the next customer served will exceed one minute? (b) what is the probability that the wait time for the next customer served you will exceed three minutes, given that they have been waiting for 1 minute already? (c) there are 4 people in line. what is the probability that it will take at most 7 minutes to serve them?
Answers
the probability that it will take at most 7 minutes to serve the 4 customers is approximately 0.9861.
(a) To find the probability that the wait time for the next customer served will exceed one minute, we need to use the exponential distribution with a rate parameter of λ = 0.5 (since the average time between customers is 2 minutes, the rate parameter is 1/2). Let X be the time between customer arrivals. Then, we need to find P(X > 1).
Using the exponential distribution, we have:
\(P(X > 1) = e^(-lamda * 1) = e^(-0.5)\)≈ 0.6065
Therefore, the probability that the wait time for the next customer served will exceed one minute is approximately 0.6065.
(b) Given that the customer has already been waiting for 1 minute, we can model the remaining waiting time as an exponential distribution with a rate parameter of λ = 0.5. Let Y be the remaining time until the next customer is served. Then, we need to find P(Y > 2 | Y > 1).
Using conditional probability, we have:
P(Y > 2 | Y > 1) = P(Y > 2 and Y > 1) / P(Y > 1)
Simplifying the numerator, we have:
P(Y > 2 and Y > 1) = P(Y > 2)
Using the exponential distribution, we have:
\(P(Y > 2) = e^(-λ * 2) = e^(-1)\)
Similarly, we have:
\(P(Y > 1) = e^(-λ * 1) = e^(-0.5)\) ≈ 0.6065
Substituting into the conditional probability formula, we have:
P(Y > 2 | Y > 1) = P(Y > 2) / P(Y > 1) ≈ 0.6065
Therefore, the probability that the wait time for the next customer served will exceed three minutes, given that they have been waiting for 1 minute already, is approximately 0.6065.
(c) Let Z be the total time it takes to serve the 4 customers. Then, Z follows the gamma distribution with shape parameter k = 4 and rate parameter λ = 0.5. We need to find P(Z ≤ 7).
Using the gamma distribution, we have:
P(Z ≤ 7) = F(k, λ, 7)
where F is the cumulative distribution function of the gamma distribution. We can use a calculator or software to find this probability, or we can use the incomplete gamma function as follows:
P(Z ≤ 7) = 1 - Γ(k, λ * 7)
where Γ is the incomplete gamma function. Using a calculator or software, we have:
P(Z ≤ 7) ≈ 0.9861
Therefore, the probability that it will take at most 7 minutes to serve the 4 customers is approximately 0.9861.
Learn more about probability here
https://brainly.com/question/11234923
#SPJ1
describe in words how to calculate the probability of two mece events from their odds using the ratio method.
Answers
To calculate the probability of two separate events using the ratio method, we must first understand the odds associated with each event. The odds are expressed as a ratio, with the first number representing the chances of success and the second number representing the chances of failure. For example, the odds of an event happening might be 3:2, which indicates that there is a 3/5 chance of success.
Once the odds for each event are known, we can calculate the probability of both events occurring by multiplying the odds of each event together. So, for example, if the odds of Event A are 3:2 and the odds of Event B are 4:5, the probability of both events occurring is 3/2 * 4/5 = 6/10. This means that there is a 6 in 10 chance of both events occurring.
To sum up, calculating the probability of two separate events using the ratio method is fairly simple. Just look at the odds associated with each event and multiply them together to get the probability of both events occurring.
For more such questions on Probability.
https://brainly.com/question/30927006#
#SPJ11
x/-9 =3
I dont understand this.
Answers
Answer:
x = -27
Step-by-step explanation:
x / 9 =3
multiply both sides by -9
x = -27
Hope this helps!!
Happy Holidays!!
Final Answer: \(x = -27\)
Steps/Equations:
Question: \(\frac{x}{-9} = 3\)
Step 1: Move the negative sign to the left side.
\(-\frac{x}{9} = 3\)
Step 2: Multiply both sides by \(3\).
\(-x = 3 * 9\)
Step 3: Simplify \(3 * 9\) to \(27\).
\(-x = 27\)
Step 4: Multiply both sides by \(-1\).
\(x = -27\)
~I hope I helped :)~
If csc(0) <0, then in which quadrants could 0 lie? Select all correct answers. Select all that apply: a. Quadrant 1 b. Quadrant II c. Quadrant III d. Quadrant IV
Answers
The value of θ lies in the quadrants III and IV.
Given that;
csc (θ) < 0
Now, if csc(θ) < 0, it means the cosecant of X is negative.
In trigonometry, the cosecant of an angle X is defined as the reciprocal of the sine of X.
So, if csc (θ) < 0,
It implies that the sine of X is negative.
Based on the signs of the trigonometric ratios in each quadrant, we can determine the possible quadrants where X could lie.
The sign of the sine function in each quadrant is as follows:
a. Quadrant 1: sine is positive
b. Quadrant II: sine is positive
c. Quadrant III: sine is negative
d. Quadrant IV: sine is negative
Since we are given that csc(X) < 0 (implying that sine is negative), X could lie in either Quadrant III or Quadrant IV.
Therefore, the correct answer is c. Quadrant III and d. Quadrant IV.
Learn more about trigonometric ratios at:
brainly.com/question/1836193
#SPJ12
The average weight of the three lion cubs at the zoo was 288 pounds. Two of the cubs weighed 261 and 252 pounds. What was the weight of the third cub?
Answers
Answer:
351 pounds
Step-by-step explanation:288 x 3 = 864 pounds
864 - 261 - 252 = 351 pounds
Therefore (261 + 252 + 351)/3 = 288.
So the answer is 351 pounds
inverse proportion- please can someone help me with this question? thanks!

Answers
\(\qquad \qquad \textit{inverse proportional variation} \\\\ \textit{\underline{y} varies inversely with \underline{x}} ~\hspace{6em} \stackrel{\textit{constant of variation}}{y=\cfrac{\stackrel{\downarrow }{k}}{x}~\hfill } \\\\ \textit{\underline{x} varies inversely with }\underline{z^5} ~\hspace{5.5em} \stackrel{\textit{constant of variation}}{x=\cfrac{\stackrel{\downarrow }{k}}{z^5}~\hfill } \\\\[-0.35em] ~\dotfill\)
\(\stackrel{\textit{S varies inversely with }F^2}{S = \cfrac{k}{F^2}}\hspace{5em}\textit{we also know that} \begin{cases} F=8\\ S=125 \end{cases} \\\\\\ 125=\cfrac{k}{8}\implies (125)(8)=k\implies 1000=k~\hfill \boxed{S=\cfrac{1000}{F^2}} \\\\\\ \textit{when F=4, what is "S"?}\qquad S=\cfrac{1000}{4^2}\implies S=\cfrac{125}{2}\)
What would the answer to this question be?
A. 40°
B. 60°
C. 80°
D. 100°

Answers
Answer:
D. 100°
Step-by-step explanation:
A straight line is 180°. Add 50° and 30° (which is 80°) and subtract the total from 180°.
50 + 30 = 80
180 - 80 = 100
Answer:
These angles form a straight line, so they are supplementary angles.
We know that, supplementary angles form 180°.
\(50 + x + 30 = 180 \\ 50 + 30 + x = 180 \\ 80 + x = 180 \\ x = 180 - 80 \\ x = 100\)
=> So, the missing angles is 100°
Write an Equation and solve.10. If tickets to a concert cost $18. How many tickets can you buy with $150?Let x =EquationX=
Answers
Let x = Number of tickets
So, the equation is
\(18x=150\)Solve for x:
\(\begin{gathered} \frac{18x}{18}=\frac{150}{18} \\ x=8.33 \end{gathered}\)Answer: x = 8.33
PLEASE PLEASE PLEASE IM BEGGING U HELP ME ITS DUE SOON THERES 50 QUESTIONS HELP ME NOW PLS
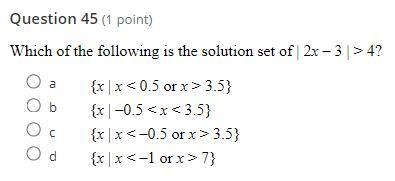
Answers
Answer:
A.{x|x<0.5 or x>3.5}
Step-by-step explanation:
Hope it Helps.15 POINTS!
Please help
Thank you

Answers
Answer: 1. 2 x^3 - 13 x + 15
2. 2 x^4 - 12 x^3 + 13 x^2 + 15 x
Step-by-step explanation:
After an alcoholic beverage is consumed, the concentration of alcohol in the bloodstream (blood alcohol concentration, or BAC) surges as the alcohol is absorbed, followed by a gradual decline as the alcohol is metabolized. The function C(t)=0.135 t e^{-2.802 t}C(t)=0.135te −2.802t models the average BAC, measured in g/dL, of a group of eight male subjects t hours after rapid consumption of 15 mL of ethanol (corresponding to one alcoholic drink) What is the maximum average BAC during the first 3 hours? When does it occur?
Answers
It gradually decreases as alcohol is metabolized. The function C(t)=0.135 t e^{-2.802 t}models the mean BAC measured in g/mL.
The maximum average BAC during 3 hours is 0.0001358 g/mL.
f(t) = α t e−βt --(1)
Let's rewrite this in a simple form:
f(t)= α eˡⁿ ᵗ e⁻βt = αe^(ln t −βt)
Since e^x is strictly increasing and it will be maximized exactly when its argument is maximized, so we can maximize instead:
g(t)=ln t −βt
differentiating with respect to t , and g'(t) = 0
g′(t)=1/t − β = 0
=> t =1/β
we have given a function
C(t)=0.135 t e⁻²·⁸⁰²ᵗ
if we compare it with (1) we get
β = 2.802, 0.135 = α
For it's maximized we need to check the second order condition, and that of g will differentiate again , g′′(t)= −1/t² < 0
We have to compute the derivative of C(t):
C′(t) = 0.135 t⋅(−2.802)e⁻²·⁸⁰²ᵗ + 1.35e⁻²·⁸⁰²ᵗ
For optimum at t₀ if C′(t₀)=0 and C′′(t₀)≠0. Here, we have
C′(t₀) = 0.135t₀⋅(−2.802)e⁻²·⁸⁰²ᵗ₀+ 0.135e⁻²·⁸⁰²ᵗ₀ =e⁻²·⁸⁰²ᵗ₀(−0.135* 2.802t₀+ 0.135)=0
It is clear that e⁻²·⁸⁰²ᵗ₀ not equal to zero for all t₀∈R, so that
=> −0.135* 2.802t₀+0.135=0
=> t₀ = 1/2.802 ≈0.36
let us consider t is in hours, so that it makes t₀ =0.36h≈21.41min. This is the only optimum and one should verify it is indeed a maximum, i.e. C′′(t₀)<0.
Now, easily compute the maximum average BAC, which is C(t₀)=C(0.36) = 0.135 (0.36)e⁻²·⁸⁰²⁽⁰·³⁶⁾
= 0.0486(0.3678) = 0.01787508
Hence, the maximum average BAC, is 0.017 g/dL.
Maximum average BAC during the first 3 hours,
t = 3 , C(t)=C(3) = 0.135 (3)e⁻²·⁸⁰²⁽³⁾ = 0.0001358 g/mL
To learn more about Exponential function, refer:
https://brainly.com/question/12626186
#SPJ4
Use the given information to find the missing side length(s) in each 40° -45° -90° triangle. Rationalize any denominators.
longer leg 1cm
Answers
In the given 40°-45°-90° triangle with a longer leg of 1cm, the shorter leg is √2 cm and the hypotenuse is 2 cm.
To find the missing side length(s) in a 40°-45°-90° triangle, we can use the relationships between the sides. In a 40°-45°-90° triangle, the ratio of the longer leg to the shorter leg is 1:√2, and the ratio of the shorter leg to the hypotenuse is 1:√2.
Given that the longer leg is 1cm, we can use these ratios to find the other side lengths.
To find the shorter leg, we can multiply the longer leg by √2:
Shorter leg = 1cm * √2 = √2 cm
To find the hypotenuse, we can multiply the shorter leg by √2:
Hypotenuse = √2 cm * √2 = 2 cm
So, in the given 40°-45°-90° triangle with a longer leg of 1cm, the shorter leg is √2 cm and the hypotenuse is 2 cm.
To know more about triangle refer here:
https://brainly.com/question/15367648
#SPJ11
