Please help! Correct answer only!
For a fundraiser, there is a raffle with 100 tickets. One ticket will win a $150 prize, and the rest will win nothing. If you have a ticket, what is the expected payoff?
$ ___

Answers
Answer:
Expected Payoff ⇒ $ 1.50 ; Type in 1.50
Step-by-step explanation:
Considering that 1 out of the 100 tickets will have a probability of winning a 150 dollar prize, take a proportionality into account;
\(100 - Number of Tickets,\\1 - Number of Tickets You Can Enter,\\\\1 / 100 - Probability of Winning,\\$ 150 - Money Won,\\\\Proportionality - 1 / 100 = x / 150, where x - " Expected Payoff "\\\\1 / 100 = x / 150,\\100 * x = 150,\\\\Conclusion ; x = 1.5 dollars\)
Thus, Solution ; Expected Payoff ⇒ $ 1.50
Related Questions
The combined area of a square and a rectangle is 33 square meters. The width of the rectangle is 1 meter more than the length of one side of the square and the length of the rectangle is 3 meters more
than its width.
a) Calculate the dimensions of the rectangle and its perimeter
b) Calculate the dimensions of the square.
Answers
Answer:
Step-by-step explanation:
Square is x meters on each side.
Area of square = x²
Width of rectangle = x+1
Length of rectangle = x+4
Area of rectangle = (x+1)(x+4) = x²+5x+4
Combined area = 2x²+5x+4 = 33
2x²+5x-29 = 0
x = [-5+√(5²-4(2)(-29))]/[2(2)] = [-5 +√257]/4
Construct a truth table for each of these compound propositions
a) p → ⇁p
b) p ↔ ⇁p
c) p ⊕ (p V q) d) (p ∧ q) → (p V q) e) (p → ⇁p) ↔ (p ↔ q) f) (p ↔ q) ⊕ (p ↔ ⇁q)
Answers
After considering the given data we conclude that there truth table is possible and is placed in the given figures concerning every sub question.
A truth table is a overview that projects the truth-value of one or more compound propositions for each possible combination of truth-values of the propositions starting up the compound ones.
Every row of the table represents a possible combination of truth-values for the component propositions of the compound, and the count of rows is described by the range of possible combinations.
For instance, if the compound has just two component propositions, it comprises four possibilities and then four rows to the table. The truth-value of the compound is projected on each row comprising the truth functional operator.
To learn more about truth table
https://brainly.com/question/28605215
#SPJ4



Find the X- and y-intercept of the line.
2x + 3y = -18
Answers
Answer: x = -9, y = -6
y = mx + b
2x + 3y = -18
Assuming x = 0
2(0) + 3y = -18
y = -6
Assuming y = 0
2x + 3(0) = -18
x = -9
Answer:
x-intercept = -9
y-intercept = -6
Step-by-step explanation:
The equation is
=> 2x+3y = -18
Finding x-intercept
Let's assume y = 0
The equation becomes
=> 2x = -18
Dividing both sides by 2
=> x = -9
Finding y-intercept:
Let's assume x = 0
The equation becomes
=> 3y = -18
Dividing both sides by 3
=> y = -6
Find the mean of the following set: 30, 16, 29, 14, 21
Answers
Answer:
the mean is 18.2, median is 16, and there is no mode
Step-by-step explanation:
Answer:
22
Step-by-step explanation:
mean is the average of the number.you have to add up all the number then divide it by how many numbers there are.
your question is :30,16,29,14,21 (5 number)
(30+16+29+14+21) / 5 = 22
, evaluate and simplify.

Answers
The difference quotient of the function f(x) = 4x² - 5x is 8x + 4h - 5.
What is the difference quotient of the given function?The formula for difference quotient is expressed as:
\(\frac{f(x+h)-f(x)}{h}\)
Given the function in the question:
f(x) = 4x² - 5x
To solve for the difference quotient, we evaluate the function at x = x+h:
First;
f(x + h) = 4(x + h)² - 5(x + h)
Simplifying, we gt:
f(x + h) = 4x² + 8hx + 4h² - 5x - 5h
f(x + h) = 4h² + 8hx + 4x² - 5h - 5x
Next, plug in the components into the difference quotient formula:
\(\frac{f(x+h)-f(x)}{h}\\\\\frac{(4h^2 + 8hx + 4x^2 - 5h - 5x - (4x^2 - 5x)}{h}\\\\Simplify\\\\\frac{(4h^2 + 8hx + 4x^2 - 5h - 5x - 4x^2 + 5x)}{h}\\\\\frac{(4h^2 + 8hx - 5h)}{h}\\\\\frac{h(4h + 8x - 5)}{h}\\\\8x + 4h -5\)
Therefore, the difference quotient is 8x + 4h - 5.
Learn more about difference quotient here: https://brainly.com/question/6200731
#SPJ1
converir 150g a radiones
Answers
Answer:
?
Step-by-step explanation:
ANSWER QUICK!!
Which of the following is an example of the ASCEND?
A. a bird landing on the ground
B. a hiker climbing a mountain
C. a car traveling through a tunnel
D. a submarine lowering below the surface
Answers
Answer:
answer is B
Step-by-step explanation:
he goes up
Ascend means to go upward and when the hiker climbs a mountain he is climbing upwards
someone please help me.
Answers
Answer:
and i
Step-by-step explanation:
oop.
deepthi has a board that is 6 feet long. she plans to use it to make 4 shelves whose lengths are to be a series of consecutive odd numbers. how long should each shelf be in inches?
Answers
Lengths are:
First shelf = 15 inch
Second shelf = 17 inch
Third shelf = 19 inch
Fourth shelf = 21 inch
Define length.The measurement or size of something from end to end is referred to as its length. To put it another way, it is the greater of the higher two or three dimensions of a geometric shape or object. For instance, the length and width of a rectangle define its dimensions.
Given,
Length of the board = 6 feet
Length of the board = 6(12)
Length of the board = 72 inches
Let the length of first shelf be x inch
Then, length of second shelf be x +2 inches
Length of third shelf is x +4 inch.
Length of fourth shelf be x+ 6 inch.
Total length:
x + x + x +x +2+4+6 = 72
4x = 72 - 12
4x = 60
x = 60/4
x = 15 inch
So,
Lengths are:
First shelf = 15 inch
Second shelf = 17 inch
Third shelf = 19 inch
Fourth shelf = 21 inch
To learn more about to length, visit:
https://brainly.com/question/8552546
#SPJ4
At Cass High School, 2/3 of the students play a sport. Of the students who play a sport, 2/5 play football. What fraction of the students at Cass High School play football? *
Answers
Answer:
4/15
Step-by-step explanation:
2/3 play sports
2/5 play football
Of the 2/3 that play sports, 2/5 of them play football
2/3(2/5) = 4/15
If a person invests $190 at 8% annual interest, find the
approximate value of the investment at the end of 10 years.
Answers
Answer:
$410
Answer From Gauth Math
Step-by-step explanation:
This the problem of compound interest
If any amount P is invested at rate of r% per year then its value after n years is given by
amount =
______________________________
Given
p = $190
r =8%
n = 10 year then

Find the sector area (Show work)

Answers
Answer:
Use MATH.WAY, it will help with any math problem
Step-by-step explanation:
I need some help please

Answers
Answer:
x+2
hope this helps ;)
and cute pfp
Answer:
Step-by-step explanation:
x-1, because 3 fits the criteria, x>=1
abanklends money for a year at an interest rate of 7%, and the inflation rate for that year turns out to be 5%. what is the bank's real rate of return for that year? 2.0% 3.5% 12.0% 6.0%
Answers
The bank's real rate of return for that year is 2.0%.
To calculate the real rate of return, we subtract the inflation rate from the nominal interest rate. In this case, the nominal interest rate is 7% and the inflation rate is 5%.
Real rate of return = Nominal interest rate - Inflation rate
Real rate of return = 7% - 5%
Real rate of return = 2.0%
Therefore, the bank's real rate of return for that year is 2.0%.
The real rate of return represents the actual increase in purchasing power or wealth after adjusting for inflation. It measures the return on an investment after accounting for the effects of inflation.
In this scenario, the bank lends money at an interest rate of 7%. However, the inflation rate for that year is 5%. The inflation rate erodes the purchasing power of money over time. Therefore, to determine the bank's real rate of return, we subtract the inflation rate from the nominal interest rate.
By subtracting 5% (inflation rate) from 7% (nominal interest rate), we get a real rate of return of 2.0%. This indicates that the investment made with the bank has a real return of 2.0% after accounting for the effects of inflation.
It's important to consider the real rate of return when evaluating the profitability or value of an investment. The real rate of return reflects the true growth or decline in purchasing power and provides a more accurate assessment of the investment's performance.
To know more about rate of return refer here:
https://brainly.com/question/17164328?#
#SPJ11
what is the best estimate for this sum?14 27responsesthe sum will be close to 14.the sum will be close to , 1 fourth, .the sum will be close to 12.the sum will be close to , 1 half, .the sum will be close to 1.
Answers
The best estimate for this sum 14 + 27 is the sum will be close to 14.
Estimation is basically rounding off of numbers to the nearest one. ten or hundred place.
The best estimate for this sum
= The sum of 14 + 27 = 41
The difference between 14 and 41 is 27.
The difference between 12 and 41 is 29.
The difference between 1/4 and 41 is greater than 27.
The difference between 1/2 and 41 is also greater than 27.
So best estimate for this sum 14 + 27 will be the sum will be close to 14.
To learn more about estimation refer here
https://brainly.com/question/107547
#SPJ4
Builtrite has calculated the average cash flow to be $14,000 with a standard deviation of $5000. What is the probability of a cash flow being between than $16,000 and $19,000 ? (Assume a normal distribution.) 16.25% 18.13% 23.90% 2120%
Answers
The correct answer is that the probability of a cash flow being between $16,000 and $19,000 is approximately 18.59%.
To calculate the probability of a cash flow being between $16,000 and $19,000, we can use the standard deviation and assume a normal distribution.
We are given that the average cash flow is $14,000 with a standard deviation of $5,000. These values are necessary to calculate the probability.
The probability of a cash flow falling within a certain range can be determined by converting the values to z-scores, which represent the number of standard deviations away from the mean.
First, we calculate the z-score for $16,000 using the formula: z = (x - μ) / σ, where x is the cash flow value, μ is the mean, and σ is the standard deviation. Plugging in the values, we get z1 = (16,000 - 14,000) / 5,000.
z1 = 2,000 / 5,000 = 0.4.
Next, we calculate the z-score for $19,000: z2 = (19,000 - 14,000) / 5,000.
z2 = 5,000 / 5,000 = 1.
Now that we have the z-scores, we can use a standard normal distribution table or calculator to find the corresponding probabilities.
Subtracting the probability corresponding to the lower z-score from the probability corresponding to the higher z-score will give us the probability of the cash flow falling between $16,000 and $19,000.
Looking up the z-scores in a standard normal distribution table or using a calculator, we find the probability for z1 is 0.6554 and the probability for z2 is 0.8413.
Therefore, the probability of the cash flow being between $16,000 and $19,000 is 0.8413 - 0.6554 = 0.1859, which is approximately 18.59%.
So, the correct answer is that the probability of a cash flow being between $16,000 and $19,000 is approximately 18.59%.
To learn more about probability click here:
brainly.com/question/31828911
#SPJ11
The probability of a cash flow between $16,000 and $19,000 is approximately 18.59%.
To calculate the probability of a cash flow being between $16,000 and $19,000, we can use the standard deviation and assume a normal distribution.
We are given that the average cash flow is $14,000 with a standard deviation of $5,000. These values are necessary to calculate the probability.
The probability of a cash flow falling within a certain range can be determined by converting the values to z-scores, which represent the number of standard deviations away from the mean.
First, we calculate the z-score for $16,000 using the formula: z = (x - μ) / σ, where x is the cash flow value, μ is the mean, and σ is the standard deviation. Plugging in the values, we get z1 = (16,000 - 14,000) / 5,000.
z1 = 2,000 / 5,000 = 0.4.
Next, we calculate the z-score for $19,000: z2 = (19,000 - 14,000) / 5,000.
z2 = 5,000 / 5,000 = 1.
Now that we have the z-scores, we can use a standard normal distribution table or calculator to find the corresponding probabilities.
Subtracting the probability corresponding to the lower z-score from the probability corresponding to the higher z-score will give us the probability of the cash flow falling between $16,000 and $19,000.
Looking up the z-scores in a standard normal distribution table or using a calculator, we find the probability for z1 is 0.6554 and the probability for z2 is 0.8413.
Therefore, the probability of the cash flow being between $16,000 and $19,000 is 0.8413 - 0.6554 = 0.1859, which is approximately 18.59%.
So, the correct answer is that the probability of a cash flow being between $16,000 and $19,000 is approximately 18.59%.
To learn more about probability click here:
brainly.com/question/31828911
#SPJ11
The ponderal indexis a measure of the "leanness" of a person. A person who is h inches tall and weighs w pounds has a ponderal index I given by I = a. Compule the ponderal index for a person who is 76 inches tall and weighs 192 pounds: Round to the nearest hundredth. b. What is a man's weight if he is 77 inches tall and has a ponderal index of 11.56 ? Round to the nearest whole number. a. The ponderal index for a person who is 76 inches tall and weighs 192 pounds is (Round to the nearest hundredth as needed.)
Answers
The ponderal index cannot be computed without the value of the constant "a" in the formula. Therefore, the ponderal index for a person who is 76 inches tall and weighs 192 pounds cannot be determined.
To compute the ponderal index, we need the formula and the value of the constant "a."
a) The formula for the ponderal index is given as I = a, where I represents the ponderal index and a is a constant. However, the value of the constant "a" is missing in the provided information. Without knowing the value of "a," we cannot compute the ponderal index for a person who is 76 inches tall and weighs 192 pounds.
b) Similarly, without knowing the value of the constant "a," we cannot determine the weight of a man who is 77 inches tall and has a ponderal index of 11.56.
To compute the ponderal index or determine the weight, we need the specific value of the constant "a" in the given formula.
Learn more about index here :-
https://brainly.com/question/32793068
#SPJ11
14. Simplify the expressions
a. 12 - 5y + 21 + y -23
Answers
Answer:
10 - 4y
Step-by-step explanation:
Combine like terms. 12, 21 and -23 add up to 10, and -5y + y is -4y.
Then, together, we have 10 - 4y (answer)
Answer:
\(\large\boxed{10 - 4y}\)
Step-by-step explanation:
12 - 5y + 21 + y - 23
Combine like terms (add -5y to + y)
12 + 21 - 4y - 23
Add 12 + 21
33 - 4y - 23
Subtract 23 from 33
\(\large\boxed{10 - 4y}\)
This is the simplest form of the expression.
Hope this helps :)
Please help me and others that will stumble on this problem.
Which lists all of the y-intercepts of the continuous function in the table?
(0, 0)
(–1, 0), (2, 0)
(–1, 0), (0, 0)
(–1, 0), (0, 0), (2, 0)

Answers
Answer:
A (0,0)
Step-by-step explanation:
When a function intersects the y-axis then the point of intersection is called y-intercept of the function,
Also, for y-intercept x = 0.
That is, if f(x) is the function then its y-intercept is (0, f(0) )
By the given table for x = 0, f(x) = 0
Hence, the y-intercept of the given function is (0,0),
Option A is correct.
HELP ME PLEASE!!! THIS IS DUE TONIGHT
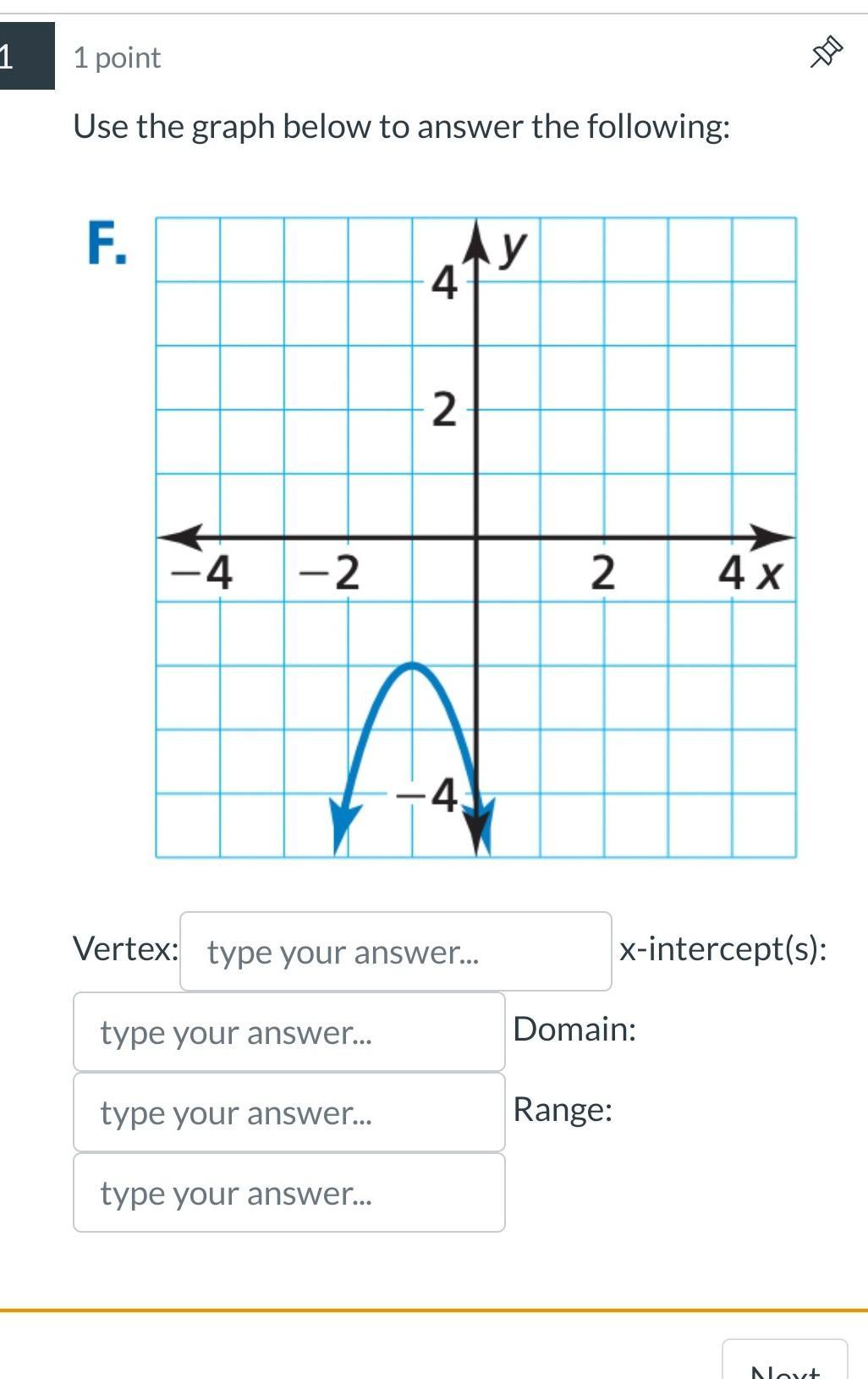
Answers
vertex: (-1,-2)
no x intercepts
domain: negative infinity to positive infinity
range: negative infinity to -2
Bob makes 7% commission on all of the snacks he sells at his snack stand. If he needs to make $3500 a month to pay his bills, how much does he need to sell in snacks every month to pay his bills?
Answers
Find the slope of the line that passes through the points
(3,5) and (5,13) and type the answer below. Start your
answer with m=
Answers
Answer:
m=4
Step-by-step explanation:
Adam's cousin, John, has a utility function given by V(B,W)=3B
2
+W
2
. 'd.1) Are John's preferences monotone? Are they strictly monotone? Justify your answers. (3 marks) 'd.2) Are John's preferences convex? Are they strictly convex? Justify your answers. (3 marks) 'd.3) Do John's preferences satisfy the diminishing marginal rate of substitution property? Explain. (2 marks) (d.4) Assume that the prices are as indicated above (P
B
=5 and P
W
=40), and John's income is I>0. Obtain John's optimal bundle.
Answers
John's preferences are monotone but not strictly monotone. John's preferences are convex but not strictly convex. John's preferences satisfy the diminishing marginal rate of substitution property.
John's preferences are monotone because the utility function V(B,W) is increasing in both B (the quantity of good B) and W (the quantity of good W). However, they are not strictly monotone since the utility function does not strictly increase with each increment of B or W.
John's preferences are convex because the utility function V(B,W) is a strictly convex function. This can be observed from the positive second derivatives of both B and W in the utility function. However, they are not strictly convex since the utility function is not strictly increasing at an increasing rate.
John's preferences satisfy the diminishing marginal rate of substitution (MRS) property. This can be shown by calculating the MRS, which is given by the ratio of the marginal utility of B to the marginal utility of W (∂V/∂B / ∂V/∂W). In this case, the MRS is 6B/W. As the quantities of B and W increase, the MRS decreases, indicating diminishing marginal utility of B relative to W.
To determine John's optimal bundle, we need information about his income (I). With the given prices (P_B = 5 and P_W = 40), we can set up the consumer's optimization problem by maximizing utility subject to the budget constraint (P_B × B + P_W × W = I). By solving this constrained optimization problem, we can find the specific quantities of B and W that maximize John's utility given his income and prices. However, since information about John's income is not provided, we cannot obtain the exact optimal bundle without this information.
Learn more about constrained optimization problem here:
https://brainly.com/question/33436493
#SPJ11
⅝y -6 < 4
plz show work
Answers
Answer:
\(y<16\)
Step-by-step explanation:

Solve the equation x2 + + 7x= 30
O A. x= 15 and x= -2
0 B x=-6 and x = 5
0 C x= -10 and x= 3
O D. x= 10 and x= -3
Answers
Answer:
x^2+7x=30
x^2+7x-30=0
Here a=1,b=7 and c=-30
Now,
Discriminant(D)=b^2-4ac
=7^2-4×1×(-30)
=49+120=169
By applying Quadratic formula
x=-b+- root over b^2-4ac÷2a
=-7+- root over D ÷ 2×1
=-7 +- root over 169 ÷2
=-7 +- 13 ÷2
Now,
Either x=-7+13÷2=6÷2=3
Or x=-7 -13 ÷2=-20÷2=-10
Hence, ans is (C) x=-10 and x=3
A lump of butter has a mass of 250 g and a volume of 290 cm³. Find its density in g/cm³. Give your answer to 3 decimal places.
Answers
The density in butter has a mass of 250g and volume of 290cm³ is 0.862 g/cm³.
What is meant by density?Density is a physical property of matter that is defined as the amount of mass per unit of volume. It is measured in units of kilograms per cubic meter (kg/m^3) and is usually represented by the Greek symbol ρ (rho).
Density is a measure of how tightly the particles of a substance are packed together. The denser a substance is, the more mass it contains in a given volume.
Most commonly, density is used to compare different substances, such as solids, liquids, and gases.
In general, solids are more dense than liquids, and liquids are more dense than gases.
The density of a substance can change based on temperature, pressure, and other factors. For example, water has a greater density at 4°C than at any other temperature, and the density of a gas increases with increasing pressure.
Density is an important factor in many physical and chemical processes, including buoyancy, diffusion, and surface tension.
Density is also used in many calculations, such as calculating the volume of a container or the mass of an object.
Density, p = m/v
Where, m is mass of butter and v is volume of butter.
p = 250/290
p = 0.862 g/cm³
To learn more about density, visit
brainly.com/question/1354972
#SPJ1
What is the denominator of the next term in the geometric sequence?
1/2, 1/6, 1/18, 1/54....
Answers
Answer:
The denominator is 162 in the next term. (1/162)
Step-by-step explanation:
The denominator is the bottom number of the fraction.
In the pattern, the top number (numerator) just stays 1 every time.
But the bottom number (denominator) goes:
2, 6, 18, 54...
The pattern is "times 3"
2 × 3 is 6, which is the next number.
6 × 3 is 18.
18 × 3 is 54.
So to find out what comes next, we can times by 3.
54 × 3 is 162.
So 162 is the next denominator of 1/162, the next term in the geometric sequence.
Answer: 1/162
Step-by-step explanation:
Since you multiply by 3 for each denominator, then that means 54 x 3= 162. so the answer would be 1 /162
Take the first 4 digits of your student number as the first number and the last 3 digits as the second number. Write the matlab code to find the greatest common divisor of these numbers using the Euclidean algorithm.
Answers
The required Matlab code to find the greatest common divisor of a number using the Euclidean algorithm is shown.
To find the greatest common divisor (GCD) of two numbers using the Euclidean algorithm in MATLAB, you can use the following code:
% Replace '12345678' with your actual student number
studentNumber = '12345678';
% Extract the first 4 digits as the first number
firstNumber = str2double(studentNumber(1:4));
% Extract the last 3 digits as the second number
secondNumber = str2double(studentNumber(end-2:end));
% Find the GCD using the Euclidean algorithm
gcdValue = gcd(firstNumber, secondNumber);
% Display the result
disp(['The GCD of ' num2str(firstNumber) ' and ' num2str(secondNumber) ' is ' num2str(gcdValue) '.']);
Make sure to replace '12345678' with your actual student number. The code extracts the first 4 digits as the first number and the last 3 digits as the second number using string indexing. Then, the gcd function in MATLAB is used to calculate the GCD of the two numbers. Finally, the result is displayed using the disp function.
Learn more about Matlab code here:
https://brainly.com/question/30763780
#SPJ4
Suad Alwan, the purchasing agent for Dubai Airlines, has determined that the second plane took 20,000 hours to produce. Using an 80% learning curve and a $35-per-hour labor change, he wants to determine the cost of the four additional planes. Time required for the fourth unit = hours (round your response to the nearest whole number).
Answers
Based on an 80% learning curve and the given information that the second plane took 20,000 hours to produce, the time required for the fourth unit is approximately 10,714 hours.
The learning curve concept suggests that as cumulative production doubles, the time required to produce each unit decreases by a certain percentage. In this case, the learning curve is 80%, meaning that the time required to produce each subsequent unit decreases by 20%.
To determine the time required for the fourth unit, we can use the learning curve formula:
Time for nth unit = Time for the first unit * (n^log(learning curve))
Given that the second plane took 20,000 hours to produce, we can use this information to calculate the time for the fourth unit:
Time for fourth unit = 20,000 * (4^log(0.8))
Evaluating the expression, we find that the time required for the fourth unit is approximately 10,714 hours.
Therefore, according to the 80% learning curve, the fourth unit would require approximately 10,714 hours to produce.
learn more about approximately here
https://brainly.com/question/31695967
#SPJ11
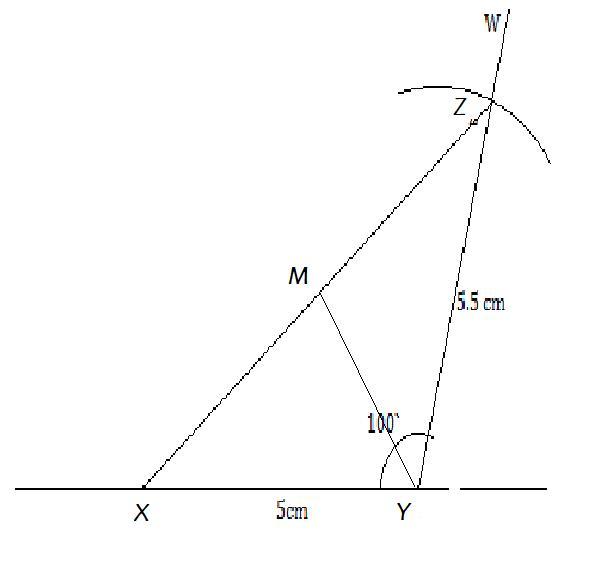
Construct triangle XYZ in which XY= 8.3xm, YZ= 11.9cm. ii, Construct M the midpoint of XZ where angle YXZ= 60. III, Measure YM.
Answers
The length of YM in triangle XYZ, where XY = 8.3 cm and YZ = 11.9 cm, is approximately 2.77 cm.
To construct triangle XYZ with XY = 8.3 cm and YZ = 11.9 cm:
i. Start by drawing a line segment XY with a length of 8.3 cm.
ii. From point X, draw a line segment in the direction of YZ, measuring 11.9 cm. Label the endpoint as Z.
iii. Connect points Y and Z to complete the triangle XYZ.
To construct the midpoint M of XZ with angle YXZ = 60 degrees:
i. Draw a ray from point Y, forming an angle of 60 degrees with line segment YZ. Label the point where the ray intersects XY as M.
ii. Construct a line segment from point M perpendicular to line segment XY. This line segment will intersect line segment XZ at the midpoint M.
The length of YM can be calculated using the Pythagorean theorem.
If we let XZ = a, then XZ/2 = XM = MZ = a/2.
Using the angle YXZ = 60 degrees, we can write the length of YM as:
YM = \(\sqrt{(XM^2 + YX^2)} = \sqrt{((a/2)^2 + (8.3-a)^2)\)
We can solve for a by setting the derivative of YM with respect to a to zero and solving for a, which yields a value of a = 4.85 cm.
Therefore, the length of YM is:
YM = \(\sqrt{((4.85/2)^2 + (8.3-4.85)^2)\) = \(\sqrt{(7.686)\) ≈ 2.77 cm.
For such more questions on Triangle
https://brainly.com/question/17335144
#SPJ11