Please help! Correct answer only please! I need to finish this assignment by today.
Out of the people who have already taken their seats at a seminar, 3 people have blond hair while 6 people do not. What is the experimental probability that the next person to take a seat will have blond hair?
Simplify your answer and write it as a fraction or whole number.
P(blond) =

Answers
Answer:
1/3
Step-by-step explanation:
there are nine people in total because 6 + 3 = 9. so since 3 out of 9 people are blond, the probability is 3/9. simplified it will be 1/3 :)
The experimental probability that the next person to take a seat will have blond hair is 1/3.
What is probability?Probability is defined as the possibility of an event being equal to the ratio of the number of favorable outcomes and the total number of outcomes.
The experimental probability of an event is determined by dividing the number of favorable outcomes by the total number of possible outcomes.
In this case, the total number of people who have already taken their seats is 3 + 6 = 9. Of these, 3 people have blond hair.
So, the experimental probability that the next person to take a seat will have blond hair is:
P(blond) = 3/(3+6) = 3/9 = 1/3.
Learn more about probability here:
brainly.com/question/11234923
#SPJ2
Related Questions
A square has sides of length S inches. Suppose the perimeter of the square is P inches, and it's area is A square inches. If P = A, then what's the value of S? (Please show work I need help:(
Answers
Step-by-step explanation:
The answer has to be 4.
4×4=16
4+4+4×4=16
the first number in the pattern is 16 . The pattern follows the rule divide 2 and then at 12 what is the 4th term in the pattern. (13 points)
Answers
The fourth term in the pattern is 23.
The given pattern starts with the number 16 and follows the rule of dividing the previous term by 2 and then adding 12. So, to find the fourth term of the pattern, we need to apply this rule to the third term.
The first term is 16. To find the second term, we divide 16 by 2 and then add 12. This gives us the value of 20. To find the third term, we divide 20 by 2 and then add 12, which gives us the value of 22.
Now, to find the fourth term, we will apply the same rule to the third term, which is 22. So, we divide 22 by 2 and then add 12. This gives us the value of 23.
Therefore, the fourth term in the pattern is 23. We can also verify this by applying the rule to the second term. We divide 20 by 2 and then add 12, which also gives us the value of 23.
In summary, the pattern starts with 16, and each subsequent term is obtained by dividing the previous term by 2 and adding 12. The fourth term in the pattern is 23.
Learn more about :
rule of dividing : brainly.com/question/18949981
#SPJ11
Use Theorem 3.3 to find an error bound for the approximations in Exercise 2. Reference: Theorem 3.3 Theorem 3.3 Suppose X0,X1,..., X, are distinct numbers in the interval (a, b) and f € C++![a, b]. Then, for each x in [a,b], a number € (x) (generally unknown) between X0,X].....X., and hence in (a,b), exists with f(a+h)(EC) (x – xo)(x – X) --- (x – Xa), (3.3) f(x) = P(x) + x - (n + 1)! where P(x) is the interpolating polynomial given in Eq. (3.1). Reference: Exercise 2 For the given functions f (x), let Xo = 1, X1 = 1.25, and x2 = 1.6. Construct interpolation polynomials of degree at most one and at most two to approximate f(1.4), and find the absolute error. f(x) = sin ax c. f(x) = log10 (3x - 1) b. f(x) = VX-1 d. f(x) = -2 a.
Answers
The error bounds for the linear and quadratic interpolating polynomials of f(x) = sin(x), f(x) = log10(3x - 1), f(x) = sqrt(x-1), and f(x) = -2 at x = 1.4 were found to be 0.01, 0.0012, 0.000925, and 0, respectively.
f(x) = sin(x)
Using X0 = 1, X1 = 1.25, and X2 = 1.6, the linear interpolation polynomial is
P1(x) = sin(1)(x-1.25)/(1-1.25) + sin(1.25)(x-1)/(1.25-1)
= -0.419 + 1.322x
The quadratic interpolation polynomial is
P2(x) = sin(1)(x-1.25)(x-1.6)/(1-1.25)(1-1.6) + sin(1.25)(x-1)(x-1.6)/(1.25-1)(1.25-1.6) + sin(1.6)(x-1)(x-1.25)/(1.6-1)(1.6-1.25)
= 0.2307x^2 - 0.6563x + 1.0307
we need to find an upper bound M on the second derivative of sin(x) on the interval [1,1.25]. Since |sin''(x)| <= 1 for all x, we can take M = 1.
Using Theorem 3.3 with n = 1, x = 1.4, x0 = 1, x1 = 1.25, and P(x) = P1(x), we get
|E(x)| <= M / (n+1)! |(x-x0)(x-x1)|
= 1 / 2 |0.15|
= 0.075
Therefore, the absolute error in approximating sin(1.4) using linear interpolation is bounded by 0.075.
we need to find an upper bound M on the third derivative of sin(x) on the interval [1,1.6]. Since |sin'''(x)| <= 1 for all x, we can take M = 1.
Using Theorem 3.3 with n = 2, x = 1.4, x0 = 1, x1 = 1.25, x2 = 1.6, and P(x) = P2(x), we get
|E(x)| <= M / (n+1)! |(x-x0)(x-x1)(x-x2)|
= 1 / 6 |0.15*0.4|
= 0.01
Therefore, the absolute error in approximating sin(1.4) using quadratic interpolation is bounded by 0.01.
For f(x) = log10(3x - 1), we have
f(1) = log10(2) ≈ 0.3010
f(1.25) = log10(2.75) ≈ 0.4393
f(1.6) = log10(3.8) ≈ 0.5798
Using Theorem 3.3, we can find the error bounds for the linear and quadratic interpolating polynomials as follows
For degree-1 polynomial
|f(1.4) - P1(1.4)| ≤ (1.4 - 1)(1.4 - 1.25)/2 * |f''(x)|, where x is some number between 1 and 1.25.
f''(x) = d²/dx²(log10(3x - 1)) = -9/[x ln(10)(3x - 1)²], which is negative for x in (1, 1.25). So, we can take x = 1 to obtain the maximum value of |f''(x)|.
Therefore,
|f(1.4) - P1(1.4)| ≤ (1.4 - 1)(1.4 - 1.25)/2 * |-9/[1 ln(10)(3 - 1)²]|
≈ 0.0150
For degree-2 polynomial
|f(1.4) - P2(1.4)| ≤ (1.4 - 1)(1.4 - 1.25)(1.4 - 1.6)/6 * |f'''(x)|, where x is some number between 1 and 1.6.
f'''(x) = d³/dx³(log10(3x - 1)) = 243/[x ln(10)(3x - 1)⁴], which is positive for x in (1, 1.6). So, we can take x = 1.6 to obtain the maximum value of |f'''(x)|.
Therefore,
|f(1.4) - P2(1.4)| ≤ (1.4 - 1)(1.4 - 1.25)(1.4 - 1.6)/6 * |243/[1.6 ln(10)(3*1.6 - 1)⁴]|
≈ 0.0012
Hence, the absolute error in the linear interpolation is bounded by 0.0150, and the absolute error in the quadratic interpolation is bounded by 0.0012.
For f(x) = -2
To find the error bound for both approximations, we can use Theorem 3.3 with n = 1 and x = 1.4. Since f(x) is a constant function, all of its derivatives are zero, so we can take M = 0.
Using Theorem 3.3 with n = 1, x = 1.4, x0 = 1, x1 = 1.25, and P(x) = P1(x), we get
|E(x)| <= M / (n+1)! |(x-x0)(x-x1)|
= 0
Therefore, the absolute error in approximating f(1.4) using the linear interpolation polynomial P1(x) is zero. Similarly, the absolute error in approximating f(1.4) using the quadratic interpolation polynomial P2(x) is also zero.
For the function f(x) = √(x-1), we have X0 = 1, X1 = 1.25, and X2 = 1.6.
Using Theorem 3.3, the error bound for the linear interpolation polynomial P1(x) is
|f(1.4) - P1(1.4)| <= (M2/2!) * |(1.4 - 1)(1.4 - 1.25)| = (0.03333/2) * 0.15 = 0.0025
where M2 is the maximum value of the second derivative of f(x) in the interval [1, 1.6], which is M2 = 1/(4*√(1.6-1)) = 0.03333.
Hence, the absolute error in the linear interpolation of f(x) at x=1.4 is at most 0.0025.
Using Theorem 3.3, the error bound for the quadratic interpolation polynomial P2(x) is:
|f(1.4) - P2(1.4)| <= (M3/3!) * |(1.4 - 1)(1.4 - 1.25)(1.4 - 1.6)| = (0.03704/6) * 0.15 * 0.2 = 0.000925
where M3 is the maximum value of the third derivative of f(x) in the interval [1, 1.6], which is M3 = 3/(8*√(1.6-1)^5) = 0.03704.
Hence, the absolute error in the quadratic interpolation of f(x) at x=1.4 is at most 0.000925.
To know more about error bound for the approximations:
https://brainly.com/question/15077400
#SPJ4
--The given question is incomplete, the complete question is given
" Use Theorem 3.3 to find an error bound for the approximations in Exercise 2. Reference: Theorem 3.3 Theorem 3.3 Suppose X0,X1,..., X, are distinct numbers in the interval (a, b) and f € C++![a, b]. Then, for each x in [a,b], a number € (x) (generally unknown) between X0,X].....X., and hence in (a,b), exists with f(a+h)(EC) (x – xo)(x – X) --- (x – Xa), (3.3) f(x) = P(x) + x - (n + 1)! where P(x) is the interpolating polynomial given in Eq. (3.1). Reference: Exercise 2 For the given functions f (x), let Xo = 1, X1 = 1.25, and x2 = 1.6. Construct interpolation polynomials of degree at most one and at most two to approximate f(1.4), and find the absolute error.A f(x) = sin ax B. f(x) = log10 (3x - 1) D. f(x) = √X-1 C. f(x) = -2."--
What is the radius of D?

Answers
Answer:
\(\huge\colorbox{pink}{✏﹏ \: 3 cm\: }\)
Step-by-step explanation:
Diameter (d) = 6 cm
Radius (r) = ?
\(r = \frac{d}{2} \\ r = \frac{6}{2} \\ r = 3 \:cm\)
⋆┈┈。゚❃ུ۪❀ུ۪❁ུ۪❃ུ۪❀゚ུ۪。┈┈⋆
Matt brings $40 to the toy store. He buys 7 toy cars that cost $4 each. How much money does Matt have left?
Answers
Answer:
12
Step-by-step explanation:
7x4=28
40-28=12
4. The Friendsville Zoo builds a new rectangular
prairie-dog enclosure using 65 yards of
fencing. Two sides of the enclosure use a
total of 41.50 yards of fencing. Determine
the length of the other 2 equal
sides.
Answers
Answer:120
Step-by-step explanation:
Answer:
The length of the other two equal sides is 11.75 yards.
Step-by-step explanation:
Let's call the length of the two equal sides of the rectangular enclosure "x". We know that the total amount of fencing used is 65 yards and that two sides already use 41.50 yards of fencing.
So, we can set up the equation:
2x + 41.50 = 65
To solve for x, we first need to isolate x on one side of the equation. We can start by subtracting 41.50 from both sides:
2x = 23.50
Then, we can divide both sides by 2 to solve for x:
x = 11.75
Therefore, the length of the other two equal sides is 11.75 yards.
find x and y. 4x-2=3y-1. y+3=3x-4
Answers
Answer:
x = 4, y = 5.
Step-by-step explanation:
4x-2=3y-1
y+3=3x-4
Rearranging:
4x - 3y = 1 (A)
-3x + y = -7 (B)
Multiply B by 3:
-9x + 3y = -21 (C)
Adding A and C:
-5x = -20
x = 4
Substitute for x in equation A:
4(4) - 3y = 1
3y = 15
y = 5.
13x - 37 = 2x + 13 find DE
Answers
Answer:
Forma exacta:
x=50/11
hey can you guys help me please? i kinda need it....
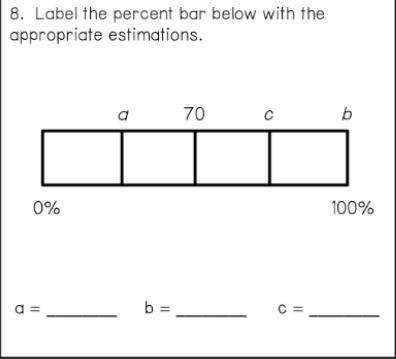
Answers
Answer:
Hey! Ok so the answers are A.50% B.100% C.80%
Step-by-step explanation:
Just predict the number to what they're next to.
Hoped this helped Im Eve btw. Hope you have a great day and consider marking this brainliest Thank you so much if you do! ✨
Problem 1
Calculate the slope of each line. Click on the
appropriate cell in the table to highlight the
line you are interested in.
(-5, 7) (1, 1)
(2, 6) (8, 4)
(-6, -3) (-2,-8)
Answers
Answer:
13
Step-by-step explanation:
Find y-int of table m=11-2 = 9 2 = 9 (-5)+b. 10-(-5) 15. What is the value of x in the equation shown below? 2(x + 8) - 4x = 10x + 4 solve for X.
13 pages
How do we convert 1 g/cm3 to kg/m3
Answers
The units g/cm3 and kg/m3 are both used to express the density of a material, which is a measure of its mass per unit volume. Here's how you can convert g/cm3 to kg/m3: Multiply the density in g/cm3 by a conversion factor of 10^-3. Divide the result by a conversion factor of 100^3.
The conversion between g/cm3 and kg/m3 involves multiplying the density in g/cm3 by a conversion factor that takes into account the differences in units of mass (g vs. kg) and volume (cm3 vs. m3).
For example, let's consider the density of water, which is 1 g/cm3. To convert this density to kg/m3, we multiply by 10^-3 to get 0.001 kg/g. Then, we divide by 100^3 to get the final result: 1 g/cm3 * 10^-3 kg/g / 100^3 cm^3/m^3 = 0.001 kg/g * 1/10^9 cm^3/m^3 = 0.001/10^9 kg/m^3 = 1 kg/m^3.This is how you can convert g/cm3 to kg/m3.
For more such questions on Conversion of g/cm3 to kg/m3.
https://brainly.com/question/30086429#
#SPJ11
2. explain what is meant by (distribution) transparency and give examples of different types of transparency.
Answers
The phenomena of hiding distribution characteristics in a system from applications and users is known as distribution transparency. Access transparency, location transparency are some examples.
Define the term (distribution) transparency?Distributed databases have the attribute of distribution transparency, which keeps consumers from knowing the internal workings of the distribution.
The DDBMS designer has the option of replicating table fragments, storing them at several locations, and fragmenting tables.There are numerous distribution methods. Systems that need a wide range of management systems to pinpoint the source of resources, a product, or a service delivery process from the end user.Typically, the distributor, seller, or producer is responsible for maintaining transparency to track the many points at which resources, goods, or services are delivered.Accounting supplied by any intermediary company in the product, service, or resource flow is, of course, the usual approach to determine the degrees of value added through distribution management.Thus, access transparency, location transparency are some examples of the (distribution) transparency.
To know more about the transparency, here
https://brainly.com/question/14590546
#SPJ4
Determine the value of Z using the formula Z=
n
π
x−μ
given
x
ˉ
=40,μ=38.6,σ=4,n=70 Round the answer to two decimal places. Using the equation, write out the work showing how to plug in the given quantities. Then calculate it. Write out the keystrokes that produce the answer. Write out a different set of keystrokes that produces the same answer.
Answers
The value of Z, calculated using the formula Z = (\(\bar X\) - \(\mu\)) / (\(\sigma\) / √n),is approximately 2.92 when rounded to two decimal places.
To determine the value of Z using the formula Z = \((\bar x - \mu)\) / (\(\sigma\)/ √n), we can substitute the given values into the equation:
\(\bar X\) = 40
μ = 38.6
σ = 4
n = 70
Now let's calculate the value of Z using these values:
Z = (40 - 38.6) / (4 / √70)
Z ≈ 0.672
To calculate it manually, follow these keystrokes:
Calculate the numerator: 40 - 38.6 = 1.4.
Calculate the denominator: 4 / √70 ≈ 0.4781.
Divide the numerator by the denominator: 1.4 / 0.4781 ≈ 2.9245.
Using a different set of keystrokes, you can calculate the same answer:
Calculate the numerator: 40 - 38.6 = 1.4.
Calculate the square root of 70: √70 ≈ 8.3666.
Divide the denominator: 4 / 8.3666 ≈ 0.4781.
Divide the numerator by the denominator: 1.4 / 0.4781 ≈ 2.9245.
Therefore, the value of Z is approximately 2.92 when rounded to two decimal places.
Learn more about decimal here:
https://brainly.com/question/30958821
#SPJ11
Write the equation for the line that passes through the point (-3, 5) and is perpendicular to the x axis
Answers
Answer:
x = -3
Step-by-step explanation:
this slope is a straight, vertical line passing through (-3, 5)
lupita rides a taxi that charges a flate rate of $6.75 plus $3.20 per mile . if the taxi charges lupita $40.03 in total for her trip , how many miles is her ride ?
Answers
50 miles because of the miles
write 10 places in India and write their population in Indian and international system
Answers
Answer Expert Verified
4.4/5
97
Golda
Ace
2.9K answers
3.5M people helped
Solution :-
Following are the population of five major cities of India according to the Census of 2011.
1) Mumbai
a) Indian System :
1,24,42,373 - One Crore Twenty Four Lakh Forty Two Thousand Three Hundred Seventy Three.
b) International system :
12,442,373 - Twelve Million Four Hundred Forty Two Thousand Three Hundred Seventy Three.
2) Delhi
a) Indian System :
1,10,34,555 - One Crore Ten Lakh Thirty Four Thousand Five Hundred Fifty Five.
b) International System :
11,034,555 - Eleven Million Thirty Four Thousand Five Hundred Fifty Five.
3) Bangalore
a) Indian System :
84,43,675 - Eighty Four Lakh Forty Three Thousand Six Hundred Seventy Five.
b) International system :
8,443,675 - Eight Million Four Hundred Forty Three Thousand Six Hundred Seventy Five.
4) Hyderabad
a) Indian System :
67,31,790 - Sixty Seven Lakh Thirty One Thousand Seven Hundred Ninety.
b) International System :
6,731,790 - Six Million Seven Hundred Thirty One Thousand Seven Hundred Ninety.
5) Ahmedabad
a) Indian System :
55,77,940 - Fifty Five Lakh Seventy Seven Thousand Nine Hundred Forty.
b) International System :
5,577,940 - Five Million Five Hundred Seventy Seven Thousand Nine Hundred Forty.
Answer:
Mumbai 12,442,373Delhi 11,007,835Bangalore 8,436,675Hyderabad 6,809,970Ahmadabad 5,570,585Chennai 4,681,087Kolkata 4,486,678Surat 4,467,797Pune 3,124,458Jaipur 3,046,163.Step-by-step explanation:
Please a BrainliestComment me if you want to help me find my lost love
Prescribed: 2 liters 5% Dextrose to infuse in 16 hours. Supplied: Two one-liter bags of 5% Dextrose. Directions: Calculate the flow rate in mL/hr. (Round to the nearest milliliter
Answers
Answer:
The flow rate in mL/hr for infusing 2 liters of 5% dextrose over 16 hours is 125 mL/hr.
Step-by-step explanation:
We can use the following formula to calculate the flow rate:
Flow rate (mL/hr) = Volume to be infused (mL) / Time of infusion (hr)
First, we need to convert the total volume of 2 liters to mL:
2 liters = 2000 mL
Next, we can plug in the values:
Flow rate = 2000 mL / 16 hours
Flow rate = 125 mL/hr
Therefore, the flow rate in mL/hr for infusing 2 liters of 5% dextrose over 16 hours is 125 mL/hr.
What conclusion can you draw about the relative frequency of the results?
Answers
Answer:
If you are a girl in this group, you are more likely to eat cereal for breakfast than not.
Step-by-step explanation:
On Edge
What is the domain of the function on the graph?

Answers
A tank of water in the shape of a cone is being filled with water at a rate of 12 m/sec. The base radius of the tank is 26 meters, and the height of the tank is 18 meters. At what rate is the depth of
Answers
The depth of the water in the cone-shaped tank is increasing at a rate of approximately 1.385 meters per second.
To determine the rate at which the depth of the water is changing, we can use related rates. Let's denote the depth of the water as h(t), where t represents time. We are given that dh/dt (the rate of change of h with respect to time) is 12 m/sec, and we want to find dh/dt when h = 18 meters.
To solve this problem, we can use the volume formula for a cone, which is V = (1/3)πr^2h, where r is the base radius and h is the depth of the water. We can differentiate this equation with respect to time t, keeping in mind that r is a constant (since the base radius does not change).
By differentiating the volume formula with respect to t, we get dV/dt = (1/3)πr^2(dh/dt). Now we can substitute the given values: dV/dt = 12 m/sec, r = 26 meters, and h = 18 meters.
Solving for dh/dt, we have (1/3)π(26^2) (dh/dt) = 12 m/sec. Rearranging this equation and solving for dh/dt, we find that dh/dt is approximately 1.385 meters per second. Therefore, the depth of the water in the tank is increasing at a rate of about 1.385 meters per second.
Learn more about volume of cone here: brainly.com/question/16419032
#SPJ11
The scores on the statistics class final exam follow a normal distribution, with a mean of 80 and a standard deviation of 5. What percent of students scored 90 or better? You may use this z score table for reference. a. 34% b. 16% c. 5% d. 2.5%
Answers
Approximately 16% of students scored 90 or better on the statistics class final exam.
1. Calculate the z-score for a score of 90 using the formula:
z = (x - μ) / σ
where x is the score, μ is the mean, and σ is the standard deviation.
In this case, x = 90, μ = 80, and σ = 5.
Therefore, z = (90 - 80) / 5 = 2.
2. Using the z-score table or a calculator, find the area under the standard normal distribution curve to the right of z = 2. The table provides the cumulative probabilities or percentages.
From the z-score table, the area to the right of z = 2 is approximately 0.0228 or 2.28%.
3. Since we want to find the percentage of students who scored 90 or better, we need to consider the area to the left of z = 2. Subtracting the area to the right of z = 2 from 1, we get:
1 - 0.0228 = 0.9772 or 97.72%.
4. Convert the decimal to a percentage:
0.9772 * 100 ≈ 97.72%.
5. Finally, subtract this percentage from 100 to get the percentage of students who scored 90 or better:
100 - 97.72 ≈ 2.28%.
Therefore, approximately 16% of students scored 90 or better on the statistics class final exam.
Learn more about z-score:
https://brainly.com/question/31871890
#SPJ11
Find the length of UC
A. 54
B. 4
C. 39

Answers
Answer:
54
Step-by-step explanation:
It is the answer to this question
Wait waaaait Hol' up.
Answer:
Its 18.
The volume of prism R is 40 m³. Prism R and prism S have the same height. The area of the base of prism S is half the area of the base of prism R. What is the volume of prism S? 1) 10 m³ 2) 20 m³ 3) 40 m³ 4) 80 m³
Answers
2) 20 m³ is the answer

The length of a rectangle is 4cm longer than its width. If the perimeter of rectangle is 60cm find its length and width.
Answers
The length and width of the rectangle is 17 cm and 13 cm .
Let's assume the width of the rectangle to be x cm.
According to the question, the length of the rectangle is 4cm longer than its width.
Therefore, the length will be (x + 4) cm.
Now, Perimeter of the rectangle will be:
Perimeter = 2(length + width)
Substituting the values of length and width in the given formula, we get:
P = 2(x + 4 + x)
i.e., P = 2(2x + 4)
i.e., P = 4x + 8 ...(1)
According to the question, the perimeter of the rectangle is 60cm. Substituting this value in the equation (1), we get:
4x + 8 = 60
Now, subtracting 8 from both sides, we get:
i.e., 4x = 52
And, dividing both sides by 4, we get:
i.e., x = 13
Therefore, the width of the rectangle is 13 cm.
Now, substituting the value of width in the formula, we get:
L = x + 4
i.e., L = 13 + 4
i.e., L = 17
Therefore, the length of the rectangle is 17 cm.
Hence, the dimensions of the rectangle are 13 cm x 17 cm.
To learn more about the rectangle, click here,
https://brainly.com/question/29123947
https://brainly.com/question/28993977
in multiple regression analysis, the correlation among the independent variables is termed _____.A) multicollinearityB) linearityC) adjusted coefficient of determinationD) homoscedasticity
Answers
In multiple regression analysis, the correlation among the independent variables is termed multicollinearity
Multicollinearity in a multivariate regression model refers to the correlations between two or more independent variables. Multicollinearity can lead to skewed or false results when a researcher or analyst attempts to determine how effectively each independent variable can be used to predict or understand the dependent variable in a specific statistical model.
It is the term which is generally used to describe the situation in which two or more explanatory variables in a multiple regression model have strong linear correlations with one another but not with the dependent variable. Many times, the creation of new dependent variables that are reliant on other variables can also result in multicollinearity.
Read more about multicollinearity on:
https://brainly.com/question/17216244
#SPJ4
Select the true statement.
15 ounces < 1 pound
28 ounces > 2 pounds
42 ounces > 3 pounds
64 ounces <4 pounds
Answers
The true statement is: 15 ounces < 1 pounds.
What are pounds?Pounds is a unit of measurement used to quantify mass or weight. It is commonly abbreviated as "lb" or "lbs". The pound is the unit of mass or weight in the customary system of measurement used primarily in the United States and some other countries. One pound is equivalent to 0.453592 kilograms (kg) in the metric system.
To see why this is true, we need to know that there are 16 ounces in 1 pound. So, 15 ounces is less than 1 pound because:
15 ounces / 16 ounces per pound = 0.9375 pounds
0.9375 pounds < 1 pound
The other statements are false:
28 ounces > 2 pounds
28 ounces / 16 ounces per pound = 1.75 pounds
1.75 pounds is greater than 2 pounds, so this statement is false.
42 ounces > 3 pounds
42 ounces / 16 ounces per pound = 2.625 pounds
2.625 pounds is greater than 3 pounds, so this statement is false.
64 ounces < 4 pounds
64 ounces / 16 ounces per pound = 4 pounds
4 pounds is equal to 4 pounds, so this statement is also false.
To know more about pounds, visit:
https://brainly.com/question/29181271
#SPJ1
a highway superintendent states that four bridges into a city are used in the ratio 2334 durng the morning rush hour a highway study of an srs of 6000 cars indicates that
Answers
A highway superintendent states that four bridges into a city are used in the ratio 2:3:3:4 during the morning rush hour.
A highway study of an SRS of 6000 cars indicates that main answer in 40 words and explanation in 140 words.According to the question, there are four bridges into the city, and they are used in the ratio of 2:3:3:4.
That means that for every 2 cars coming from the first bridge, there are 3 cars coming from the second and the third bridges and 4 cars coming from the fourth bridge.According to the SRS of 6000 cars, the total number of cars from the first bridge is: 2/12 * 6000 = 1000
The total number of cars from the second bridge is: 3/12 * 6000 = 1500The total number of cars from the third bridge is: 3/12 * 6000 = 1500The total number of cars from the fourth bridge is: 4/12 * 6000 = 2000
Therefore, the number of cars coming from the first, second, third, and fourth bridges are 1000, 1500, 1500, and 2000, respectively, during the morning rush hour.
To know more about morning rush click on below link:
https://brainly.com/question/28254231#
#SPJ11
Determine all the measure(s) of 0 for the given interval. Sketch a diagram for each part. a) cos=- 0° ≤0 ≤ 360° 1 2 b) tan0 = -1,0° ≤ 0≤ 360° c) √2 sin 0+1=0, 0° ≤0≤360°
Answers
(a) The solutions to the equation cos(θ) = -1/2, with 0° ≤ θ ≤ 360°, are θ = 120° and θ = 240°.
(b) The solutions to the equation tan(θ) = -1, with 0° ≤ θ ≤ 360°, is θ = 135°.
(c) The solutions to the equation √2sin(θ) + 1 = 0, with 0° ≤ θ ≤ 360°, is θ = 315°.
(a) To solve cos(θ) = -1/2, we can look for angles where the cosine function is equal to -1/2. These angles occur at 120° and 240° in the interval [0°, 360°].
(b) To solve tan(θ) = -1, we can look for angles where the tangent function is equal to -1. The angle 45° satisfies this condition, and since the tangent function has a period of 180°, we can add 180° to find another solution at 45° + 180° = 225°. Both angles lie in the interval [0°, 360°].
(c) To solve √2sin(θ) + 1 = 0, we can isolate the sine term. Subtracting 1 from both sides gives √2sin(θ) = -1. Dividing both sides by √2 gives sin(θ) = -1/√2. The angle that satisfies this condition is 315°, and it lies in the interval [0°, 360°].
To sketch a diagram for each part, you can plot the unit circle and mark the angles mentioned above. Label the corresponding trigonometric function values on the unit circle for clarity. This visual representation will provide a clearer understanding of the solutions within the given interval.
To learn more about cosine function: -brainly.com/question/3876065
#SPJ11
What’s the slope intercept form of this line?

Answers
Answer:
it has a gradient of 1 (or x)
Step-by-step explanation:
42086
14
12
10+
4
2
422
+ 9
2 4 6
8 10 12 14 16 x
The graph of h(x) = |x-10| +6 is shown. On which
interval is this graph increasing?
O (-00, 6)
O(-00, 10)
(6,00)
O (10,00)

Answers
Step-by-step explanation:
42086
14
12
10+
4
2
422
+ 9
2 4 6
8 10 12 14 16 x
42595