Please help! Correct answer only please! I need to finish this assignment by today.
You flip a coin.
What is P(not tails)?
Simplify your answer and write it as a fraction or whole number.

Answers
Answer:
1/2 or 0.5
Step-by-step explanation:
since there are two options, heads and tails, the probability of not flipping tails is 1/2, since the probability of flipping heads is 1/2
Answer:
1/2
Step-by-step explanation:
There are 2 sides of a coin.
Heads or Tails.
That means you have a 1/2 chance of getting tails. This also means you have 1/2 chance of not getting tails, in other words, getting heads.
Related Questions
I need the answer fast please find the tan(b)
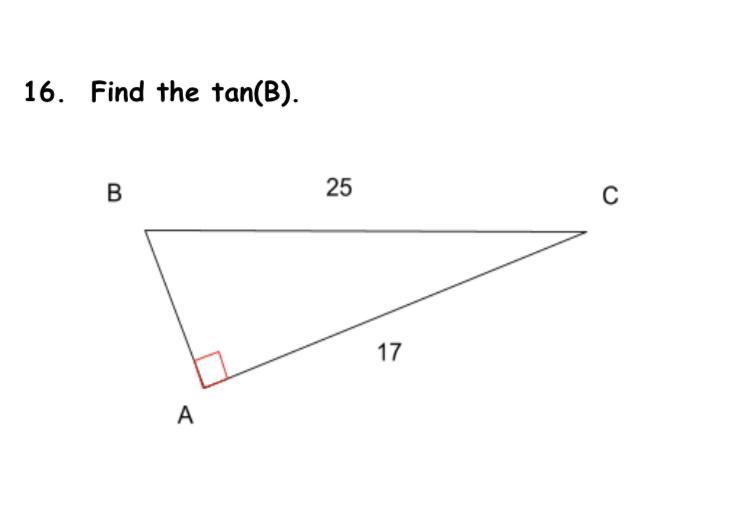
Answers
Answer:
\(\sf \dfrac{17}{25}\)
Step-by-step explanation:
Trigonometry:\(\sf \boxed{\bf Tan \ B=\dfrac{oppoiste \ side \ to \ Tan \ B}{hypotenuse}}\)
\(\sf tan \ B =\dfrac{17}{25}\)
On a scale drawing, the height of a tree is 3.75 inches. If the scale of the drawing is 1 in. : 50 ft, how tall is the tree?
HINT: Write and solve a proportion. You will compare 1 in to 50 feet and then determine how many feet 3.75 inches would be. REMEMBER: When writing your proportion, be sure that whichever (inches or feet) is on top and bottom of one ratio, it is in the same position (top or bottom) on other ratio.

Answers
Amanda and Jasper are hiking along a river bank. They spot a bear feeding along the opposite bank. The angle between Amanda and the bear is , and the angle between Jasper and the bear is . The width of the river is 28 feet.
Answers
The distance between both Amanda and Jasper and the bear is approximately 66.05 feet.
To determine the distance between Amanda and Jasper and the bear, we can use the law of sines, which states that for any triangle ABC with side lengths a, b, and c, and opposite angles A, B, and C, we have:
a/sin(A) = b/sin(B) = c/sin(C)
Let's label the distance between Amanda and the bear as a, the distance between Jasper and the bear as b, and the angle between Amanda and Jasper as C. We can then set up two equations using the law of sines:
a/sin(90 - C) = 28/sin(A)
b/sin(90 - C) = 28/sin(B)
Note that the angles A and B are supplementary, so sin(B) = sin(180 - A) = sin(A).
We can simplify these equations to:
a/cos(C) = 28/sin(A)
b/cos(C) = 28/sin(A)
Dividing the second equation by the first, we get:
b/a = cos(C)/cos(C) = 1
Therefore, a = b, which means that the distances between both Amanda and Jasper and the bear are equal.
To find this distance, we can use the law of cosines, which states that for any triangle ABC with side lengths a, b, and c, and opposite angles A, B, and C, we have:
\(c^2 = a^2 + b^2 - 2ab cos(C)\)
Substituting a = b and C = 180 - A, we get:
\(c^2 = 2a^2 - 2a^2 cos(A)c^2 = 2a^2(1 - cos(A))\)
Taking the square root of both sides, we get:
\(c = a \sqrt{(2 - 2 cos(A))\)
Substituting the given values for A and the width of the river:
A = 42 degrees
width of river = 28 feet
We get:
c = a sqrt(2 - 2 cos(42))
Using a calculator, we find that:
cos(42) ≈ 0.7431
Therefore:
c ≈ a \(\sqrt{(2 - 2 cos(42))\) ≈ 66.05 feet
So, the distance between both Amanda and Jasper and the bear is approximately 66.05 feet.
Learn more about "Distance Using Triangle " :
https://brainly.com/question/26340165
#SPJ11
arrange in ascending order
31/40;78%;0,7
Answers
0.7 = 70%
31/40 = 77.5%
78% = 78%
Hope this is what you were looking for...
what does (5x3)+(4x2) equal
Answers
Answer:
23
Step-by-step explanation:
5 x 3 = 15
4 x 2 = 8
15 + 8
= 23
Here are the probabilities of randomly picking certain letters from a box:
P(A) = 1 5
P(B) = 3 7
P(C) = 1 6
P(D) = 1 7
What is the probability of picking an A, B or C?
Hint: Add the probabilities of the events you want to happen!
Answers
The probabilities of picking an A, a B or a C is given as follows:
167/210.
How to obtain a probability?A probability is obtained by the division of the number of desired outcomes by the number of total outcomes in the context of a problem.
For each event, the probabilities in this problem are given as follows:
P(A) = 1/5.P(B) = 3/7.P(C) = 1/6.P(D) = 1/7.To find the or probability, we add the probabilities of the desired outcomes, hence:
P(A) + P(B) + P(C) = 1/5 + 3/7 + 1/6 = (42 + 90 + 35)/210 = 167/210.
More can be learned about probabilities at https://brainly.com/question/24756209
#SPJ1
Height of the Qutab Minaar is 73 metre. When the last stone on the top of the Qutab Minaar was carried from ground to its top by labour weighting 50 kg (bricks carried weighted 20kg), how much work was done in that job by gravitational force? (g = 10 m/s2)
(d) –12770J
(a) –32110 J
(b) –51100 J
(c) –76990J
Answers
Answer:
peanut butter jelly sandwich
The work done by gravitational force is -51100 J
What is gravitational force?Gravitational force is the force of attraction between all masses in the universe. It is the weakest of all the natural forces. It depends on the mass and distance of the objects.
Given that, a labour has weight 50 kg and bricks carried weighted 20kg to the top of the tower of height 73 m, we need to find the work done by the gravitational force,
W = height × weight × gravity
W = 73 × (50+20) × 10
W = 73 × 70 × 10
W = 51100 J
Hence, the work done by gravitational force is -51100 J
Learn more about gravitational force, click;
https://brainly.com/question/12528243
#SPJ3
Last month you spend $30 on clothing this month you spent 160% of what you spent last minute set up a proportion to model this situation how much did you spend this month
Answers
Answer: See explanation
Step-by-step explanation:
From the question, we are informed that last month $30 was spent on clothing and that this month, 160% of what was spent last month.
The equation to to model this situation will be:
= 160% × $30
= 160/100 × $30
= 1.6 × $30
= $48
That means $48 will be spent this month.
Kieran buys a car for $8000 The following year he sells the car for $7500
Answers
Kieran membeli mobil seharga $8000 Tahun berikutnya dia menjual mobil seharga $7500
Loss :
= $ 8.000 – $7.500
= $ 500
then Loss is $500
#FromIndonesia
3. (07.03 MC)
An equation is shown below:
8(2x14) +13= 4x - 27
What value of x makes the equation true? (4 points)
Answers
Answer:
22222222222222222222222222222
32+b=54 when b = 9
what is the answer
Answers
Step-by-step explanation:
I have two step
step 1
32+b=54
32+9=54
41=54
you divide both side by 41 and the answer is 1 and 1
step two
32+b=54
b=54-32
9=22
you divide both side by 9 and the answer is 2,44
What is an equation of the line that passes through the points (-4, -2) and (-6, -5)?
Answers
Answer:
Step-by-step explanation:
To find the equation of a line that passes through two given points, we can use the point-slope form of the equation of a line. The point-slope form is:
y - y1 = m(x - x1)
where m is the slope of the line, (x1, y1) is a point on the line, and (x, y) are the coordinates of any other point on the line.
To use this formula, we first need to find the slope of the line that passes through the two given points (-4, -2) and (-6, -5). The slope, denoted by m, is given by the formula:
m = (y2 - y1) / (x2 - x1)
where (x1, y1) = (-4, -2) and (x2, y2) = (-6, -5). Substituting these values, we get:
m = (-5 - (-2)) / (-6 - (-4))
= (-5 + 2) / (-6 + 4)
= -3 / -2
= 3/2
So, the slope of the line is 3/2.
Now, we can choose either of the two given points and use it with the slope to write the equation of the line. Let's use the first point, (-4, -2). Substituting the values of x1, y1, and m in the point-slope formula, we get:
y - (-2) = (3/2)(x - (-4))
Simplifying the right side of the equation, we get:
y + 2 = (3/2)(x + 4)
Expanding the right side, we get:
y + 2 = (3/2)x + 6
Subtracting 2 from both sides, we get:
y = (3/2)x + 4
So, the equation of the line that passes through the points (-4, -2) and (-6, -5) is:
y = (3/2)x + 4
31. Lucy gets paid $150 a
week and $10 for every
computer she sells. Write an
expression that represents
her weekly income.
Answers
Answer:
y=10x+150
Step-by-step explanation:
Mr Bosoga received a share of 15 boxes of cremora from a stokvel during December 2022 she has a family of four including herself each family member uses an average of 16g cremora per day which is equivalent to four sachets mr Bosoga claims that all 15 boxes should be enough to last a year of 365days determine the total number of kilograms from 15 boxes
Answers
If 15 boxes of the Cremora received during December 2022, should be enough to last a year for the family of four, the total number of kilograms is 23.36 kg.
How is the total number determined?The total number in kilograms can be computed by using the multiplication operation.
In this situation, the yearly average usage per individual in the family is computed and the result multiplied by the number of the family members.
The number of family members = 4
The average usage of the Cremora = 16 g per day
The average usage of the Cremora per person per 365 days = 5.84 kg (0.016 x 365)
Thus, the total number of kilograms from the 15 boxes of Cremora is 23.36 kg (5.84 kg x 4).
Learn more about the multiplication operation at https://brainly.com/question/20628271
#SPJ1
what is equal to -4(3x+2)=4
Answers
Answer:
x = -1
Step-by-step explanation:
You want the solution to the equation -4(3x+2) = 4.
SolutionFirst of all, we can divide by -4.
3x +2 = -1
Subtracting 2 gives ...
3x = -3
Finally, dividing by 3, we have the solution:
x = -1
<95141404393>
Find the value of (6x + 9)/3 =
Answers
Answer:
2x + 3
Step-by-step explanation:
6x + 9 = 3*2 *x + 3*3 = 3*(2x + 3)
\(\frac{6x+9}{3}=\frac{3*(2x+3)}{3x}=2x + 3\)
Answer:
2x+3
Step-by-step explanation:
(6x+9)/3 6/3=2, 9/3=3
2x+3
what are the dimensions of the largest rectangle that can be formed if all the sides (including the partition) sum to 600 units
Answers
The dimensions of the largest rectangle that can be formed if all the sides (including the partition) sum to 600 units are 150 units x 150 units. This solution yields an area of 22,500 square units.
To find the dimensions of the largest rectangle that can be formed if all the sides (including the partition) sum to 600 units, we can use the concept of optimization. Let's assume that the rectangle has a length of L and a width of W, with a partition dividing it into two smaller rectangles.
Since all the sides (including the partition) sum to 600 units, we can express this mathematically as:
L + W + 2x = 600
where x represents the length of the partition. Rearranging the equation, we get:
L + W = 600 - 2x
The area of a rectangle is given by the formula A = L x W. To find the largest possible area of the rectangle, we need to maximize this function.
Substituting the above equation into the area formula, we get:
A = (600 - 2x - W) x W
Expanding and simplifying, we get:
A = 600W - 2W^2 - Wx
To find the maximum value of A, we can differentiate it with respect to W and set it equal to zero:
dA/dW = 600 - 4W - x = 0
Solving for W, we get:
W = (600 - x)/4
Substituting this value of W back into the equation for A, we get:
A = (600 - x)^2/16
To maximize A, we need to minimize x. Since x represents the length of the partition, this means that the partition should be as small as possible. Therefore, the largest rectangle that can be formed will be a square with sides of 150 units, and the partition will have a length of zero.
To know more about rectangle visit:
https://brainly.com/question/15019502
#SPJ11
finally, what is the total distance the particle travels between time 0 0 and time 16 16 ?
Answers
Without knowing the specific form of the velocity function v(t), it is not possible to determine the exact distance traveled.
Why would we say so?The total distance traveled by a particle can be found by integrating its velocity over time. If the velocity of the particle at time t is given by the function v(t), then the total distance traveled between time t1 and t2 is given by:
distance = ∫v(t)dt from t1 to t2
In this case, we want to find the distance traveled between time 0 and time 16, so t1 = 0 and t2 = 16. Without knowing the specific form of the velocity function v(t), it is not possible to determine the exact distance traveled.
What is velocity?Velocity is a vector quantity that describes the rate at which an object changes its position in space. It is a combination of both speed and direction and is typically represented by the symbol v.
In physics, velocity is defined as the derivative of position with respect to time. If the position of an object at time t is given by the function x(t), then its velocity at time t is given by:
v(t) = dx(t)/dt
This means that velocity is the rate of change of position with respect to time. For example, if an object moves in a straight line from position x1 to x2 in time t, its average velocity during that time is given by:
v = (x2 - x1)/t
Velocity is an important concept in mechanics, as it is used to describe the motion of objects and to calculate various physical quantities, such as force and acceleration.
Learn more about quadratic equations here
https://brainly.com/question/14083225
#SPJ1
Which function has zeros at x = -2 and x = 5?
O f(x) = x2 + 2x - 10
• f(x) = x2 - 2x - 10
O f(x) = X2 + 3x - 10
® f(x) = x2 - 3x - 10
Answers
Answer:
f(x)=x²-3x-10
Step-by-step explanation:
\(f(x) = x {}^{2} - 3x - 10 \\ to \: find \: x \: intercept \:o r \: zero \: substitute \: f(x) = 0\: \\ 0 = x {}^{2} - 3x - 10 \\ x {}^{2} - 3x - 10 = 0 \\ x {}^{2} + 2x - 5x - 10 = 0 \\ x(x + 2) - 5x - 10 = 0 \\ x(x + 2) - 5(x + 2) = 0 \\ (x + 2).(x - 5) = 0 \\ x + 2 = 0 \\ x - 5 = 0 \\ x = - 2 \\ x = 5\)
therefore the zeros of the equation are x₁=-2,x₂=5
1.Find all values of x so that ∣x+2∣<10. 2.Find all values of x so that ∣5x−2∣<0.25.
Answers
1. The solution to the inequality |x + 2| < 10 is -12 < x < 8.
2. There is no solution to the inequality |5x - 2| < 0.25.
1. |x + 2| < 10:
To solve this inequality, we consider two cases:
Case 1: x + 2 ≥ 0
In this case, the inequality simplifies to x + 2 < 10, which gives x < 8.
Case 2: x + 2 < 0
In this case, we need to consider the absolute value of a negative number. |x + 2| is equivalent to -(x + 2), so -(x + 2) < 10. Solving this inequality gives x > -12.
Combining the solutions from both cases, we have -12 < x < 8 as the solution to the inequality |x + 2| < 10.
2. |5x - 2| < 0.25:
To solve this inequality, we consider two cases:
Case 1: 5x - 2 ≥ 0
In this case, the absolute value is not necessary since 5x - 2 is already non-negative. The inequality simplifies to 5x - 2 < 0.25. Solving for x gives x < 0.45.
Case 2: 5x - 2 < 0
In this case, we need to consider the absolute value of a negative number. |5x - 2| is equivalent to -(5x - 2), so -(5x - 2) < 0.25. Solving this inequality gives x > 0.35.
Combining the solutions from both cases, we find that there is no value of x that satisfies the inequality |5x - 2| < 0.25. The absolute value of 5x - 2 cannot be less than 0.25.
In summary, the solution to the inequality |x + 2| < 10 is -12 < x < 8, while there is no solution to the inequality |5x - 2| < 0.25.
To learn more about inequality click here: brainly.com/question/30959203
#SPJ11
Merrill bought m notebooks for $2.50 each and n pens for $1.25 each. Which expression best shows how much she spent?
Answers
Answer:
2.50m+1.25n
Step-by-step explanation:
What is the value of f(x) when x=-3?
f(x) = 2x² +4x+ 10
A: -14
B: -8
C: 16
D: 34
Answers
Answer:
C 16
Step-by-step explanation:
well, you put the given value of x into all the places where the function says "x", and then you calculate.
that's all.
f(-3) = 2(-3)² + 4(-3) + 10 = 2×9 - 12 + 10 = 18 - 12 + 10 = 16
You replace the x’s with -3 in parenthesis
help meeeeeeeeeee!!!

Answers
Answer: 2.9166666666633333333333333333333
Step-by-step explanation:
Answer:
35/12
Step-by-step explanation:
Ok so I’m getting braces in a week and I’m pretty scared about it. But however, does it hurt when they put them in?
Answers
Answer:
Ok so I've had braces and it doesn't really hurt getting put in but it does hurt when they tighten them but you have nothing to worry about :)
Step-by-step explanation:
Answer:
They don't hurt when they put them in however you will feel mild soreness and discomfort as your mouth adjusts to them as with anything, for example, fillings, they feel gritty and uncomfortable at first but your mouth adjusts to it.
" There will be mild soreness or discomfort after the orthodontic wire is engaged into the newly placed brackets, which may last for a few days to a week."
I know its can be scary at first but its for the health of your teeth and not everyone gets that privilege, just make sure to take care of them properly.
Step-by-step explanation:
What is the right translation of these expressions and equations? (with solution)
1. 7 - 2m
2. 3( m + 2) = 15
3. 5m - m(2 - m)
Answers
Answer:
7 - 2m can be translated to "7 minus two times m" or "the difference between 7 and twice m".
3(m + 2) = 15 can be translated to "three times the sum of m and 2 is equal to 15" or "the product of 3 and the sum of m and 2 is 15".
To solve the equation, we can start by distributing the 3 on the left side:
3(m + 2) = 15
3m + 6 = 15
Then, we can subtract 6 from both sides:
3m + 6 - 6 = 15 - 6
3m = 9
Finally, we can divide both sides by 3:
3m/3 = 9/3
m = 3
Therefore, the solution to the equation 3(m + 2) = 15 is m = 3.
5m - m(2 - m) can be translated to "5m minus the product of m and the difference between 2 and m" or "the difference between 5m and m times the quantity 2 minus m".
To simplify the expression, we can use the distributive property to expand the second term:
5m - m(2 - m) = 5m - 2m + m^2 = m^2 + 3m
Therefore, the simplified expression is m^2 + 3m.
An object is placed a distance r in front of a wall, where r exactly equals the radius of curvature of a certain concave mirror. At what distance from the wall should this mirror be placed so that a real image of the object is formed on the wall? Express your answer in terms of r. What is the magnification of the image? Follow the sign conventions. Express your answer using three significant figures.
Answers
The concave mirror should be placed at a distance of 2r from the wall to form a real image of the object on the wall. The magnification of the image is expressed using three significant figures is -0.500.
if the object is placed at a distance r in front of a concave mirror whose radius of curvature is also r, then the image is formed at the same distance r behind the mirror. This is a special case called the "center of curvature" configuration.
To form a real image on the wall, the mirror must be placed such that the object is beyond the mirror's focal point. The focal length of the mirror is half of its radius of curvature, so the focal length is f = r/2.
If the object is placed at a distance x from the mirror, then using the mirror equation:
1/f = 1/do + 1/di
where do is the distance of the object from the mirror and di is the distance of the image from the mirror. In this case, do = x and di = r, so we get:
1/r = 1/x - 1/f
Substituting f = r/2, we get:
1/r = 1/x - 2/r
Solving for x, we get:
x = 2r
Therefore, the mirror should be placed at a distance of 2r from the object to form a real image on the wall.
To find the magnification of the image, we use the magnification equation:
m = -di/do
where m is the magnification, di is the distance of the image from the mirror, and do is the distance of the object from the mirror. In this case, do = x = 2r and di = r, so we get:
m = -r/(2r) = -1/2
Therefore, the magnification of the image is -0.500.
Learn more about concave mirrors at
brainly.com/question/31379461
#SPJ4
Let A be the set of all statement forms in the three variables p, q, and r, and let R be the relation defined on A as follows.
For all S and T in A, S R T ⇔ S and T have the same truth table.
Prove that R is an equivalence relation. Show that it satisfies all the properties you selected in part (a), and submit your proof as a free response.
Answers
In relation to equivalence, it should be reflexive, symmetric, and transitive.
In Maths, a binary relation R across a set X is reflexive if each element of set X is related or linked to itself. In terms of relations, this can be defined as (a, a) ∈ R ∀ a ∈ X or as I ⊆ R where I is the identity relation on A. Thus, it has a reflexive property and is said to hold reflexivity. Symmetric relation is defined In set theory as a binary relation R on X if and only if an element a is related to b, then b is also related to a for every a, b in X. A relation R on a set X is transitive if, for all elements a, b, c in X, whenever R relates a to b and b to c, then R also relates a to c. Each partial order as well as each equivalence relation needs to be transitive.
To learn more about sets and relations,
https://brainly.com/question/13088885
#SPJ4
Find the perimeter of the square shown below:
Area = 49 cm2 plz!! It’s due in 5 minutes!!!!!!!
Answers
Answer:
28 cm
Step-by-step explanation:
If the shape is a square, all the sides are equal. To find the area you multiply the length by the width. Since the area is 49 centimeters, find the square root of 49 to find the length of the length and the height of the square, which is 7. To find perimeter, you add the lengths of all the sides of the square. 7+7+7+7=28.
i do not understand this and you’re trying to find x
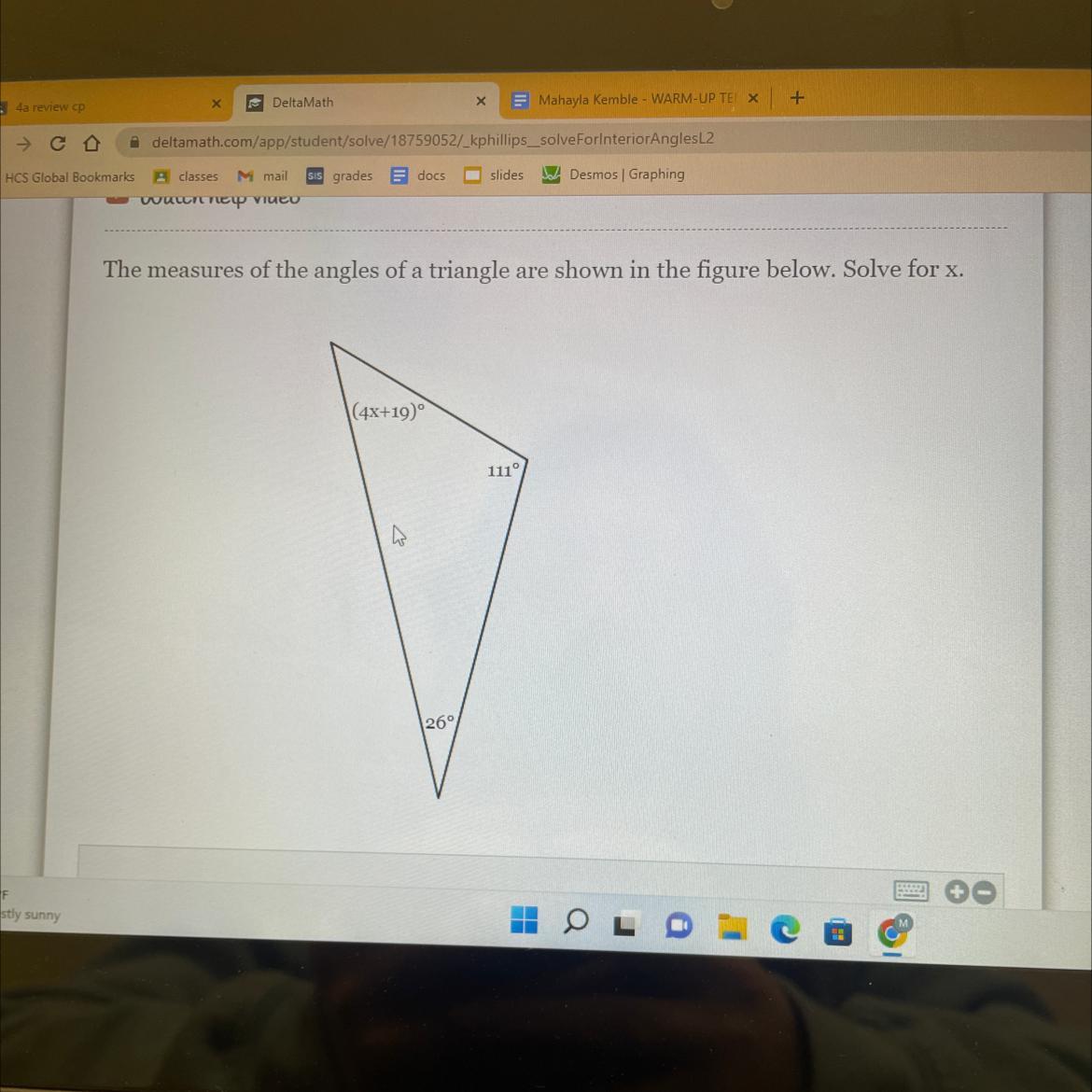
Answers
Answer:
i think it is 56.1868
Step-by-step explanation:
Answer: 6
Step-by-step explanation: all interior angles in a triangle add up to 180.
4x+19+111+26=180
3
Antonio's Pizza Shop charges
$12 for a large cheese pizza
plus $0.50 for each topping added.
Write an equation Antonio can use
to be able to determine the total (y)
for any large pizza no matter the
number of toppings ordered (x).
Answers
Answer:
C = 12 + 1.5t
Step-by-step explanation:
Answer:
$12 + x = y
Step-by-step explanation:
x = number of topping
y = total cost of pizza
Hope this helps :)