Answers
Answer:
A. 14.4 B. 9.24 C. 38.85 D. 175.57 E.430 F.2.60952381
Step-by-step explanation:
a. 3.6 x 4 = 14.4
b. 4.2 x 2.2 = 9.24
c. 11.1 x 3.5 = 38.85
d. 47.5 x 3.7 = 175.57
e. 4.3/0.01 = 430
f. 27.4/10.5 = 2.60952381
Related Questions
What is the area of the circle?

Answers
PLEASE HELP!! The first answer WITH STEPS gets BRAINLY!
Mr. Lehman is a piano tuner. He charges his clients a fixed amount for a house call plus his labor which is based on an hourly rate. The graph below shows how much Mr. Lehman charges as a function of the time required to tune a piano
Which of the following best represents Mr. Lehmans hourly rate for labor?
A. 10$
B. 15$
C. 20$
D. 25$

Answers
=Mr.Lehmans hourly rate for labor is 20$
=30+40=70-50=20
Answer:
The Answer is 15$
You'd need to get the slope
it tells us how he charges with respect to Time
So picking any Point on the graph. Let's say (0,10) and (2,40)
m(slope) = y2-y1/x2-x1
= 40-10/2-0
=30/2
= 15$
Picking other points would still give this value
Solve the given differential equation x^3 y"' - 6y = 0 y(x) = ______ , x > 0
Answers
The solution to the given differential equation is:
\(\[y(x)\ =\ a_0 + a_1x + \frac{1}{4}a_1x^4 + \sum_{n=2}^{\infty} \frac{2a_{n-2}}{(n-2)(n-1)}x^{n+3}\]\)
How did we get the value?To solve the given differential equation
\(x^3y'''\ -\ 6y\ =\ 0,\)
we can use the method of power series. Let's assume a power series solution of the form
\(y(x)\ =\ \sum_{n=0}^{\infty} a_nx^n.\)
Differentiating y(x) with respect to x gives:
\(\[y'(x)\ =\ \sum_{n=0}^{\infty} n a_n x^{n-1}\ =\ \sum_{n=0}^{\infty} (n+1) a_{n+1} x^n\]\)
Differentiating again gives:
\(\[y''(x)\ =\ \sum_{n=0}^{\infty} (n+1)na_{n+1}x^{n-1}\ =\ \sum_{n=0}^{\infty} (n+2)(n+1)a_{n+2}x^n\]\)
Differentiating one more time gives:
\(\[y'''(x)\ =\ \sum_{n=0}^{\infty} (n+2)(n+1)na_{n+2}x^{n-1}\ =\ \sum_{n=0}^{\infty} (n+3)(n+2)(n+1)a_{n+3}x^n\]\)
Substituting these expressions into the differential equation, we have:
\(\[x^3 \sum_{n=0}^{\infty} (n+3)(n+2)(n+1)a_{n+3}x^n - 6 \sum_{n=0}^{\infty} a_n x^n\ =\ 0\]\)
Rearranging the terms and combining like powers of x, we get:
\(\[\sum_{n=0}^{\infty} (n+3)(n+2)(n+1)a_{n+3}x^{n+3} - 6 \sum_{n=0}^{\infty} a_n x^n\ =\ 0\]\)
Now, let's equate the coefficients of like powers of x to zero:
For n=0:
\(\[(3)(2)(1)a_3 - 6a_0 = 0 \implies 6a_3 - 6a_0 = 0 \implies a_3 = a_0\]\)
For n=1:
\(\[(4)(3)(2)a_4 - 6a_1 = 0 \implies 24a_4 - 6a_1 = 0 \implies a_4 = \frac{1}{4}a_1\]\)
\(For \: n\geq 2:
\[(n+3)(n+2)(n+1)a_{n+3} - 6a_n = 0 \implies a_{n+3} = \frac{6a_n}{(n+3)(n+2)(n+1)}\]
\)
Now we can write the solution as:
\(\[y(x)\ =\ a_0 + a_1x + \frac{1}{4}a_1x^4 + \sum_{n=2}^{\infty} \frac{6a_{n-2}}{n(n-1)(n-2)}x^{n+3}\]
\)
Simplifying the series, we get:
\(\[y(x)\ =\ a_0 + a_1x + \frac{1}{4}a_
1x^4 + \sum_{n=2}^{\infty} \frac{2a_{n-2}}{(n-2)(n-1)}x^{n+3}\]
\)
Therefore, the solution to the given differential equation is:
\(\[y(x)\ =\ a_0 + a_1x + \frac{1}{4}a_1x^4 + \sum_{n=2}^{\infty} \frac{2a_{n-2}}{(n-2)(n-1)}x^{n+3}\]\)
where a₀ and a₁ are arbitrary constants to be determined based on the initial conditions or boundary conditions given in the problem.
learn more about differential equation: https://brainly.com/question/1164377
#SPJ1
a population of values has a normal distribution with and . you intend to draw a random sample of size . find the probability that a single randomly selected value is less than 221.3.
Answers
The probability that a single randomly selected value from a normal distribution with mean \($\mu$\) and standard deviation \($\sigma$\) is less than 221.3 is given by \($P(X < 221.3) = \Phi(\frac{221.3-\mu}{\sigma})$\), where \($\Phi$\) is the cumulative distribution function.
The probability that a single randomly selected value from a normal distribution with mean and standard deviation is less than 221.3 is given by \($P(X < 221.3) = \Phi(\frac{221.3-\mu}{\sigma})$\), where the cumulative distribution function. This probability is calculated using the Z-Score formula, which is used to determine the position of a given value in a normal distribution relative to the mean. In this case, the Z-Score is calculated by subtracting the mean from the value 221.3 and dividing the result by the standard deviation. The result is then used to find the probability of a value being lower than 221.3 by looking up the corresponding value in a Z-Table. This is an important concept in statistics as it allows us to determine the probability of a randomly selected value from a normal distribution being less than a given value.
Learn more about probability here
https://brainly.com/question/11234923
#SPJ4
PLEASE HELP ME DUE IN 5 MINS! Evaluate the expression for =10
(−10)(+2)

Answers
Answer:
12
Step-by-step explanation:
(10-10)(10+2)
=12
do whats inside the brackets then multiply (BEDMAS)
hope this helps
Brian buys a computer for £2100.
It depreciates at a rate of 1% per year.
How much will it be worth in 6 years?
Give your answer to the nearest penny where appropriate.
Answers
Answer:
it will be 1974
Step-by-step explanation:
2100*6/100
=126
Answer:
1997.08 pounds at the beginning of 6 years.
Step-by-step explanation:
If you start at 2100 pounds, and it depreciates by .01 every year, you would start by doing this. It wouldn't just be subtracting 21 each year because the value depreciates and 1% would come off the new depreciated value each year.
1st year - 2100*.01 = 21
2100-21 = 2079
2nd year - 2079*.01 = 20.79
2079 - 20.79 = 2058.21
3rd year - 2058.21*.01 = 20.58
2058.21-20.58 = 2037.63
4th year - 2037.63*.01 = 20.38
2037.63-20.38 = 2017.25
5th year - 2017.25*.01 = 20.17
2017.25 - 20.17 = 1997.08
6th year - at the beginning of the 6th year, it would be worth 1997.08.
At the end of the 6th year, it would be: 1997.08*.01 = 19.97. 1997.08-19.97 = 1977.11
I NEED HELP ON THIS ASAP!!

Answers
The perimeter of ΔXYZ is approximately 23.54 units.
How to determine the perimeter?
To determine the perimeter of the triangle ΔXYZ, we need to find the length of all three sides and add them together. We can use the distance formula to find the length of each side:
Side XY:
d(XY) = √[(x₂ - x₁)² + (y₂ - y₁)²]
d(XY) = √[(10 - 2)² + (9 - 5)²]
d(XY) = √(64 + 16)
d(XY) = √80
d(XY) ≈ 8.94
Side YZ:
d(YZ) = √[(x₂ - x₁)² + (y₂ - y₁)²]
d(YZ) = √[(6 - 10)² + (1 - 9)²]
d(YZ) = √(16 + 64)
d(YZ) = √80
d(YZ) ≈ 8.94
Side XZ:
d(XZ) = √[(x₂ - x₁)² + (y₂ - y₁)²]
d(XZ) = √[(6 - 2)² + (1 - 5)²]
d(XZ) = √(16 + 16)
d(XZ) = √32
d(XZ) ≈ 5.66
To find the perimeter, we add up the three side lengths:
Perimeter = d(XY) + d(YZ) + d(XZ)
Perimeter ≈ 8.94 + 8.94 + 5.66
Perimeter ≈ 23.54
Therefore, the perimeter of ΔXYZ is approximately 23.54 units.
To determine the height of this triangle, we can use various methods such as the area formula, Pythagorean theorem, or the distance formula. However, the process of determining the height will be the same as in previous activities, regardless of the triangle's vertices' coordinates.
To know more about coordinates visit :-
https://brainly.com/question/17206319
#SPJ1
Evaluate 13 - 0.75w+8x when w=12 and x= 1 over 2
Answers
Answer:
8
Step-by-step explanation:
Given:
13 - 0.75w + 8x
where,
w = 12
x = 1/2
13 - 0.75w + 8x
Substitute the value of w and x into the equation
= 13 - 0.75(12) + 8(1/2)
= 13 - 9 + 8/2
= 13 - 9 + 4
= 8
Therefore,
13 - 0.75w + 8x = 8
Johnson's Farm charges a fee of $26 to enter their orchard, then charges $6 for every pound of cherries you pick. Mood's Farm does not charge customers an entry fee, but cherries picked cost $8 a pound. How many pounds of cherries would you need to pick in order to pay the same amount at each farm?
Answers
There are 11/3 pounds of cherries at Johnson's Farm in order to pay the same amount as picking 6 pounds of cherries at Mood's Farm.
In general, the unitary method is a useful tool for solving problems like this where we need to compare the cost of two different scenarios. We can set up equations based on the rates or costs involved, and then use algebra to solve for the unknown variables.
To begin, let's use a unitary method to find the total cost of picking cherries at Johnson's Farm. We know the entry fee is $26, so we can start with that. Then, for each pound of cherries picked, the cost is $6. So, if we let x be the number of pounds of cherries picked, the total cost at Johnson's Farm would be:
Total Cost = $26 + $6x
Now, let's use a unitary method to find the total cost of picking cherries at Mood's Farm. We know that there is no entry fee, so we can start with just the per-pound cost of $8. If we let y be the number of pounds of cherries picked, the total cost at Mood's Farm would be:
Total Cost = $8y
To find how many pounds of cherries you would need to pick at each farm in order to pay the same amount, we need to set these two total costs equal to each other and solve for x:
$26 + $6x = $8y
$6x = $8y - $26
x = (8/6)y - 13/3
x = (4/3)y - 13/3
So, if you picked 6 pounds of cherries at Mood's Farm (y = 6), the equivalent cost at Johnson's Farm would be:
x = (4/3)(6) - 13/3
x = 8 - 13/3
x = 11/3
To know more about unitary method here.
https://brainly.com/question/28276953
#SPJ4
Solve for w-39=4w+7(w-3)Simplify your answer as much as possible
Answers
Given the equation:
-39 = 4w + 7(w-3)
Let's solve the equation for w.
To solve take the following steps.
• Step 1.
Apply distributive property
\(\begin{gathered} -39=4w+7(w)+7(-3) \\ \\ -39=4w+7w-21 \end{gathered}\)• Step 2.
Combine like terms
\(-39=11w-21\)• Step 3.
Add 21 to both sides
\(\begin{gathered} -39+21=11w-21+21 \\ \\ -18=11w \end{gathered}\)Step 4.
Divide both sides by 11
\(\begin{gathered} \frac{-18}{11}=\frac{11w}{11} \\ \\ -1.63=w \\ \\ w=-1.63 \end{gathered}\)ANSWER:
w = -1.63
A researcher wants to set up a regression equation where Y is a function X. Evaluate the researcher’s options given the following scenarios: (3)
i. Y is I(0); X is I(0)
ii. Y is I(2); X is I(0)
iii. Y is I(1); X is I(1); and the error term is I(0).
Answers
The appropriate regression model depends on the stationarity properties of both the dependent and independent variables, as well as the error term. The researcher can use a standard OLS regression model with first-order differencing of both Y and X.
In the first scenario, both Y and X are I(0), which means they are stationary time series. In this case, the researcher can perform a standard linear regression analysis, as the stationary series would lead to a stable long-run relationship. The answer from this model will be reliable and less likely to suffer from spurious regressions. In the second scenario, Y is I(2) and X is I(0). This implies that Y is integrated of order 2 and X is stationary. In this case, the researcher should first difference Y twice to make it stationary before performing a regression analysis. However, this approach might not be ideal as the integration orders differ, which can lead to biased results.
In the third scenario, Y and X are both I(1) and the error term is I(0). This indicates that both Y and X are non-stationary time series, but their combination might be stationary. The researcher should employ a co-integration analysis, such as the Engle-Granger method or Johansen test, to identify if there is a stable long-run relationship between Y and X. If co-integration is found, then an error correction model can be used for more accurate predictions.
To know more about regression visit:-
https://brainly.com/question/28168620
#SPJ11
What is the equation of a line through (-4, -5) and a slope of 0? *
Answers
Answer:
y=x-1
Step-by-step explanation:
Answer:
y+5=O
Step-by-step explanation:
Given,
The line passing through the point (-4,-5).
slope=0
Now,
Using properties,
y-y1=m(x-x1)
y-(-5)=0(x-(-4))
y+5=O
the voltage produced by the colorimeter is __________ to the absorbance of the sample and ____________ to the light intensity.
Answers
The colorimeter detects the voltage created when sunlight penetrates the specimen, so the voltage created is exactly proportional to the absorbance of the sample.
What is voltage?When charged electrons (current) are forced through a conducting loop by the weight of an electrical raceway power source, they can perform tasks like lighting a lamp. In a nutshell, voltage equals pressure and is expressed in volts (V).
Here,
The voltage generated by the uv spectrophotometer is inversely proportionate to the amount of light present and linearly proportional to the sample's absorbance.
This indicates that as the sample's absorbance rises, so does the energy the colorimeter generates.
Similar to this, the voltage generated by the colorimeter rises as light strength falls.
The Beer-Lambert Law, which says that a sample's absorbance is directly proportional to its concentration of the absorbing substance and its path length and inversely proportional to incident light intensity, describes this connection.
The colorimeter detects the voltage created when sunlight penetrates the specimen, so the voltage created is exactly proportional to the absorbance of the sample.
To know more about voltage , visit:
https://brainly.com/question/26446532
#SPJ4
Write the constraint described by each of the following statements. Variable terms should all be on the left side of the constraint followed by the correct inequality or equality symbol and the right side should be a numeric value. I recommend using the equation writer in Word under the Insert tab. To receive full credit the constraint should be written with variables on the left hand side and a single numeric value on the right hand side (e.g. 4x1-3x2≤0)
The total production of A and B must at least 100 units.
The quantity of Y must be at least two times as large as one-fifth the quantity of Z.
The ratio of x1 to x2 can be no more than the ratio of 13 to 23.
The quantity of M must be at least one-fourth as large as the sum of P and Q.
The production of D must be no more than 6 more than twice the production of C.
Answers
1) The total production of A and B must be at least 100 units: A + B ≥ 100.
2) Y ≥ 2/5 * Z. 3) x1 / x2 ≤ 13/23. 4) M ≥ 1/4 * (P + Q). 5) D ≤ 2C + 6.
1) The total production of A and B must be at least 100 units:
A + B ≥ 100.
2) The quantity of Y must be at least two times as large as one-fifth the quantity of Z:
Y ≥ 2/5 * Z.
3) The ratio of x1 to x2 can be no more than the ratio of 13 to 23:
x1 / x2 ≤ 13/23.
4) The quantity of M must be at least one-fourth as large as the sum of P and Q:
M ≥ 1/4 * (P + Q).
5) The production of D must be no more than 6 more than twice the production of C:
D ≤ 2C + 6.
In summary:
1) A + B ≥ 100.
2) Y ≥ 2/5 * Z.
3) x1 / x2 ≤ 13/23.
4) M ≥ 1/4 * (P + Q).
5) D ≤ 2C + 6.
Learn more about ratio here:
https://brainly.com/question/13419413
#SPJ11
Find m<1. Please help thank you!

Answers
M<1 = 50°
Have a good night
PLEASE HELP ME Solve the following equation.
-3=z +4
A z=1
B z=-1
C z=-7
D z= 7
Answers
Answer:
Z = -7
Step-by-step explanation:
Answer:
C z = -7
Step-by-step explanation:
(given) -3 = z + 4
(subtract 4 from both sides) -7 = z
(answer) z = -7, so c
(edit: ty for Brainliest *evil laughter*)
Please help. I keep getting these wrong and I am not sure why!
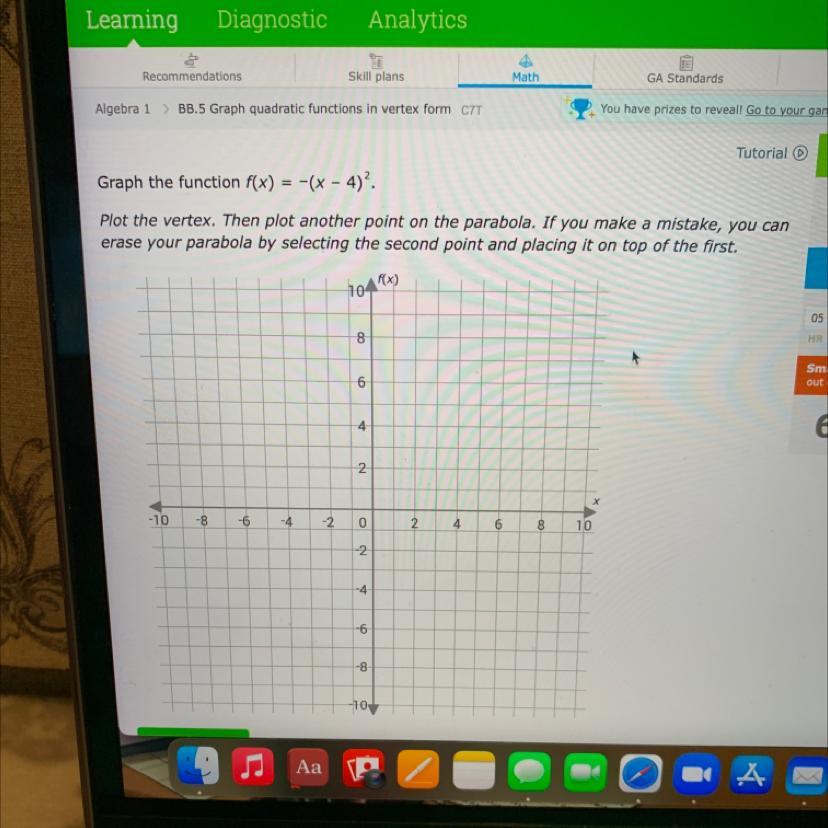
Answers
Solution
\(f\left(x\right)=-\left(x-4\right)^{2}\)The graph
The vertex of a parabola is the point at the intersection of the parabola and its line of
symmetry
Any other point is a point on the graph, you can choose any desired point on the graph


(Annulty number of periods) Youve just bought a new flas-screen TV for $3,400 and the stoce you booght it from offers to let you finance the entire purchase at an annual rate of 16 percent compounded monthly. If you take the fnancing and make monthy payments of $140, how long will is take fo poy off the loan? How much will you pay in interest over the Ifo of the loan? a. The number of years it will take to pay of the loan is years. (Round to one decimal place)
Answers
you will pay approximately $11,542 in interest over the life of the loan.
it will take approximately 82.3 months to pay off the loan.
To calculate the number of years, we divide the number of months by 12:
Years ≈ 82.3 / 12 ≈ 6.9 (rounded to one decimal place)
FV = P * [(1 + r)^n - 1] / r
Where:
FV = Future value of the annuity (total amount paid)
P = Monthly payment amount ($140)
r = Monthly interest rate (16% / 12 = 0.16 / 12 = 0.0133)
n = Number of periods (months)
We need to solve for n. Rearranging the formula, we have:
n = log((FV * r) / (P * r + P)) / log(1 + r)
Plugging in the given values:
FV = $3,400
P = $140
r = 0.0133
n = log(($3,400 * 0.0133) / ($140 * 0.0133 + $140)) / log(1 + 0.0133)
Calculating this expression:
n ≈ log(45.22) / log(1.0133)
Using a calculator, we find:
n ≈ 82.3
To calculate the number of years, we divide the number of months by 12:
Years ≈ 82.3 / 12 ≈ 6.9 (rounded to one decimal place)
So, it will take approximately 6.9 years to pay off the loan.
To calculate the total interest paid, we subtract the initial loan amount from the total amount paid:
Total interest = (P * n) - $3,400
Total interest = ($140 * 82.3) - $3,400
Total interest ≈ $11,542
learn more about value here:
https://brainly.com/question/30145972
#SPJ11
The sum of 10 consecutive integersstarting with 11, equals the sum of 5 consecutive integers, starting with
(A) 22
(B) 29
(C) 31
(D) 33
Answers
Answer: \(\large\boxed{29}\)
Step-by-step explanation:
The sum of 10 consecutive integersstarting with 11
= 11 + 12 + 13 + 14 + 15 + 16 + 17 + 18 + 19 + 20 = 155
Lets try 29:
29 + 30 + 31 + 32 + 33 = 155
Therefore our answer is:
\(\large\boxed{29}\)
Write an inequality to represent the following sentence:
“Six is at least four more than a number.”
Answers
Answer:6 < 4+n
Step-by-step explanation:at least symbol is < . and more than means add .
Can someone please help me with these pleaseeeee

Answers
Please help me!! If you get a fraction please simplify!

Answers
Missing term from each line for the equation are 23u , 0,0.
What is an equation?
An equation is a formula that uses the equals sign to connect two expressions to show that they are equal.
Main Body:
10u +16+ 13u=16
Doing simple addition of like terms , we get:
23u+16=16
Therefore answer for the first part is 23u.
Now subtracting 16 from both side.
23u =0
Therefore 0 is the answer for 2nd part.
Dividing both sides by 23 .
u=0
hence the answer is 0.
The answer for all the parts are 23u , 0, 0.
to learn more about equation cliCk on the below link.
https://brainly.com/question/2972832
#SPJ13
Which functions are positive for the angle of 210 degrees (Select all that apply)
A sin(210)
B cos(210)
C tan(210)
D cot(210)
Answers
\(210^{\circ}~ \text{lies in the third quadrant,}~\text{where}~ \tan \theta ~\text{and}~ \cot \theta ~\text{are positive.} \\\\ \text{Hence the answers are C and D.}\)
PLEASE HELP,!! HURRY!!!!! 40 points!!!
which word best describes the degree of overlap between the two data sets?
Low
None
Moderate
High

Answers
Answer:
moderate since the lines are similar
7. If BD = 7x-10, BC = 4x - 29, and CD = 5x - 9. find each value.
= 7x-10
B
.
D
C
x =
BC =
CD
BD =
If RRC
Answers
Step-by-step explanation:
given,
BD = 7x - 10
BC = 4x - 29
CD = 5x - 9
a/q
BC + CD = BD
so, after inserting the values we got,
4x - 29 + x - 9 = 7x - 10
→ 5x - 38 = 7x - 10
→ 5x - 7x = - 10 + 38
→ 2x = 28
→ x = 28/2 = 14
→ x = 14
therefore value of x is 14
according to the obtained value,
BD = 7x - 10 → 7(14) - 10 = 98 - 10 = 88
BC = 4x - 29 → 4(14) - 29 → 56 - 29 = 27
CD = 5x - 9 → 5(14) - 9 → 70 - 9 = 61
hope this answer helps you dear....take care and may u have a great day ahead!
verifying,
BC + CD = BD
→ 61 + 27 = 88
→ L.H.S = 61 + 27 = 88
so,
LHS = RHS
One teacher wants to give each student 4/9 of a slice of pizza. if the teacher has 4 slices of pizza, then how many students will she be able to hand out pizza to?
Answers
4y - 9 = 3 what is y
Answers
add 9 to both sides
4y = 12
divide both sides by 4 so 4 divided by 4 is one and 12 divided by 4 is 3 thus getting your answer of 3
y=3
how do I find the Domain and Range for:f(x)=(x-2)^2 -2
Answers
Domain: the set of all possible x values of the function.
Since there are no radicals and denominators, the domain of the function is all the real numbers.
Domain= all real numbers
Range = the set of all possible y values of the function
Range= (-2; ∞)
Graph of the function:

Can you factor the problem 36x2+49?
Why or why not?
Answers
Answer:
Yes
Step-by-step explanation:
I dont know why
(A)Find the length of the arc.
(B)Find the area of the sector.
r = 8 cm, Theta = 45°
Answers
a. The length of the arc is 6.28cm
b. The area of the sector is 25.12cm²
What are arc and sector?The arc of a circle is defined as the part or segment of the circumference of a circle. A sector is the space bounded by the arc and the radii of the circle. The smaller area is known as the minor sector and the bigger area is known as the major sector.
The length of an arc = tetha /360 ×2πr
= 45/360 × 2×3.14× 8
= 2×3.142 = 6.28cm
The area of a sector = tetha / 360 × πr²
= 45/360 × 3.14 × 8× 8
= 3.14× 8
= 25.12 cm²
Therefore, the length of the arc is 6.28cm and the area of the sector is 25.12cm²
learn more about arc and sector from
https://brainly.com/question/27116303
#SPJ1
