PLEASE ANSWER QUICKLY
What is the equation in slope-intercept form of the line that passes through the points (9, 4) and
(-9,6)?
Answers
Answer: y = 2/-18 + 5
Related Questions
your brother has $200 saved for a vacation. His airplane ticket is $637. Write and solve an inequality to find out how much he can spend on everything else.
Answers
Let x be the amount your brother can spend. Subtracting the cost of the plane ticket from savings, we have:
x <= 2000 - 637
x <= 1,363
Select the lesser of the two given numbers.
-5, -11
Which is the lesser of the two numbers?
Answers
She must determine height of the clock tower using a 1.5 m transit instrument (calculations are done 1.5 m above level ground) from a distance 100 m from the tower she found the angle of elevation to be 19 degrees. How high is the clock tower from 1 decimal place?
Answers
Step-by-step explanation:
We can use trigonometry to solve this problem. Let's draw a diagram:
```
A - observer (1.5 m above ground)
B - base of the clock tower
C - top of the clock tower
D - intersection of AB and the horizontal ground
E - point on the ground directly below C
C
|
|
|
|
| x
|
|
|
-------------
|
|
|
|
|
|
|
|
|
B
|
|
|
|
|
|
|
|
|
|
|
A
```
We want to find the height of the clock tower, which is CE. We have the angle of elevation ACD, which is 19 degrees, and the distance AB, which is 100 m. We can use tangent to find CE:
tan(ACD) = CE / AB
tan(19) = CE / 100
CE = 100 * tan(19)
CE ≈ 34.5 m (rounded to 1 decimal place)
Therefore, the height of the clock tower is approximately 34.5 m.
Joanne earns $150 per week plus a 5% commission on her sales. If she made $355 last week, what were her sales for this week?
Answers
Answer:
150 + (.05x) = 355
.05x = 205
x = $4100
Step-by-step explanation:
Subtract to find amount of commission made:
355 - 150 = 205
She made $205 in commissions
Divide the amount she made in commission by the percentage she gets:
205 / 0.05 = 4,100
Her sales was $4,100
use method of definite integration to find area of circle :x² + y² = 9
Answers
The area of the circle defined by the equation x² + y² = 9 is 9π square units.
To find the area of the circle using definite integration, we can express the equation x² + y² = 9 in terms of either x or y and then integrate over the appropriate range. In this case, it's more convenient to express the equation in terms of y.
1: Solve the equation for y:
y² = 9 - x²
y = ±√(9 - x²)
2: Determine the limits of integration. Since the equation represents a circle, we need to find the x-values that correspond to the boundaries of the circle.
It is clear that the circle is centered at the origin (0,0) and has a radius of 3. Thus, the limits of integration for x will be -3 to 3.
3: Set up the integral for the area:
A = 2∫[-3 to 3] √(9 - x²) dx
(Note the factor of 2 accounts for both the upper and lower halves of the circle.)
4: Evaluate the integral:
A = 2∫[-3 to 3] √(9 - x²) dx
= 2[1/2 (x√(9 - x²) + 9arcsin(x/3))] [-3 to 3]
= [x√(9 - x²) + 9arcsin(x/3)] [-3 to 3]
= [(3√(9 - 9) + 9arcsin(3/3)) - (-3√(9 - 9) - 9arcsin(-3/3))]
= [(0 + 9arcsin(1)) - (0 - 9arcsin(-1))]
= 18arcsin(1)
= 18(π/2)
= 9π
x² + y² = 9 is 9π square units.
For more such questions on circle, click on:
https://brainly.com/question/28162977
#SPJ8
A spinner 5 equal selection labeled 1- 5 is spun 50 times what is the theoretical probability of spinning an even number
Answers
Answer: 6/25
Step-by-step explanation: Hope this helps
let the random variables and have the joint pmf find the means and , the variances and , the covariance , and the correlation coefficient . are and independent or dependent?
Answers
To find the means, variances, covariance, and correlation coefficient of random variables X and Y with a joint PMF:
- Calculate the means: E[X] and E[Y].
- Compute the variances: Var(X) and Var(Y).
- Find the covariance: Cov(X, Y).
- Determine the correlation coefficient: ρ(X, Y).
Based on the covariance, we can determine if X and Y are independent or dependent.
Let the random variables X and Y have a joint probability mass function (PMF). We need to find the means (expected values), variances, covariance, and correlation coefficient of X and Y, and determine whether they are independent or dependent.
The mean of a random variable X is denoted by E[X] or μX, and it is calculated as the sum of all possible values of X weighted by their respective probabilities. Similarly, the variance of X, denoted by Var(X) or σ²X, measures the spread or dispersion of the values of X around its mean.
The covariance between two random variables X and Y, denoted by Cov(X, Y), measures the degree to which they vary together. It is calculated as the sum of the products of the differences of the values of X and its mean, and the differences of the values of Y and its mean, weighted by their joint probabilities.
The correlation coefficient between X and Y, denoted by ρ(X, Y), quantifies the strength and direction of the linear relationship between them. It is calculated by dividing the covariance of X and Y by the product of their standard deviations.
To determine the means and variances, we can use the following formulas:
E[X] = ∑x∑y x * P(X = x, Y = y)
E[Y] = ∑x∑y y * P(X = x, Y = y)
Var(X) = E[X²] - (E[X])²
Var(Y) = E[Y²] - (E[Y])²
To calculate the covariance, we use the formula:
Cov(X, Y) = E[XY] - E[X]E[Y]
Once we have the means and variances, we can calculate the correlation coefficient using the formula:
ρ(X, Y) = Cov(X, Y) / (√Var(X) * √Var(Y))
Based on the calculations of means, variances, covariance, and correlation coefficient, we can determine whether X and Y are independent or dependent. If the covariance is zero (Cov(X, Y) = 0), then X and Y are independent. Otherwise, they are dependent.
In summary, to find the means, variances, covariance, and correlation coefficient of X and Y, we use the formulas mentioned above. Based on the calculated values, we can determine whether X and Y are independent or dependent.
To know more about joint probability mass function, refer here:
https://brainly.com/question/32066487#
#SPJ11
The square of a number is added to 6
Answers
help me for brainlist.

Answers
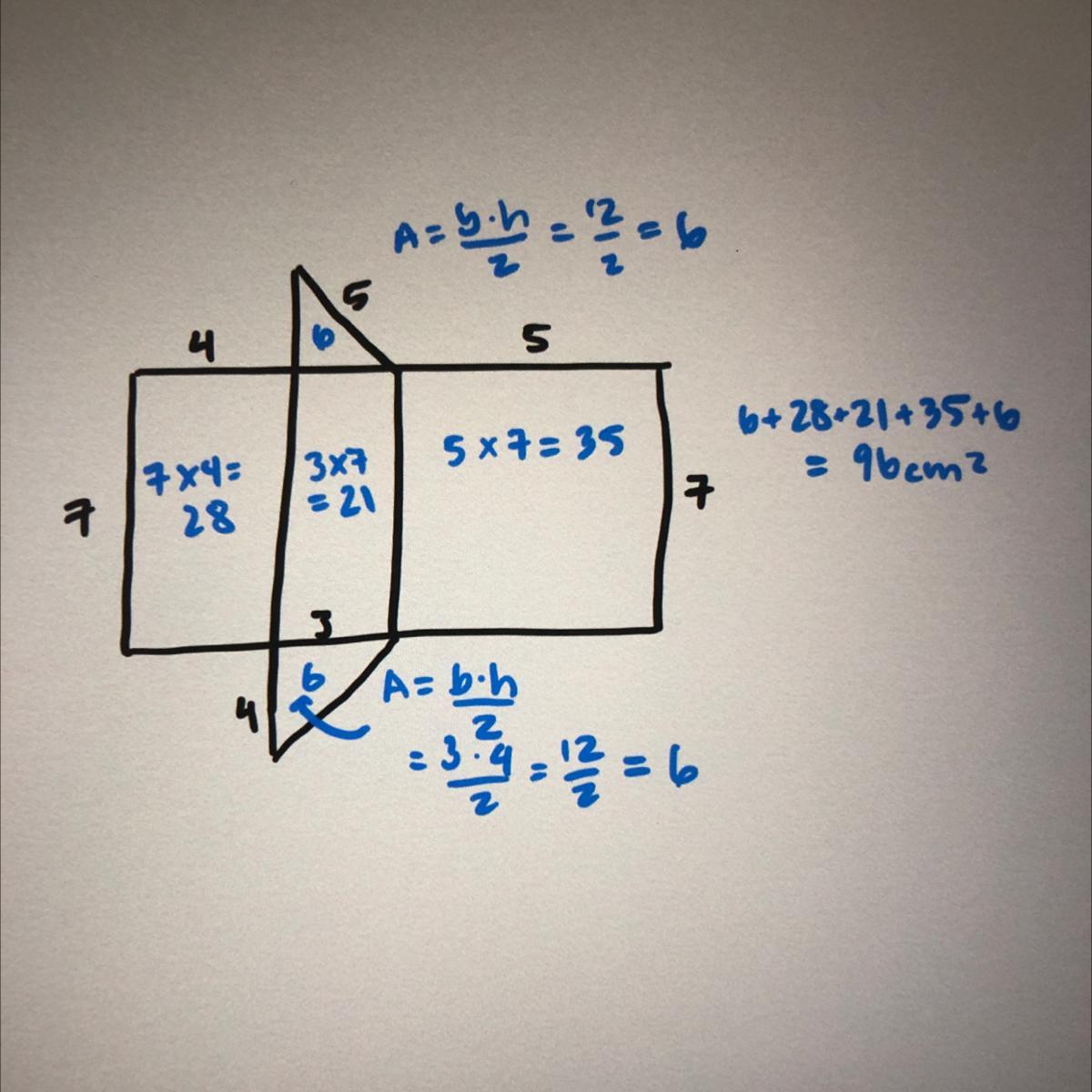
find the area of each rectangle and triangle
add them to get 96
A track has the dimensions shown.
36.5 m
ISTAN
SAMANT
men komm
84.4 m
Ta
inside of track
outside of track
. The track has 8 lanes
• Each lane is 2.1 meters wide
36.5 m
O
TI
16. To the nearest tenth of a meter, what is
the perimeter of the outside of the
track?
Byp
*REQUIRED
ANA
1
√x
Sign out

Answers
Answer:
Step-by-step explanation:
Last year, Karen spent 1.3 months in London, 3.2 months in Prague, and 2.6 months in Ankara. How many months did she spend abroad in total?
Answers
Answer:
she spent approximately 7.3 months abroad in total
Step-by-step explanation:
1.3+3.2+2.6= 7.3
calculate the sum of the series [infinity] an n = 1 whose partial sums are given. sn = 4 − 2(0.6)n
Answers
The sum of the series with partial sums given by Sn = 4 - 2(0.6)ⁿ is 4.
The eries is given as [infinity] an n = 1, and we know the partial sums sn = 4 − 2(0.6)n. To calculate the sum of the series, we can use the formula:
∑an = limn→∞ sn
This means that we take the limit as n approaches infinity of the partial sums sn.
So, plugging in our given partial sums:
∑an = limn→∞ (4 − 2(0.6)n)
Now, as n approaches infinity, the term 2(0.6)n approaches 0 (since 0.6 is less than 1), so the limit simplifies to:
∑an = limn→∞ 4 = 4
Therefore, the sum of the series is 4.
To calculate the sum of the series with partial sums given by Sn = 4 - 2(0.6)ⁿ, you'll need to find the limit of Sn as n approaches infinity.
The series is represented as:
Sum = lim (n→∞) (4 - 2(0.6)ⁿ)
Step 1: Identify the term that goes to zero as n approaches infinity.
In this case, the term is (0.6)ⁿ, as any number between 0 and 1 raised to the power of infinity approaches zero.
Step 2: Calculate the limit.
As n approaches infinity, the term (0.6)ⁿ will approach zero. Therefore, the limit can be expressed as:
Sum = 4 - 2(0)
Step 3: Simplify the expression.
Sum = 4 - 0
Sum = 4
So, the sum of the series with partial sums given by Sn = 4 - 2(0.6)ⁿ is 4.
To know more about series visit-
https://brainly.com/question/26263191
#SPJ11
Please answer it now in two minutes

Answers
Answer:
m∠C = 90°
Step-by-step explanation:
Triangle BDC is a right triangle with the measure of angle D = 90°
By applying Cosine rule in the given triangle,
Since, Cosine of any angle in a right triangle is a ratio of Its adjacent side and Hypotenuse (Opposite side of the right angle)
CosC = \(\frac{\text{Adjacent side}}{\text{Hypotenuse}}\)
CosC = \(\frac{\text{DC}}{\text{BC}}\)
CosC = \(\frac{7}{8}\)
\(C=\text{Cos}^{-1}(\frac{7}{8})\)
C = 28.955
C = 29°
Therefore, m∠C = 29° will be the answer.
Find the surface area
of the figure below:
HELP ASAP!!! PLZZZ

Answers
Answer:
320 cm squared
Step-by-step explanation:
A=2(wl+hl+hw)
2 × (12 × 4 +7 × 4+ 7 × 12)
Have a good day :)
Your friend leaves your house. She later calls you on her cell phone, saying that she's been driving at 60 miles an hour directly away from you the whole time and is now 60 miles away. How long has she been gone?
Answers
Answer: 1hr
Step-by-step explanation: Distance = speed × time
Time = Distance / Speed = 60/60
PLEASE HELP ME =(((((((((((((((((((((((

Answers
Answer:
The answer is
\(y = - 5x - 2\)
Step-by-step explanation:
❃Incase you forgot what the linear equation formula is ☟
\(y = mx + b\)
❃Incase you also forgot, The is what the slope formula is ☟
\(m = \frac{y_2 - y_1 }{x_2 - x_1}\)
➊ First: We are going to be solving for the slope.
\(m = \frac{ - 2 - 3}{0 - ( - 1)} = \frac{ - 5}{ \: \: \: 1} = - 5\)
➋Second: We find the y-intercept.
\(y = mx + b \\ 3 = - 5( - 1) + b \\ 3 = 5 + b \\ \frac{ - 5 = - 5 \ \ \: \: \: \: \: \: }{ - 2 = b}\)
➌Third: Plug in.
\(y = - 5x - 2\)
please help have a lot of math to do today

Answers
Answer:
115 in.^2
Step-by-step explanation:
The total surface area is the sum of the areas of the square base and the 4 congruent triangular faces.
SA = b^2 + 4 * bh/2
SA = (5 in.)^2 + 4 * (5 in.)(9 in.)/2
SA = 25 in.^2 + 2 * 45 in.^2
SA = 115 in.^2
Jacobi wants to install an underground sprinkler system in her backyard the backyard is rectangular with side length 17 m and 26 m .the water pipe will run diagonally across the yard about how many metres of water pipe does Jacobi need .
Answers
The length of the pipe required would be 31.06 meters
The length of the pipe is the hypotenus of the triangle formed :
hypotenus = √opposite² + adjacent²substituting the values into our equation:
length of pipe = √17² + 26²
length of pipe = √965 = 31.06
Therefore, the length of the pipe needed is 31.06 meters
Learn more on length : https://brainly.com/question/2217700
#SPJ1
Which quadratic equations have two solutions? Check all that apply.
y = x^2 + 3
y = x^2 - 8x - 20
y = x^2 - 25
y = 4x^2 + 12x + 9
y = -x^2 + 2x - 1
y = -2x^2 - 5x - 4
Answers
y = x^2 - 8x - 20 where x= -2 and 10
y = x^2 - 25 where x= -5 and 5
Use logarithmic differentiation to find the derivative of the function y=x^2x
Answers
The derivative of the function y = x^2x using logarithmic differentiation is dy/dx = x^2x(2 + 2ln(x)).
To find the derivative of the function y = x^2x using logarithmic differentiation, we follow these steps:
Take the natural logarithm of both sides of the equation:ln(y) = ln(x^2x)Apply the logarithmic property to simplify the equation:ln(y) = (2x)ln(x)Differentiate both sides of the equation implicitly:(1/y) * dy/dx = (2x)(1/x) + ln(x)(d/dx)(2x)Simplify the equation:(1/y) * dy/dx = 2 + 2ln(x)Multiply both sides of the equation by y:dy/dx = y(2 + 2ln(x))Substitute the original function back into the equation:dy/dx = x^2x(2 + 2ln(x))Learn more:About logarithmic differentiation here:
https://brainly.com/question/32030515
#SPJ11
To find the derivative of the function y = x^(2x) using logarithmic differentiation, we take the natural logarithm of both sides, apply logarithmic properties, and then differentiate implicitly.
Start by taking the natural logarithm of both sides of the equation:
ln(y) = ln(x^(2x))
Apply the power rule of logarithms to simplify the expression:
ln(y) = 2x * ln(x)
Now, differentiate both sides of the equation implicitly with respect to x:
(1/y) * dy/dx = 2 * ln(x) + 2x * (1/x)
Simplify the expression:
(1/y) * dy/dx = 2 * ln(x) + 2
Multiply both sides by y to isolate dy/dx:
dy/dx = y * (2 * ln(x) + 2)
Substitute the original value of y = x^(2x) back into the equation:
dy/dx = x^(2x) * (2 * ln(x) + 2)
The derivative of the function y = x^(2x) using logarithmic differentiation is dy/dx = x^(2x) * (2 * ln(x) + 2). Logarithmic differentiation is a useful technique for differentiating functions that involve exponentials or complicated algebraic expressions, as it allows us to simplify the calculation by taking the logarithm of both sides and then differentiating implicitly.
To know more about function visit:
https://brainly.com/question/11624077
#SPJ11
Determine where f'(z) exists and find its value when f(z) = x² + y²
Answers
The derivative of f(z) exists for all z in the complex plane at a value of f'(z) = 2x + 2y.
How to determine value?This is because f(z) is a polynomial, and polynomials are differentiable everywhere. The value of f'(z) is given by:
f'(z) = 2x + 2iy
where x and y are the real and imaginary parts of z.
To see this, use the definition of the derivative to find the limit of f(z + h) - f(z) as h approaches 0. This gives:
\(f'(z) = \lim_{h \to \ 0} (f(z + h) - f(z)) / h\)
Since f(z) is a polynomial, expand the expression in the numerator as follows:
\(f(z + h) - f(z) = (x + h)^2 + (y + h)^2 - x^2 - y^2\)
Simplifying the expression in the numerator gives us:
\(f(z + h) - f(z) = 2x h + 2y h + h^2\)
Dividing by h and taking the limit as h approaches 0 gives us:
f'(z) = 2x + 2y
as expected.
Find out more on polynomials here: https://brainly.com/question/4142886
#SPJ4
SOMEONE PLS HELP IM FAILING

Answers
write the (exact) area under a curve as a limit of riemann sums and (for certain curves) evaluate that limit.
Answers
The area under a curve can be written as a limit of Riemann sums. Riemann sums are used to estimate the area of a curve. To find the area of a curve, it is divided into small rectangles whose combined areas approximate the area of the curve. The limit of the sum of the areas of these rectangles is the exact area of the curve.
The Riemann sum is given by the formula:
Riemann sum = (b-a)/n ∑ f(xi)
The limit of the Riemann sum is given by the formula:
lim [ (b-a)/n ∑ f(xi) ]
The limit of the Riemann sum gives the precise area under a curve. Unfortunately, the limit can only be determined for specific curves. For example, if the curve is described by a simple function like y = x2 or y = sin(x), the limit may be calculated using calculus. Riemann sums may be used to estimate the area of a curve by splitting it into a finite number of rectangles of equal width.
The area of each rectangle is then determined by multiplying the height of the curve by the width of the rectangle. Summing the areas of each rectangle yields the overall area. The precise area under a curve is the limit of the Riemann sum. Nonetheless, the limit can be exceeded. The limit of the Riemann sum is the exact area under a curve. However, the limit can only be evaluated for certain curves using calculus.
Learn more about Riemann sums:
https://brainly.com/question/30766300
#SPJ11
first, carry out a regression of variable of "married dummy" on the variable "proportion". name that exhibit 1
Answers
By conducting this regression analysis, you will gain insights into how the "proportion" variable influences the likelihood of being married.
To carry out a regression of the variable "married dummy" on the variable "proportion" and name it as Exhibit 1, you would use statistical software such as R, Python, or Excel. The "married dummy" variable should be coded as 0 or 1, where 0 represents unmarried and 1 represents married individuals. The "proportion" variable represents the proportion of a specific characteristic, such as income or education level.
Using the regression analysis, you can determine the relationship between the "married dummy" variable and the "proportion" variable. The regression model will provide you with coefficients that indicate the magnitude and direction of the relationship.
Since you specifically asked for a long answer of 200 words, I will provide additional information. Regression analysis is a statistical technique that helps to understand the relationship between variables. In this case, we are interested in examining whether the proportion of a certain characteristic differs between married and unmarried individuals.
The regression model will estimate the intercept (constant term) and the coefficient for the "proportion" variable. The coefficient represents the average change in the "married dummy" variable for each one-unit increase in the "proportion" variable.
The regression output will also include statistics such as R-squared, which indicates the proportion of variance in the dependent variable (married dummy) that can be explained by the independent variable (proportion). Additionally, p-values will indicate the statistical significance of the coefficients.
Know more about the regression
https://brainly.com/question/13266116
#SPJ11
Volume of a Cylinder

Answers
Answer:
V = A h.
Since the area of a circle = π r 2 , then the formula for the volume of a cylinder is:
V = π r 2 h.
Step-by-step explanation:
The mean life of a television set is 123 months with a standard deviation of 19 months. If a sample of 55 televisions is randomly selected, what is the probability that the sample mean would differ from the true mean by greater than 1.2 months? I just need help getting from 1 - P (-0.47 < z < 0.47) to the answer. In my lesson it says the next step is 0.3192 but I have NO CLUE where that number comes from. Please help me! Thank you!
Answers
Answer:
1- P(-0.47 < z < 0.47) = 0.63836
Step-by-step explanation:
Here, we want to get the answer to;
1-P ( -0.47 < z < 0.47)
Mathematically, we are going to use the standard normal distribution table for this
Let us try to evaluate;
P(-0.47 < z < 0.47)
Mathematically, that will be;
P (z < 0.47) - P(z < -0.47)
where P (z < -0.47) = P( z > 0.47)
so we have
P(-0.47 < z < 0.47) = P(z < 0.47) - P(z > 0.47)
So we have this using the standard normal distribution table as follows;
0.68082 - 0.31818 = 0.36164
Now, we can insert this in the earlier expression of;
1- P(-0.47 < z < 0.47)
= 1-0.36164 = 0.63836
system properties, lss midterm 2, fall 2018 short answer). (a) consider a system with laplace transform h(s) = s 1 s2 s −20 . (1) is this system lowpass or bandpass? explain your reasoning.
Answers
The system described by the Laplace transform h(s) = s / (s^2 + s – 20) is a bandpass system.
To determine if a system is lowpass or bandpass, we examine the poles of its transfer function. In this case, the denominator of the Laplace transform represents the characteristic equation of the system.
The roots of the characteristic equation can help us identify the system’s frequency response. If the roots are real and negative, the system is lowpass. If the roots are complex conjugate pairs with positive real parts, the system is bandpass.
For the given system, we need to find the roots of the denominator: s^2 + s – 20 = 0. By factoring or using the quadratic formula, we find the roots to be s = 4 and s = -5.
Since the roots are real and have different signs (+4 and -5), the system is not lowpass. Instead, it is a bandpass system because it allows a range of frequencies to pass while attenuating others.
Learn more about Laplace transform here: brainly.com/question/31689149
#SPJ11
You would like to add freshly made mint ice cream to your restaurant's menu, and
have decided to grow your own mint. Last month, your mint plant was 2 feet, 7
inches tall. You took care of the mint plant properly, and that care has paid off.
This month, it is 4 feet, 1 inch tall. How much did it grow?
Answers
Explanation:
1 foot = 12 inches
3 ft 13 in - this month ( 4ft 1in)
- 2 ft 7 in - last month
——————
1 ft 6 in
Solve the equation for x and find the restrictions on the variable. Ax + bx = c
Answers
Answer:
x = c/(A + b)
A + b ≠ 0
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
Brackets Parenthesis Exponents Multiplication Division Addition Subtraction Left to RightEquality Properties
Algebra I
FactoringStep-by-step explanation:
Step 1: Define
Ax + bx = c
Step 1: Solve for x
Factor: x(A + b) = cIsolate x: x = c/(A + b)We know that we cannot divide by 0, so A + b cannot equal 0.
Find the distance from the vector (1, 2, 3, 4) to the
subspace of R^4 spanned by the vectors (1, −1, 1, 0) and (3, 2, 2,
1).
Answers
The distance from the vector (1, 2, 3, 4) to the subspace of R^4 spanned by the vectors (1, -1, 1, 0) and (3, 2, 2, 1) can be calculated as the length of the orthogonal projection of (1, 2, 3, 4) onto the subspace.
To find the distance, we first need to determine the orthogonal projection of the vector (1, 2, 3, 4) onto the subspace spanned by (1, -1, 1, 0) and (3, 2, 2, 1).
The orthogonal projection of (1, 2, 3, 4) onto the subspace can be obtained by projecting (1, 2, 3, 4) onto each of the spanning vectors and then summing those projections. Using the projection formula, we find that the projection of (1, 2, 3, 4) onto the first spanning vector (1, -1, 1, 0) is (5/3, -5/3, 5/3, 0), and the projection onto the second spanning vector (3, 2, 2, 1) is (3/2, 1, 1, 1/2).
Next, we calculate the difference vector between (1, 2, 3, 4) and the sum of the two projections: (1, 2, 3, 4) - [(5/3, -5/3, 5/3, 0) + (3/2, 1, 1, 1/2)] = (2/6, 13/6, 7/6, 7/2).
Finally, we find the length of the difference vector, which represents the distance between (1, 2, 3, 4) and the subspace: √[(2/6)^2 + (13/6)^2 + (7/6)^2 + (7/2)^2] = √(242/9).
Therefore, the distance from the vector (1, 2, 3, 4) to the subspace of R^4 spanned by (1, -1, 1, 0) and (3, 2, 2, 1) is √(242/9).
To learn more about orthogonal click here:
brainly.com/question/32196772
#SPJ11