Answers
Answer:
15
Step-by-step explanation:
Answer:
Step-by-step explanation:
three units <3
Related Questions
What is the end behavior of f(x)=5x^3-2x+5

Answers
Answer:
A
Step-by-step explanation:
positive leading coefficient means increasing

Find the exact value of cos 135° sin15°.
Answers
Answer:
its cos 50
Step-by-step explanation:
amen
HELPPP!!!!!!!!!!!!!!!! PLEASE! :D

Answers
Answer:
The solution to the inequality is:
\(-1\le \:x\le \:3\)
The line graph of the solution is also attached.
Step-by-step explanation:
Given the expression
\(4x-1\:\le \:5x\:\le \:3\left(x+2\right)\)
solving the expression
\(4x-1\:\le \:5x\:\le \:3\left(x+2\right)\)
\(\mathrm{If}\:a\le \:u\le \:b\:\mathrm{then}\:a\le \:u\quad \mathrm{and}\quad \:u\le \:b\)\(4x-1\le \:5x\quad \mathrm{and}\quad \:5x\le \:3\left(x+2\right)\)
solving
\(4x-1\le \:5x\)
Add 1 to both sides
\(4x-1+1\le \:5x+1\)
Simplify
\(4x\le \:5x+1\)
Subtract 5x from both sides
\(4x-5x\le \:5x+1-5x\)
simplify
\(-x\le \:1\)
Multiply both sides by -1 (reverse inequality)
\(\left(-x\right)\left(-1\right)\ge \:1\cdot \left(-1\right)\)
Simplify
\(x\ge \:-1\)
Similarly solving
\(5x\le \:3\left(x+2\right)\)
Subtract 3x from both sides
\(5x-3x\le \:3x+6-3x\)
Simplify
\(2x\le \:6\)
Divide both sides by 2
\(\frac{2x}{2}\le \frac{6}{2}\)
Simplify
\(x\le \:3\)
So combine the interval
\(x\ge \:-1\quad \mathrm{and}\quad \:x\le \:3\)
Merge overlapping intervals
\(-1\le \:x\le \:3\)
Therefore, the solution to the inequality is:
\(-1\le \:x\le \:3\)
The line graph of the solution is also attached.

Enter the correct answer in the box. What standard form polynomial expression represents the perimeter of this quadrilateral? 3x– 4x + 3 4x3 + 2x x² – 2x x2 + 6x - 11

Answers
Answer:
5^3+4^2-8
Step-by-step explanation:
Answer:
5^3+4^2-8
Step-by-step explanation:
14. (10.0 points) Given f(x)=sin(2πx), when x = 0.3, f(x) = 0.951057. Approximate the value of f(0.2) using the first two terms in the Taylor series and Vx=0.1. (Write your answer to 6 decimal points).
Answers
Given the function f(x)=sin(2πx), with x = 0.3, f(x) = 0.951057. The objective is to approximate the value of f(0.2) using the first two terms in the Taylor series and Vx=0.1.
We know that the Taylor series for a function f(x) can be written as:f(x)=f(a)+f′(a)(x−a)+f′′(a)2(x−a)2+…+f(n)(a)n!(x−a)n+…The first two terms of the Taylor series are given by:f(x)=f(a)+f′(a)(x−a)The first derivative of f(x) is given by:f′(x)=2πcos(2πx)On substituting x = a = 0.1, we get:f′(0.1) = 2πcos(2π * 0.1) = 5.03118603447The value of f(x) at a=0.1 is given by:f(0.1) = sin(2π * 0.1) = 0.587785252292With a=0.1, the first two terms of the Taylor series become:f(x)=0.587785252292+5.03118603447(x−0.1) = 0.587785252292+0.503118603447x−0.503118603447×0.1Using x=0.2 and substituting the values of a and f(a) in the equation above, we get:f(0.2)=0.587785252292+0.503118603447*0.2−0.503118603447×0.1=0.712261After approximating the value of f(0.2) using the first two terms in the Taylor series,
we can conclude that the value of f(0.2) = 0.712261 with a = 0.1, with an error of approximately 0.012796.
To know more about Taylor series visit
https://brainly.com/question/32235538
#SPJ11
LAST QUESTION please just help me out please

Answers
999-
Someone explain please

Answers
Answer:
SA = 94 ft²
Step-by-step explanation:
To find the surface area of a rectangular prism, you can use the equation:
SA = 2 ( wl + hl + hw )
SA = surface area of rectangular prism
l = length
w = width
h = height
In the image, we are given the following information:
l = 4
w = 5
h = 3
Now, let's plug in the information given to us to solve for surface area:
SA = 2 ( wl + hl + hw)
SA = 2 ( 5(4) + 3(4) + 3(5) )
SA = 2 ( 20 + 12 + 15 )
SA = 2 ( 47 )
SA = 94 ft²
If this answer helped you, please leave a thanks!
Have a GREAT day!!!
what is the largest integer less than $2010$ that has a remainder of $5$ when divided by $7,$ a remainder of $10$ when divided by $11,$ and a remainder of $10$ when divided by $13$?
Answers
The largest integer less than 2010 that has a remainder of 5 when divided by 7, a remainder of 10 when divided by 11, and a remainder of 10 when divided by 13. is 1440
Given, a number less than 2010 that has a remainder of 5 when divided by 7, a remainder of 10 when divided by 11, and a remainder of 10 when divided by 13.
On using the Chinese remainder theorem. As, the numbers 7, 11, 13 are pairwise coprime.
Firstly, an integer m such that m−5 is divisible by 7 and m−10 is divisible by 11 .
The Chinese remainder theorem says that all integers that work will be of the form 54+7⋅11⋅k=54+77k for any integer k .
Next an integer n such that n−10 is divisible by 13 and n−54 is divisible by 77.
Then, by the Chinese remainder theorem, all the integers that also work are of the form 439+13⋅77⋅k=439+1001k .
Hence, the positive integers satisfying the condition are: 439, 439 + 1001 = 1440, 1440 + 1001 = 2441, and so on.
The largest integer less than 2010 is 1440.
Learn more about Chinese Remainder Theorem here https://brainly.com/question/10074520
#SPJ4
a poker player has either good luck or bad luck each time she plays poker. she notices that if she has good luck one time, then she has good luck the next time with probability 0.5 and if she has bad luck one time, then she has good luck the next time with probability 0.4. what fraction of the time in the long run does the poker player have good luck? g
Answers
The fraction of time in the long run that the poker player has good luck is 0.8 or 80%.
Let's use the law of total probability to calculate the fraction of time in the long run that the poker player has good luck.
Let G denote the event that the poker player has good luck, and B denote the event that she has bad luck. Then we have:
P(G) = P(G|G)P(G) + P(G|B)P(B)
From the problem statement, we know that if the poker player has good luck one time, then she has good luck the next time with probability 0.5, which means P(G|G) = 0.5. Similarly, if she has bad luck one time, then she has good luck the next time with probability 0.4, which means P(G|B) = 0.4.
We don't know the value of P(G) yet, but we can use the fact that P(G) + P(B) = 1. So we can write:
P(G) = P(G|G)P(G) + P(G|B)(1 - P(G))
Substituting the values we know, we get:
P(G) = 0.5P(G) + 0.4(1 - P(G))
Simplifying and solving for P(G), we get:
P(G) = 0.8
Therefore, the fraction of time in the long run that the poker player has good luck is 0.8 or 80%.
To learn more about probability, click here:
https://brainly.com/question/30034780
#SPJ11
What two things must DNA be able to do?
Answers
DNA contains the instructions needed for an organism to develop, survive and reproduce. To carry out these functions, DNA sequences must be converted into messages that can be used to produce proteins, which are the complex molecules that do most of the work in our bodies. Hope this helps!
How do you find the median of a class?
Answers
In a grouped data,
it is not possible to find the median for the given observation by looking at the cumulative frequencies.
The middle value of the given data will be in some class interval. So, it is necessary to find the value inside the class interval that divides the whole distribution into two halves.
In this scenario, we have to find the median class.
To find the median class, we have to find the cumulative frequencies of all the classes and n/2.
After that, locate the class whose cumulative frequency is greater than (nearest to) n/2. The class is called the median class.
After finding the median class, use the below formula to find the median value.
\(Median = l +(\frac{\frac{n}{2}- cf}{f} )*h\)
Where
l is the lower limit of the median class
n is the number of observations
f is the frequency of median class
h is the class size
cf is the cumulative frequency of class preceding the median class.
To know more about median class visit brainly.com/question/18845760
#SPJ4
May I please get some help on these



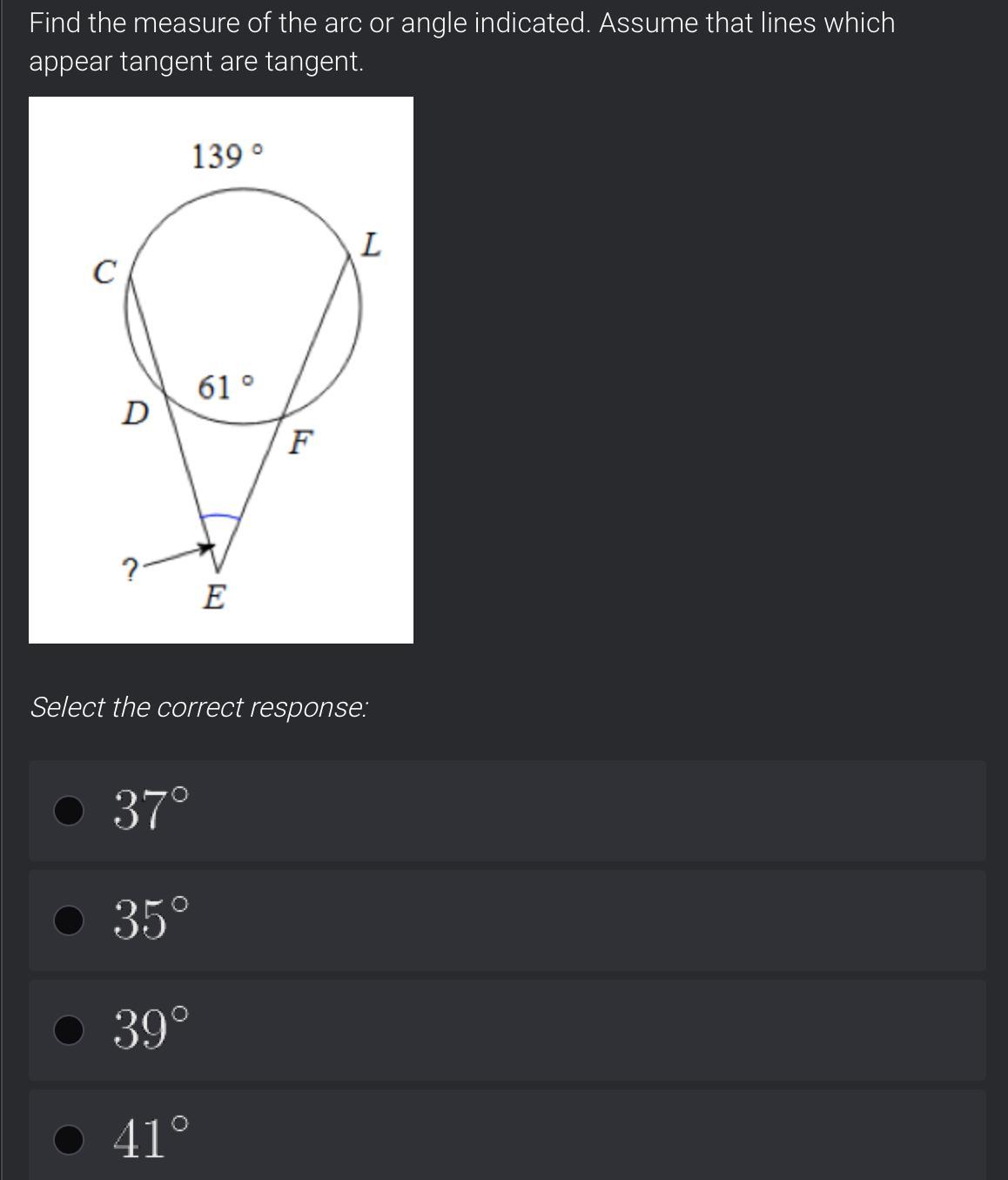

Answers
Answer:
The Correct answer is
57°
i am interested in whether listening to vance joy makes people feel happier. i hypothesize that people that listen to vance joy will have higher levels of happiness than people who do not listen to vance joy. on a normal curve distribution, where would the critical region(s) be located?
Answers
The critical region(s) on a normal curve distribution would be located in the tail(s) of the curve. In hypothesis testing, the critical region(s) refers to the area(s) of the distribution that corresponds to rejecting the null hypothesis. This region(s) is based on the significance level of the test, which is typically set at 0.05 or 0.01.
In this case, the null hypothesis would be that listening to Vance Joy does not have a significant effect on happiness levels. The alternative hypothesis, which is what the researcher is testing for, would be that there is a significant difference in happiness levels between those who listen to Vance Joy and those who do not.
Assuming a two-tailed test, where the researcher is interested in whether the effect could be positive or negative, the critical region(s) would be located in both tails of the normal curve distribution. The exact location of the critical region(s) would depend on the sample size and the significance level of the test.
If the sample size is large, the critical region(s) would be located farther from the mean, indicating a higher level of confidence in rejecting the null hypothesis. Conversely, if the sample size is small, the critical region(s) would be located closer to the mean, indicating a lower level of confidence in rejecting the null hypothesis.
Overall, the critical region(s) on a normal curve distribution represents the area(s) of the distribution that corresponds to rejecting the null hypothesis, and its location depends on the sample size and the significance level of the test.
for more such question on hypothesis
https://brainly.com/question/606806
#SPJ11
Maura spends $5.50 in materials to make a scarf. She sells each scarf for 600% of the cost of materials.
Complete the sentence by selecting the correct word from the drop down choices.
Maria sells each scarf for Choose... ✓ or

Answers
The price that Maura sell each scarf would be =$33. Maura sells each scarf for $33. That is option A.
How to calculate the selling price of each scarf?To calculate the amount of money that Maura spends on each scarf the following is carried out.
The amount of money that she spends on the scarf material = $5.50
The percentage selling price of each scarf = 600% of $5.50
That is ;
= 600/100 × 5.50/1
= 3300/100
= $33.
Therefore, each price that is sold by Maura would probably cost a total of $33.
Learn more about cost price here:
https://brainly.com/question/26008313
#SPJ1
what is the answer to 3x + 7x − 2
Answers
Answer:
Step-by-step explanation:
Add like terms. 3x & 7x are like terms
3x +7x - 2 = 10x - 2
Answer:
0.2
Step-by-step explanation:
3x+7x-2
3x+7x-2=0
3x+7x=2
10x=2
x=2/10
x=\(\frac{1}{5}\)
how is solving |ax| + b = c different from solving |ax+b| = c?
Answers
Step-by-step explanation:
they are different because the first equation only ax is in absolute but in the second equation both ax and b are in absolute, so we could solve them differently.
When a car's brakes are applied, it travels 7 feet less in each second than the previous second until it comes to a complete stop. A car goes 28 feet in the first second after the brakes are applied. How many feet does the car travel from the time the brakes are applied to the time the car stops?
Answers
Answer:
70feet
Step-by-step explanation:
during the
1st sec it travels 28 ft
2nd sec =28-7=21ft
3rd sec= 21-7=14ft
4th sec= 14-7= 7ft
last sec=7-7=0ft, at this point the car stops.
so altogether it travels 28+21+14+7+0= 70 feet
Pls help, my moms gonna tell if i fail

Answers
Answer:
0 and 3, I think those are the answers cause they make the most sense
Step-by-step explanation:
Find the volume generated by rotating the region bounded by y = 6 sin(x), y = 0, x = 27, and r = 37, about the y-axis. Express your answer in terms of . Volume =
Answers
Given the curve, y = 6 sin x, y = 0, x = 27, and r = 37,which bound the region to be rotated about the y-axis.
We have to find the volume generated by rotating the region about the y-axis.
Therefore, the formula for the volume of the solid of revolution is given by:
V = π∫[a, b] f²(y) dy
Here, a = 0 and b = 27, and f (y) is the inverse of the function x = 6 sin x.
So, y = 6 sin x is equivalent to
x = sin⁻¹(y/6),
which is the inverse function of y = 6 sin x.
Therefore, we have:
f(y) = sin⁻¹(y/6)
The radius of revolution is given by the distance between the y-axis and the curve.
Therefore,r = x = sin⁻¹(y/6) + 37
Thus, the formula for the volume is given by:
V = π∫[0, 6] (sin⁻¹(y/6) + 37)² dy
Here, we use u-substitution,
let u = sin⁻¹(y/6) + 37,
therefore du/dy
= 1/√[1 - (y/6)²]6(du)
= (1/√[1 - (y/6)²]) dy
Therefore, the integral becomes:
V = π ∫[37, 37.1] u² sin⁻¹(u - 37)
du = 5.068 π cubic units
The value of V is expressed in terms of π, which is the exact form of the volume generated by rotating the region about the y-axis.
Therefore, the volume of the solid of revolution is 5.068 π cubic units.
To know more about cubic units, visit:
https://brainly.com/question/29130091
#SPJ11
I’m so confused about this problem:
1 5/9 ÷ -1/2
Can anyone help me?
(ToT)
Answers
Answer: -3.11111112
Step-by-step explanation:
1 and 5/9 as a decimal is 1.555555556
-1/2 as a decimal is -0.5
1.555555556 divided by -0.5 is -3.11111112
how will the z-scores compare if you use your height in inches verses centimeters?
Answers
The z-scores will remain the same regardless of whether you use inches or centimetres for the height measurements.
The z-scores will not change if you convert the height measurements from inches to centimetres or vice versa. The z-score is a standard score representing the number of standard deviations, a value above or below the mean of a normal distribution.
The z-score is calculated using the formula z = (x - mean)/standard deviation, where x is the value being compared to the mean and standard deviation of the distribution.
Converting the height from inches to centimetres or vice versa will only change the units of measurement, but the relative position of a value within the distribution will remain unchanged.
Therefore, the z-scores will remain the same regardless of whether you use inches or centimetres for the height measurements.
To know more about z-scores, here
https://brainly.com/question/15016913
#SPJ4
Question Homework: Homework 4 18, 6.1.32 39.1 of 44 points Part 2 of 2 Save Points: 0.5 of 1 Assume that a randomly selected subject is given a bone density test. Those test scores are normally distri
Answers
Assuming that a randomly selected subject is given a bone density test, the test scores are normally distributed with a mean score of 85 and a standard deviation of 12.
This means that 68% of subjects have bone density test scores within one standard deviation of the mean, which is between 73 and 97.
The probability of randomly selecting a subject with a bone density test score less than 60 is 0.0062 or 0.62%.
Given: Mean = 85
Standard Deviation = 12
Using the standard normal distribution table, we find that the probability of z being less than -2.08 is 0.0188.
Therefore, the probability of a randomly selected subject being given a bone density test, with a score less than 60 is 0.0188 or 1.88%.
Summary: The given problem is related to the probability of a randomly selected subject being given a bone density test with a score less than 60. Here, we have used the standard normal distribution table to calculate the probability. The calculated probability is 0.0188 or 1.88%.
Learn more about probability click here:
https://brainly.com/question/13604758
#SPJ11
1 = 5x + 2; w = x^2 + 1
Can someone help me with this question?;(
Answers
So if x is -1/5 then substitute it into the second equation and you get W=11/9
Hope this helps x
Answer:
5x^3 + 5x+ 2x^2 + 2
Step-by-step explanation:
(5x+2)(x^2+1)
5x^3 + 5x+ 2x^2 + 2
what is the remainder when 2202 202 is divided by 2101 251 1? (2020amc10b problem 22) (a) 100 (b) 101 (c) 200 (d) 201 (e) 202
Answers
To solve this problem, we can use the Chinese Remainder Theorem. We need to find the remainder when 2202 202 is divided by both 2101 and 251.
First, note that 2101 and 251 are relatively prime. Therefore, by the Chinese Remainder Theorem, there exists a unique remainder between 0 and 2101 * 251 - 1 (inclusive) that satisfies the two conditions.
To find this remainder, we can use the remainders when 2202 202 is divided by 2101 and 251.
Note that 2202 is congruent to 101 (mod 2101) and 0 (mod 251). Therefore, we can use the Chinese Remainder Theorem to find that the remainder when 2202 202 is divided by 2101 * 251 is congruent to:
101 * (251^2) * (251^(-1)) + 0 * (2101^2) * (2101^(-1)) (mod 2101 * 251)
Using the fact that 251^(-1) is congruent to 201 (mod 2101) and 2101^(-1) is congruent to 1922 (mod 251), we can simplify this expression to:
101 * (251^2) * (201) + 0 * (2101^2) * (1922) (mod 2101 * 251)
Simplifying further, we get:
101 * 251 * 201 (mod 2101 * 251)
This is congruent to 101 * 201 (mod 251), which is congruent to 101 (mod 251).
Therefore, the remainder when 2202 202 is divided by 2101 251 1 is 101, which is option (b).
Learn more about Remainder Theorem here:- brainly.com/question/30242306
#SPJ11
The total cost of owning a home for 6 years is $120,000. The
rent for a comparable home is $1500 per month. If you had invested the
down payment for the home, you could have earned $10,000 in interest.
After 6 years, how much more, in dollars, is the cost of owning compared
to the cost of renting?
Answers
After 6 years, the difference between owning the house and renting is $12,000.
What is the difference in owing and renting the house?
The first step is to determine the total cost of renting the house for six years.
Total cost of renting the house = rent per month x number of years x number of months in a year
1500 x 12 x 6 = $108,000
Difference = cost of owning - cost of renting
$120,000 - $108,000 = $12,000
To learn more about subtraction, please check: https://brainly.com/question/854115
#SPJ1
The price of an item yesterday was $60. Today, the price fell to $42. Find the percentage decrease.
Answers
Answer:
-30% or 30% decrease
Step-by-step explanation:
What's percentage decrease?
Percent decrease is the difference between the initial value and new value, indicating a loss of value. The formula to find percent decrease is \(\frac{NV-IV}{IV} * 100\), where NV = new value and IV = initial value.How do we solve this problem?
We know that the original value was $60, so that represents IV. Also, now that the price is $42, it represents NV. Now, we plug in the values!\(\frac{42-60}{60} * 100\) \(\frac{-18}{60} * 100\) \(-\frac{3}{10} * 100\) \(-3 * 10\) \(-30\)Therefore, the answer is 30% decrease.
The velocity function of a particle moving along a line is v()-2-9-1+8, where is in seconds and v is in mysec. Find the displacement and the distance traveled by the particle during the time interval [-3,9].
Answers
The displacement of the particle during the time interval [-3, 9] is 48 mysec in the positive direction. The distance traveled by the particle during this time interval is 72 mysec.
To find the displacement of the particle, we need to integrate the velocity function with respect to time over the given time interval. Integrating the function v(t) = -2t - 9t^2 - t + 8, we get the displacement function as d(t) = -t^2 - 3t^3/3 - t^2/2 + 8t + C, where C is the constant of integration. To find C, we evaluate the displacement at t = -3, which gives us d(-3) = 9 + 27/3 + 9/2 - 24 + C = 0. Solving for C, we find C = -12. The displacement at t = 9 is then calculated as d(9) = -81 - 729/3 - 81/2 + 72 - 12 = 48 mysec in the positive direction.
To find the distance traveled by the particle, we consider the absolute value of the velocity function and integrate it over the time interval [-3, 9]. Taking the absolute value of v(t) = -2t - 9t^2 - t + 8, we have |v(t)| = 2t + 9t^2 + t - 8. Integrating this function over [-3, 9], we find the distance traveled as |d(t)| = 2t^2/2 + 9t^3/3 + t^2/2 - 8t + D, where D is the constant of integration. Evaluating |d(t)| at t = -3, we get |d(-3)| = 18/2 + 27/3 + 9/2 + 24 + D = 72 + D. Therefore, the distance traveled by the particle during the time interval [-3, 9] is 72 mysec.
Learn more about integrate here:
https://brainly.com/question/31744185
#SPJ11
9. please please help me out ill mark you brainlist

Answers
Answer:
C. The scale factor is less than one.
Step-by-step explanation:
By definition, similar triangles have equal angles and proportional corresponding side lengths. Thus, A, B, and D are all mutually exclusive, leaving C the only possible answer. Upon further inspection, the scale factor is indeed greater than one (each side length is scaled by a factor of two, which is large than one)
The peanuts cost $2.70 for 1 pound. How
much does 3.5 pounds of peanuts cost?
Answers
Answer: $9.45
Step-by-step explanation:
Set up a proportion of 2.70/1 = x/3.5. To solve, multiply 2.70 by 3.5 and divide by 1. 2.70*3.5 = 9.45/1 = 9.45.
Take 2.70 times 3.5 and you get your answer.
The scores earned in a flower-growing competition are represented in the stem-and-leaf plot.
2 0, 1, 3, 5, 7
3 2, 5, 7, 9
4
5 1
6 5
Key: 2|7 means 27
What is the appropriate measure of variability for the data shown, and what is its value?
The IQR is the best measure of variability, and it equals 16.
The range is the best measure of variability, and it equals 45.
The IQR is the best measure of variability, and it equals 45.
The range is the best measure of variability, and it equals 16.
Answers
The appropriate measure of variability for the given data is the IQR, and its value is 16.
Based on the given stem-and-leaf plot, which represents the scores earned in a flower-growing competition, we can determine the appropriate measure of variability for the data.
The stem-and-leaf plot shows the individual scores, and to measure the spread or variability of the data, we have two commonly used measures: the range and the interquartile range (IQR).
The range is calculated by subtracting the smallest value from the largest value in the dataset. In this case, the smallest value is 20, and the largest value is 65. Therefore, the range is 65 - 20 = 45.
The interquartile range (IQR) is a measure of the spread of the middle 50% of the data. It is calculated by subtracting the first quartile (Q1) from the third quartile (Q3). Looking at the stem-and-leaf plot, we can identify the quartiles. The first quartile (Q1) is 25, and the third quartile (Q3) is 41. Therefore, the IQR is 41 - 25 = 16.
In this case, both the range and the IQR are measures of variability, but the IQR is generally preferred when there are potential outliers in the data. It focuses on the central portion of the dataset and is less affected by extreme values. Therefore, the appropriate measure of variability for the given data is the IQR, and its value is 16.
For more questions on variability
https://brainly.com/question/14544205
#SPJ8
