Answers
Answer:
89/3
Stp/lanation:
Related Questions
HELP ASAP ILL GIVE BRAINLIST
t/f If substituting the test point produces a false solution, we shade on the opposite side of the line.
t/f Elimination will give you an exact answer to a system of equations.
Answers
Answer:
TRUE If substituting the test point produces a false solution, we shade on the opposite side of the line.
FALSE Elimination will give you an exact answer to a system of equations.
Step-by-step explanation:
Weird, I thought I already answer this xD
A plane is descending onto the runway with an angle of depression of 55°. If it has 2.8 miles to go before landing (hypotenuse), what is the current altitude of the plane?
A. 4.9 miles
B. 3.4 miles
C. 4 miles
D. 1.6 miles
E. 2.3 miles
Answers
Answer:
Option C is correct
Step-by-step explanation:
Given: A plane is descending onto the runway with an angle of depression of 55°. Also, it has 2.8 miles to go before landing.
To find: current altitude of the plane
Solution:
Consider the attached image.
In ΔABC,
\(\angle ACB=55^{\circ}\) (Alternate interior angles)
For any angle \(\theta\),
\(tan \theta\) = side opposite to angle/side adjacent to angle
\(\tan C=\frac{AB}{BC}\)
Put \(\angle C=55^{\circ}\,,\,BC=2.8\,\,miles\)
\(AB=2.8\,\tan 55^{\circ}=3.999\approx 4\,\,miles\)
So, the current altitude of the plane is 4 miles.
trigonometry
its due in 20 minutes help

Answers
Answer:
Answer= 17.5 (B)
Step-by-step explanation:
This is tangent because TOA(opposite/adjacent)
On your calculator, do side length(25) sin angle(35)=17.5
Answer to this is apparently
y=10(3.16)^x
Please show the work and I will give u the brainliest:))

Answers
Answer:
\(y=10(3.16)^x\)
Step-by-step explanation:
Given equation is,
log(y) = 0.5x + 1
We can rewrite this equation as,
\(\text{log}_{10}(y)=0.5x+1\)
y = \(10^{(0.5x+1)}\)
[If \(\text{log}_a(b)=c\), then \(b = a^{c}\)]
y = \(10(10)^{0.5x}\)
y = \(10[(10)^{0.5}]^x\)
y = \(10(3.16)^x\) [Since, \(10^{0.5}=3.16\)]
Therefore, \(y=10(3.16)^x\) will be the answer.
Two angles meet at a point on a straight line. One of the angles is 43o
. Work out the size of the other angle.
Answers
Answer:
d
Step-by-step explanation:
The model represents an equation. What value of x makes the equation true?

Answers
An equation is formed of two equal expressions. The value of x that can satisfy this equation is 1.875.
What is an equation?An equation is formed when two equal expressions are equated together with the help of an equal sign '='.
The model represents the equation as given below,
\((6 \times -x)+(6 \times 1) = (2 \times x) + (9 \times -1)\\\\-6x+6=2x-9\\\)
The value of x that can satisfy this equation can be written as,
\(-6x+6=2x-9\\\\-6x-2x=-9-6\\\\-8x = -15\\\\8x=15\\\\x = \dfrac{15}{8} = 1.875\)
Hence, the value of x that can satisfy this equation is 1.875.
Learn more about Equation:
https://brainly.com/question/2263981
#SPJ1
(This question may have more than one solution.) Let C be a fixed n × n matrix. Determine whether the following are linear
operators on R^X":
(a) L(A) = 1 - 1
(6) L(A) = 1 + 17
(c) L(1) = C1 + AC
(d) L(1) = C°1
(c) L(1) = 1?C
Answers
Functions (c) L(1) = C1 + AC and (d) L(1) = C°1 are linear operators on R^n, while functions (a), (b), and (e) do not satisfy the properties of linearity and therefore are not linear operators.
a) L(A) = 1 - 1: This function is not a linear operator because it does not preserve scalar multiplication. Multiplying A by a scalar c would yield L(cA) = c - c, which is not equal to cL(A) = c(1 - 1) = 0.
b) L(A) = 1 + 17: Similar to the previous case, this function is not linear since it fails to preserve scalar multiplication. Multiplying A by a scalar c would result in L(cA) = c + 17, which is not equal to cL(A) = c(1 + 17) = c + 17c.
c) L(1) = C1 + AC: This function is a linear operator since it satisfies both the preservation of addition and scalar multiplication properties. Adding matrices A and B and multiplying the result by scalar c will yield L(A + B) = C(1) + AC + C(1) + BC = L(A) + L(B), and L(cA) = C(1) + cAC = cL(A).
d) L(1) = C°1: This function is a linear operator since it satisfies the properties of linearity. Addition and scalar multiplication are preserved, and L(cA) = C(0)1 = c(C(0)1) = cL(A).
e) L(1) = 1?C: This function is not a linear operator as it does not preserve scalar multiplication. Multiplying A by a scalar c would give L(cA) = 1?(cC), which is not equal to cL(A) = c(1?C).
In summary, functions (c) L(1) = C1 + AC and (d) L(1) = C°1 are linear operators on R^n, while functions (a), (b), and (e) do not satisfy the properties of linearity and therefore are not linear operators.
Learn more about scalar multiplication here:
https://brainly.com/question/28875206
#SPJ11
The table shows values for functions f(x) and g(x). X f(x)=3x g(x)=2x 1 −2 19 −3 −1 13 −1 0 1 1 1 3 3 2 9 5 What is the solution to f(x)=g(x) ? Select each correct answer. X = −2 x = −1 x = 0 x = 1 x = 2.
Answers
By hit and trial of each option and also by graph, solutions to f(x) = 3ˣ and g(x)=2x-1 will be 0 and 1.
given functions are,
\(f(x) = 3^x\\\\g(x) = 2x+1\)
let us put x=0
f(0) = 1
g(0) = 1
f(0)=g(0)=1
so 0 will be a solution.
let us put x=1
f(1)= 3
g(1) = 3
f(1)=g(1)=3
so 1 will be also a solution
let us put x=2
f(2) = 9
g(2) = 5
f(2)≠g(2)
so 2 will not be solution.
x=-2 and x=-1 clearly will not be solution because,
g(-2) = negative value but f(x) cannot be negative, being an exponential function.
what is an exponential function?
Any function in form f(x)= pˣ, where p≥1, is called an exponential function.
therefore, solutions to f(x) = g(x) will be 0 and 1.
to get more about exponential function refer to:
https://brainly.com/question/2456547

Juan wants to pour 95.95 grams of salt into a container. So far, he has poured 37.6 grams. How much more salt should Juan pour?
grams
x
?
I Don't Know
Submit
2020 McGrawan Education All Rights Reserved
Answers
Answer:
58.35 grams
Step-by-step explanation:
All you need to do is subtract the amount of salt that has been poured from the amount that Juan wants
\(95.95-37.6= 58.35\)
Why is MATH important for everyday life. (Give 3 REAL examples on how it is used)
Answers
Mathematics is important for everyday life for several reasons. Budgeting, Cooking and baking, Time management.
Here are three real examples on how it is used:
Budgeting: Math is essential for managing personal finances, such as creating a budget, tracking expenses, and planning for the future. For instance, using math, we can calculate the amount of money we need to set aside for bills, rent, groceries, and other expenses. We can also use math to determine how much money we need to save each month to reach our long-term financial goals, such as buying a house, paying for college, or retiring comfortably.
Cooking and baking: Math is an essential part of cooking and baking. When we cook or bake, we need to use math to measure ingredients accurately, adjust recipe quantities based on the number of servings, and calculate cooking times and temperatures. For example, we may need to double or halve a recipe to serve a larger or smaller group of people, and we may need to convert units of measurement, such as ounces to grams or Fahrenheit to Celsius.
Time management: Math is also important for managing time effectively. We use math to calculate time differences, such as when scheduling appointments or meetings across different time zones. We can also use math to estimate how long tasks will take, such as how much time we need to complete a project, commute to work, or run errands. Using math, we can prioritize tasks based on their level of urgency and importance, and allocate time accordingly.
Learn more about Budgeting here
https://brainly.com/question/6663636
#SPJ11
I need help on my math work

Answers
The specified details of the triangle, obtained using the segments joining the midpoints of the sides of the triangle ΔADG and trapezoid ACFG indicates that we get;
4. \(\overline{CE}\) is a midsegment of ΔBDF
\(\overline{BF}\) is the midsegment of trapezoid ACFG
5. CE = 12 cm, AG = 36 cm
6. m∠2 = 116°, m∠3 = 32°, m∠4 = 58°, m∠5 = 58°, m∠6 = 64°
What is the midpoint of a segment?The midpoint of a segment or the side of a triangle is a point that divides the segment into two parts of the same length.
4. The details of the diagram indicates that the segment \(\overline{CE}\) is the midsegment of triangle ΔBDF
\(\overline{BF}\) is the midsegment of trapezoid ACFG
5. \(\overline{CD}\) is congruent to \(\overline{BC}\) by the definition of the midpoint of \(\overline{BD}\), similarly;
\(\overline{BC}\) is congruent to \(\overline{AB}\), by the definition of midpoint of \(\overline{AC}\), therefore;
\(\overline{CE}\) is the midsegment of triangle ΔBDF, therefore;
CE = (1/2) × BF
CE = (1/2) × 24 cm = 12 cm
CE = 12 cm
ΔBDF and ΔADG and ΔCDE are similar triangles, therefore;
\(\overline{BD}\) = (2/3) × \(\overline{AD}\)
Similarly, by the relationship between similar triangles we get;
\(\overline{BF}\) = (2/3) × \(\overline{AG}\)
BF = 24 cm, therefore;
24 = (2/3) × AG
AG = (3/2) × 24 = 36
AG = 36 cm
6. The length of a median of a right triangle, drawn from the right angled vertex, is half the length of the hypotenuse side.
Therefore; ΔACM and ΔABM are an isosceles triangles
m∠1 = m∠3 = 32°
m∠2 = 180° - (32° + 32°) = 116°
m∠2 = 116°
m∠3 = 32°
m∠4 = m∠5 = 90° - m∠1
m∠4 = m∠5 = 90° - 32° = 58°
m∠4 = 58°
m∠5 = 58°
m∠6 = 180° - (m∠4 + m∠5)
m∠6 = 180° - (58° + 58°) = 64°
m∠6 = 64°
Learn more on the midpoint of a segment here: https://brainly.com/question/8075904
#SPJ1
Please help 60 points for a rapid answer-In the figure below which of the following is true in circle E?


Answers
Answer:
all 3 options are true : A, B, C
Step-by-step explanation:
warning : it has come to my attention that some testing systems have an incorrect answer stored as right answer for this problem.
they say that A and C are correct.
but I am going to show you that if A and C are correct, then also B must be correct.
therefore, my given answer above is the actual correct answer (no matter what the test systems say).
originally the information about the alignment of the point F in relation to point E was missing.
therefore, I considered both options :
1. F is on the same vertical line as E.
2. F is not on the same vertical line as E.
because of optical reasons (and the - incomplete - expected correct answers of A and C confirm that) I used the 1. assumption for the provided answer :
the vertical line of EF is like a mirror between the left and the right half of the picture.
A is mirrored across the vertical line resulting in B. and vice versa.
the same for C and D.
this leads to the effect that all 3 given congruence relationships are true.
if we consider assumption 2, none of the 3 answer options could be true.
but if the assumptions are true, then all 3 options have to be true.
now, for the "why" :
remember what congruence means :
both shapes, after turning and rotating, can be laid on top of each other, and nothing "sticks out", they are covering each other perfectly.
for that to be possible, both shapes must have the same basic structure (like number of sides and vertices), both shapes must have the same side lengths and also equally sized angles.
so, when EF is a mirror, then each side is an exact copy of the other, just left/right being turned.
therefore, yes absolutely, CAD is congruent with CBD. and ACB is congruent to ADB.
but do you notice something ?
both mentioned triangles on the left side contain the side AC, and both triangles in the right side contain the side BD.
now, if the triangles are congruent, that means that each of the 3 sides must have an equally long corresponding side in the other triangle.
therefore, AC must be equal to BD.
and that means that AC is congruent to BD.
because lines have no other congruent criteria - only the lengths must be identical.
The point (-3, -2) is located in which quadrant of the coordinate plane? Just wondering for a study
Answers
Answer:
quadrant 3
negative negative is quadrant 3
Positive negative is quadrant 4
negative positive is 2
Positive positive is 1
Answer:
3rd quadrant
Step-by-step explanation:
because they're both negative
the tetrahedron in the first octant bounded by the coordinate planes and the plane passing through (1, 0, 0), (0, 2, 0), and (0, 0, 3)
Answers
The tetrahedron in the first octant bounded by the coordinate planes and the plane passing through (1, 0, 0), (0, 2, 0), and (0, 0, 3) is passing through (1,2,3).
The general equation of the plane is
ax+by+cz = d
or
x/A + y/B + z/C = 1 where A = d/a, B = d/b, C = d/c
We use the x/A + y/B + z/C = 1 equation to determine the unknowns when, the plan passes through the coordination axis.
The given plane then passes through A (1, 0, 0), B (0, 2, 0), and C. (0, 0,3).
A =1/A + 0/B + 0/C
A = 1
B =0/A + 2/B + 0/C
B = 2
C= 0/A + 0/B + 3/C
C = 3
Thus we can say that the plane is passing through (1,2,3)
A coordinate plane is also known as a rectangular coordinate plane grid, is a two-dimensional plane with a vertical Y-axis and a horizontal X-axis.
To learn more about coordinate plane
brainly.com/question/13854649
#SPJ4
Katelyn wants to build a desk for her doll. Her actual desk is 3 feet tall. The scale is 0.5 in: 1 ft How tall will the doll desk be?
Answers
3ft x 0.5 in per ft = 1.5 inches
In a sample of 1000 U.S. adults, 150 said they are very confident in the nutritional information on restaurant menus. Four U.S adults are selected at random without replacement (a) Find the probability that all four adults are very confident in the nutritional information on restaurant menus (b) Find the probability that none of the four adults are very confident in the nutritional information on restaurant menus 0.522 (c) Find the probability that at least one of the four adults is very confident in the nutritional information on restaurant menus 0.478
Answers
(a)The probability that all four adults are very confident is approximately 0.0056.
(b) The probability that none of the adults are very confident is approximately 0.522.
(c) The probability that at least one adult is very confident is approximately 0.478.
What is the probability of selecting four adults at random without replacement from a sample of 1000 U.S. adults, given the proportion of very confident individuals?
The probability of selecting four adults at random without replacement from a sample of 1000 U.S. adults depends on the proportion of very confident individuals. By calculating the probability of all four adults being very confident (a), none of the four adults being very confident (b), and at least one of the four adults being very confident (c), we can determine the likelihood of these scenarios occurring based on the given information.
To solve this problem, we can use the concept of probability and combinations.
(a)Given that there are 150 out of 1000 U.S. adults who are very confident, the probability of selecting one adult who is very confident is:
P(very confident) = 150/1000
= 0.15
Since the sampling is done without replacement, after each selection, the sample size decreases by 1. Therefore, for the second selection, the probability becomes 149/999, for the third selection, it becomes 148/998, and for the fourth selection, it becomes 147/997.
To find the probability that all four adults are very confident, we multiply these probabilities together:
P(all four adults are very confident) = (0.15) * (149/999) * (148/998) * (147/997)
≈ 0.0056
(b) The probability of selecting one adult who is not very confident (opposite of very confident) is:
P(not very confident) = 1 - P(very confident)
= 1 - 0.15
= 0.85
Since we are selecting four adults at random without replacement, the probability of none of them being very confident can be calculated as:
P(none very confident) = P(not very confident) * P(not very confident) * P(not very confident) * P(not very confident)
= (0.85)* (0.85) * (0.85) * (0.85)
≈ 0.522
(c) The probability of at least one adult being very confident is the complement of none of them being very confident:
P(at least one very confident) = 1 - P(none very confident)
= 1 - 0.522
= 0.478
Therefore,
(a) The probability that all four adults are very confident is approximately 0.0056.
(b) The probability that none of the adults are very confident is approximately 0.522.
(c) The probability that at least one adult is very confident is approximately 0.478.
To learn more about the probability from the given link
brainly.com/question/13604758
#SPJ4
The temperature in a town was 0 °F at 7 a.m. Over the next 312 hours, the temperature rose at a steady rate to 20.3 °F.
What was the temperature at 8 a.m.?
Enter your answer as a decimal in the box.
°F.
Answers
Answer:
5.8
Step-by-step explanation:
First, convert 312 to a decimal:
12=1÷2=0.5
312=3.5
Divide.
20.3÷3.5=5.8
The temperature changed by 5.8 °F every hour. That means the temperature rose from 0 °F to 5.8 °F between 7 a.m. and 8 a.m.
Answer:-3.6
Step-by-step explanation:
if the number of hot lunches sold at school this week was 1,350 and the relative frequency on friday was 0.22, how many lunches were sold on friday?
Answers
296 hot lunches were sold on Friday.
The number of hot lunches sold on Friday can be calculated by multiplying the total number of hot lunches by the relative frequency on Friday:
Hot lunches sold on Friday = 1,350 * 0.22 = 296
What is Relative frequency ?Relative frequency is a measure of the number of times an event occurs in a sample, expressed as a proportion of the total number of events. To find the number of hot lunches sold on Friday, we multiply the total number of hot lunches sold in the week by the relative frequency of Friday. This gives us the number of hot lunches sold on Friday, which is 296 in this case. Understanding relative frequency is important in statistics as it helps to summarize data and understand the distribution of events.
You can learn more about Relative frequency at
https://brainly.com/question/3857836
#SPJ4
What is the cotθ in the right triangle shown?

Answers
f(x) = -4(x+2) what is f(4)
Answers
Answer:
-24
Step-by-step explanation:
f(4)= -4(x+2)
f(4)= -4(6)
f(4)= -24
Answer:
F(x)=-4(x+2)
0=-4-8
4x=-8
X=-2
So,-2×2
-4
Step-by-step explanation:
Have a great day!
the distribution of test scores shows that most students did not do well on the test; some did fine and only a few did exceedingly well. the distribution is likely to be .
Answers
The distribution of test scores shows that most students did not do well on the test; some did fine and only a few did exceedingly well. The distribution is likely to be skewed.
What is a skewed distribution?
A skewed distribution is one in which the data is not uniformly distributed but rather concentrated on one side. In simple words, a skewed distribution is one in which one tail has a greater number of observations than the other tail, with the majority of data falling in the tail with the greater number of observations.
In a symmetric distribution, the data is uniformly distributed on both sides of the median, with half of the data lying to the right and half to the left.
Thus, the distribution of test scores shows that most students did not do well on the test; some did fine and only a few did exceedingly well. The distribution is likely to be skewed.
To know more about skewed distribution: https://brainly.com/question/28315480
#SPJ11
IMAGE BELOW I WIL GIVE BRANLIEST

Answers
Answer:
The scale factor is 2.
Step-by-step explanation:
From the coordiante plane, we can see that:
Point H(4) has been expanded to 4 {4 · 2 = 8}
Point G(1) has been expanded to 2 {1 · 2 = 2}
Point I(-2) has been expanded to -4 {-2 · 2 = -4}
hope this helps!
HELPPPP PLS!! TY
Look at triangle ABC.
Coordinate grid shows negative 5 to positive 5 on the x axis and y axis at intervals of 1. A triangle ABC is shown with A at ordered pair 4, 5, B at ordered pair 1, 2, and C at ordered pair 4, 2.
What is the length of side AB of the triangle? (1 point)
Square root of 6
3
Square root of 18
6
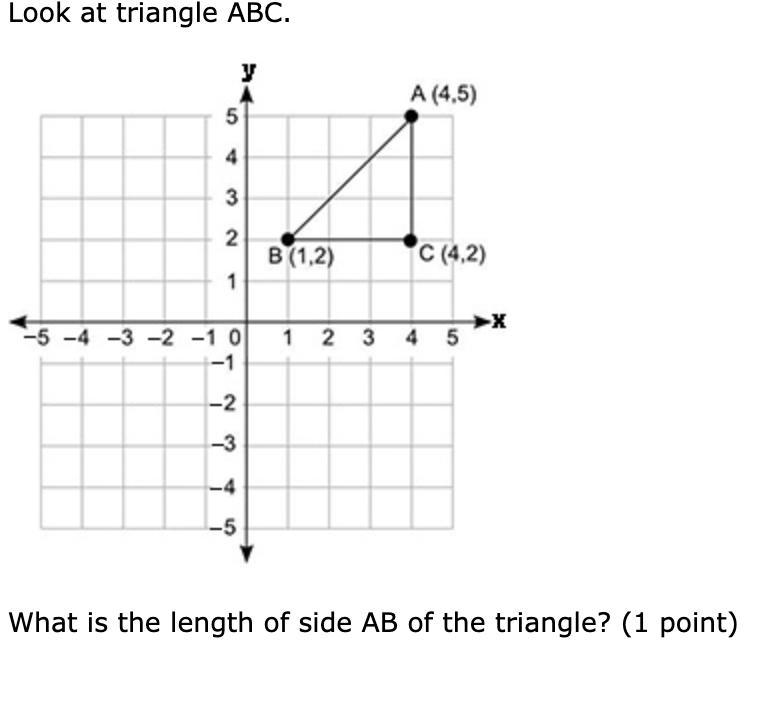
Answers
Step-by-step explanation:
as you can see, the distance between 2 points can always be seen as the Hypotenuse or baseline of a right-angled triangle created by the differences of the x and y coordinates of both points.
the drawn triangle is nothing else than that.
to calculate the length of a side in such a triangle we need to use Pythagoras :
c² = a² + b²
c is the Hypotenuse of baseline of the triangle and is opposite of the 90 degree angle.
a and b are the legs of the triangle "enclosing" the 90 degree angle.
so, we have
AB² = AC² + BC²
AC and BC we know : the coordinate differences in x and y directions.
AC = (4, 5) to (4, 2). as the x coordinates are the same, the difference is just the difference in the y coordinates : 5-2 = 3.
BC = (1, 2) to (4, 2). as the y coordinates are the same, the difference is just the difference in the x coordinates : 5-1 = 3.
AB² = 3² + 3² = 9 + 9 = 18
AB = sqrt(18)
FYI : sqrt(18) = sqrt(9×2) = 3×sqrt(2)
What is √5times√12times√50
Answers
Answer:
Step-by-step explanation:
We can simplify the expression √5 × √12 × √50 as follows:
√5 × √12 × √50 = √(5 × 12 × 50)
To simplify the product under the square root, we can factor the numbers into their prime factors:
5 = 5
12 = 2^2 × 3
50 = 2 × 5^2
Therefore, 5 × 12 × 50 = 2^2 × 3 × 5^3 = 2^2 × 5^3
Substituting this back into the original expression, we get:
√5 × √12 × √50 = √(2^2 × 5^3)
Taking the square root of the product, we can simplify further:
√5 × √12 × √50 = √(2^2) × √(5^3) = 2 × 5√5^2 = 2 × 5 × 5 = 50
Therefore, √5 × √12 × √50 simplifies to 50.
determine the probability that a state is occupied by an electron at (i) 1kt, (ii) 3kt, and (iii) 5kt above the fermi level in a metal
Answers
The probability that a state is occupied by an electron at
i)1kt:0.5
ii) 3kt: 0.7
ii)5kt: 0.9
The probability that a state is occupied by an electron at any given temperature above the Fermi level is calculated using the Fermi-Dirac statistics. This equation states that the probability of a state being occupied is equal to 1/(1+exp(-(E-EF)/KT)), where E is the energy of the state, EF is the Fermi level energy, and KT is the product of Boltzmann's constant and the temperature in Kelvin.
Thus, for a temperature of 1kt above the Fermi level, KT = 1. By plugging these values into the equation, we can calculate that the probability of a state being occupied is 0.5. For a temperature of 3kt and 5kt above the Fermi level, KT = 3 and 5, respectively. Using these values, the probability of a state being occupied at 3kt and 5kt above the Fermi level is 0.7 and 0.9, respectively.
To know more about fermi level refer to the link brainly.com/question/14544528
#SPJ4
Naglakad si Ruben ng 900 sentimetro samantalang si Jaime ay naglakad ng
10 na metro. Gaano kalayo ang pagitan ng nalakad ni Jaime kay Ruben sa
sentimetro?
a. 200 cm c. 300 cm
b. 100 cm d. 250 cm
Answers
Sagot:
100 cm
Hakbang-hakbang na paliwanag:
Kung ganoon :
Distansya na sakop ng Ruben = 900 centimetri
Distansya na sakop ng Jamie = 10 metro
Pagko-convert sa centimeter:
100 cm = 1 m
x cm = 10 m
Paggamit ng multiplikasyon ng krus:
x = 100 * 10
x = 1000 cm.
Dahil dito Distansya ni Jamie = 1000 cm
Distansya sa pagitan ng Jamie at Ruben;
1000 cm - 900 cm = 100 cm
kite EFGH is graphed on the coordinate plane. three of its verticies are E(1,6), F(3,5), and G(4,-3). what are the coordinates of the fourth vertex, H?
Answers
The coordinates of the fourth vertex, H is; (-6.056, 7.302)
How to find the Coordinates of a Kite?
A kite has 4 sides and we know that a pair of diagonally opposite angles of a kite are said to be congruent.
We are given the coordinates of its' vertices as;
E(1,6), F(3,5), and G(4,-3).
The two diagonals are perpendicular;
Slope of EG = (-3 - 6)/(4 - 1)
Slope of EG = -9/5
Equation of line passing through G is;
y = mx + c
-3 = -9/5(4) + c
-15 = -36 + 15c
c = 51/15 = 17/5
y = (-9/5)x + 17/5 ------(1)
Equation of line passing through F is;
y = mx + c
6 = (5/9)(1) + c
54 = -9 + 9c
c = 7
y = (5/9)x + 7 -----(2)
Solving eq 1 and eq 2 simultaneously gives;
x = -1.528 and y = 6.151
If (a, b) are coordinates of vertex H, then;
(a + 3)/2 = -1.528 and (b + 5)/2 = 6.151
Thus;
a = -6.056 and b = 7.302
Read more about Kites coordinates at; https://brainly.com/question/27761176
#SPJ1
The probability of a New York teenager owning a skateboard is 0.37, of owning a bicycle is 0.81 and of owning both is 0.36. If a New York teenager is chosen at random, what is the probability that the teenager owns a skateboard or a bicycle
Answers
According to the question The probability that a New York teenager owns a skateboard or a bicycle is 0.82.
Let's denote the event of owning a skateboard as \(\(A\)\) and the event of owning a bicycle as \(\(B\).\)
We are given:
\(\(P(A) = 0.37\)\) (probability of owning a skateboard)
\(\(P(B) = 0.81\)\) (probability of owning a bicycle)
\(\(P(A \cap B) = 0.36\)\) (probability of owning both skateboard and bicycle)
To find the probability that the teenager owns a skateboard or a bicycle \((\(A \cup B\))\) , we can use the formula:
\(\[P(A \cup B) = P(A) + P(B) - P(A \cap B)\]\)
Substituting the given values:
\(\[P(A \cup B) = 0.37 + 0.81 - 0.36\]\)
Calculating:
\(\[P(A \cup B) = 0.82\]\)
Therefore, the probability that a New York teenager owns a skateboard or a bicycle is 0.82.
To know more about probability visit-
brainly.com/question/29286790
#SPJ11
In a typical month, the BBC Corporation receives 30 checks totaling $250,000. These are delayed five (5) days on average What is the average daily float? Assume 30 days per month. 0 $1,250,000 0 $1,500,000 O $41,667
Answers
The average daily float for the BBC Corporation, based on receiving 30 checks totaling $250,000 with an average delay of five days, is $41,667.
To calculate the average daily float, we need to determine the total amount of funds in transit and divide it by the average number of days the funds are delayed.
In this case, the BBC Corporation receives 30 checks totaling $250,000 in a typical month. The average delay for these checks is five days.
To calculate the total amount of funds in transit, we multiply the average daily amount by the average delay:
Total funds in transit = Average daily amount × Average delay
= ($250,000 / 30 days) × 5 days
= $8,333.33 × 5
= $41,666.67
Rounding to the nearest whole number, the average daily float is $41,667.
Learn more about funds here:
https://brainly.com/question/20383417
#SPJ11
The first approximation of 537 can be written a b' where the greatest common divisor of a and bis 1, with a= type your answer... b = = type your answer...
Answers
The first approximation of 537 can be written as a = 536 and b = 1, where the greatest common divisor of a and b is 1.
In number theory, the greatest common divisor (GCD) of two numbers is the largest positive integer that divides both numbers without leaving a remainder. In this case, since a = 536 and b = 1, the GCD of a and b is 1. This means that 536 and 1 have no common factors other than 1.
The first approximation of 537 can be expressed as a product of these two numbers, a and b, where a represents the larger part of the approximation and b represents the smaller part. In this case, a is equal to 536, and b is equal to 1. Since the GCD of a and b is 1, it indicates that 536 and 1 have no common factors other than 1. This approximation may not be the most accurate, but it satisfies the condition of having a GCD of 1.
Learn more about greatest common divisor :
https://brainly.com/question/23270841
#SPJ11
