Perimeter < 18.7 feet
4,1 ft
4.9 ft/
6.4 ft
x ft
Inequality:
Solution:

The null hypothesis in a one-way ANOVA test is that there is no treatment effect. This means that the mean scores of the groups being compared are not significantly different. The one-way ANOVA test is a statistical method used to compare the means of three or more groups.

The one-way ANOVA test requires that certain assumptions be met, including that the data is normally distributed and that the variances of the groups being compared are equal. If these assumptions are met, then the test can be used to determine whether there is a significant difference between the means of the groups. The test works by comparing the variability between the groups to the variability within the groups.

If the variability between the groups is larger than the variability within the groups, then it is likely that there is a significant difference between the means of the groups. The alternative hypothesis in a one-way ANOVA test is that there is some treatment effect, which means that at least one of the group means is different from the others.

If the null hypothesis is rejected, then the alternative hypothesis is accepted, and it can be concluded that there is a significant difference between the means of the groups. The one-way ANOVA test is useful for determining whether there is a significant difference between the means of several groups, but it does not provide information about which specific group means are different. To determine which group means are different, post hoc tests can be performed.

To know more about statistical visit:

https://brainly.com/question/31538429

#SPJ11

Answer:

1. 24  2. 65  3. 6.5

Step-by-step explanation:

1. You break it in half and do the algortim bxh/2 . First would be 4x2/2 is 4 and 4x10/2 is 20. Add them and you get 24.

2. This would have 3 parts, 2 triangles and 1 square. the square would be 6x5 which is 30. the 2 triangles will be the same area so to find out what to divide 5 by, you would do 13-6= 7. 7x5=35 which will equal both triangles. 30+35=65

3.  bxh/2  so 4x3.25 is 13 and that /2 is 6.5

Answer: (0, 0), (0, 1), (1, 2), (1, 3) does NOT represent a function

Step-by-step explanation:

to tell whether a set of ordered pairs are functions or not, all domains must have different ranges!

range: x-axis (0,0)

domain: y-axis (0,0)

pair 1:

all the ranges - 0, 1, 2, 3 - are different, which means it IS a set of ordered pairs

pair 2:

all the ranges - 0, 0, 1, 1 - are NOT all different, which means it is NOT a set of ordered pairs

pair 3:

all the ranges - 1, 2, 3, 4 - are different, which means it IS a set of ordered pairs

pair 4:

all the ranges - 0, 1, 2, 3 - are different, which means it IS a set of ordered pairs

let me know if you have any more questions or if i made any mistakes. hope this helped, and good luck! ˶ˆ꒳ˆ˵

Answer:

I'd say the first and third options would be correct.

Step-by-step explanation:

Answer:

Below

Step-by-step explanation:

If it is a fair spinner then

First option is true

second option is true

third option cannot be determined from info given  

4th option is true

Answer:

A. corresponding

Step-by-step explanation:

Corresponding angles are angles that lie on top of two parallel lines.

Alternate interior angles are angles that lie on two sides of parallel lines and are mostly located with one angle up and one angle down.

Same side interior angles are angles within two parallel lines.

Answer:

corresponding angles

Step-by-step explanation:

∠ 2 and ∠ 6 are corresponding angles because each is in the same position ( upper right- hand corner ) in its group of 4 angles.

Answer:

Step-by-step explanation:

Maureen spent $152 on CDs and DVDs. She spent $56 on the CDs and the rest on DVDs. If she bought 6 DVDs for the same price each, how much did Maureen spend on each DVD?

Answer:

See below.

Step-by-step explanation:

Model the system of equations, and solve for x to determine the required horizontal distance.

\(\left \{ {{y=-0.5x^2+3x+10} \atop {y=-0.2+7}} \right.\)

Transform the quadratic equation into standard form and substitute for y into linear equation. Since the quadratic equation already is in the standard form, substitute for y:

\(y=-0.2x+7\)  ---> Rewrite the linear equation.

\(-0.5x^2+3x+10=-0.2x+7\) ---> Substitute \(y=-0.5x^2+3x+10\).

\(-0.5x^2+3.2x+3=0\) ----> Simplify.

Solve the equation by using the Quadratic Formula:
Identify \(a=-0.5,b=3.2,c=3.\)

\(x=\frac{-b\pm\sqrt{b^2-4ac} }{2a}\)         -----------------> Write the Quadratic Formula.

\(=\frac{-3.2\pm\sqrt{3.2^2-4*(-0.5)*3} }{2*(-0.5)}\) -------------------> Substitute for a, b, and c.

\(=\frac{-3.2\pm\sqrt{16.24} }{-1}\) ----------------------> Simplify.

\(=3.2\pm4.03\) --------------------> \(\sqrt{16.24}=(\text{Estimated})4.03\) and simplify.

\(x=7.23\), and

\(x = -0.83\)

The distance does not make sense for negative numbers, so only consider \(x=7.23.\)

Thank you,

Eddie Echevarria

The volume of the solid bounded by the graph of y = sin(x), y = 0, x = 0, and x = π, where the cross-sections are equilateral triangles perpendicular to the x-axis, is approximately 1.633 cubic units.

What is volume of solid?

The volume of a solid refers to the amount of three-dimensional space enclosed or occupied by the solid object.

To find the volume of the solid, we integrate the area of the equilateral triangles as they vary along the x-axis.

The base of each equilateral triangle is the width of the region, which is given by the difference in x-coordinates between x = 0 and x = π, so the base length is π - 0 = π units.

The height of each equilateral triangle is the distance between the y-coordinate of the graph y = sin(x) and y = 0. Since the graph y = sin(x) oscillates between -1 and 1, the height is 1 - 0 = 1 unit.

The area of an equilateral triangle can be calculated using the formula A = (sqrt(3)/4) * s², where s is the length of one side.

Therefore, the volume can be calculated by integrating the area function over the interval [0, π]:

V = ∫[0,π] (sqrt(3)/4) * (π)² dx

Evaluating this integral yields V ≈ 1.633 cubic units.

learn more about Volume of solid here:

https://brainly.com/question/24327362

#SPJ4

Answer:

14

Step-by-step explanation:

If Bob has 22 pints, and one glass is one pint, the 22-8 = 14

Answer:

14

Step-by-step explanation:

you would subtract 8 pints of soda left from the total pints which is 22 to get 14 pints used during the party

22-8=14

Rounding to the nearest integer, we have E[X200|X100 = 70] ≈ 92 for the urn.

The expected number of red balls in the urn after another 100 draws, denoted by E[X200|X100 = 70], can be found using the formula:

E[X200|X100 = 70] = E[Y200|Y100 = 35/51] * (200 + 2) - 2

where Yn = Xn/(n + 2).

Since Yn is a random variable, we need to find its expected value at time 200 given that it was 35/51 at time 100. Using the fact that Yn = Xn/(n + 2), we have:

E[Y200|Y100 = 35/51] = E[X200/(200 + 2)|X100/(100 + 2) = 35/51]
= (200/102) * E[X200|X100 = 70]

where we used the fact that E[aX] = aE[X] for any constant a.

Now, since we know X100 = 70, we can use the fact that Xn follows a binomial distribution with parameters n and p, where n is the number of draws and p is the probability of drawing a red ball. At time 100, we have made 100 draws and obtained 70 red balls, so the probability of drawing a red ball at time 100 is p = 70/100 = 7/10. Therefore, we have:

E[X200|X100 = 70] = E[X200/(200 + 2)|X100/(100 + 2) = 35/51]
= (200/102) * E[X200|X100 = 70]
= (200/102) * (100 + 2) * (7/10)
= 92

Rounding to the nearest integer, we have E[X200|X100 = 70] ≈ 92.

Learn more about urn here:

https://brainly.com/question/30666719

#SPJ11

The solution to the given problem of the triangle comes out to be AC are 20 units long.

If a polygon contains at least one more segment, it is a hexagon. It is a simple rectangle in shape. Anything identical to a standard triangle form can only be distinguished from it by edges across A and B. Euclidean geometry does not completely describe the cube, despite the fact that its edges are all collinear. A triangle is formed by a circle with five sides and three angles.

Here,

If DE is the midpoint of triangle ABC, DE is parallel to AC and has a length of 50% of AC.

Let's use "x" units to represent the length of AC.

Given the information, DE equals 10 units, or 50 percent of AC's length. So that we may create the equation:

=>  DE = AC/2

When we enter DE's value as 10 units, we get:

=> 10 = x/2

To separate x, we multiply both sides of the equation by 2 and obtain:

=> 2 * 10 = x

=> x = 20

Therefore, AC is 20 units long.

To know more about triangles visit:

brainly.com/question/2773823

#SPJ1

Answer:

£120

Step-by-step explanation:

With regards to the above, the difference between the ratio is

3:1 is 2

I.e

(3 - 1) = 2

Nick gets 2 extra, which is equal to £60

Therefore,

1 share = £60/2 = £30

June gets 1 share = 1 × £30 = £30

Nick would get = 3 × £30 = £90

Therefore, the value gotten by both would be;

= £30 + £90

= £120

Answer:

answer down below <3

Step-by-step explanation:

Answer:

122.

Step-by-step explanation:

nthe term = a1 + d(n - 1) so here:

20th term = -30 + 8(20 - 1)

- 30 +  152

= 122.

Answer:

D

Step-by-step explanation:

Somehting bknbye3uehnfhnjun Español uno, como sulfhídrica

In the context of engineering and construction, a bearing point refers to a specific location or area. The bearing of A from C is 230°.

The load from the structural element is transferred to the foundation at a bearing point, which is often a concentrated load point.

To avoid structural failure, settling, or excessive deflection of the part, it is crucial to make sure the bearing point is properly designed and supported.

Since the bearing of C from A is 050°, we can find the bearing of A from C by adding 180° to 50°, which gives us:

Bearing of A from C = 50° + 180° = 230°

Therefore, In the context of engineering and construction, a bearing point refers to a specific location or area. The bearing of A from C is 230°.

Learn more about bearing here:

brainly.com/question/15006070

#SPJ1

Complete question -

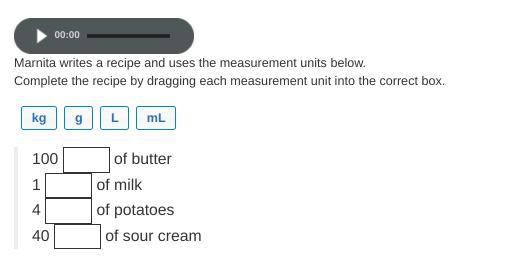
Answer:

Step-by-step explanation:

100 G

1 L

4 Kg

40 ML

Answer:

100 ml's of butter 1 g of milk 4 l of potatoes and 40 kg's of sour cream

Step-by-step explanation:

pls mark me brainlyest!

The source of error variance that does not affect test-retest reliability but would affect the reliability of a parallel forms test is called time sampling error.

Error variance is a term used to describe the variability in test scores that is not caused by the trait or ability being measured. Test-retest reliability is a measure of consistency over time. This type of reliability can be determined by measuring the same trait or ability in the same group of people on two separate occasions. If the measure is reliable, then the scores on the first and second occasions should be similar. Parallel forms reliability is a measure of consistency between two different tests that are designed to measure the same trait or ability. If the two tests are highly correlated, then they can be considered to be parallel forms. Error variance due to time sampling refers to the variability in test scores that is caused by the fact that people's scores can vary from one test administration to the next due to factors that are unrelated to the trait or ability being measured. Since this type of error is related to the passage of time, it would have an effect on the reliability of a parallel forms test but not on the reliability of a test-retest.

Learn more about test-retest reliability:

brainly.com/question/13860893

#SPJ11

If you invest $3,750 at the end of each of the next six years at an interest rate of 1.9% per annum, you will have approximately $23,596 after 6 years.

To calculate the total amount accumulated after 6 years, we can use the formula for the future value of an ordinary annuity. The formula is given as:

Future Value = Payment * [(1 + Interest Rate)^n - 1] / Interest Rate

Here, the payment is $3,750, the interest rate is 1.9% per annum (or 0.019 as a decimal), and the number of periods (years) is 6.

Substituting the values into the formula:

Future Value = $3,750 * [(1 + 0.019)^6 - 1] / 0.019

= $3,750 * (1.019^6 - 1) / 0.019

≈ $23,596

Therefore, after 6 years of investing $3,750 at the end of each year with a 1.9% interest rate per annum, you would have approximately $23,596. Hence, the correct answer is $23,596.

Learn more about interest rate here:

https://brainly.com/question/27743950

#SPJ11

The centroid of the region bounded by f and g is \((\bar x, \bar y) = (\frac{(m+1)(n+1)}{(m+2)(n+2)}, \frac{(m+1)(n+1)}{(2m + 1)(2n + 1)})\)

From the question, we have the following parameters that can be used in our computation:

\(f(x) = x^n\) and \(g(x) = x^m\)

Also, we have the interval to be [0, 1]

Assuming the region is of uniform density, compute the mass of the region and its moments.

If n > m, then in the interval [0, 1] we have f(x) ≤ g(x).

This means the mass is

\(M = \int\limits^1_0 {(g(x) - f(x))} \, dx\)

So, we have

\(M = {[\dfrac{x^{m+1}}{m+1} - \dfrac{x^{n+1}}{n+1}]} |\limits^1_0\)

When expanded, we have

\(M = \dfrac{1}{m + 1} - \dfrac{1}{n + 1}\)

So, the moments are

\(M_x = \int\limits^1_0 {\frac{g(x)^2 - f(x)^2}{2} \, dx\)

\(M_x = \frac{1}{2}(\frac{x^{2m +1}}{2m + 1} - \frac{x^{2n +1}}{2n + 1} )|\limits^1_0\)

\(M_x = \dfrac{1}{2}(\frac{1}{2m + 1}- \frac{1}{2n + 1})\)

\(M_y = \int\limits^1_0 {x(g(x) - f(x)) \, dx\)

\(M_y = \int\limits^1_0 {x^{m+1} - x^{n+1} \, dx\)

\(M_y = (\frac{x^{m + 2}}{m + 2} - \frac{x^{n + 2}}{n + 2} )|\limits^1_0\)

\(M_y = \frac{1}{m + 2}- \frac{1}{n + 2}\)

So, the centroid is

\((\bar x, \bar y) = (\frac{M_y}{M}, \frac{M_x}{M})\)

This gives

\((\bar x, \bar y) = (\frac{(m+1)(n+1)}{(m+2)(n+2)}, \frac{(m+1)(n+1)}{(2m + 1)(2n + 1)})\)

Hence, the centroid is \((\bar x, \bar y) = (\frac{(m+1)(n+1)}{(m+2)(n+2)}, \frac{(m+1)(n+1)}{(2m + 1)(2n + 1)})\)

Read more about centroid at

https://brainly.com/question/7644338

#SPJ1

Question

Consider the given functions \(f(x) = x^n\) and \(g(x) = x^m\) on the interval [0, 1], where m and n are positive integers and n > m.

Find the centroid of the region bounded by f and g.

Answer:

35

Step-by-step explanation:

3:5

21;35

as it must be * by 7 as 3*7=21

so therefore we times 5*7 as well

so they has 35 loses

Answer:

0.9 cm

Step-by-step explanation:

c is the length of the side. a is the altitude. b is the base. a is the vertical bisector if the base, so the base is 0.5 cm.

c² = a² + b²

1² = a² + 0.5²

1² - 0.5² = a²

1 - 0.25 = a²

√0.75 = a

0.8660254 = a

round to 0.9

Answer:

x = -3    b no answer is 1/27000

Step-by-step explanation:

Answer:

Step-by-step explanation:

Elysa would have to save money for 6 weeks to afford the glove

46.50-15= 31.5/5.25= 6

Answer:

Your answer is: - x - 2

Simplify the expression.

Step-by-step explanation:

Hope this helped : )

9514 1404 393

Answer:

  c = -3; d = 5

Step-by-step explanation:

The function is differentiable if it is continuous and the derivative is continuous.

This function will be continuous if the limit as x approaches 3 from either side is the same. From the left, the limit is ...

  5(3^2) +c = 45 +c

From the right, the limit is ...

  d(3^2) -3 = 9d -3

__

The derivative will be continuous if the limit as x approaches 3 from either side is the same. From the left, the limit is ...

  f'(x) = 10x

  = 10(3) = 30

From the right, the limit is ...

  f'(x) = 2dx

  = 2d(3) = 6d

__

This gives us a pair of simultaneous equations in 'c' and 'd':

  45 +c = 9d -3

  6d = 30

The latter tells us d = 5. Then the former tells us ...

  45 +c = 9(5) -3   ⇒   c = -3

The function is differentiable if c = -3 and d = 5.

_____

Additional comment

With these values, the function becomes ...

  \(f(x)=\begin{cases}5x^2-3&\text{if }x\le 3\\5x^2-3&\text{if }x>3\end{cases}\)

The function f(x) is given by f(x) = 4x^(3/2) + 2x^(5/2) + 3, where f'(x) = √x (6 + 5x) and f(1) = 9.

To find f(x), we need to integrate f'(x) with respect to x. Using the power rule of integration, we can integrate the square root of x multiplied by (6 + 5x) as follows:

f(x) = ∫√x (6 + 5x) dx
     = ∫(6x^1/2 + 5x^3/2) dx
     = 4x^(3/2) + 10/5 x^(5/2) + C

where C is the constant of integration.

To find C, we can use the given value of f(1) = 9. Substituting x = 1 in the above equation, we get:

f(1) = 4(1)^(3/2) + 10/5 (1)^(5/2) + C
     = 4 + 2 + C
     = 6 + C

Therefore, C = f(1) - 6 = 9 - 6 = 3.

Substituting this value of C in the equation for f(x), we get:

f(x) = 4x^(3/2) + 2x^(5/2) + 3

So, the function f(x) is given by f(x) = 4x^(3/2) + 2x^(5/2) + 3, where f'(x) = √x (6 + 5x) and f(1) = 9.

To learn more about f(x) visit :

https://brainly.com/question/30171899

#SPJ11

The forecast for the next period using the following weights: 0.3, 2, 0.5 is Option d. 421.

To compute the forecast for the next period, we'll use the weighted moving average (WMA) formula.WMA formula:

WMA = W1Yt-1 + W2Yt-2 + ... + WnYt-n

Where, WMA is the weighted moving average

W1, W2, ..., Wn are the weights (must sum to 1)

Yt-n is the demand in the n-th period before the current period

As we know Month 1 – 381, Month 2-366, and Month 3 - 348.

Weights: 0.3, 2, 0.5

We'll compute the forecast for the next period (month 4) using the data:

WMA = W1Yt-1 + W2Yt-2 + W3Yt-3WMA

= 0.3(381) + 2(366) + 0.5(348)WMA

= 114.3 + 732 + 174WMA

= 1020.3

Therefore, the forecast for the next period is 1020.3, which rounds to 421. Hence, option d is correct.

You can learn more about forecasts at: brainly.com/question/30167588

#SPJ11

Answer:

0.5 or 5/10

Step-by-step explanation:

Answer:

Equivalent Fractions for 6/12: There are infinity equivalent fractions to 612. See some examples: 12, 24, 36, 48, 510, 612, 714, 816, 918, 1020, 1122, 1224, 1326, 1428, 1530, 1632, 1734, 1836, 1938, 2040...

Step-by-step explanation:

i hope it's help you