Passing through (3,3) and parallel to the line whose equation is 2x+y-2=0; slope intercept form.
Answers
Answer:
Step-by-step explanation:
y = -2x +2
y - 3 = -2(x -3)
y - 3 = -2x + 6
y = -2x + 9
Related Questions
the total cost of a watch and a radio is rs 500 .If the watch is cheaper than the radio by rs 150,find their cost
Answers
Let cost of watch=r
w+r=500
but w=r-150
So;r-150+r=500
2r=500+150
2r=650
r=650/2
r=325
If r=325,
then w+r=500
w+325=500
w=500-325
w=175
Cost of watch=rs175
Cost of radio=rs325
calls for dial-in connections to a computer center arrive at an average rate of four per minute. the calls follow a poisson distribution. if a call arrives at the beginning of a one-minute interval, what is the probability that a second call will not arrive in the next 20 seconds?
Answers
The probability that a second call will not arrive in the next 20 seconds is approximately 0.2636 or 26.36%.
What is Poisson probability?Poisson probability is a mathematical concept that describes the probability of a certain number of events occurring in a fixed interval of time or space, given a known average rate of occurrence. The Poisson probability distribution is named after French mathematician Siméon Denis Poisson, who introduced it in the early 19th century to model the occurrence of rare events, such as errors in counting or measurement, accidents, or phone calls.
The Poisson probability distribution is a discrete probability distribution that gives the probability of a certain number of events (x) occurring in a fixed interval (t), when the average rate of occurrence (λ) is known. The Poisson probability distribution assumes that the events occur independently and at a constant average rate over time or space. The formula for Poisson probability is:
P(x; λ) = (\(e^{-\lambda}\)) * λˣ) / x!
where:
P(x; λ) = the probability of x occurrences in a given interval, when the average rate is λ
e = a mathematical constant e (approximately 2.71828)
λ = it is the average rate of occurrence in the given interval
x = it is number of occurrences in the given interval
Given that calls for dial-in connections arrive at an average rate of four per minute and follow a Poisson distribution, we can use the Poisson probability formula to solve this problem. The Poisson probability formula is:
P(x; λ) = (\(e^{-\lambda}\)) * λˣ) / x!
where:
P(x; λ) = the probability of x occurrences in a given interval, when the average rate is λ
e = a mathematical constant e (approximately 2.71828)
λ = the average rate of occurrence in the given interval
x = it is the number of occurrences in the given interval
In this problem, we are interested in finding the probability that a second call will not arrive in the next 20 seconds, given that a call has already arrived at the beginning of a one-minute interval. Since we are given the average rate of calls per minute, we need to adjust the interval to 20 seconds, which is 1/3 of a minute. Therefore, the average rate of calls per 20 seconds is:
λ = (4 calls/minute) * (1/3 minute) = 4/3 calls/20 seconds
Using the Poisson probability formula, we can calculate the probability of no calls arriving in the next 20 seconds:
P(0; 4/3) = ( \(e^{-4/3}\)* (4/3)⁰) / 0! = \(e^{-4/3}\) ≈ 0.2636
To know more about probability, visit:
https://brainly.com/question/30034780
#SPJ1
56,234,567, as a single digit times a power of ten
Answers
Answer:
5.6235567 * \(10^{7}\) as scientific notation
A single digit times a power of ten is called a scientific notation.
If my answer helped, kindly mark me as the brainliest!!
Thank You!!
5.6234567 x 10 to the seventh power (10*7)
Explanation:
by using scientific notation you move the decimal point to the left 7 times which makes it a single digit and the exponent to ten as 7
help me on this question!! new here!!

Answers
The constant of proportionality for Tables 1,2,3,4,5 and 6 are 7, 3, 0.25, 14, 5/12 and 7/30 respectively
How to calculate the constant of proportionality?What is constant of proportionality?
The constant of proportionality is the constant value of the ratio between two proportional quantities.
In this case, the constant of proportionality (k) is the ratio of y and x
i.e. k = y/x
To complete the table:
Note: k = y/x, y = kx and x = y/k
Table1:
x | 3 | 7 | 8 | 10 |
y | 21 | 49 | 56 | 70 |
constant of proportionality = 21/3 = 7
Table 2:
x | 4 | 24 | 15 | 3 |
y | 12 | 8 | 45 | 9 |
constant of proportionality = 24/8 = 3
Table 3:
x | 12 | 36 | 8 | 48 |
y | 3 | 9 | 2 | 12 |
constant of proportionality = 12/48 = 0.25
Table 4:
x | 7 | 11 | 5 | 2 |
y | 98 | 154 | 70 | 28 |
constant of proportionality = 70/5 = 14
Table 5:
x | 24 | 12 | 36 | 108 |
y | 10 | 5 | 15 | 45 |
constant of proportionality = 5/12
Table 6:
x | 60 | 1 | 0 | 30 |
y | 14 | 7/30 | 0 | 7 |
constant of proportionality = 7/30
Therefore, the corresponding values of the constant of proportionality for Tables 1, 2, 3, 4, 5 and 6 are 7, 3, 0.25, 14, 5/12 and 7/30
Learn more about constant of proportionality on:
brainly.com/question/1835116
#SPJ1
16. Find the area of the sector.

Answers
The area of the sector with a central angle of 60 degree and radius of 8 units is approximately 33.5 sqaure units.
What is the area of the sector?A sector of a circle is simply part of a circle made up of an arc and two radii.
The area of a sector of a circle can be expressed as:
Area = (θ/360º) × πr²
Where θ is the sector angle in degrees, and r is the radius of the circle.
From the image:
Measure of central angle θ = 60 degrees
Radius r = 8 units
Plug these values into the above formula and solve for the area:
Area = (θ/360º) × πr²
Area = (60°/360°) × π × 8²
Area = 1/6 × π × 64
Area = 1/6 × π × 64
Area = 33.5 sqaure units.
Therefore, the area is approximately 33.5 sqaure units.
Learn more about area of sector here: brainly.com/question/7512468
#SPJ1
Find the exact length of the third side?

Answers
Answer:
57 for the third side
Step-by-step explanation:
a = √(c² - b²)
I need please it would really help me alot !!
no link or zooms
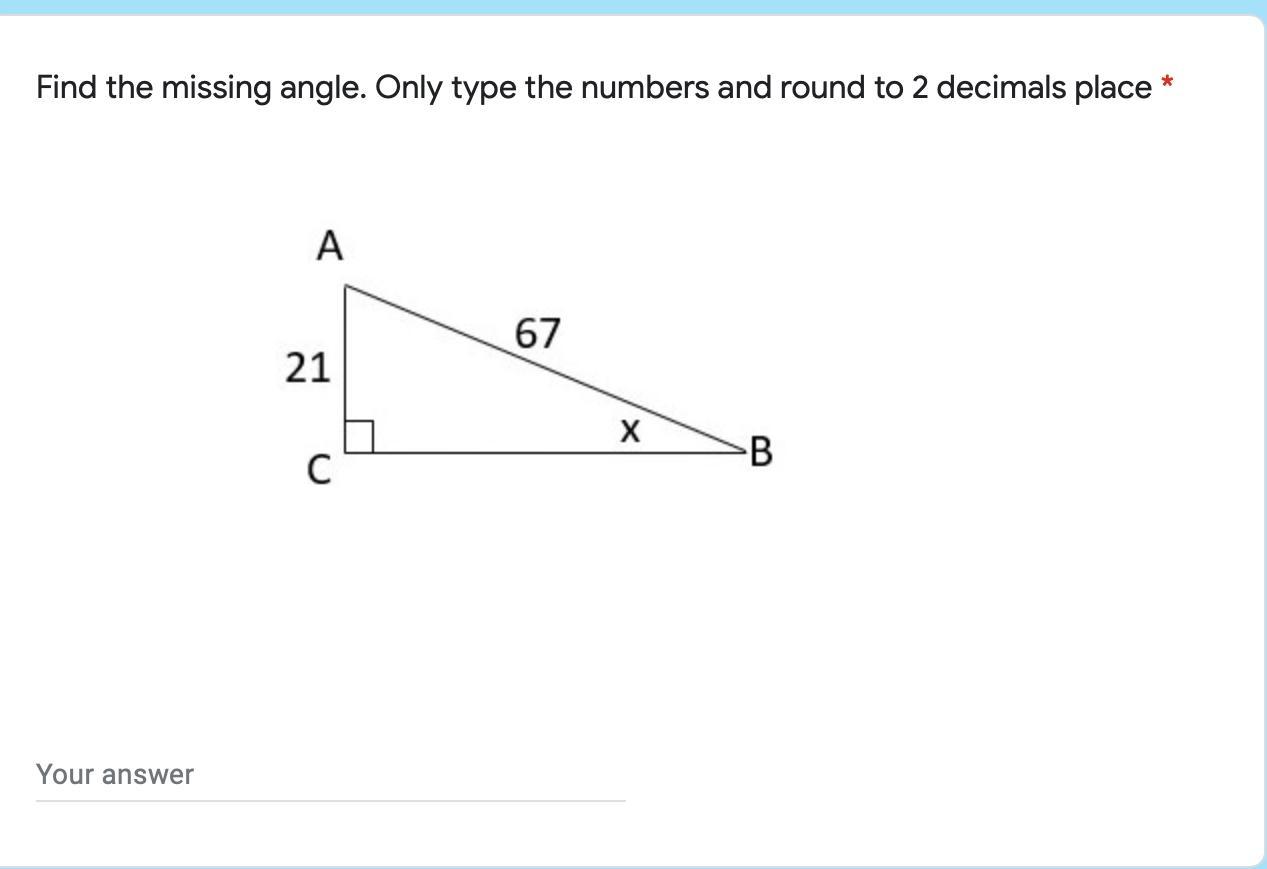
Answers
Answer:
18.266
Step-by-step explanation:
The linear mapping x > Ux preserves lengths and orthogonality. Which of the following equalities is/are true about this statement? I. (UX){Uy)=x.y
II. (Ux).(Uy)=x.y
III. (Ux).(Uy)=0x.y=0
(a) I only
(b) II and III only
(c) I and II only
(d) I and III only
Answers
The correct answer is (c) I and II only.
Given that the linear mapping U preserves lengths and orthogonality, we can determine the correct equalities.
I. (Ux) · (Uy) = x · y
This equality is true because preserving orthogonality means that the dot product of Ux and Uy is equal to the dot product of x and y.
II. (Ux) · (Uy) = x · y
This equality is also true because preserving lengths means that the dot product of Ux and Uy is equal to the dot product of x and y.
III. (Ux) · (Uy) = 0 · x · y = 0
This equality is not necessarily true. It states that the dot product of Ux and Uy is always zero, which is not necessarily the case. The preservation of lengths and orthogonality does not guarantee that the dot product will always be zero.
Therefore, the correct answer is (c) I and II only.
Learn more about linear here:
https://brainly.com/question/31510526
#SPJ11
Please help! Read the question below:

Answers
The equation that represents the graph of function g is: g(x) = 3f(x).
What is the Graph of a Linear Function?A linear function is often expressed as y = mx + b (slope-intercept form), where the slope of the function is the value of "m", while the y-intercept, which is the point where the line cuts the y-axis is the value of "b".
To find the linear function equation for the graph of g, find the slope (m) and determine the point on the y-axis where the line intercepts it, b.
Slope of function g (m) = rise/run = 3/1
Slope of function g (m) = rise/run = 3
The graph of the function of g intersects the y-axis at 0. b = 0
The slope of function .f = 1. This means the slope of function g is three times the slope of the function of .f.
Therefore, the best representation for the graph of function g is: g(x) = 3f(x).
Learn more about function graph on:
https://brainly.com/question/4025726
#SPJ1
Find the area of the region that lies above the x-axis, below the curve x=t^2+7t+8,y=e−tx=t^2+7t+8,y=e-t with 0≤t≤10≤t≤1. Give your answer exactly or round to four decimal places.
Answers
The area of the region that lies above the x-axis, below the curve \(x=t^2+7t+8\), y=e^-t with 0≤t≤1 is approximately 2.1185 square units.
To find the area of the region bounded by the x-axis and the curve, we need to integrate the curve between the limits of t=0 and t=1.
∫₀¹ \(e^-t dt = [-e] ^{-t}\)from 0 to 1 = 1 - 1/e
So, the equation of the curve intersects the x-axis when y=0. To find the x-coordinate of the intersection point, we set y=0 in the equation of the curve:
\(0=e^-t\)
t=0
Thus, the intersection point is (8,0). We also need to find the value of t for which the curve is at its lowest point. To find the minimum point of the curve, we take the derivative of the equation of the curve and set it equal to zero.
y' = \(-e^{-t(2t+7)}\)
0 = \(-e^{-t(2t+7)}\)
t = -7/2
Since t is bounded by 0 and 1, the minimum point of the curve lies within the given range of t. Therefore, the area of the region bounded by the x-axis and the curve is given by the definite integral:
∫₀¹\((t^2+7t+8) e^{-t} dt\)
This integral can be evaluated using integration by parts. After integrating, differentiating, and simplifying, we get:
∫₀¹\((t^2+7t+8) e^{-t} dt\) = 2.1185 (rounded to four decimal places).
Therefore, the area of the region that lies above the x-axis, below the curve\(x=t^2+7t+8\), \(y=e^-t\) with 0≤t≤1 is approximately 2.1185 square units.
Learn more about equation of the curve here: https://brainly.com/question/31467851
#SPJ11
12 feet
8 feet
6.5 feet
Door
3 foet
Mrs. Foster is planning to wallpaper one walt of her game room, shown
above. How much wallpaper will she need?
2.

Answers
Answer:
96sq ft. u just multiple the length by the height then square it
The Punnett square shows the possible genotype combinations of two parents who are homozygous for a trait.
What is the probability of the parents having a child that is heterozygous for this trait?
Group of answer choices
44. 75%
3. 25%
2. 0%
1. 100%

Answers
Heterozygous refers to a pair of alleles in which one is dominant and one is recessive. As you can see, all genotypes for possible offspring in the Punnett square are heterozygous. This means the probability of the parents having a child that is heterozygous is 100 percent likely.
Answer: 100%
A real estate agent sold a lot for P550,000.00. If his agency pays 10% commission, how much commission will he/she receive?
Answers
Answer:
P55,000
Step-by-step explanation:
The amount of commission is found by multiplying the commission rate by the value of the sale(s).
commission = rate × sales
commission = 0.10 × p550,000 = P55,000
The agent will receive P55,000 in commission.
_____
Check
The amount of commission cannot be more than the value of the sale. It is generally a small fraction of the sale value. Here, it is 1/10.
can you help me please
Answers
Find the sum of each infinite geo sequence

Answers
Answer:
0.15 repeating
Step-by-step explanation:
Zorah, a musician, pays $120 to have her instrument tuned and $10 per hour for a booth at a fair. She estimates that she earns$25 per hour in tips. The equation can be used to represent the break even point.
Answers
Answer:
To break-even, Zorah needs to play for 8 hours.
Step-by-step explanation:
To calculate the break-even point in hours, we need to use the following formula:
Break-even point in units= fixed costs/ contribution margin per unit
Break-even point in units= 120 / (25 - 10)
Break-even point in units= 8 hours
To break-even, Zorah needs to play for 8 hours.
A particular satellite is 10 ft wide. A
model of it was built with a scale of 1 in :
2 ft. How wide is the model?
Answers
3 ft
Step-by-step explanation:
The probability that a household owns a pet is 0. 55. Suppose there are 5 houses on a block. Assuming each household is independent. What is the probability that all five households will have pets?
Answers
If the probability that a household owns a pet is 0.55 then the probability that all households will have pets is equal to 0.0503.
Given that the probability that a household owns a pet is 0.55 and there are 5 houses on a block.
We are required to calculate the probability that all the five households will have pets.
Probability is basicallly the chance of happening an event among all the events possible. It cannot be negative.
Binomial probability distribution is basically the probability calculations but in different combinations.
In this we have to calculate the probability that all the houses will have the pets then the probability that all five households will have pets is equal to \(5C_{5}(0.55)^{5} (1-0.55)^{0}\)
=1(0.0503)\((0.45)^{0}\)
=1*0.0503*1
=0.0503
Hence the probability that all the five households will have pets is equal to 0.0503.
Learn more about probability at https://brainly.com/question/24756209
#SPJ4
Water drains from a 60 gallon bath tub at a constant rate. It empties in 5
minutes. What is the rate?
Help me pls
Answers
Answer:
-12 gal / min
Step-by-step explanation:
-60/5=-12
HELP I NEED BOTH 50 PONITS
Verify that fand g are inverse functions. 4 points each
7. f(x) = 5x + 2; g(x) = (x−2)
8. f(x) = ½x − 7; g(x) = 2x + 14

Answers
The functions 7 are inverse functions while the functions 8 are not inverse functions
Verifying that fand g are inverse functions.To verify that f and g are inverse functions, we need to show that:
f(g(x)) = x for all values of x in the domain of gg(f(x)) = x for all values of x in the domain of fLet's apply these conditions to the given functions:
f(x) = 5x + 2; g(x) = (x−2)/5
f(g(x)) = f((x−2)/5) = 5((x−2)/5) + 2 = x − 2 + 2 = x
g(f(x)) = g(5x + 2) = ((5x + 2) − 2)/5 = 5x/5 = x
Since f(g(x)) = x and g(f(x)) = x, we can conclude that f and g are inverse functions.
f(x) = ½x − 7; g(x) = 2x + 14
f(g(x)) = f(2x + 14) = ½(2x + 14) − 7 = x
g(f(x)) = g(½x − 7) = 2(½x − 7) + 14 = x − 7 + 14 = x + 7
Since f(g(x)) = x and g(f(x)) ≠ x, we can conclude that f and g are not inverse functions.
Read more about inverse functions at
https://brainly.com/question/3831584
#SPJ1
There are 15 people in a room. Each person ate of a pizza. There was no pizza
remaining. How many pizzas were in the room?
Answers
Explanation:
If there are 15 people, and each person eats 1 pizza, there must be 15 pizzas.
trapezoid $abcd$ has bases $\overline{ab}$ and $\overline{cd}$. the extensions of the two legs of the trapezoid intersect at $p$. if $[abd]
Answers
The area of trapezoid $ABCD$ is $\frac{1}{2}h(a+b)$, where $h$ is the height of the trapezoid and $a$ and $b$ are the lengths of the bases $\overline{AB}$ and $\overline{CD}$, respectively.
To find the area of trapezoid $ABCD$, we need to know the lengths of the bases and the height. Let's assume that the lengths of the bases are $a$ and $b$, where $a > b$. The extensions of the legs of the trapezoid intersect at point $P$.
To calculate the area of the trapezoid, we need to find the height. Let's consider triangle $APB$ formed by the extension of the leg $\overline{AB}$, the extension of the leg $\overline{CD}$, and the line segment $\overline{AP}$. Since $\overline{AB}$ and $\overline{CD}$ are parallel, triangle $APB$ is similar to triangle $CPD$.
Using the similarity of triangles, we can set up the following proportion: $\frac{h}{a} = \frac{h+x}{b}$, where $x$ is the length of $\overline{PD}$. Cross-multiplying gives us $bh = ah + ax$. Rearranging the equation, we have $ax = (b-a)h$. Dividing both sides by $a$, we get $x = \frac{b-a}{a}h$.
Now, the height of the trapezoid, $h$, is the sum of the lengths of $\overline{AP}$ and $\overline{PD}$: $h = \overline{AP} + \overline{PD} = x + \frac{b-a}{a}h$. Simplifying the equation, we have $\frac{a}{a}h = x + \frac{b-a}{a}h$, which gives us $\frac{h}{a} = x + \frac{b-a}{a}h$.
Substituting the value of $x$, we have $\frac{h}{a} = \frac{b-a}{a}h + \frac{b-a}{a}h$. Simplifying further, we get $\frac{h}{a} = \frac{2(b-a)}{a}h$. Dividing both sides by $\frac{2(b-a)}{a}$, we find that $h = \frac{a}{2(b-a)}h$.
Finally, we can substitute the value of $h$ in the formula for the area of the trapezoid to find:
$[ABD] = \frac{1}{2}h(a+b) = \frac{1}{2}\left(\frac{a}{2(b-a)}h\right)(a+b) = \frac{a(a+b)}{4(b-a)}$.
The area of trapezoid $ABCD$ with bases $\overline{AB}$ and $\overline{CD}$ is given by $\frac{a(a+b)}{4(b-a)}$, where $a$ and $b$ are the lengths of the bases and $h$ is the height of the trapezoid.
To know more about Area, visit
https://brainly.com/question/25292087
#SPJ11
Which statement is true?

Answers
Answer: (d)
Step-by-step explanation:
For option (a)
\(\sqrt[m]{x}\sqrt[m]{y}=\sqrt[m]{xy}\)
for the same exponent, numbers multiply keeping exponent the same.
for option (b)
\(a\sqrt[n]{x} +b\sqrt[n]{y} =\left(a+b\right)\sqrt[n]{x}\)
for option (c)
\(\Rightarrow \dfrac{\sqrt[m]{x} }{\sqrt[m]{y} }=\sqrt[m]{\dfrac{x}{y}}\)
for option (d)
exponent multiplies
\(\therefore \left(\sqrt[m]{x^a} \right)^b=\sqrt[m]{x^{ab}}\)
option (d) is correct
If k ?s a positive integer, find the radius of convergence, R, of the series Sigma n = 0 to infinity (n!)^k+4/((k + 4)n)! x^n. R=
Answers
To find the radius of convergence, R, of the series
Σ (n!)^(k+4)/((k+4)n)! x^n
we can use the ratio test. The ratio test states that if
lim |a_(n+1)/a_n| = L as n approaches infinity,
then the series converges if L < 1 and diverges if L > 1.
Applying the ratio test to our series, we have:
|((n+1)!)^(k+4)/((k+4)(n+1))! x^(n+1)| / |(n!)^(k+4)/((k+4)n)! x^n|
Simplifying this expression, we get:
|n+1| |x| / (k+4)(n+1)
As n approaches infinity, the term |n+1| / (n+1) simplifies to 1, and the expression becomes:
|x| / (k+4)
For the series to converge, we need |x| / (k+4) < 1. This implies that the radius of convergence, R, is given by:
R = k + 4
Therefore, the radius of convergence, R, for the given series is k + 4.
Learn more about convergence here: brainly.com/question/32234460
#SPJ11
Bradley is a website designer. His client wants a blue, green, or purple themed
website, and he has selected 3 shades of green, 4 shades of purple, and 7 shades
of blue. What is the ratio of shades of purple to shades of green?
Answers
the answer would be 4 purple to 3 green
4:3
evaluate the scalar line integral ∫ c (3x y) ds, where c is the line segment from (−1,3) to (4,2).
Answers
The scalar line integral ∫ c (3x y) ds, where c is the line segment from (−1,3) to (4,2) is equal to 78√26/5
To evaluate the scalar line integral ∫ c (3x y) ds, where c is the line segment from (−1,3) to (4,2), we first need to parameterize the curve c.
Let t be the parameter such that
x = -1 + 5t,
y = 3 - t,
for 0 ≤ t ≤ 1.
The length of the curve c is given by the integral ∫ c ds, which can be calculated using the formula ∫ a to b \(√(dx/dt)^2 + (dy/dt)^2\) dt. Plugging in the values from the parameterization, we get
\(∫ c ds = ∫ 0 to 1 √(5^2 + (-1)^2) dt = ∫ 0 to 1 √26 dt = √26.\)
Using the parameterization, we can now write the integral as
\(∫ c (3x y) ds = ∫ 0 to 1 (3(-1+5t)(3-t)) √(5^2 + (-1)^2) dt = 78√26/5.\)
Therefore, the scalar line integral ∫ c (3x y) ds, where c is the line segment from (−1,3) to (4,2) is equal to 78√26/5.
Learn more about the scalar line integral
https://brainly.com/question/31392715
#SPJ4
The scalar line integral ∫ c (3x y) ds, where c is the line segment from (−1,3) to (4,2), is approximately equal to
22.229.
We can do this by letting x = t and y = 3 - t/2, where -1 ≤ t ≤ 4.
Then, we can find ds/dt using the formula \(ds/dt = \sqrt{(dx/dt^2 + dy/dt^2)}\), which simplifies to
\(ds/dt = \sqrt{(1 + 1/4) } = \sqrt{(5)/2} .\)
Next, we can substitute x and y in terms of t into the integrand and simplify to get:
\(3x y = 3t(3 - t/2) = 9t - (3/2)t^2\)
Now, we can evaluate the integral by integrating with respect to t from -1 to 4:
\(\int c (3x y) ds = ∫ from -1 to 4 (9t - (3/2)t^2) (\sqrt{(5)/2)} dt\)
\(= (\sqrt{(5)/2)} [ (9t^2/2) - (3/8)t^3 ] evaluated from -1 to 4\)
\(= (\sqrt{(5)/2)} [ (81/2) - (243/8) - (-27/8) + (3/8) ]\)
\(= \sqrt{(5)/2)} [ (189/8) ]\)
= 22.229
Therefore, the scalar line integral ∫ c (3x y) ds, where c is the line segment from (−1,3) to (4,2), is approximately equal to
22.229.
for such more question on scalar line integral
https://brainly.com/question/31392715
#SPJ11
among susceptible individuals exposed to a particular infectious agent 30% generally develop clinical disease. out of a random sample of 100 people suspected of exposure to the agent only 20 developed clinical disease. can this result be explained by chance alone? (use r to perform the test).
Answers
We draw the conclusion that the results are significantly different since the null hypothesis was rejected, which means that a different proportion of people than 0.3 had clinical illness.
Define null hypothesis.With the aid of a statistical test, researchers weigh the evidence in favor of and against the null and alternative hypotheses, which are two opposing claims: The null hypothesis (H0) states that there is no population impact. Alternative hypothesis (Ha or H1): The population is affected.
Given,
Among susceptible individuals exposed to a particular infectious agent 30% generally develop clinical disease. out of a random sample of 100 people suspected of exposure to the agent only 20 developed clinical disease.
Let X be the random variable to determine the proportion of people who have clinical illness.
n: The overall number of people who were exposed to a specific infectious pathogen.
p: The percentage of sample members who have a clinical illness.
Selected subjects who experience clinical disease are the experiment's success.
As a result, the variables are n = 100 and p = 0.30.
It is necessary to determine whether exposure to the agent outcome may be entirely accounted for by coincidence.
A P-value is a probabilistic indicator of the likelihood that an observed outcome effect is accidental.
Using the default level of significance = 0.05, the level of significance is not defined.
One percentage z-test is the best suitable test for the aforementioned assertion.
The alternate and null hypothesis is
H0: p = 0.3
H1:: p ≠ 0.3
Where p is the percentage of the population that develops a clinical illness.
R may be used to calculate the p-value and test statistic.
The instruction is as follows:
x = 20; n = 100; p = 0.3; prop.test
The result looks like this: - The p-value obtained from the output above is 0.03817.
Decision principle:
When significance is 5%,
If the p-value is below 0.05, reject the null hypothesis.
Accept the contrary.
Because the p-value was 0.03817 0.05
The null hypothesis is disproven.
In conclusion:
We draw the conclusion that the results are significantly different since the null hypothesis was rejected, which means that a different proportion of people than 0.3 had clinical illness.
To learn more about null hypothesis, visit:
https://brainly.com/question/28920252
#SPJ4
Determine whether the sequence converges or diverges. If it converges, find the limit. (If an answer does not exist, enter DNE.) an = (−1)^n/ 9√n
Answers
The given sequence converges to the limit -ln 3/2. The given sequence is an = \((-1)^{n/ 9\)√n.
We have to determine whether the sequence converges or diverges.
If it converges, find the limit. (If an answer does not exist, enter DNE.)
Let's calculate the first few terms of the given sequence:
n = 1; an = \((-1)^{1/9\)√1 = -1/9n = 2;
an = \((-1)^{2/9\)√2
= 1/9.3.
We notice that the terms of the sequence are oscillating in sign and decreasing in magnitude.
This suggests that the sequence might be converging.
Let's apply the alternating series test to confirm our conjecture.
Theorem (Alternating Series Test):
If an = \((-1)^{{n-1}bn\)
satisfies the following conditions:
1) bn > 0 for all n
2) bn is decreasing for all n
3) lim{n->∞} bn = 0
then the alternating series is convergent.
Moreover, the limit L lies between any two consecutive partial sums of the series.
Let's check the conditions for the given sequence.
1) bn = 1/9√n > 0 for all n
2) d/dn (1/9√n) = -1/(18n√n) < 0 for all n
3) lim{n->∞} 1/9√n = 0
We have checked all the conditions of the alternating series test, and hence the given sequence converges.
Let's find the limit using the formula for the sum of an infinite alternating series.
Limit = L = -ln 3/2.
So, the given sequence converges to the limit -ln 3/2.
To know more about converges visit:
https://brainly.in/question/29957083
#SPJ11
Internet Viewing A researcher wishes to estimate the average number of minutes per day a person spends on the Internet. How large a sample must she select if she wishes to be 90% confident that the population mean is within 13 minutes of the sample mean? Assume the population standard deviation is 46 minutes. Round your final answer up to the next whole number. The researcher needs a sample of at least people. Work Time Lost due to Accidents At a large company, the Director of Research found that the average work time lost by employees due to accidents was 98 hours per year. She used a random sample of 18 employees. The standard deviation of the sample was 5.2 hours. Estimate the population mean for the number of hours lost due to accidents for the company, using a 99% confidence interval. Assume the variable is normally distributed. Round intermediate answers to at least three decimal places. Round your final answers to the nearest whole number. Doctoral Student Salaries Full-time Ph.D. students receive an average of $12,837 per year. If the average salaries are normally distributed with a standard deviation of $1500, find the probabilities. Use a TI-83 Plus/TI-84 Plus calculator and round the answer to at least four decimal places. Part: 0/2 Part 1 of 2 (a) The student makes more than $17,000. P(X>17,000)-
Answers
Using the z-distribution, as we have the population standard deviation, it is found that a sample of 83 people must be taken.
Given,
Estimation of number of minutes per day a person spends on the internet .
Margin of error in Z distribution,
M = z σ/\(\sqrt{n}\)
In which:
z is the critical value.
σ is the population standard deviation.
n is the sample size.
Here,
We have 90% confidence level ,
Thus ,
\(\alpha\) = 0.9
z is the value of Z that has a p-value
(1+0.9) / 2
= 0.95
so the critical value is z = 2.575
Also we have
standard deviation = 46 minutes
Population mean = 13 minutes
To find minimum sample size solve for n
M = z σ/\(\sqrt{n}\)
13 = 2.575 (46/\(\sqrt{n}\))
n = 83 .30
Rounding up, a sample of 83 people must be taken.
More can be learned about the z-distribution at brainly.com/question/25890103
#SPJ4
A-123
B-57
C-90
D-33

Answers
Answer:
D
Step-by-step explanation: