Order these fractions and decimals from least to greatest.. ASAP please!!
7 1/10, 7.79, 7.108, 57/8
Answers
Answer:
7 1/10 , 7.108 , 57/8 , 7.79
Step-by-step explanation:
7/10 = 7.1
57/8 = 7.125
Related Questions
consider a 3x3 matrix a this matrix has -2 as an eigen value compute a basis of eigen space corresponding to eigen value -2
Answers
To compute a basis of the eigen space corresponding to eigen value -2, we need to find the null space of the matrix A + 2I, where A is the 3x3 matrix and I is the identity matrix.
The null space will give us the basis vectors of the eigen space
To find the eigen space corresponding to the eigen value -2, we start by constructing the matrix A + 2I, where A is the given 3x3 matrix and I is the 3x3 identity matrix. Next, we solve the homogeneous system of linear equations (A + 2I)x = 0, where x is a vector. The solutions to this system form the null space of the matrix A + 2I.
By finding a basis for this null space, we can obtain the basis vectors of the eigen space corresponding to the eigen value -2.
For more questions like Matrix click the link below:
https://brainly.com/question/29132693
#SPJ11
an unnormalized relation is a table that has more than one row.
Answers
An unnormalized relation refers to a table in a relational database that contains more than one row. This means that there are duplicate rows in the table, which violates the rules of normalization.
Normalization is a process in database design that aims to eliminate data redundancy and ensure data integrity. It involves breaking down a database into multiple tables and defining relationships between them. By doing so, we can efficiently store and retrieve data while minimizing inconsistencies.
In an unnormalized relation, duplicate rows can lead to various problems. For example, it can result in data inconsistencies, as updating one instance of a row may not reflect changes in other duplicate rows. Additionally, it can cause unnecessary storage and maintenance overhead.
To normalize an unnormalized relation, we need to identify the functional dependencies in the table and create separate tables for related data. This helps organize the data and reduces redundancy.
In summary, an unnormalized relation is a table in a relational database that has duplicate rows. It is important to normalize such relations to ensure data integrity and efficiency.
To know more about unnormalized relation click this link -
brainly.com/question/30888382
#SPJ11
Evaluate ∫3x2sin(x3)cos(x3)dx by
(a) using the substitution u=sin(x3) and
(b) using the substitution u=cos(x3).
Explain why the answers from (a) and (b) are seemingly very different
Answers
Answer:
Evaluate ∫3x2sin(x3)cos(x3)dx
Step-by-step explanation:
hello (a) using the substitution u=sin(x3) because
du =3x²(cos x3)dx
you have ∫3x2sin(x3)cos(x3)dx = ∫udu=u²/2 +c............continu
Is 15 1/2 to the right or left of 15 3/4 on the number line? Explain your answer.
Answers
Answer:
to the left
Step-by-step explanation:
Answer:
To the Left
15 1/4, 15 1/2, 15 3/4, 16
Hope this helps.
the product of a rational and irrational number is always
Answers
The product of a rational and an irrational number can be either rational or irrational, depending on the specific numbers involved.
To illustrate this, let's consider an example:
Let's say we have the rational number 2/3 and the irrational number √2.
Their product would be (2/3) * √2.
In this case, the product is irrational.
The square root of 2 is an irrational number, and when multiplied by a rational number, the result remains irrational.
However, it's also possible to have a product of a rational and an irrational number that is rational. For example, if we consider the rational number 1/2 and the irrational number √4, their product would be (1/2) * 2, which equals 1. In this case, the product is a rational number.
Therefore, we cannot make a definitive statement that the product of a rational and an irrational number is always rational or always irrational. It depends on the specific numbers involved in the multiplication.
To learn more about rational number
https://brainly.com/question/19079438
#SPJ11
.Choose ONE of the following questions below: 2. Tony and Haymitch are part of a scientific team studying thunderclouds. The team is about to launch a weather balloon into an active part of a cloud. Tony's rope is 7.8m long and makes an angle of 36° with the ground. Haymitch's rope is 5.9m long. Determine all the possible distances, between Tony and Haymitch. а 3. In the diagram below, the height of CD is 13 m. Determine the length of the bridge, from A to B, and the measure of the angle
Answers
I'll address question 2:We have two sides and the included angle, so we can use the following formula d² = 7.8² + 5.9² - 2(7.8)(5.9)cos(36°)
To determine all the possible distances between Tony and Haymitch, we can use the Law of Cosines. Let's denote the distance between Tony and Haymitch as "d". We have two sides and the included angle, so we can use the following formula:
d² = 7.8² + 5.9² - 2(7.8)(5.9)cos(36°)
By substituting the values into the equation, we can calculate the distance "d". After obtaining the numerical value, we will have the possible distances between Tony and Haymitch.
In this question, we have two individuals, Tony and Haymitch, who are part of a scientific team studying thunderclouds. They are located at different points and we need to determine all the possible distances between them.
To solve this problem, we can use the Law of Cosines, which relates the lengths of the sides of a triangle to the cosine of one of its angles. In this case, we have a triangle formed by Tony, Haymitch, and the location where the weather balloon will be launched.
We are given that Tony's rope is 7.8m long and makes an angle of 36° with the ground. Haymitch's rope is 5.9m long. To find the possible distances between Tony and Haymitch, we need to calculate the length of the third side of the triangle, which represents the distance between them.
Using the Law of Cosines, we can substitute the given lengths and angle into the formula and solve for the unknown distance "d". By calculating the expression, we obtain the squared value of "d". Taking the square root of this value will give us the possible distances between Tony and Haymitch.
In conclusion, by applying the Law of Cosines and calculating the distance using the given lengths and angle, we can determine all the possible distances between Tony and Haymitch.
To know more about angle click here
brainly.com/question/14569348
#SPJ11
please help me. find the value of m and n.
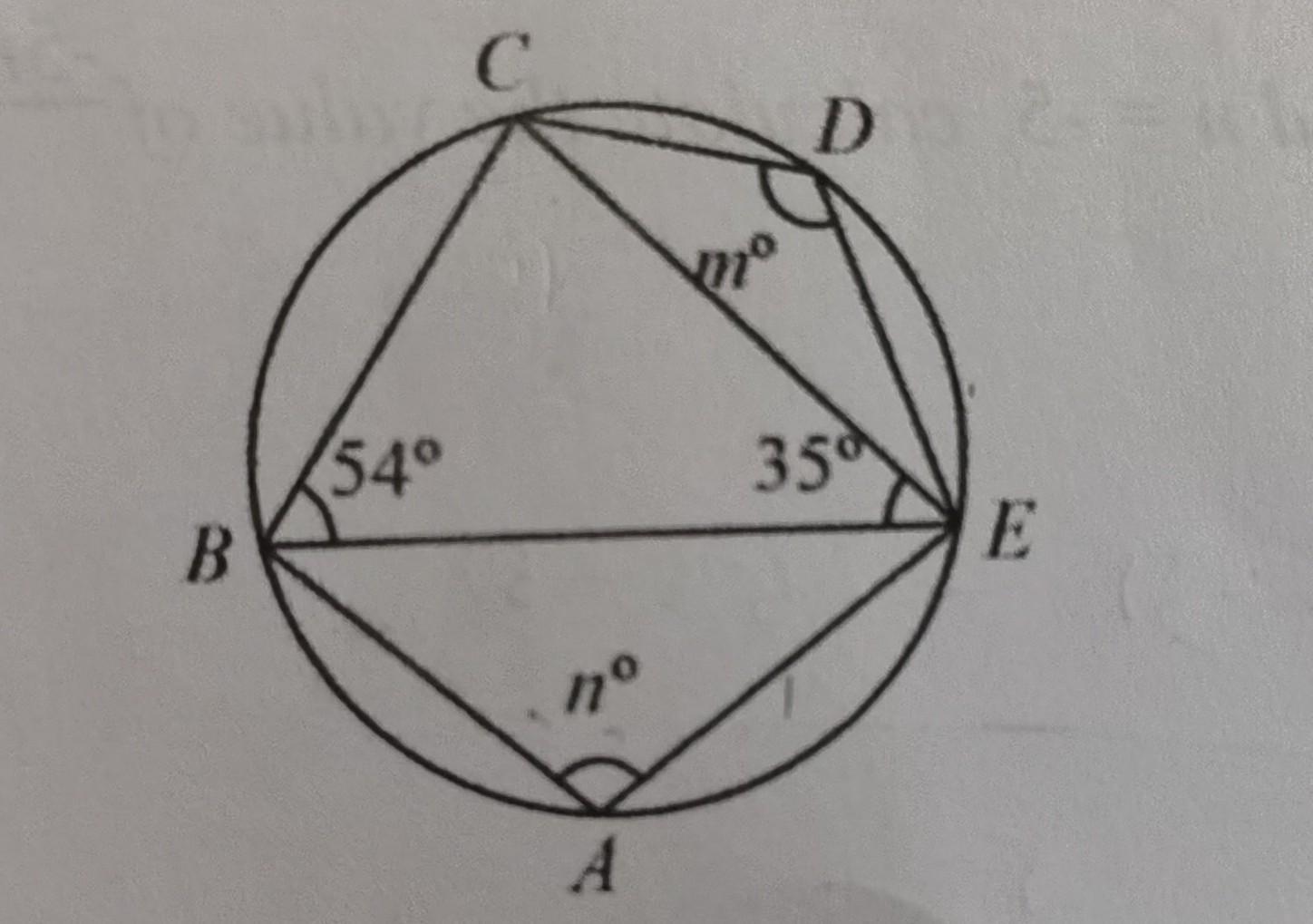
Answers
Answer:
in a hexqagan it adds up
Step-by-step explanation:
in a hexagan it adds up to 540
in a truangle 180
35+54=89
180-89=91
35+54+89+m+n=560
im not sure the anwser but heres some working out that might help
4+7x=3x+4+4x I need help
Answers
Answer:
0
Step-by-step explanation:
move x's to one side and constants to another
7x-3x-4x=4-4
add constants and combine like terms
0=0
The rectangle shown has a perimeter of 98 cm and the given area. Its length is 7 more than 5 times its width. Write and solve a system of equations to find the dimensions of the rectangle.
Answers
Answer:
35 is its width and 63 is its length.
Step-by-step explanation:
7 x 5 = 35 and 98 - 35 equals 63 which is the length.
Give an example of when you would encounter different types of fractions in the
real world.
Answers
Step-by-step explanation:
when I had to share a bar of chocolate with 3 of my cousins....... the bar had a size of 18 cm and there were 3 of us so we divided it by 3 (18÷3) and ended up with 6, so 6cm/cousin..... ..
b) if your friend wants to be as happy as possible, how many cheeseburgers should he eat? How do you know ? Answer question B

Answers
Answer:
Find out what x should be the apply by the power of 2 then you should be good
$1 at 3% for 50 years
Find the simple interest
Answers
Answer:
$1.50
Step-by-step explanation:
Simple interest is based on the principal amount of a loan or deposit, whereas compound interest is based on the principal amount and the interest that accumulates on it in every period.
Simple Interest = P x r x n
where P = Principal amount, r = Annual interest rate, n = Term of loan, in years
3% = 3 ÷ 100 = 0.03 so r = 0.03
Therefore, Simple Interest = 1 x 0.03 x 50 = 1.5
So the simple interest will be $1.50
I need help quick!
Q: The measure of

Answers
Answer:
x=34
Step-by-step explanation:
132-64=
68/2=
34
PLEASE MAKE ME BRAINLIEST
\( \frac{1 }{4 } \times \frac{3}{4} \div \frac{10}{3} \)
What is the answer to the above equation?
Answers
Answer:
Step-by-step explanation:
Solution
This (after combining the top 2 fractions, is a 4 tier fraction.
1/4*3/4 = 3/16
So the question now becomes 3/16 ÷ 10/3
The rule for such a question is invert (turn up side down) the second fraction and multiply.
3/16 * 3/10 Combine
(3*3)/(16* 10)
9 / 160
0.05625
\(\bf{\dfrac{1}{4}\times\dfrac{3}{4}\div\dfrac{10}{3} }\)
Multiply 1/4 by 3/4 (to do this, multiply the numerator by the numerator and the denominator by the denominator).
\(\bf{\dfrac{1\times3}{4\times4}\div\dfrac{10}{3} \ \ \to \ \ \ Multiply.}\)
Do the multiplications in the fraction 1 × 3 / 4 × 4.
\(\bf{\dfrac{3}{16}\div\dfrac{10}{3} }\)
Divide 3/16 by 10/3 by multiplying 3/16 by the reciprocal of 10/3.
\(\bf{\dfrac{3}{16}\times\left(\dfrac{3}{10}\right) }\)
Multiply 3/16 by 3/10 (to do this, multiply the numerator by the numerator and the denominator by the denominator).
\(\bf{\dfrac{3\times3}{16\times10 } \ \ \to \ \ \ Multiply }\)
Do the multiplications in the fraction 3 × 3 / 16 × 10
\(\bf{\dfrac{9}{160} \ \ \to \ \ Answer }\)
\(\huge \red{\boxed{\green{\boxed{\boldsymbol{\purple{Pisces04}}}}}}\)
8+x=x
what is x? i need help please. will mark brainliest!
Answers
Answer:
It has no solutions
Step-by-step explanation:
Rearrange the terms
\(8+x=x\\x + 8 =x\)
Subtract 8 from both sides
\(x + 8 - 8=x-8\)
Simplify
\(x = x-8\)
Subtract x from both sides
\(x - x = x - 8 - x\)
Simplify
\(0 = -8\)
The input is a contradiction: it has no solutions
to can be driven before it would need to be junked is an exponential random variable with parameter smith has a used car that he claims has been driven only 10,000 miles. if jones purchases the car, what is the
Answers
Answer:
2334
Step-by-step explanation:
The three sides of a triangle are in different colors – blue, green and red. The ratio of the length of the blue side to the length of the green side to the length of the red side is 3 : 4 : 5. The perimeter of the triangle is 240 cm. a) Fill in the blank: ___ units = 240 cm b) Fill in the blank: 1 unit = ___ cm c) What is the length of the red side of the triangle?
Answers
Answer:
The perimeter is the distance around the triangle. Given the ratio, the perimeter using the ratio is;
= 3 + 4 + 5
= 12 units
a. 12 units = 240 cm
The perimeter in centimetres is 240cm and in ratio is 12 units so they are equivalent.
b. 1 unit = 20 cm
If 12 units are to 240 cm, 1 unit is;
= 240/12
= 20 cm
c. Length of red side;
Red side has length of 5 units. 1 unit is 20 cm.
Length in cm is;
= 5 * 20
= 100 cm
what is 238 rouned to the nearst houndred
Answers
250 or higher is 300
249 or lower is 200
Answer:
200
Step-by-step explanation:
The owner of a new restaurant is designing the floor plan, and he is deciding between two different seating arrangements. The first plan consists of 10 tables and 25 booths, which will seat a total of 225 people. The second plan consists of 10 tables and 21 booths, which will seat a total of 197 people. How many people can be seated at each type of table?
Answers
An equation is formed of two equal expressions. The number of people that can sit at a table is 6.
What is an equation?An equation is formed when two equal expressions are equated together with the help of an equal sign '='.
Let the number of people that can be seated at a table be represented by x, while the number of people that can be seated in a booth is y.
The equation for the two floor plans can be written as,
24x + 11y = 254
12x + 17y = 242
Solving the above equations, by plotting the two of the given equations. Therefore, the number of people that can sit at a table is 6.
Learn more about Equation:
https://brainly.com/question/2263981
#SPJ1

Graph then find the following: a) Domain b) Range c) Vertex d) Axis of symmetry e) Minimum f) Maximum g) Stretch or shrink h) Upward/downward: A) f(x)=x² B) f(x) = -3x²

Answers
Step-by-step explanation:
a) Domain of both functions is all real numbers (-∞, +∞), as there are no restrictions on the input (x).
b) The range of A) f(x)=x² /3 is [0, +∞), as the minimum value of the function is 0 and there is no maximum value.
The range of B) f(x) = -3x² is (-∞, 0], as the maximum value of the function is 0 and there is no minimum value.
c) The vertex of A) f(x)=x² /3 is at (0,0).
The vertex of B) f(x) = -3x² is at (0,0).
d) The axis of symmetry of both functions is the vertical line passing through the vertex, which is x = 0.
e) The minimum value of A) f(x)=x² /3 is 0, which occurs at the vertex.
f) The maximum value of B) f(x) = -3x² is 0, which occurs at the vertex.
g) A) f(x)=x² /3 is a horizontally shrunk version of the parent function f(x) = x² by a factor of 1/3.
B) f(x) = -3x² is a vertically stretched version of the parent function f(x) = x² by a factor of 3.
h) A) f(x)=x² /3 opens upward, as the coefficient of x² is positive.
B) f(x) = -3x² opens downward, as the coefficient of x² is negative.
what is the slope of the line? help plz

Answers
Answer:
the answer is negative 2
Point M is the midpoint of line segment CD,
shown below.
What are the coordinates of point M?
C (6,10)
M
D (20, 18)
Answers
Answer:
M(13, 14)-------------------------
Each coordinate of the midpoint is the average of endpoints:
x = (6 + 20)/2 = 26/2 = 13y = (10 + 18)/2 = 28/2 = 14Therefore M is (13, 14).
in how many ways can n identical balls be distributed into r bins such that each bin contains at least two balls
Answers
Ways can n identical balls be distributed into r bins such that each bin contains at least two balls are 20 ways.
1 ball in each of 3 boxes: 4 ways
3 balls in one box: 4 ways
2 balls in one box and 1 ball in another box: 3*4=12 ways
There are 20 ways to arrange the balls .
In mathematics, a combination is a way of selecting items from a collection where the order of selection does not matter. Suppose we have a set of three numbers P, Q and R. Then in how many ways we can select two numbers from each set, is defined by combination.
The combination can also be represented as: –nCr, nCr, C(n,r), Crn
Proof:
nPr = nCr.r!
= [n!/r!(n-r)!].r!
= n!/(n-r)!
Hence the theorem states true.
A permutation is an act of arranging objects or numbers in order. Combinations are the way of selecting objects or numbers from a group of objects or collections, in such a way that the order of the objects does not matter.
Learn more about distribution here:-
brainly.com/question/29062095
#SPJ4
(1 point) (Exercise 1.1) Consider the amount function A(t)=t
2
+2t+4 a) Find the corresponding accumulation function a(t)= help (formulas) b) Find I
n
= help (formulas) Note: You can eam partial credit on this problem.
Answers
(a)The corresponding accumulation function a(t) is obtained by integrating A(t) with respect to t. Integration is the reverse process of differentiation, i.e., it undoes the effect of differentiation.
= ∫(t²+2t+4)dt
= [t³/3+t²+4t]+C , where C is the constant of integration.
Thus, the accumulation function a(t) is given by a(t) = ∫(t²+2t+4)dt = t³/3+t²+4t+C
(b)To find ㏑, we integrate the difference between a and b with respect to t and evaluate it between the limits n and 0.
=∫₀ⁿ
=〖(a(t)-b(t)) dt= a(n)-a(0)-[b(n)-b(0)] 〗
= [n³/3+n²+4n]-[0+0+0]-[n²/2-2n-4]
= n³/3+3n²/2+6n-4
Thus, ㏑= n³/3+3n²/2+6n-4.
learn more about the accumulation function: https://brainly.com/question/12231722
#SPJ11
Simplify: 3−5(−3n+5)3−5(−3n+5)
Answers
Answer:
\(60n - 97\)
Step-by-step explanation:
\(3 - 5( - 3n + 5)3 - 5( - 3n + 5)\)
\(3 + (15n - 25)3 + 15n - 25\)
\(3 + 45n - 75 + 15n - 25\)
\(60n - 97\)
Simplify each expression by combining like terms
a). x + 2x
b). 3m + 4n - 6n
Answers
Answer:
1) 3x
2) 3m - 2n
Answer:
below
Step-by-step explanation:
3x, 3 m − 2 n
Prove that the angle that an arc of a circle ubtend at the Centre i twice that which it ubtend at any point on the remaining part of the circumference
Answers
Therefore , the solution of the given problem of circumference statement is proved by the following below explanation.
What is circumference?Any great circle's circumference, or the distance between the center of the sphere and any plane running through it, is measured in meters. Any large circle that passes through a pole-designated location is referred to as a meridian.
Here,
An arc PQ of a circle that subtends angles POQ at its center O and PAQ at one of its points A on the circumference.
To prove : <POQ = 2<PAQ
To prove this theorem we consider the arc AB in three different situations, minor arc AB, major arc AB and semi-circle AB.
Construction:
Join the line AO extended to B.
Proof :
<BOQ = ZOAQ + ZAQO .....(1)
Also, in A OAQ,
OA = OQ
Therefore,
[Radii of a circle]
ZOAQ = ZOQA
[Angles opposite to equal sides are equal]
<BOQ = 2ZOAQ
.......(2)
Similarly, BOP = 220AP
.(3)
Adding 2 & 3, we get,
<BOP + <BOQ = 2(ZOAP + ZOAQ)
<POQ = 2<PAQ
.......(4)
For the case 3, where PQ is the major arc, equation 4 is replaced by
Reflex angle, <POQ = 2ZPAQ
Therefore , the solution of the given problem of circumference statement is proved by the following below explanation.
To know more about circumference , visit
https://brainly.com/question/28757341
#SPJ4
A STEAM tutoring center offers a robotics class and an app development class to its members. There are 280 members, all of which are registered for at least one class this spring. If 75% of members registered for a robotics class and 50% registered for an app development class, how many members registered for both robotics and app development?
Answers
The number of students who registered for both robotics and app development is 70.
What is a percentage?The percentage is calculated by dividing the required value by the total value and multiplying by 100.
Example:
Required percentage value = a
total value = b
Percentage = a/b x 100
Example:
50% = 50/100 = 1/2
25% = 25/100 = 1/4
20% = 20/100 = 1/5
10% = 10/100 = 1/10
We have,
Total members = 280
The number of members who registered for the robotics class.
= 75% of 280
= 3/4 x 280
= 3 x 70
= 210
The number of members who registered for the app development class
= 50% of 280
= 1/2 x 280
= 140
We see that,
210 + 140 = 350
But we have 280 members.
So,
The number of students who registered for both robotics and app development.
= 350 - 280
= 70
Thus,
The number of students who registered for both robotics and app development is 70.
Learn more about percentages here:
https://brainly.com/question/11403063
#SPJ1
Can anyone please help me I need help I need help please help me

Answers
Answer: 1/64
Step-by-step explanation:
Your answer is correct. (x²)³=x⁶. Everytime you see parenthesis separating exponents, it means to multiply. 2×3=6.
Since we know that x=1/2, we can plug in 1/2.
(1/2)⁶=1/64
( you will get brainlist and 100 points and a 5.0 and thanks if you do this!!)
Step 2. Identify three (3) regions of the world. Think about what these regions have in common.
Step 3. Conduct internet research to identify commonalities (things that are alike) about the three (3) regions that you chose for this assignment. You should include at least five (5) commonalities. Write a report about your findings.
Answers
Report on Commonalities Among Three Chosen Regions
For this assignment, three regions of the world have been selected to identify commonalities among them. The chosen regions are North America, Europe, and East Asia. Through internet research, several commonalities have been identified that are shared among these regions. Below are five commonalities found:
Economic Development:
All three regions, North America, Europe, and East Asia, are characterized by significant economic development. They are home to some of the world's largest economies, such as the United States, Germany, China, and Japan. These regions exhibit high levels of industrialization, technological advancement, and trade activities. Their economies contribute significantly to global GDP and are major players in international commerce.
Technological Advancement:
Another commonality among these regions is their emphasis on technological advancement. They are known for their innovation, research and development, and technological infrastructure. Companies and industries in these regions are at the forefront of technological advancements in fields such as information technology, automotive manufacturing, aerospace, pharmaceuticals, and more.
Cultural Diversity:
North America, Europe, and East Asia are culturally diverse regions, with a rich tapestry of different ethnicities, languages, and traditions. Immigration and historical influences have contributed to the diversity seen in these regions. Each region has a unique blend of cultural practices, cuisines, art, music, and literature. This diversity creates vibrant multicultural societies and fosters an environment of cultural exchange and appreciation.
Democratic Governance:
A commonality shared among these regions is the prevalence of democratic governance systems. Many countries within these regions have democratic political systems, where citizens have the right to participate in the political process, elect representatives, and enjoy individual freedoms and rights. The principles of democracy, rule of law, and respect for human rights are important pillars in these regions.
Education and Research Excellence:
North America, Europe, and East Asia are known for their strong education systems and institutions of higher learning. These regions are home to prestigious universities, research centers, and educational initiatives that promote academic excellence. They attract students and scholars from around the world, offering a wide range of educational opportunities and contributing to advancements in various fields of study.
In conclusion, the regions of North America, Europe, and East Asia share several commonalities. These include economic development, technological advancement, cultural diversity, democratic governance, and education and research excellence. Despite their geographical and historical differences, these regions exhibit similar traits that contribute to their global significance and influence.
Answer:
For this assignment, three regions of the world have been selected to identify commonalities among them. The chosen regions are North America, Europe, and East Asia. Through internet research, several commonalities have been identified that are shared among these regions. Below are five commonalities found:
Economic Development:
All three regions, North America, Europe, and East Asia, are characterized by significant economic development. They are home to some of the world's largest economies, such as the United States, Germany, China, and Japan. These regions exhibit high levels of industrialization, technological advancement, and trade activities. Their economies contribute significantly to global GDP and are major players in international commerce.
Technological Advancement:
Another commonality among these regions is their emphasis on technological advancement. They are known for their innovation, research and development, and technological infrastructure. Companies and industries in these regions are at the forefront of technological advancements in fields such as information technology, automotive manufacturing, aerospace, pharmaceuticals, and more.
Cultural Diversity:
North America, Europe, and East Asia are culturally diverse regions, with a rich tapestry of different ethnicities, languages, and traditions. Immigration and historical influences have contributed to the diversity seen in these regions. Each region has a unique blend of cultural practices, cuisines, art, music, and literature. This diversity creates vibrant multicultural societies and fosters an environment of cultural exchange and appreciation.
Democratic Governance:
A commonality shared among these regions is the prevalence of democratic governance systems. Many countries within these regions have democratic political systems, where citizens have the right to participate in the political process, elect representatives, and enjoy individual freedoms and rights. The principles of democracy, rule of law, and respect for human rights are important pillars in these regions.
Education and Research Excellence:
North America, Europe, and East Asia are known for their strong education systems and institutions of higher learning. These regions are home to prestigious universities, research centers, and educational initiatives that promote academic excellence. They attract students and scholars from around the world, offering a wide range of educational opportunities and contributing to advancements in various fields of study.
In conclusion, the regions of North America, Europe, and East Asia share several commonalities. These include economic development, technological advancement, cultural diversity, democratic governance, and education and research excellence. Despite their geographical and historical differences, these regions exhibit similar traits that contribute to their global significance and influence.