Order the integers from least to greatest.
-5, 8, -3, 10, -9,0
Answers
Answer:
-9, -5, -3, 0, 8, 10
I hope this helps!
Answer:
-9, -5, -3, 0 8, 10
Step-by-step explanation:
Negative is less than positive
Related Questions
The sum of the two roots of a quadratic is 21. The product of those two roots is 104. Given that both roots are positive, what is the difference of the two roots of the quadratic?
Answers
Answer:
The difference of the two roots of the quadratic is 5
Step-by-step explanation:
Let the two roots be a and b
Sum of the roots is 21
a + b = 21 ••••••••(i)
Product of the roots is 104
ab = 104 •••••••(ii)
we want to find a - b
a = 104/b
Put this into 1
104/b + b = 21
Multiply through by b
104 + b^2 = 21b
Thus;
b^2 - 21b + 104 = 0
b^2 -13b - 8b + 104 = 0
b(b-13) -8(b -13) = 0
(b-8)(b-13) = 0
b = 8 or 13
From above;
b = 104/a
So a is 104/13 or 104/8 = 13 or 8
So the difference between the roots will just be 13-8 = 5
The table below shows some inputs and outputs of function f(x). _1 0 2 4 8 f(a) 1 5 13 21 37 Which statement best describes the function? O f(x) is a linear function because z and f(z) are both increasing. O f(2) is an absolute value function because 2 and f(a) are both increasing. O f(z) is a linear function because f(z) is increasing by 4 for each increase in z by 1.
Answers
A statement which best describes the function include the following: A. f(x) is a linear function because x and f(x) are both increasing.
What is a linear function?In Mathematics, a linear function can be defined as a type of function whose equation is graphically represented by a straight line on the cartesian coordinate. This ultimately implies that, a linear function has the same slope and it is typically used for uniquely mapping an input variable to an output variable, which both increases simultaneously.
Next, we would determine the slope by using the points contained in the table as follows;
Slope (m) = (Change in y-axis, Δy)/(Change in x-axis, Δx)
Slope (m) = (y₂ - y₁)/(x₂ - x₁)
Slope (m) = (5 - 1)/(0 + 1)
Slope (m) = 4.
Slope (m) = (13 - 5)/(2 - 0)
Slope (m) = 4
Slope (m) = (21 - 13)/(4-2)
Slope (m) = 8/2 = 4.
Read more on slope here: brainly.com/question/23086745
#SPJ1
2Geometry help please!! will mark brainliest

Answers
Answer:
BC = 7
Step-by-step explanation:
x + 2 = 5
x = 3
this would also work for sides BC and AD.
(3 x 3) - 2 = 9 - 2 = 7
3 + 4 = 7
test the hypothesis that the mean weight of the two sheets is equal (μ1−μ2)against the alternative that it is not (and assume equal variances). find the t-stat to 3 decimal places.
Answers
To test the hypothesis that the mean weight of two sheets is equal (μ1 - μ2) against the alternative that it is not, and assuming equal variances, we can use a two-sample t-test. The t-statistic can be calculated using the following formula:
t = (x1 - x2) / (s_p * sqrt(1/n1 + 1/n2))
where:
x1 and x2 are the sample means of the two sheets,
s_p is the pooled standard deviation,
n1 and n2 are the sample sizes.
The pooled standard deviation (s_p) can be calculated using the following formula:
s_p = sqrt(((n1 - 1) * s1^2 + (n2 - 1) * s2^2) / (n1 + n2 - 2))
where:
s1 and s2 are the sample standard deviations.
To calculate the t-statistic, we need the sample means, sample standard deviations, and sample sizes.
Once you provide the specific values for these variables, I can assist you in calculating the t-statistic to 3 decimal places.
To learn more about equal variances: -brainly.com/question/30777199
#SPJ11
To test the hypothesis that the mean weight of the two sheets is equal (μ1 - μ2) against the alternative that it is not, we can use a paired t-test assuming equal variances. The paired t-test is used when we have paired data or measurements on the same subjects or objects.
The t-statistic for a paired t-test is calculated as follows:
t = (X1 - X2) / (s / √n)
where X1 and X2 are the sample means of the two samples, s is the pooled standard deviation, and n is the number of pairs.
Please provide the sample means, standard deviation, and sample size for each sheet so that we can calculate the t-statistic to 3 decimal places.
To learn more about equal variances: -brainly.com/question/30777199
#SPJ11
Is this correct?????????

Answers
Answer:
yup its right
Step-by-step explanation:
20 POINTS
A student starts a walk at (−6, 10). If the student walks 4 miles north, south, east, or west, which of the following could be their location at the end of the walk?
A (10, −6), (6, −6), (−2, 14), (−10, 14)
B (4, 10), (−14, 10), (−6, −2), (−6, 6)
C (−6, 4), (−6, 6), (−2, 10), (4, 10)
D (−10, 10), (−2, 10), (−6, 14), (−6, 6)
Answers
Check the picture below.

Answer:
D
Step-by-step explanation:
First we can start with north and south. This menas the y value is affected and not the x.
(-6, 10) The y(10) can have +4 and -4, which is 14 and 6. D has both (-6, 14) and (-6, 6)
For East and west, x is changed and right is not so
(-6, 10) The x(-6) can have +4 and -4, which is -2 and -10, D has both (-10, 10) (-2, 10)
That's why D is the right answer
Given data on shoulder girth and height of a group of individuals. The mean shoulder girth is 107. 20 cm with a standard deviation of 10. 37 cm. The mean height is 171. 14 cm with a standard deviation of 9. 41 cm. The correlation between height and shoulder girth is 0. 67.
Write the equation of the regression line for predicting height
Answers
The equation of the regression line for predicting height based on shoulder girth is:y = 103.82 + 0.607x, which mean that for every one-unit increase in shoulder girth, the predicted height increase by 0.607 units.
Since the equation of the regression line for predicting height based on shoulder girth can be written as: y = a + bx, where y is the predicted height, x is the shoulder girth, a is the y-intercept, and b is the slope of the regression line.
To find the values of a and b, we need to use the following formulas:
b = r(Sy/Sx)
a = ybar - b(xbar), where r is the correlation coefficient between height and shoulder girth, Sy is the standard deviation of height, Sx is the standard deviation of shoulder girth, ybar is the mean height, and x bar is the mean shoulder girth. now substituting the values we get :
b = 0.67(9.41/10.37) ≈ 0.607
a = 171.14 - 0.607(107.20) ≈ 103.82
To know more about the correlation coefficient refer to the link brainly.com/question/27226153
#SPJ4
find the derivative of the function.
f(x) = log8(x)
h(x) = log5(x + 9)
h(x) = e^x8 − x + 3
g(x) = 2^x
Answers
The derivatives of the following functions are
1. Derivative of the f(x) = log8(x) is f'(x) = (1 / x) * (1 / ln(8)).
2. Derivative of the h(x) = log5(x + 9) is h'(x) = (1 / (x + 9)) * (1 / ln(5)).
3. Derivative of the h(x) = e^x^8 − x + 3 is h'(x) = e^(x^8 - x + 3) * (8x^7 - 1).
4. Derivative of the g(x) = 2^x is g'(x) = 2^x * ln(2).
1. For the function f(x) = log8(x), find its derivative:
To find the derivative of f(x) with respect to x, we can use the change of base formula for logarithms and the chain rule:
f(x) = log8(x) = ln(x) / ln(8)
f'(x) = (1 / x) * (1 / ln(8))
2. For the function h(x) = log5(x + 9), find its derivative:
Similar to the previous function, use the change of base formula and the chain rule:
h(x) = log5(x + 9) = ln(x + 9) / ln(5)
h'(x) = (1 / (x + 9)) * (1 / ln(5))
3. For the function h(x) = e^(x^8 − x + 3), find its derivative:
Apply the chain rule:
h'(x) = e^(x^8 - x + 3) * (8x^7 - 1)
4. For the function g(x) = 2^x, find its derivative:
Use the exponential rule and the chain rule:
g'(x) = 2^x * ln(2)
To learn more about derivatives of the function:
https://brainly.com/question/16957010
#SPJ11
In the given figure ABCD, prove that
angleBCD= angleBAD+ angle ABC+angle ADC.
[Hint: Join A and C then extended AC to the point E]

Answers
We have proved that Angle BCD is equal to angle BAD plus angle ABC plus angle ADC, as required.
To prove that angle BCD is equal to angle BAD plus angle ABC plus angle ADC, we can use the following steps:
Step 1: Join points A and C with a line segment. Let's label the point where AC intersects with line segment BD as point E.
Step 2: Since line segment AC is drawn, we can consider triangle ABC and triangle ADC separately.
Step 3: In triangle ABC, we have angle B + angle ABC + angle BCA = 180 degrees (due to the sum of angles in a triangle).
Step 4: In triangle ADC, we have angle D + angle ADC + angle CDA = 180 degrees.
Step 5: From steps 3 and 4, we can deduce that angle B + angle ABC + angle BCA + angle D + angle ADC + angle CDA = 360 degrees (by adding the equations from steps 3 and 4).
Step 6: Consider quadrilateral ABED. The sum of angles in a quadrilateral is 360 degrees.
Step 7: In quadrilateral ABED, we have angle BAD + angle ABC + angle BCD + angle CDA = 360 degrees.
Step 8: Comparing steps 5 and 7, we can conclude that angle B + angle BCD + angle D = angle BAD + angle ABC + angle ADC.
Step 9: Rearranging step 8, we get angle BCD = angle BAD + angle ABC + angle ADC.
Therefore, we have proved that angle BCD is equal to angle BAD plus angle ABC plus angle ADC, as required.
For more questions on Angle .
https://brainly.com/question/31615777
#SPJ8
Given: Quadrilateral \(\displaystyle\sf ABCD\)
To prove: \(\displaystyle\sf \angle BCD = \angle BAD + \angle ABC + \angle ADC\)
Proof:
1. Draw segment \(\displaystyle\sf AC\) and extend it to point \(\displaystyle\sf E\).
2. Consider triangle \(\displaystyle\sf ACD\) and triangle \(\displaystyle\sf BCE\).
3. In triangle \(\displaystyle\sf ACD\):
- \(\displaystyle\sf \angle ACD = \angle BAD + \angle ADC\) (Angles of a triangle add up to \(\displaystyle\sf 180^\circ\)).4. In triangle \(\displaystyle\sf BCE\):
- \(\displaystyle\sf \angle BCE = \angle BAD + \angle ABC\) (Angles of a triangle add up to \(\displaystyle\sf 180^\circ\)).5. Since \(\displaystyle\sf \angle BCE\) and \(\displaystyle\sf \angle BCD\) are corresponding angles formed by transversal \(\displaystyle\sf BE\):
- \(\displaystyle\sf \angle BCE = \angle BCD\).6. Combining the equations from steps 3 and 4:
- \(\displaystyle\sf \angle BCD = \angle ACD = \angle BAD + \angle ADC\). - \(\displaystyle\sf \angle BCD = \angle BCE = \angle BAD + \angle ABC + \angle ADC\).Therefore, we have proven that in quadrilateral \(\displaystyle\sf ABCD\), \(\displaystyle\sf \angle BCD = \angle BAD + \angle ABC + \angle ADC\).
\(\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}\)
♥️ \(\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}\)
Which of the following functions represents the graph on
the left? (Hint: Plug in your x values from the previous
slide. Do they produce f(x)=0?)
O f(x) = (x-6)(x+2)
O f(x) = (x+6) (x - 2)
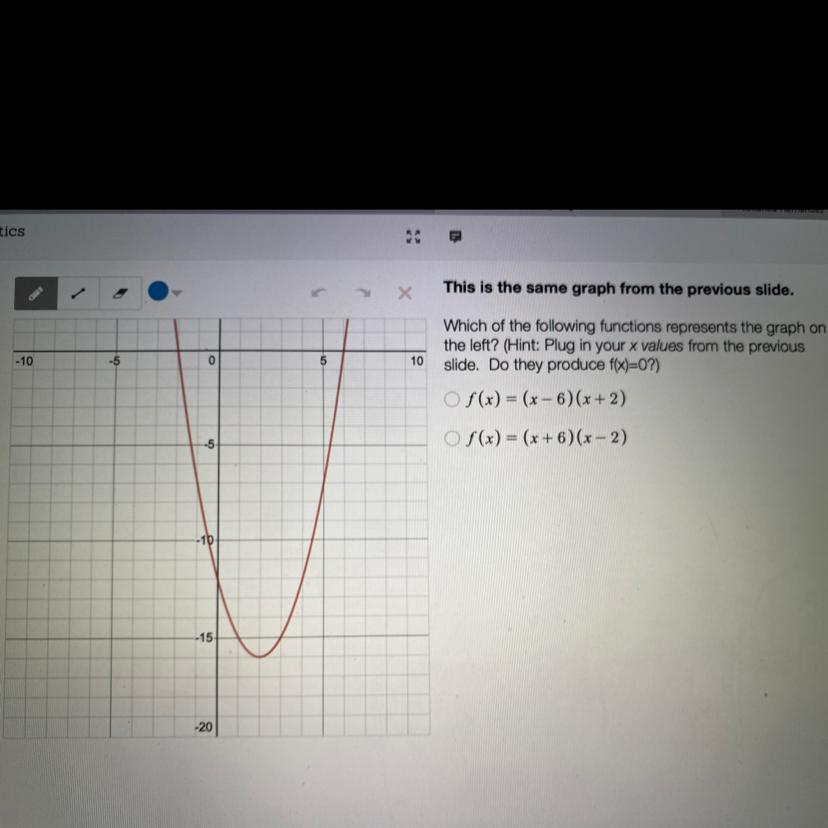
Answers
9514 1404 393
Answer:
f(x) = (x -6)(x +2)
Step-by-step explanation:
The graph shows the x-intercepts are -2 and +6. The factors will be binomials such that these values make the factors zero: (x +2) and (x -6).
f(x) = (x -6)(x +2)
grade 9 math
useing frist diff is this a linear relation yes or no show your work

Answers
Answer:
not linear since all first differences are not equal
Step-by-step explanation:
To find the first differences, subtract each y value from the next y value.
Use only y values.
here are the 4 first differences you need to calculate.
1 - 0 = 1
4 - 1 = 3
9 - 4 = 5
16 - 9 = 7
Now you place them in the appropriate column in the table.
x y first difference
0 0 1
1 1 3
2 4 5
3 9 7
4 16
If the first differences were all equal, the function would be a linear function.
In this case, the first differences are all different, 1, 3, 5, 7, so the function is not linear.
can someone help me on this? Will give brainlist.

Answers
Answer:
960????
Step-by-step explanation:
this may be wrong, but its an answer ;;v;;
the formula is:
b * h * length * 0.5
Para determinar las ganancias en colones, por concepto de entradas a un museo se usa la fórmula 3000x + 1500y + 1500z, en la x corresponde a la cantidad de adultos que ingresan;y, a la de los niños, y z, a la de los adultos mayores. ¿Cuál fue la ganancia del museo durante un fin de semana si ingresaron 38 adultos, 56 niños y 15 adultos mayores?
PORFA AYUDENMEN!
Answers
what is the solution to the system of equations? 5x+3y=18 and 2x-3y=10 A-2/3,4 B-1 5/9,1 2/3 C- 2 2/3, 1 5/9 D- 4,- 2/3
Answers
Answer:
The answer should be D.
Step-by-step explanation:
You do the elimination process.
Answer:
D
Step-by-step explanation:
5x + 3y = 18 → (1)
2x - 3y = 10 → (2)
adding the 2 equations term by term will eliminate the y- term
7x + 0 = 28
7x = 28 ( divide both sides by 7 )
x = 4
substitute x = 4 into either of the 2 equations and solve for y
Substituting into (1)
5(4) + 3y = 18
20 + 3y = 18 ( subtract 20 from both sides )
3y = - 2 ( divide both sides by 3 )
y = - \(\frac{2}{3}\)
Internos consecutivos
Answers
Answer:
hi........................................
PLEASE HELP! I WILL GIVE BRAINLYEST!
Let w represent the number of weeks planting occurs at a garden that many tourists visit and let s represent
the number of seeds planted by the botanist who works for the garden.
Part A: What does the function s(w) = 15w represent in terms of the garden? What are the units of
measurement for this function? (2 points)
Part B: What does the function f(s) = 3s + 35 represent in the context of the garden? What are the units of
measurement for this function? (2 points)
Part C: What composite function represents the number of flowers the botanist can expect to bloom over a
certain number of weeks? (3 points)
Part D: Evaluate the composite function in Part C for 36 weeks. (3 points)

Answers
Part A: The function s(w) = 15w represents the number of seeds planted by the botanist as a function of the number of weeks w that planting occurs at the garden. The units of measurement for this function are seeds and weeks.
Part B: The function f(s) = 3s + 35 represents the number of flowers that can be expected to bloom as a function of the number of seeds planted by the botanist. The units of measurement for this function are flowers and seeds.
Part C: The composite function that represents the number of flowers the botanist can expect to bloom over a certain number of weeks is f(s(w)) = 3(15w) + 35 = 45w + 35.
Part D: To evaluate the composite function for 36 weeks, we substitute w = 36 into the function: f(s(36)) = 45(36) + 35 = 1635. Therefore, the botanist can expect 1635 flowers to bloom after 36 weeks of planting. The units of measurement for this answer are flowers.
1. Part A: What does the function s(w) = 15w represent in terms of the garden? What are the units of measurement for this function?
ANSWER: The function s(w) = 15w represents the total number of seeds planted by the botanist as a function of the number of weeks (w) that planting occurs at the garden. The units of measurement for this function are seeds.
2. Part B: What does the function f(s) = 3s + 35 represent in the context of the garden? What are the units of measurement for this function?
ANSWER: The function f(s) = 3s + 35 represents the total cost (in dollars) of supplies needed to plant s seeds in the garden. The units of measurement for this function are dollars.
3. Part C:What composite function represents the number of flowers the botanist can expect to bloom over a certain number of weeks?
ANSWER: the composite function that represents the number of flowers the botanist can expect to bloom over a certain number of weeks is f(s(w)) = 45w + 35.
4. Part D: Evaluate the composite function in Part C for 36 weeks.
ANSWER: the botanist can expect 1,655 flowers to bloom over 36 weeks.
If P(A) = 2/3, P(B) = 4/5 and P(AnB) = 3/5, what is P(AuB)?
Answers
Answer:
13/15
Step-by-step explanation:
P(A∪B) = P(A) + P(B) – P(A∩B)
= 2/3 + 4/5 - 3/5
Getting a common denominator
2/3 *5/5 + 4/5*3/3 - 3/5 *3/3
10/15 + 12/15 - 9/15
13/15
Answer:
\( \frac{13}{15} \)
Step-by-step explanation:
We know that,
P(AUB) = P(A) + P(B) - P(A n B)
So,
\(P(AUB) = P(A) + P(B) - P(A n B) \\ = \frac{2}{3} + \frac{4}{5} - \frac{3}{5} \\ = \frac{10 + 12 - 9}{15} \\ = \frac{22 - 9}{15} \\ = \frac{13}{15} \)
hope this helps you.
Have a nice day!
PLEASE HELPPP (algebra)

Answers
Answer:
D: 7c + 9t
Step-by-step explanation:
I assume c = car and t = truck
Since it costs 7 dollards PER car and 9 dollars PER truck, you would use 7c+9c as the equation.
what is the form of the particular solution for the given differential equation? y''-2y'-3y=4 6xe^2x
Answers
The particular solution, y''-2y'-3y=4 6xe^2x, will be in the form of (Ax^2 + Bx + C)e^(2x).
The form of the particular solution for the given differential equation, y'' - 2y' - 3y = 4(6x)e^(2x), can be found using the following steps:
Step 1: Identify the homogeneous solution
The homogeneous equation is y'' - 2y' - 3y = 0. Its characteristic equation is r^2 - 2r - 3 = 0, which factors into (r - 3)(r + 1) = 0. The roots are r1 = 3 and r2 = -1. So, the homogeneous solution is y_h(x) = C1 * e^(3x) + C2 * e^(-x).
Step 2: Determine the form of the particular solution
Since the right-hand side of the given differential equation is 4(6x)e^(2x), the form of the particular solution, y_p(x), will be a linear combination of x * e^(2x) and its derivatives. Therefore, the form of the particular solution will be:
y_p(x) = (Ax^2 + Bx + C)e^(2x), where A, B, and C are constants to be determined.
Step 3: Find the particular solution
To find the particular solution, substitute y_p(x) into the given differential equation and solve for the constants A, B, and C. Then, the particular solution, y_p(x), will be in the form of (Ax^2 + Bx + C)e^(2x).
#SPJ11
if x = 12 units and h = 8 units, then what is the area of the rhombus pictured above
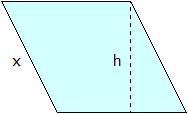
Answers
Answer:
a = 35.68 sq. units
Step-by-step explanation:
The area of a rhombus can be found by multiplying the lengths of its diagonals and dividing by 2:
Area = (diagonal 1 x diagonal 2) / 2
However, we are not given the diagonals of the rhombus. Instead, we are given that one of its sides, y, is 12 units, and its height, h, is 8 units.
Since a rhombus has four equal sides, we know that the length of the other side must also be 12 units. Therefore, the length of both diagonals of the rhombus can be found using the Pythagorean theorem:
diagonal = √(side^2 + height^2)
diagonal = √(12^2 + 8^2)
diagonal = √(144 + 64)
diagonal = √208
diagonal ≈ 14.4222 units
Now that we know the lengths of both diagonals, we can use the formula for the area of a rhombus:
Area = (diagonal 1 x diagonal 2) / 2
Area = (12 units x √208 units) / 2
Area ≈ 35.68 square units
Therefore, the area of the rhombus is approximately 35.68 square units.
Which pair of triangles can be proven congruent by SAS?.
Answers
Similar triangles may or may not be congruent.
The pair of triangles that can be proved by SAS is (a) the first pair
What is congruent triangles?
Congruence of triangles: 2 triangles are same to be congruent if all 3 corresponding sides square measure equal and every one the 3 corresponding angles square measure equal in measure.
Main body:
From the attached figures, we have the following observations
Figure 1
Two sides of both triangles are congruent
The angles between the sides are corresponding
The two congruent sides represent SS
The corresponding angles imply: SAS
This means that, the first pair of triangles are congruent by SAS postulate
Figure 2
Two angles of both triangles are congruent
The triangle share a common side
The two congruent angles represent AA
The common side imply: ASA
This means that, the second pair of triangles are congruent by ASA postulate
Figure 3 and 4
All sides of both triangles are congruent
This means that, the third and the fourth pairs of triangles are congruent by SSS postulate
Hence, the pair of triangles that can be proved by SAS is (a) the first pair
Read more about congruent triangles at:
https://brainly.com/question/3999145
#SPJ4




a company x has 34 pounds of the resource y available today. the shadow price of this resource y is us$14 per pound. the z obtained if the company implement the optimal solution is us$ 74. the upper limit of this resource y is 58 pounds. how much would be the z if the company gains access to 3 more pounds of the resource y (totalizing 37 pounds of this resource y available)?
Answers
The prize of of resource y= $14
What are equations?Equations are mathematical statements with two algebraic expressions flanking the equals (=) sign on either side.
It demonstrates the equality of the relationship between the expressions printed on the left and right sides.
We have LHS = RHS (left hand side = right hand side) in every mathematical equation.
To determine the value of an unknown variable that represents an unknown quantity, equations can be solved.
A statement is not an equation if it has no "equal to" sign.
A mathematical statement called an equation includes the sign "equal to" between two expressions with equal values.
Hence, The prize of of resource y= $14
learn more about equations click here:
brainly.com/question/2972832
#SPJ1
a ball of radius 13 has a round hole of radius 3 drilled through its center. find the volume of the resulting solid.
Answers
a ball of radius 13 has a round hole of radius 3 drilled through its center. then the volume of the resulting solid is 8.5528 x 10³ units³
The radius of the ball is 13 units.
Its volume is
V₁ = (4π*13³)/3
= 9.2028 x 10³ units³
The drilled hole has the approximate shape of a solid cylinder with radius = 3 and length = 26. Its volume is
V₂ = π*(3²)*26
= 0.650 x 10³ units³
The volume of the resulting solid is
V₁ - V₂ = 8.5528 x 10³
Answer: 8.5528 x 10³ units³
learn more about of volume here
https://brainly.com/question/4672503
#SPJ4
Addition and subtraction of algebraic expressions(9x - 1)/6 + (2x -10)/5
Answers
To solve this question, follow the steps below.
Step 01: Find the LCM of 5 and 6 (denomitators).
5, 6 | 2
5, 3 | 3
5, 1 | 5
1, 1
The LCM is 2*3*5 = 30
Step 02: Rewrite the fractions using 30 as the denominator.
To do it, divide 30 by the original denominator and multiply the result by the numerator.
\(\frac{5\cdot(9x-1)}{30}+\frac{6\cdot(2x-10)}{30}\)Step 03: Solve the expression.
First, since the fractions have the same denominator, you can write them using only one denominator:
\(\frac{5\cdot(9x-1)+6\cdot(2x-10)}{30}\)Now, remove the parentheses by solving the multiplications.
\(\begin{gathered} \frac{5\cdot9x+5\cdot(-1)+6\cdot2x+6\cdot(-10)}{30} \\ \frac{45x-5+12x-60}{30} \end{gathered}\)Adding like terms:
\(\begin{gathered} \frac{45x+12x-5-60}{30} \\ \frac{57x-65}{30} \end{gathered}\)Answer:
\(\frac{57x-65}{30}\)Using the inverse of a matrix solve the following system of equations. Give your answer as an ordered pair.

Answers
In order to solve this system using the inverse of a matrix, first let's put the system in the matrix form:
\(\begin{gathered} \begin{cases}3x+7y=-4 \\ -x-y=2\end{cases} \\ \begin{bmatrix}{3} & {7} & \\ {-1} & {-1} & {}\end{bmatrix}\cdot\begin{bmatrix}{x} \\ {y}\end{bmatrix}=\begin{bmatrix}{-4} \\ {2}\end{bmatrix} \end{gathered}\)Now the system is in the form AX = B, where A, X and B are matrices.
To solve this system, we can do the following:
\(\begin{gathered} AX=B \\ A^{-1}\cdot AX=A^{-1}\cdot B \\ X=A^{-1}\cdot B \end{gathered}\)So we need to calculate the inverse matrix of A. We can do this as follows:
\(\begin{gathered} A^{-1}=\frac{1}{|A|}\cdot_{}\begin{bmatrix}{d} & {-b} & \\ {-c} & {a} & {}\end{bmatrix} \\ A=\begin{bmatrix}{3} & {7} & \\ {-1} & {-1} & {}\end{bmatrix}\to a=3,b=7,c=-1,d=-1 \\ |A|=a\cdot d-b\cdot c=-3-(-7)=4 \\ A^{-1}=\frac{1}{4}\cdot\begin{bmatrix}{-1} & {-7} & \\ {1} & {3} & {}\end{bmatrix}=\begin{bmatrix}{-\frac{1}{4}} & {-\frac{7}{4}} & \\ {\frac{1}{4}} & {\frac{3}{4}} & {}\end{bmatrix} \end{gathered}\)Now we have:
\(\begin{gathered} X=A^{-1}\cdot B \\ \begin{bmatrix}{x} \\ {y}\end{bmatrix}=\begin{bmatrix}{-\frac{1}{4}} & {-\frac{7}{4}} & \\ {\frac{1}{4}} & {\frac{3}{4}} & {}\end{bmatrix}\cdot\begin{bmatrix}{-4} \\ {2}\end{bmatrix} \\ \begin{bmatrix}{x} \\ {y}\end{bmatrix}=\begin{bmatrix}{-\frac{1}{4}\cdot(-4)+(-\frac{7}{4})\cdot2} \\ {\frac{1}{4}\cdot(-4)+\frac{3}{4}\cdot2}\end{bmatrix}=\begin{bmatrix}{-2.5} \\ {0.5}\end{bmatrix} \end{gathered}\)So the solution of this system is x = -2.5 and y = 0.5
The following cone has a slant height of 17
cm and a radius of 8
cm.
What is the volume of the cone?
Responses
480π
320π
544π
Answers
The formula for the volume of a cone is:
V = (1/3)πr²h
where r is the radius of the base, h is the height of the cone, and π is pi.
In this case, the slant height is given as 17 cm, which we can use with the radius to find the height of the cone using the Pythagorean theorem:
h² = s² - r²
h² = 17² - 8²
h² = 225
h = 15
Now that we have the height, we can plug in the values for r and h into the formula for the volume:
V = (1/3)π(8²)(15)
V = (1/3)π(64)(15)
V = (1/3)(960π)
V = 320π
Therefore, the volume of the cone is 320π cubic cm. Answer: 320π.
Roman Derleth
Write Single Inequality from Context
Sep 21, 7:53:35 PM
?
Jonathan and his children went into a restaurant and will buy hamburgers and tacos.
Each hamburger costs $5 and each taco costs $2.50. Jonathan has a total of $60 to
spend on hamburgers and tacos. Write an inequality that would represent the
possible values for the number of hamburgers purchased, h, and the number of tacos
purchased, t.
Answer:
Submit Answer
Answers
The inequalities that represent the problem is 5h + 2.50t ≤ 60
How to find the inequality that represent the problem?Each hamburger costs $5 and each taco costs $2.50.
He has a total of $60 to spend on hamburgers and tacos.
The inequalities that would be used to represent the possible values for the number of hamburgers purchased, h, and the number of tacos purchased, t is as follows:
Therefore,
h = number of hamburgers purchased
t = the number of tacos purchased
Hence,
5h + 2.50t ≤ 60
Therefore, the inequalities that represent the problem is 5h + 2.50t ≤ 60
learn more on inequality here: https://brainly.com/question/27506356
#SPJ1
find the values of x and y. it’s a right triangle but part of it is split. the left part ugh i can’t even describe it just look at the pic

Answers
Answer:
x = 20°, y = 70° see image
Step-by-step explanation:
Use the bottom, lower, short wide triangle first. It has marks on it to show that two of the sides are the same length. That means that the opposite angles are the same. One is marked x, so the other is also x. There is a 40° angle given, along the same line right next to it has to be 140°. We'll use that one.
Also, the angles in a triangle add up to 180°.
x° + x° + 140° = 180°
See image for calculations.
Then we use the whole entire triangle. It has a 90° angle and the 20° (for x, that we just found) and y. We'll use that to find y.
90° + y + 20° = 180°
See image for calculations.

The U.S. Senate consists of 100 senators, with 2 from each of the 50 states. There are 50 Democrats in the Senate. A committee of size 10 is formed, by picking a random set of senators such that all sets of size 10 are equally likely. a) Find the expected number of Democrats on the committee. b) Find the expected number of states represented on the committee (by at least one senator) c) Find the expected number of states such that both of the state's senators are on the committee.
Answers
Note that based on probabilities,
The expected number of Democrats on the committee is 5.
The expected number of states represented on the committee is 26.
The expected number of states such that both of the state's senators are on the committee is 9.09.
How is this so ?a) The probability that a randomly chosen senator is a Democrat is 50/100 = 1/2.
So, the expected number of Democrats on a committee of size 10 is
1/2 * 10 = 5.
b) The minimum number of states that can be represented on a committee of size 10 is 2, and the maximum numberis 50.
The expected number of states representedon the committee is the average of these two values, which is (2 + 50)/ 2 = 26.
c) There are 50 states, and each state has 2 senators. So, there are a total of 100 pairs of senators.
The probability that a randomly chosen pair of senators both belong to the same state is 50/100 * 49/99
= 1/11.
The expected number of states such that both of the state's senators are on the committee is 100 * 1/11 = 9.09.
Learn more about probability at:
https://brainly.com/question/30390037
#SPJ4
Cary i checking her tax bill for the lat year. The tax rate were a follow:. No tax on the firt £11 000 of earning
Earning in exce of £11 000 and up to £43 000 taxed at a rate of 20%
Earning in exce of £43 000 and up to £150 000 taxed at a rate of 40%
Earning over £150 000 taxed at a rate of 45%
Lat year, Cary earned £45 600 before tax. How much tax did he pay in total?
Answers
If Cary earned $45600 before tax, then she paid $18240 as tax
The amount that Cary earned last year = $45600 before tax
The rate of tax if earning exceed of 43000 and up to 150000 = 40%
Then the amount of tax = The amount that Car earned last year × (The rate of tax if earning exceed of 43000 and up to 150000 / 100)
Substitute the values in the equation to find the tax amount
The amount of tax = 45600 × (40/100)
Divide the numbers first
= 45600 × 0.40
Multiply the numbers
= $18240
Hence, the amount of tax that he paid is $18240
Learn more about rate of tax here
brainly.com/question/13184546
#SPJ4