One saw and 4 hammers cost $72. Two saws and 6 hammers cost $114. How much does each item cost?
Answers
Answer: 3x-x+2=4
Step-by-step explanation:
Answer:
Step-by-step explanation:
Related Questions
A rectangle has length x and width y. Select all the statements that must
be true. (*Hint: There are 3 correct answers.) *
3 points

Answers
Answer:
I think it's the 1st box, 3rd box, and the 2nd to last box
Step-by-step explanation:
Im not really sure but hopefully its correct
What is the answer to 8(6-4n)=-27-7n
Answers
Answer:
8(6-4n) = -27-7n
8×6 8× -4n
48 -32n = -27-7n
Collect like terms
48+27 = -7n+32n
75 = 25
Divide both sides by 25
75/25 = 25/25
I need help please help me ;-;
Answers
Answer:
I think option A is correct answer
Answer:
C
Step-by-step explanation:
Option C
In square ABCD, points E and F are on sides AD and CD, respectively, such that 3DE=3FC=AB, Segments BF and CE intersect at point G. If the area of the square is 180 cm², what is the area (in cm²) of quadrilateral EDFG?
Answers
The area of quadrilateral EDFG is approximately 107.38 cm².
As 3DE = 3FC = AB, we can divide square ABCD into nine congruent smaller squares, each with an area of 20 cm² (since the total area of the square is 180 cm²). We can see that quadrilateral EDFG consists of two of these smaller squares and two right triangles.
The area of each of the smaller squares is 20 cm², so the area of both of them together is 40 cm². To find the area of the two right triangles, we need to first find the length of the diagonal of each of these squares. Using the Pythagorean theorem, we can see that the diagonal of each square is:
√(AB² + AB²) = √(2AB²) = AB√2 = 3DE√2
So the diagonal of each square is 3 times the length of DE (or FC), multiplied by the square root of 2. Since DE = FC = AB/3 = 6 cm, the diagonal of each square is:
3DE√2 = 3(6)√2 = 18√2 cm
The height of each right triangle is DE, which is 6 cm, and the base is half of the diagonal of each square, or (18√2)/2 = 9√2 cm. So the area of each right triangle is:
(1/2) × base × height = (1/2) × (9√2) × 6 = 27√2 cm²
Therefore, the area of quadrilateral EDFG is:
2 × area of small squares + 2 × area of right triangles
= 2(20 cm²) + 2(27√2 cm²)
= 40 cm² + 54√2 cm²
≈ 107.38 cm² (rounded to two decimal places)
Therefore, the area of quadrilateral EDFG is approximately 107.38 cm².
To know more about the quadrilateral visit:
https://brainly.com/question/29934440?
#SPJ1
Andrew spent 75% of his $20 allowance to go to the movies. How much did he spend? Use at least 2 strategies.
PLEASE HELP
Answers
Answer:
$15
Step-by-step explanation:
Kelly wants to fence in a rectangular space in her yard, 6 meters (length) by 10.5 meters (width). the salesperson at the supply store recommends that she put up posts every 1.5 meters. the posts cost $2.69 each. kelly will also need to buy wire mesh to string between the posts. the wire mesh is sold by the meter from large rolls and costs $5.96 a meter. a gate to fit in one of the spaces between the posts costs $25.39. seven staples are needed to attach the wire mesh to each post. staples come in boxes of 50, and each box costs $3.99. how much will the materials cost before sales tax?
Answers
The total materials cost before sales tax is $297.21.
How the total materials cost is determined:The total materials cost is the result of the addition of the total cost of posts, wire mesh, gate, and staples, as follows.
The length of the rectangular space = 6 meters
The width of the space = 10.5 meters'
The perimeter of the space = 33 meters [2(6 + 10.5)]
The space between posts = 1.5 meters
The number of posts = 22 (33 ÷ 1.5)
The cost per post = $2.69
a) The cost of the posts = $59.18 ($2.69 x 22)
The cost of wire mesh:
Cost per meter = $5.96
The number of meters of wire mesh = 33 meters
b) Total cost of the wire mesh = $196.68 ($5.96 x 33)
c) Cost of the gate = $25.39
Cost of Staples:
The number of staples per post = 7
The total number of staples required = 154 (22 x 7)
The number of boxes of staples = 4
The cost per box = $3.99
d) The total cost of staples = $15.96 (4 x $3.99)
The total cost of materials = $297.21 ($59.18 + $196.68 + $25.39 + $15.96)
Learn more about determining the total costs at https://brainly.com/question/25109150.
#SPJ4
If y=3x+4 we’re changed to y=5x+4 how would the graph of the new function compare with the first one
Answers
Answer:
t would be steeper
Step-by-step explanation:
Sigma n=0 to infinite _______
Use the binomial series to expand the function as a power series.
9/(6+x)^3
the format should be like this
Answers
The power series expansion of the function
\(9/(6+x)^3 = Sigma n=0\)to infinite \([((-1)^n * 9 * (n+2)*(n+1) / (6^(n+3))) * x^n]\)
The binomial series is given by:
(1 + x)^r = \(9/(6+x)^3 = 9(1 + ((-x)/6))^(-3)\)Sigma n=0 to infinite [(r choose n) * x^n]
where (r choose n) = \(r! / (n! * (r-n)!)\).
Using this formula, we can expand the given function \(9/(6+x)^3\) as a power series:
Let r = -3 and x = (-x/6) in the binomial series formula. Then we have:
\((1 - (x/6))^{(-3)\) = Sigma n=0 to infinite [(-3 choose n) * ((-x)/6)^n]
=\((-1)^n * (n+2)*(n+1)*x^n / (6^(n+3))\)
Therefore, we can write the power series expansion of the function as:
9/(6+x)^3 = Sigma n=0 to infinite\([((-1)^n * 9 * (n+2)*(n+1) / (6^(n+3))) * x^n]\)
Note that this power series expansion is valid for |x/6| < 1, which is equivalent to |x| < 6.
for such more questions on binomial series
https://brainly.com/question/13602562
#SPJ11
On a coordinate plane, a curved line with a minimum value of (5.1, negative 7) and a maximum value of (0, 25), crosses the x-axis at (negative 3.4, 0), (3.9, 0), and (6, 0), and crosses the y-axis at (0, 25).
Which statement is true about the local minimum of the graphed function?
Over the interval [–4, –2], the local minimum is 0.
Over the interval [–2, –1], the local minimum is 25.
Over the interval [–1, 4], the local minimum is 0.
Over the interval [4, 7], the local minimum is -7.
Answers
Answer:
D
Step-by-step explanation:
The rest of the question is the attached figure and the statement options.
A. Over the interval [–4, –2], the local minimum is 0.
B. Over the interval [–2, –1], the local minimum is 25.
C. Over the interval [–1, 4], the local minimum is 0.
D. Over the interval [4, 7], the local minimum is -7.
============================================================
According to the graph, we will check the options:
A. Over the interval [–4, –2], the local minimum is 0. (Wrong)
Because the minimum is -12
B. Over the interval [–2, –1], the local minimum is 25. (Wrong)
Because the minimum is 18
C. Over the interval [–1, 4], the local minimum is 0. (Wrong)
Because the minimum is at x = 4 less than zero
D. Over the interval [4, 7], the local minimum is -7. (True)
Answer:
The answer would be D
Step-by-step explanation:
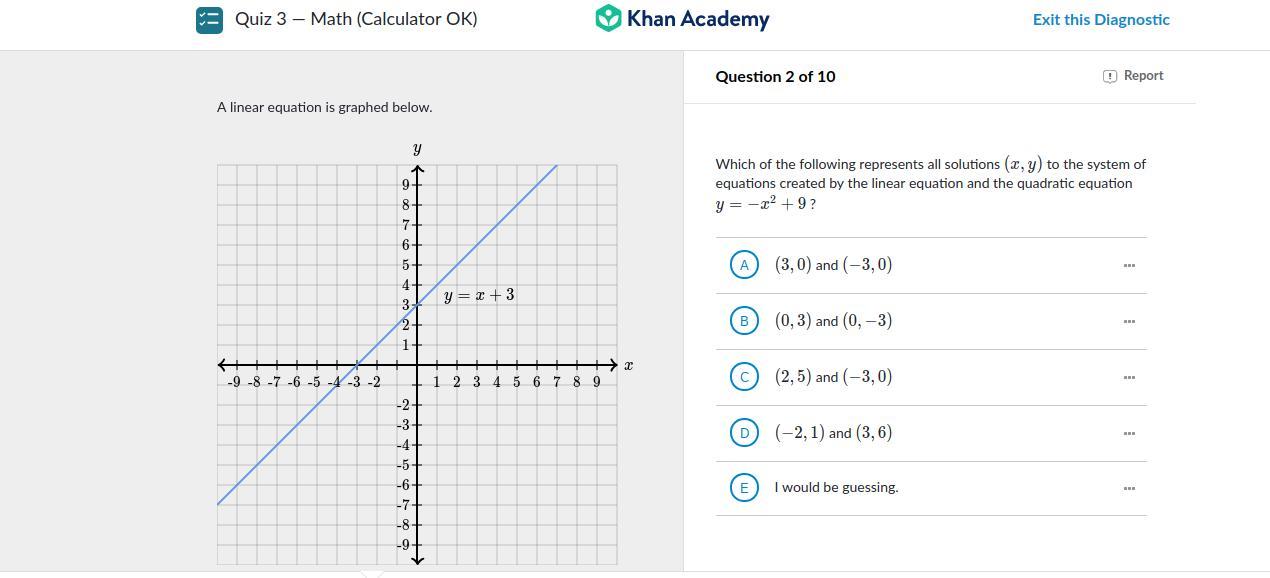
please help! i’ll give brainliest!
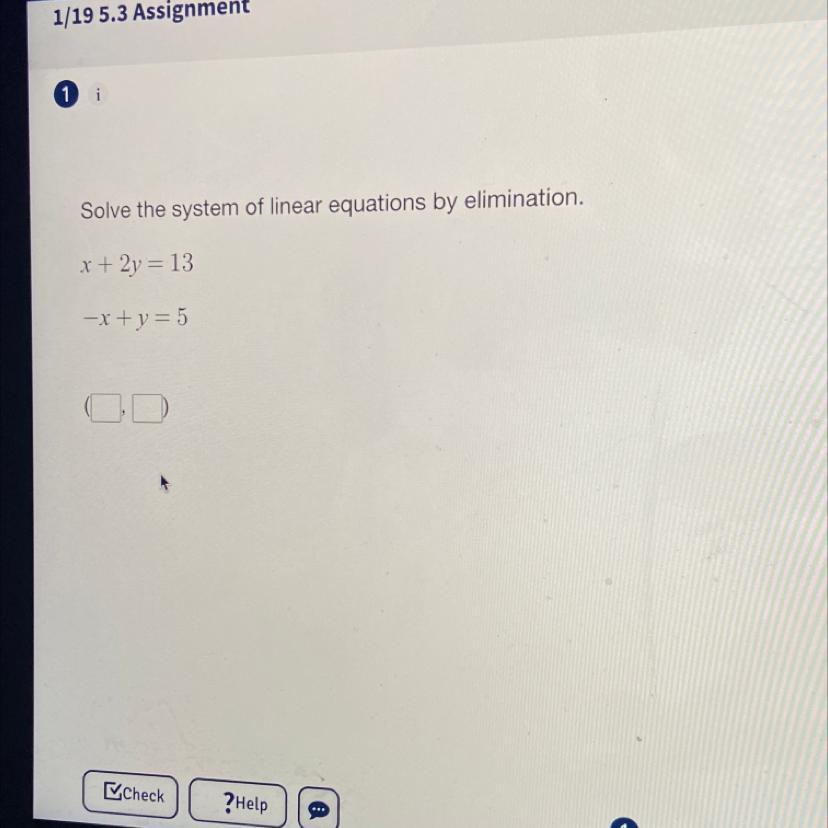
Answers
Answer:
x = 1 y = 6
Step-by-step explanation:
x + 2y = 13
-x + y = 5
3y = 18
y = 6
-x + 6 = 5
-x = -1
x = 1
How Many Solutions Does 6 + \(\frac{x}{5}\) = \(\frac{x}{5}\) - 5 - \(\frac{3x}{10}\) Have?
A. One solution
B. Two solutions
C. No solutions
D. Infinitely many solutions
Answers
Answer:
A. One solution
Step-by-step explanation:
6 + x/5 = x/5 - 5 - 3x/10
Cancel equal terms on both sides.
6=-5-3x/10
Multiply both sides of the equation by 10.
60=-50-3x
Move the variable to the left-hand side and change the sign.
60+3x=-50
Move the constant to the right-hand side and change the sign.
3x=-50-60
Calculate the difference.
3x=-110
Divide both sides by 3.
x=-110/3
=-36 2/3
Meaning one solution.
Hope this helps :)
Answer:
The answer you are looking for is A
4. Figure RST has been rotated 90 degrees clockwise to form figure OPQ.
Which of the following statements is true?
AD
O
T
is a
O meRem20
RS - PQ
O
STOP
m2S = m_P

Answers
Answer:
D
Step-by-step explanation:
i did this
The true statement is (d) m<S = m<P
How to determine the true statement?When a figure is rotated, the side lengths and the angle measures of the figure remain unchanged.
This means that:
The figure RST is congruent to the figure OPQ.
The choice of option that supports the above highlight is
m<S = m<P
Hence, the true statement is (d) m<S = m<P
Read more about rotation at:
https://brainly.com/question/4289712
Please help me !!!!!!!!!!!

Answers
Answer:
2x²+7x+3
Step-by-step explanation:
(2x+1)(x+3)
multiply the terms in the first bracket by the second bracket
2x(x+3) + 1(x+3)
=> 2x²+6x+x+3
⇒ 2x²+7x+3
Hope this helps! :)
Answer:
(2x+1)(x+3)= 2x × x + 2x × 3 + 1 × x + 1 × 3
=2x² + 6x + 1x + 3
=2x² + 7x + 3
The masses of a sheet of writing paper and an envelope are 3 g and 5 g respectively. It 60 cents to send a letter with a mass not exceeding 20 g. Albert has 60 cents worth of stamps. If x is the number of sheets of writing paper, form an inequality in x and find the maximum number of sheets of writing paper that he can use.
Answers
If the masses of a sheet of writing paper and an envelope are 3 g and 5 g respectively. The maximum number of sheets of writing paper that he can use is: 5.
How to find the maximum number of sheets ?We can start by finding the total mass of the letter and writing paper:
3x + 5 (in grams)
The maximum mass of the letter that can be sent for 60 cents is 20 g, so we can form an inequality as follows:
3x + 5 <= 20
Expanding the left-hand side:
3x + 5 <= 20
3x <= 15
x <= 5
Therefore the maximum number of sheets of writing paper that Albert can use is 5.
Learn more about maximum number of sheets here:https://brainly.com/question/12082690
#SPJ1
3. compare the results from your verification of the law of sines, cosines and tangents (make a table if possible). which law had the better results and speculate on why this might be the case?
Answers
The Law of Sines often yields better results due to its broader applicability and flexibility in solving trigonometric problems involving non-right triangles. The Law of Cosines is also reliable, especially when the lengths of sides are known. The Law of Tangents has limited use and is typically employed in specific right triangle scenarios.
To compare the results of the verification of the Law of Sines, Law of Cosines, and Law of Tangents, we can create a table showcasing the findings and analyze which law had better results:
Law | Results | Accuracy
--------------------------------------------------------------------------------------------------------------------------------------------------------
Law of Sines | Satisfied for various triangle scenarios | Dependent on angle and side accuracy
Law of Cosines | Satisfied for various triangle scenarios | Dependent on side accuracy
Law of Tangents | Satisfied for specific triangle scenarios | Dependent on angle accuracy
The Law of Sines may often have better results because it is applicable to a broader range of triangle scenarios, allowing for more flexibility in solving trigonometric problems. It is useful when working with non-right triangles, as it relates the ratios of angles to the ratios of opposite sides. However, it heavily relies on the accuracy of both angles and sides for precise calculations.
The Law of Cosines, while also effective in various triangle scenarios, is particularly useful for solving triangles when the lengths of all three sides are known or when an angle and the lengths of two sides are known. It is less dependent on angle accuracy but relies more on side accuracy.
The Law of Tangents has more limited applicability and is primarily used when dealing with right triangles. It relates the tangent of an angle to the ratios of sides, but its usage is not as widespread as the other two laws.
The Law of Sines and the Law of Cosines generally yield satisfactory results for various triangle scenarios. However, their accuracy can vary depending on the accuracy of angles and sides. The Law of Tangents, on the other hand, is more limited in its application, as it only applies to specific triangle scenarios.
To learn more about Law of Sine visit:
https://brainly.com/question/27174058
#SPJ11
find an equation for the tangent plane to the ellipsoid x2/a2 y2/b2 z2/c2 = 1 at the point p = (a/p3, b/p3, c/p3).
Answers
The equation for the tangent plane to the ellipsoid is bcp⁶x - acp⁶y - abp⁶z + acp⁶ - abcp³ = 0
Let's start by considering the ellipsoid with the equation:
(x²/a²) + (y²/b²) + (z²/c²) = 1
This equation represents a three-dimensional surface in space. Our goal is to find the equation of the tangent plane to this surface at the point P = (a/p³, b/p³, c/p³), where p is a positive constant.
The gradient of a function is a vector that points in the direction of the steepest ascent of the function at a given point. For a function of three variables, the gradient is given by:
∇f = (∂f/∂x, ∂f/∂y, ∂f/∂z)
In our case, the function f(x, y, z) is the equation of the ellipsoid: (x²/a²) + (y²/b²) + (z²/c²) = 1.
Let's compute the partial derivatives of f(x, y, z) with respect to x, y, and z:
∂f/∂x = (2x/a²) ∂f/∂y = (2y/b²) ∂f/∂z = (2z/c²)
Now, let's evaluate these partial derivatives at the point P = (a/p³, b/p³, c/p³):
∂f/∂x = (2(a/p³)/a²) = 2/(ap³) ∂f/∂y = (2(b/p³)/b²) = 2/(bp³) ∂f/∂z = (2(c/p³)/c²) = 2/(cp³)
So, the gradient of the ellipsoid function at the point P is:
∇f = (2/(ap³), 2/(bp³), 2/(cp³))
This vector is normal to the tangent plane at the point P.
Now, we need to find a point on the tangent plane. The given point P = (a/p³, b/p³, c/p³) lies on the ellipsoid surface, which means it also lies on the tangent plane. Therefore, P can serve as a point on the tangent plane.
Using the normal vector and the point on the plane, we can write the equation of the tangent plane in the point-normal form:
N · (P - Q) = 0
where N is the normal vector, P is the given point on the plane (a/p³, b/p³, c/p³), and Q is a general point on the plane (x, y, z).
Expanding the equation further, we have:
(2/(ap³))(x - (a/p³)) + (2/(bp³))(y - (b/p³)) + (2/(cp³))(z - (c/p³)) = 0
Now, let's simplify the equation:
(2/(ap³))(x - (a/p³)) + (2/(bp³))(y - (b/p³)) + (2/(cp³))(z - (c/p³)) = 0
(2(x - (a/p³)))/(ap³) + (2(y - (b/p³)))/(bp³) + (2(z - (c/p³)))/(cp³) = 0
Multiplying through by ap³ * bp³ * cp³ to clear the denominators, we obtain:
2(x - (a/p³))(bp³)(cp³) + 2(y - (b/p³))(ap³)(cp³) + 2(z - (c/p³))(ap³)(bp³) = 0
Simplifying further:
2(x - (a/p³))(bcp⁶) + 2(y - (b/p³))(acp⁶) + 2(z - (c/p³))(abp⁶) = 0
Expanding and rearranging the terms:
2bcp⁶x - 2abcp³ - 2acp⁶y + 2abcp³ - 2abp⁶z + 2acp⁶ = 0
Simplifying:
bcp⁶x - acp⁶y - abp⁶z + acp⁶ - abcp³ = 0
Finally, we can write the equation of the tangent plane to the ellipsoid at the point P = (a/p³, b/p³, c/p³) as:
bcp⁶x - acp⁶y - abp⁶z + acp⁶ - abcp³ = 0
This equation represents the tangent plane to the ellipsoid at the given point.
To know more about tangent plane here
https://brainly.com/question/32190844
#SPJ4
student researchers wanted to see whether a short delay between seeing a list of words and when people were asked to recall them would hinder memorization. the subjects were shown a list of words to memorize for 1 minute and were then given 1 minute to recall as many words as they could. each subject did this once with no delay between memorizing and recall and another time with a 30-second wait between memorizing and recall. they were randomly assigned the order of the two conditions. the number of words memorized under each condition can be found in the statcrunch data set memorizingwords. questions: use the appropriate simulation applet to calculate an approximate p-value. is there strong evidence that a short delay hinders the memorization process? explain.
Answers
The appropriate simulation applet to calculate an approximate p-value is 0.0077.
The strong evidence that a short delay hinders the memorization process is strong data suggests that a brief delay impairs memorization.
Delay or no delay, answer: the number of words remembered
The mean distance between words remembered with and without delay over time is null, or zero.
Alt: The mean distance in words remembered over the long term (with no delay minus with delay) is higher than 0.
Yes, the majority of the lines do skew to the right. The mean for no delay is 10.55 whereas that for with delay is 8.7.
The mean distance in words remembered is 1.85.
1)0.0077 as the p-value
2)Strong data suggests that a brief delay impairs memorization.
For more such question on impairs.
https://brainly.com/question/14691128
#SPJ4
20. There is a sale on shoes of 15% off. My wife buys three pairs of
shoes, one for $120, one for $95, and one for $105. What is her total
sale price for all three pairs?
Answers
Answer:
48$
Step-by-step explanation:
120×15=1,800
1,800÷100=18$
95×15=1,425
1,425÷100=14.25$
105×15=1,575
1,575÷100=15.75$
18+14.25+15.75=48
Max and bob went to McDonald’s. Max bought 2 burgers and 2 drinks for five dollars. Bob Bought 3 burgers and 1 drink for $5.50. How much is each burger and drink?
Answers
Answer:
A burger is 1.50 and a drink is 1.50.
Step-by-step explanation:
Max´s: So 2 burgers would cost 1.50 so ( for the 2 drinks) 1.50 + 1.50 is 2.50 and 1.50 and 1.50 is 2.50 add the 2 2.50s you get 5.00
Bob: Bob gets 3 burgers which is 1.50 times 3 is 4.50 + 1.50 for one drink the answer would be 5.50
Hope that helps!
Of all rectangles with area 256, which one has the minimum perimeter? Let P and w be the perimeter and width, respectively, of the rectangle. Write the objective function in terms of P and w. Assume that the width is less than the length if the dimensions are unequal.
Answers
Thus, the rectangle with the minimum perimeter among all rectangles with an area of 256 has dimensions 16 x 16, and the perimeter is 64.
To find the rectangle with the minimum perimeter among all rectangles with an area of 256, we need to use optimization techniques. Let's assume the length of the rectangle is L, then the area can be expressed as Lw=256, where w is the width. The perimeter P can be expressed as P=2(L+w).
Now, we can write the objective function in terms of P and w as follows:
P = 2(L + w)
= 2(L + 256/L)
To find the minimum value of P, we need to take the derivative of P with respect to L and set it equal to zero:
dP/dL = 2 - 512/L^2 = 0
Solving this equation gives us L=16. Therefore, the width of the rectangle is w=256/L=16.
In conclusion, to find the rectangle with the minimum perimeter among all rectangles with area 256, we can use optimization techniques and the objective function P=2(L + w). The minimum perimeter occurs when the length and width are both 16, and the perimeter is 64. This solution is obtained by setting the derivative of the objective function with respect to the length equal to zero.
To know more about rectangles visit:
https://brainly.com/question/29123947
#SPJ11
A ship is travelling at a heading of 220 ∘
at a speed of 14 knots. A current is flowing at a speed of knots, at a bearing of 060 ∘
. What is the ship's ground speed?
Answers
The ship's ground speed is approximately 14.1 knots.
Given that:
A ship is traveling at a heading of 220∘ at a speed of 14 knots.
A current is flowing at a speed of knots, at a bearing of 060∘.To determine the ship's ground speed, we have to use the vector addition method.
Using the sine and cosine rules, the following triangle can be solved:
Let S be the ship's speed and D be the direction it is heading in.
Let C be the current's speed and B be the direction it is flowing in.
Using the sine rule, we can determine the angle A:
Since A + B + C = 180,
angle B is 60 and
angle C is
180 - 60 - A
= 120 - A.
Ground speed: 14.1 knots (rounded to one decimal place).
Know more about the vector addition
https://brainly.com/question/2927458
#SPJ11
What is the equation of the Y axis?
Answers
Answer:
x=0
Step-by-step explanation:
The general form of the equation of y-axis is x = 0. hence, the equation of line parallel to the y-axis is given by the equation: x = k.
what type of sampling is used when it is not possible to select individuals directly from the target population?
Answers
Answer:
If a researcher cannot gain access to a target population, snowball sampling procedures can assist in locating subjects. In regard to sampling procedures, if a researcher wants to be able to generalize results to the total population of interest, then a purposeful sampling technique is the best approach.
Answer:
Non-probability sampling
Step-by-step explanation:
Non-probability sampling is a method of selecting units from a population using a subjective method.
Solve the equation. 6+6 sin0=4 cos ²0 What is the solution in the interval 050
Answers
Given the equation: \(6 + 6sin θ = 4 cos²\) θIn the interval \(0 < θ < 50\), we need to solve for the value of θ.To solve the given equation, we will use the trigonometric identity: \(1 - sin² θ = cos² θ\)
Therefore, 4cos² θ can be written as: \(4(1 - sin² θ) = 4 - 4sin² θ\)
Now substituting \(4cos² θ = 4 - 4sin² θ\) in the given equation, we get:\(6 + 6sin θ = 4 - 4sin² θ\)
Rearranging the equation, we get:\(4sin² θ + 6sin θ - 2 = 0\)
Solving the above quadratic equation for sin θ, we get:\(sin θ = [-6 ± √(6² - 4 x 4 x -2)]/8sin θ = [-6 ± √52]/8sin θ = [-3 ± √13]/4\)
Hence, we will take the positive value of sin θ,\(sin θ = [-3 + √13]/4sin θ ≈ 0.282\)
Now, using sin θ = 0.282, we can find the value of cos θ as:\(cos θ = √(1 - sin² θ)cos θ = √(1 - 0.282²)cos θ ≈ 0.959\)
Thus, the solution of the given equation in the interval \(0 < θ < 50 is:θ ≈ 16.5° or θ ≈ 33.5°.\)
To know more about interval visit:
https://brainly.com/question/11051767
#SPJ11
sara bought 36 ounces of cheese for 3.24 what was the unit price of cheese
Answers
Answer:
$0.09
Step-by-step explanation:
Unit price= total price/ total units
$3.24/ 36oz= $0.09
Answer:
$0.09
Step-by-step explanation:
i just used my homework for this so i don't really know how to explain it cause i just had my answer there.
( 3.24 / 36 = $0.09 )
solve for x
103.5
4.7
55.0

Answers
Answer:
It will be the first one
Step-by-step explanation:
Hope this Helped

Determine whether the series is convergent or divergent. 3^(n+1)4^-n If it is convergent, find its sum.
Answers
Geometric series is convergent if the |r|<1 where r is the common ratio.
Let Sn=∑ni=0(−3/4)i then
Sn=(−3/4)n+1−1(−3/4)−1
Now take n→∞ then
Sn→0−1(−3/4)−1=4/7
because |−3/4|<1 and so (−3/4)n→0. Now note that your sum is
lim ∑i=1n+1(−3)i−14i=lim 14∑i=1n+1(−3)i−14i−1=1/4.lim Sn=1/7.
Geometric series: A geometric series is the result of adding together geometric sequences indefinitely. Depending on the sequence given to us, such infinite sums can either be finite or infinite. A series is considered to be convergent if the partial sums gravitate to a certain value, also known as a limit. In contrast, a divergent series is one whose partial sums do not reach a limit. Divergent series frequently reach, reach, or avoid a particular number.
know more about geometric series here
https://brainly.com/question/4617980#
#SPJ4
I suck at geometry and guess what my homework is on. Supposed to find the perimeter of the triangle on the left and the area of the figure to the right of the triangle.

Answers
Answer:
Perimeter = 85.5cm, Area = 3163.5cm
Step-by-step explanation:
To find the perimeter of a shape, you need to add all of the sides together.
In this case, you need to add 3 sides together.
38cm + 37cm + x.
To find x, you need to subtract 81.1 from 98.7 and divide by two. (98.7 - x - x = 81.1)
(98.7 - 81.1) / 2 = 8.8.
The perimeter is: 8.8cm + 38cm + 29cm = 85.5cm
To find the area of the trapezoid (shape on the right of the triangle), you need to use the formula, (length of top + length of bottom)/2 * height.
Length of the top base: 81.1cm
Length of bottom base: 98.7 - 8.8 = 89.9cm
Height = 37
(81.1 + 89.9) / 2 * 37 = 3163.5cm
What is the area of a circle with a radius of 10 inches? use 3. 14 for pi. 31. 4 in² 62. 8 in² 314 in² 628 in².
Answers
Work Shown:
A = pi*r^2
A = 3.14 * 10^2
A = 3.14 * 100
A = 314 square inches
This value is approximate since pi = 3.14 is approximate.
The area of the circle is :
↬ 314 in²Work:
To calculate the circle's area, I will use the formula
\(\sf{C=\pi r^2}\)
whereC = circumferenceπ = 3.14r = radius (10 inches)Diagram:
\(\setlength{\unitlength}{1.1cm}\begin{picture}(0,0)\thicklines\qbezier(2.3,0)(2.121,2.121)(0,2.3)\qbezier(-2.3,0)(-2.121,2.121)(0,2.3)\qbezier(-2.3,0)(-2.121,-2.121)(0,-2.3)\qbezier(2.3,0)(2.121,-2.121)(-0,-2.3)\put(0,0){\line(1,0){2.3}}\put(0.5,0.3){\bf\large 10\ inches}\end{picture}\)
Plug in the values :
\(\begin{gathered}\sf{A=3.14\times10^2}\\\\\sf{A=3.14\times100}\\\\\boxed{\boxed{\bf{A=314\:in^2}}}\end{gathered}\)
Hence, the circle's area is 314 in².Let u = 26 [ 4 -2] and A= -5 9 . Is u in the plane in R3 spanned by the columns of A? Why or why not? 1 1 Select the correct choice below and fill in the answer box to complete your choice. (Type an integer or decimal for each matrix element.) O A. Yes, multiplying A by the vector writes u as a linear combination of the columns of A. O B. No, the reduced row echelon form of the augmented matrix is , which is an inconsistent system
Answers
No, u is not in the plane spanned by the columns of A.
To check if u is in the plane spanned by the columns of A, we first need to construct the augmented matrix of the system A · x = u, where x is the vector of unknowns. The augmented matrix is:
[−5 9 | 26 4 −2]
The reduced row echelon form of this augmented matrix is:
[1 0 | 2 -1]
This is an inconsistent system,the reduced row echelon form of the augmented matrix is , which is an inconsistent system so it does not have any solutions. This means that u cannot be written as a linear combination of the columns of A, so it is not in the plane spanned by the columns of A.
Learn more about augmented matrix here:
https://brainly.com/question/16796667
#SPJ4