On Babylonian tablet YBC 4652, a problem is given that translates to this equation:
X + + x plus StartFraction x Over 7 EndFraction plus StartFraction 1 Over 11 EndFraction left-parenthesis x plus StartFraction x Over 7 EndFraction right-parenthesis equals 60.(x + ) = 60
What is the solution to the equation?
x = 48.125
x = 52.5
x = 60.125
x = 77
Answers
The solution to the equation is x = 48.125.
To solve the equation represented by the Babylonian tablet YBC 4652, let's break down the given equation and solve for x.
The equation is:
x + (x + x/7 + 1/11)(x + x/7) = 60
We'll simplify it step by step:
First, distribute the terms:
x + (x + x/7 + 1/11)(x + x/7) = 60
x + (x^2 + (2x/7) + (1/11)(x) + (1/7)(x/7)) = 60
x + (x^2 + (2x/7) + (x/11) + (1/49)x) = 60
Combine like terms:
x + x^2 + (2x/7) + (x/11) + (1/49)x = 60
Next, find a common denominator and add the fractions:
(49x + 7x^2 + 22x + 4x + x^2) / (49*7) = 60
(7x^2 + x^2 + 49x + 22x + 4x) / 343 = 60
8x^2 + 75x / 343 = 60
Now, multiply both sides by 343 to get rid of the denominator:
8x^2 + 75x = 343 * 60
8x^2 + 75x = 20580
Rearrange the equation in standard quadratic form:
8x^2 + 75x - 20580 = 0
To solve this quadratic equation, we can either factor it or use the quadratic formula. Factoring may not be easy, so let's use the quadratic formula:
x = (-b ± √(b^2 - 4ac)) / (2a)
Plugging in the values:
x = (-75 ± √(75^2 - 4 * 8 * -20580)) / (2 * 8)
x = (-75 ± √(5625 + 662400)) / 16
x = (-75 ± √667025) / 16
Now, calculate the square root and simplify:
x = (-75 ± 817.35) / 16
x = (-75 + 817.35) / 16 or x = (-75 - 817.35) / 16
x = 742.35 / 16 or x = -892.35 / 16
x ≈ 48.125 or x ≈ -55.772
Since the value of x cannot be negative in this context, the approximate solution to the equation is:
x ≈ 48.125
For more such questions on solution,click on
https://brainly.com/question/24644930
#SPJ8
Answer:
The correct answer is A. X= 48.125
Step-by-step explanation:
Related Questions
What are some of the reasons that the values of p and for the class might differ from the same frequencies reported for the North American population? Check all that apply. a) The class data is based on a small population of individuals. b) Natural selection is occurring in the population for PTC tasters. c) Migration of individuals from other parts of the world may be affecting the gene pool. d) Random mutations affect the alleles of PTC tasters at different rates for those in the class. Mating selection occurs for those who cannot taste PTC.
Answers
The values of p and for the class might differ from the same frequencies reported for the North American population due to a variety of reasons. Some of these reasons include:
a) The class data is based on a small population of individuals. This can lead to sampling bias and can result in inaccurate representation of the larger population.
b) Natural selection is occurring in the population for PTC tasters. This can result in certain alleles becoming more or less prevalent in the population over time, leading to a difference in the frequencies of PTC tasters in the class and the larger population.
c) Migration of individuals from other parts of the world may be affecting the gene pool. This can introduce new alleles into the population and change the frequencies of PTC tasters.
d) Random mutations affect the alleles of PTC tasters at different rates for those in the class. This can result in changes in the frequencies of PTC tasters over time.
e) Mating selection occurs for those who cannot taste PTC. This can lead to a change in the frequencies of PTC tasters in the population over time.
Overall, there are a variety of reasons why the values of p and for the class might differ from the same frequencies reported for the North American population. These reasons include sampling bias, natural selection, migration, random mutations, and mating selection.
To know more about sampling bias click on below link:
https://brainly.com/question/29611745#
#SPJ11
Answer:
The answer is A and C
A The class data is based on a small population of individuals
C Migration of individuals from other parts of the world may be affecting the gene pool.
Step-by-step explanation:
If x+4/4 = y+7/7 then x/4 =___.
(Number 9 is the one I need an answer for)
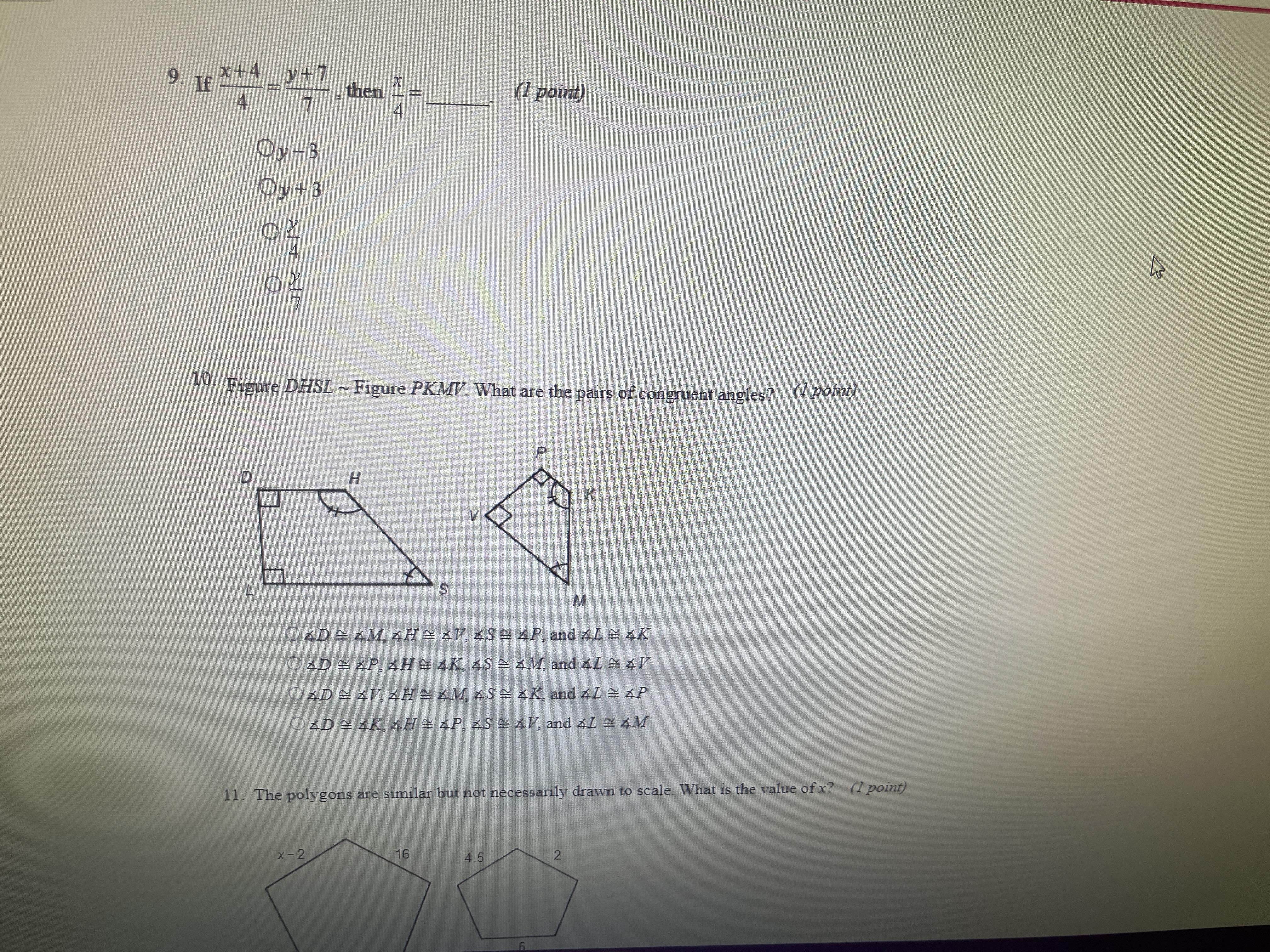
Answers
Answer:
4th answer is correct
Step-by-step explanation:
First, let us make x the subject.
\(\sf \frac{x+4}{4} =\frac{y+7}{7}\)
Use cross multiplication.
\(\sf 7(x+4)=4(y+7)\)
Solve the brackets.
\(\sf 7x+28=4y+28\)
Subtract 28 from both sides.
\(\sf 7x=4y+28-28\\\\\sf7x=4y\)
Divide both sides by 7.
\(\sf x=\frac{4y}{7}\)
Now let us find the value of x/4.
To find that, replace x with (4y/7).
Let us find it now.
\(\sf \frac{x}{4} =\frac{\frac{4y}{7} }{4} \\\\\sf \frac{x}{4} =\frac{4y}{7}*\frac{1}{4} \\\\\sf \frac{x}{4} =\frac{4y}{28}\\\\\sf \frac{x}{4} =\frac{y}{7}\)
What is the slope and y-intercept of the line graphed below?

Answers
Answer:
Slope is 2 and the y-intercept is 2
Step-by-step explanation:
Answer:
slope=2
y-intercept=2
Step-by-step explanation:
i did rise over run and got 4/2=2
y-intercept is when the line hits a number on the y axis which in this case is (0,2)
hope this helps :) have a nice day !!
please let me know if this was wrong
Claire keeps track of the miles per gallon her car gets per week. She has accumulated the following data: (1, 22.42), (2, 22.84), (3, 23.26), (4, 23.68) What is the common difference or ratio
Answers
The common difference is 0.42. The comparison of each ratio's successive values over time for a single firm.
Now, According to the question:
What is meant by ratio?
When expressed in numbers or amounts, a ratio is a relationship between two things. For example, if a room contains ten boys and thirty girls, the boy-to-girl ratio is 1:3, or one to three.A ratio, or getting rationed, on the occurs when replies to a tweet vastly outnumber likes or retweets. This means that people are reacting negatively to the tweet's content.It usually means that your comment has received more replies than likes. This implies that there are more people who disagree with your comment than agree with it.Therefore, simplifying the equation then we get,
if you take the ranges (y) and subtract one from the other you get 0.42.
(22.84 - 22.42)/(2 - 1) = 0.42/1 = 0.42
(23.26 - 22.84)/(3 - 2) = 0.42
(23.68 - 23.26)/(4 - 3) = 0.42
Hence, The common difference is 0.42
Learn more about Ratio at:
https://brainly.com/question/13419413
#SPJ4
Bart can type 296 words in 8 minutes. What is his unit rate
Answers
Answer:
37
Step-by-step explanation:
296 ÷ 8 = 37
Sorry I couldn't explain more, but I hope this helps!
Answer:
The unit rate is 37 words per minute.
Step-by-step explanation:
296 divided by 8 is 37
Question 7: 1 pts Consider the function f(x) = x2 - 8x + 50. The slope of the tangent line at x = 5 is 2. Find the equation of this tangent line e - (Write your answer in the form y=mx+b with no space
Answers
Simplifying, we get: y - 35 = 2x - 10 or y = 2x + 25 Hence, the equation of the tangent line is y = 2x + 25.
Given that the function is f(x) = x2 - 8x + 50. The slope of the tangent line at x = 5 is 2. To find the equation of the tangent line, we need to find the y-coordinate of the point on the curve at x = 5.
We can do that by plugging x = 5 into the given function:
f(5) = 5² - 8(5) + 50
= 25 - 40 + 50
= 35.
So the point on the curve at x = 5 is (5, 35).
We can use the point-slope form of the equation of a line to find the equation of the tangent line:
y - y₁ = m(x - x₁)
where (x₁, y₁) is the point on the curve at x = 5 and m is the slope of the tangent line, which we are given is 2.
Substituting the values, we get: y - 35 = 2(x - 5)`Simplifying, we get: y - 35 = 2x - 10 or y = 2x + 25
Hence, the equation of the tangent line is y = 2x + 25.
To know more about equation of the tangent line Visit:
https://brainly.com/question/6617153
#SPJ11
A map Uses a scale of — centimeter = 75 kilometers.
50 kilometers
Answers
Answer:
Step-by-step explanation:
75
Pls help idk what to put and pls explain
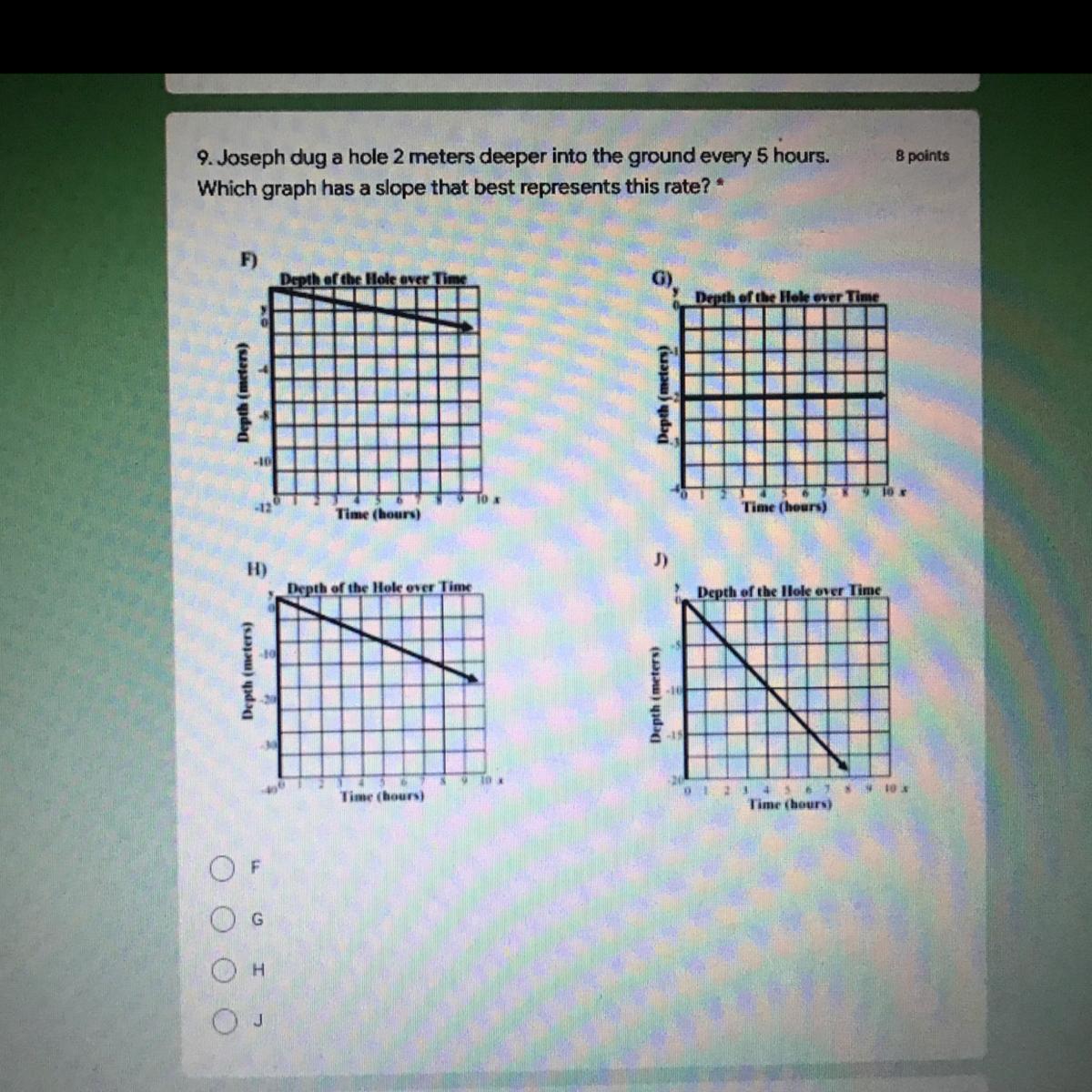
Answers
There is a box of colored marbles on the counter top. There are 24 blue, 16 green, and 6 red. What is the ratio of red to blue marbles? SIMPLIFY, if possible.
Answers
Answer:
24:6
Step-by-step explanation:
SOMEBODY PLEASE HELP ME!
9*__=33?

Answers
Answer:
11/3
Step-by-step explanation:
Step 1:
Start by setting it up with the divisor 33 on the left side and the dividend 9 on the right side like this:
3 3 ⟌ 9
Step 2:
The divisor (33) goes into the first digit of the dividend (9), 0 time(s). Therefore, put 0 on top:
0
3 3 ⟌ 9
Step 3:
Multiply the divisor by the result in the previous step (33 x 0 = 0) and write that answer below the dividend.
0
3 3 ⟌ 9
0
Step 4:
Subtract the result in the previous step from the first digit of the dividend (9 - 0 = 9) and write the answer below.
0
3 3 ⟌ 9
- 0
9
You are done.
The answer is the top number and the remainder is the bottom number.
Therefore, the answer to 9 divided by 33 calculated using Long Division is:
0
9 Remainder
What is the value of the expression below?
−23 ⋅ 5−6
Question 1 options:
−45
−59
59
45
Answers
Answer:
b
Step-by-step explanation:
Robin has a collection of dimes, nickels and quarters. He has 4 times as many dimes as nickels. He has 20 more quarters than nickels. The
ratio of the number of dimes to the number of quarters is 3:2. Which equation can be used to calculate the number of nickels, n, Robin
has?
OA
Exh
8:33
acer

Answers
Answer: Robin has 50 nickels, 60 dimes, and 120 quarters.
Step-by-step explanation:
A plane takes off and climbs at a 10º angle. After flying over 12 miles of ground, what will the plane's altitude, h, be? Round to the nearest tenth of a mile.
Answers
=========================================================
Explanation:
A diagram is optional, but I find it helps sometimes. The diagram is shown below.
Opposite the 10 degree angle is h. So we consider h the opposite side.
The hypotenuse is 12. The hypotenuse is always opposite the 90 degree angle.
Apply the sine ratio to solve for h
sin(angle) = opposite/hypotenuse
sin(10) = h/12
12*sin(10) = h
h = 12*sin(10)
h = 2.08377813200317 which is approximate
h = 2.1 miles is the plane's altitude which is also approximate
Side note: 2.1 miles is equal to 11,088 feet (multiply by 5280 to convert from miles to feet).

use a graph to estimate the values of x such that ex > 1,000,000,000. (round your answer to three decimal places.) a) Use a graph to estimate the values of x such that ex > 100,000. (Round your answer to three decimal places.) x >b) Find the exponential function f(x) = Cbx whose graph is given. f(x) =
Answers
The answer is that the value of x such that ex > 1,000,000,000 is x > 14.876 (rounded to three decimal places) and the exponential function f(x) = Cbx whose graph is given is f(x) = 25000e0.03x.
a) To estimate the value of x such that ex > 1,000,000,000, we can use a graph of the exponential function ex. On the graph, we can locate the point (x, ex) = (14.876, 1,000,000,000), which means that when x = 14.876, ex > 1,000,000,000. Therefore, the value of x such that ex > 1,000,000,000 is x > 14.876 (rounded to three decimal places).
b) The exponential function f(x) = Cbx whose graph is given is f(x) = 25000e0.03x.
The answer is that the value of x such that ex > 1,000,000,000 is x > 14.876 (rounded to three decimal places) and the exponential function f(x) = Cbx whose graph is given is f(x) = 25000e0.03x.
The complete question is :
Use a graph to estimate the values of x such that ex > 1,000,000,000. (round your answer to three decimal places.) a) Use a graph to estimate the values of x such that ex > 100,000. (Round your answer to three decimal places.) x >b) Find the exponential function f(x) = Cbx whose graph is given. f(x) = 25000e0.03x.
learn more about function here
https://brainly.com/question/12431044
#SPJ4
Vw¯¯¯¯¯¯¯¯¯=40 in. the radius of the circle is 25 inches. find the length of ct¯¯¯¯¯¯¯.
Answers
The value of the length of SP is 15 inches. So option C is true.
Used the concept of Pythagoras's theorem that states,
The well-known geometric theorem is that the sum of the squares on the legs of a right triangle is equal to the square on the hypotenuse.
Given that,
VW = 40
VG = 20
ST = 20
and, PT=25
Now, using Pythagoras's theorem
\(ST^2+SP^2=PT^2\)
Substitute the given values,
\(20^2+SP^2=25\)
\(400+SP^2=625\)
Subtract 400 on both sides,
\(PS^2 = 225\)
Taking square root on both sides,
\(SP=15\text{ inches }\)
Therefore, the length of SP is 15 inches. So, option C is true.
Learn more about Pythagoras's theorem here:
brainly.com/question/343682
#SPJ12
The complete question is shown in the image.

99 times the sum of v and 9

Answers
Answer:
Step-by-step explanation:
99(v + 9) is all you need here.
Estimate the value of the irrational number (0.6289731...)2. Up to how many decimal digits is the estimation correct? PLS Help
Answers
Answer:
5
Step-by-step explanation:
Now we will look at two famous irrational numbers, and e and calculate their approximate decimal expansions. As you may remember, pi is used in geometry and has been around for over 4000 years. It is used to find area of a circle, surface area and volume of a sphere, cone, and cylinder. Its value is used in many real world calculations such as mechanics, architecture, nature, art, and even medicine. The value e is called Euler’s number and is very important in exponential functions such as finance. Let’s approximate the value of these two numbers, e and .
Example 5:
To determine the decimal expansion of , we will use the fact that the number is the area of a unit circle together with counting the total squares inside a circle on a grid. Remember, . The unit circle is a circle with a radius of 1. Since the area of a unit circle is equal to and we will be counting squares, we can decrease our work by focusing on the area of just of the circle. Take a look at the illustrations below to help you understand our premise.
Unit Circle Area using grids
A = (1)2
A = Area of circle = total number of squares inside circle
Let’s take a look at of the unit circle using a 10 x 10 grid. It is difficult to count the number of squares inside the quarter circle because some are not whole squares.
We have inner squares inside the quarter circle, and outer squares outside of the quarter circle. Next, we mark a border inside the circle and outside the circle, as close as possible to the circle. The inside border should enclose all the whole squares inside the quarter circle, (red). The outside border contains all the whole squares within the quarter circle and parts of the squares that are outside the circle (black). Now let’s estimate the area of the unit circle to approximate .
Let r2 equal all inner squares and s2 equal all the squares within the black border and quarter circle. There are 69 inner squares and 89 inner and outer squares. Algebraically, r2 < < s2.
If we consider the area of the square with side length equal to 10 squares of the grid paper, then the area of r2 = and area of s2 = .
Therefore,
r2 < < s2
We know this is accurate because 2.76 < 3.14 < 3.44. Of course we can improve our estimate of by including more of the partial grid squares inside the quarter circle. By combining the partial squares there appears to be about 7 more inside the circle. We then add 7 to the 69. This gives us,
We can reason the same way as before to estimate s2 to 80, instead 86.
We are getting closer to approximating pi. Suppose we divide each square horizontally and vertically instead of having 100 squares, we have 400 squares.
Multiplying by 4 throughout, we have
By looking at partial squares we can estimate r2 = 310 and s2 is 321. Then, the inequality is
We can continue the process to get closer and closer estimates,
3.14159 < < 3.14160
and then continue on to get an even more precise estimate of . By now, we have a very close one already.
We conclude by making one final observation about and irrational numbers. When we take the square of an irrational number such as , we are doing so without knowing the exact value of . Since we can use a calculator to show that 3.14159 < < 3.14160, we also know
3.141592 < < 3.141602
9.8695877281 < < 9.86965056
Notice that the first 4 digits, 9.869 are the same on both sides of the inequality. Therefore, we can say that ^2=9.869 is correct to 3 decimal digits.
Example 6:
Estimate the value of the irrational number (12.03801...)2
Solution:
The estimated value is 144.91 and correct up to 2 decimal digits.
To estimate this, we truncate to one digit higher for the number on the right. Then we square.
12.038012 < (12.03801...)2 < 12.038022
144.91585161 < (12.30791)2 < 144.91825924
The first two decimal places are the same, therefore (12.03801...)2 = 144.91 is correct up to 2 decimal digits.
Example 7:
Estimate the value of the irrational number (9.204107...)2
Solution:
The estimated value is 84.715, which is correct up to 3 decimal digits.
9.2041072 < (9.204107...)2 < 9.2041082
84.715585667449 < (9.204107...)2 < 84.715604075664
(9.204107...)2 = 84.715 is correct up to 3 decimal digits.
Answer:
it is 6 dude
Step-by-step explanation:
The length of a rectangle i 2cm greater than the width of the rectangle. The perimeter of the rectangle i 24cm
Answers
The length of the rectangle is 7 cm and the width is 5 cm.
Perimeter of a rectangle:The whole distance covered by the rectangle's borders or its sides is known as its perimeter. As we know the rectangle will have 4 sides then the perimeter of the rectangle will be equal to the total of its four sides. And the unit will be in meters, centimeters, inches, feet, etc.
The formula for the Perimeter of the rectangle is given by
Perimeter = 2( Length + Width )Here we have
The length of a rectangle is 2cm greater than the width of the rectangle
And perimeter of the rectangle = 24 cm
Let x be the width of the rectangle
From the given data,
Length of the rectangle = (x + 2) cm
As we know Perimeter of rectangle = 2(Length+width)
=> Perimeter of rectangle = 2(x+2 + x) = 2(2x +2)
From the given data,
Perimeter of rectangle = 24cm
=> 2(2x +2) = 24 cm
=> (2x +2) = 12 [ Divided by 2 into both sides ]
=> 2x = 12 - 2
=> 2x = 10
=> x = 5 [ divided by 2 into both sides ]
Length of rectangle, (x+2) = 5 + 2 = 7 cm
Therefore,
The length of the rectangle is 7 cm and the width is 5 cm.
Learn more about Perimeter of a rectangle at
https://brainly.com/question/29595517
#SPJ4
Graph a parabola whose vertex is at (3,5)(3,5)left parenthesis, 3, comma, 5, right parenthesis with yyy-intercept at y=1y=1y, equals, 1.
Answers
Using the given information we found that the equation of the parabola is:
y = (-4/9)*(x - 3)^2 + 5
And its graph is below.
How to get the equation of the parabola?
For a parabola with vertex (h, k), the equation is:
y = a*(x - h)^2 + k
Here the vertex is (3, 5), so the equation is:
y = a*(x - 3)^2 + 5
And the y-intercept is y = 1, this means that:
1 = a*(0 - 3)^2 + 5
1 = a*9 + 5
1 - 5 = a*9
-4/9 = a
So the parabola is:
y = (-4/9)*(x - 3)^2 + 5
And its graph is below.
If you want to learn more about parabolas, you can read:
https://brainly.com/question/1480401

1. In an experiment to determine the bacterial communities in an aquatic environment, different samples will be taken for each possible configuration of: type of water (salt water or fresh water), season of the year (winter, spring, summer, autumn), environment (urban or rural). If two samples are to be taken for each possible configuration, how many samples are to be taken? 2. An academic senate has 15 members. A special committee of 5 members will be formed. In how many different ways can the committee be formed? 3. Suppose the academic senate is composed of 10 faculty representatives and 5 ex- officio members. The special committee must contain 4 faculty representatives and 1 ex-officio member. In how many different ways can the committee be formed?
Answers
If two samples are to be taken for each possible configuration, then 32 samples are to be taken. And 3003 are the number of ways in which the committee can be formed. Also, there are 1050 different ways the committee can be formed with 4 faculty representatives and 1 ex-officio member.
1. To determine the bacterial communities in the aquatic environment with different configurations, you need to consider the number of options for each configuration and multiply them together.
- Type of water: 2 options (salt water or fresh water)
- Season of the year: 4 options (winter, spring, summer, autumn)
- Environment: 2 options (urban or rural)
To calculate the total number of samples, you multiply the options for each configuration:
2 (type of water) × 4 (season of the year) × 2 (environment) = 16
Since you are taking two samples for each configuration, you multiply the total number of samples by 2:
16 (total configurations) × 2 (samples per configuration) = 32 samples to be taken.
Therefore, you need to take a total of 32 samples.
2. To calculate the number of different ways the special committee of 5 members can be formed from the academic senate of 15 members, you need to use the combination formula.
The number of ways to choose 5 members out of 15 is given by the combination formula:
C(15, 5) = 15! / (5! × (15 - 5)!) = 3003
Therefore, there are 3003 different ways the committee can be formed.
3. In this case, the special committee must have 4 faculty representatives and 1 ex-officio member. We can calculate the number of ways to choose 4 faculty representatives from the 10 available and 1 ex-officio member from the 5 available.
The number of ways to choose 4 faculty representatives out of 10 is given by the combination formula:
C(10, 4) = 10! / (4! × (10 - 4)!) = 210
The number of ways to choose 1 ex-officio member out of 5 is simply 5.
To calculate the total number of ways the committee can be formed, we multiply these two numbers together:
210 (faculty representatives) × 5 (ex-officio members) = 1050
Therefore, there are 1050 different ways the committee can be formed with 4 faculty representatives and 1 ex-officio member.
To learn more about sample: https://brainly.com/question/24466382
#SPJ11
"Jerry would like to have $85,000 for a down payment on a new
house. Jerry plans to buy the house in 9 years. How much would
Jerry have to deposit today into a savings account paying 8%
interest in ord"
Answers
The present value, or the amount Jerry would need to deposit today, is approximately $47,120.23.
To calculate the amount Jerry would need to deposit today, we can use the formula for present value:
Present Value = Future Value / (1 + Interest Rate)ⁿ
Where:
Future Value is $85,000
Interest Rate is 8% (or 0.08 as a decimal)
n is the number of years, which is 9
Plugging in these values into the formula, we have:
Present Value = $85,000 / (1 + 0.08)⁹
Simplifying the expression:
Present Value = $85,000 / (1.08)⁹
Calculating this expression using a calculator or spreadsheet software, we find that the present value, or the amount Jerry would need to deposit today, is approximately $47,120.23.
To know more about present value:
https://brainly.com/question/29140663
#SPJ4
suppose Tom's preferences can be represented using the utility function is U(x,y) = 24xy. what must the value of b in the function W(x,y) = 160 x^b y^68 such that function W also represents Tom's preferences?
Answers
Tom's preferences, the value of b in the function W(x, y) = 160xᵇ y⁶⁸ should be greater than 1.
A utility function is a mathematical representation used in economics to quantify the preferences or satisfaction a consumer derives from consuming different goods or bundles of goods. It assigns a numerical value, known as utility, to each possible combination of goods or services, reflecting the consumer's preferences.
The utility function is typically denoted as U(x1, x2, ..., xn), where x1, x2, ..., xn represent the quantities of different goods or services consumed. The utility function maps the combination of goods to a real number, indicating the level of satisfaction or utility the consumer derives from that combination.
Utility functions can take different functional forms, depending on the assumptions and models used. Common types include linear utility functions, Cobb-Douglas utility functions, and logarithmic utility functions. These functions capture different patterns of preferences and allow economists to analyze various economic phenomena, such as consumer demand, welfare analysis, and decision-making under uncertainty.
To represent Tom's preferences, the utility function U(x, y) = 24xy is given.
We need to find the value of b in the function W(x, y) = 160x^b y^68 such that it also represents Tom's preferences.
To match Tom's preferences, the two utility functions, U(x, y) and W(x, y), should have the same ranking of preferences. In other words, if U(x1, y1) > U(x2, y2), then W(x1, y1) should also be greater than W(x2, y2).
Let's compare the utility values for two sets of goods (x1, y1) and (x2, y2) using the given utility function U(x, y) = 24xy:
U(x1, y1) = 24x1y1
U(x2, y2) = 24x2y2
For the function W(x, y) = 160xᵇ y⁶⁸, we need to determine the value of b such that W(x1, y1) > W(x2, y2) whenever U(x1, y1) > U(x2, y2).
Comparing the utility values, we have:
24x1y1 > 24x2y2
To maintain the same ranking of preferences, we can equate the corresponding W values:
160x1 y1⁶⁸ > 160x2 y2⁶⁸
Now, canceling out the common factors, we get:
x1ᵇ y1⁶⁸ > x2ᵇ y2ᵇ^68
Since this should hold for any x1, y1, x2, y2, we can compare the exponents of x and y separately:
b > 1
To represent Tom's preferences, the value of b in the function W(x, y) = 160x^b y^68 should be greater than 1.
To know more about function visit:
https://brainly.com/question/16798149
#SPJ11
A regular polygon has exterior angles of 60°
What is the sum of the polygon’s interior angles?
Answers
Answer:
720°
Step-by-step explanation:
The sum of the exterior angles of a polygon = 360°
Divide by 60 to find number of sides (n)
n = 360° ÷ 60° = 6
The sum of the interior angles of a polygon is
sum = 180° (n - 2) ← n is the number of sides
Here n = 6 , then
sum = 180° × 4 = 720°
The sum of the exterior angles of a regular polygon is 360º
Each exterior angle of a regular polygon is 60º/n
360º/n=60º
360/60=n
6=n
A polygon with 6 sides is a hexagon.
Use the formula (n-2)×180
(6-2)*180=4*180=720º
another solution...
you have 6 interior angles (hexagon)
if an exterior angle is 60º, the corresponding interior angle is 180-60=120º
you have 6 of these 120º angles
6*120=720º
Which equation represents the relationship between the angles in the figure?
х
х
75°
x + 75 = 90
2x + 75-90
x + 75 - 180
2x + 75 = 180

Answers
Answer:
D. 2x+75=180Step-by-step explanation:
Given:
This figure gives us 180 degrees of angles.
Calculate the angle of x in the figures according to the term x on one side of the equation.
The angle relationship should be represented by 2x.
2x+75=180
First, subtract by 75 from both sides.
2x+75-75=180-75
Solve.
Subtract the numbers from left to right.
180-75=105
2x=105
Divide by 2 from both sides.
2x/2=105/2
Solve.
Divide the numbers from left to right.
105/2=52.5
x=105/2=52.5
Therefore, the correct answer is "D. 2x+75=180".I hope this helps. Let me know if you have any questions.
Given f(x) and g(x) = k⋅f(x), use the graph to determine the value of k.
a
−5
b
negative one fifth
c
one fifth
d
5
Help please.

Answers
Answer:
(a) -5
Step-by-step explanation:
The vertical scale factor for the graph and the function can be found by comparing the y-value of a point on f(x) to the y-value of a point on g(x). The graph conveniently marks two corresponding points with these y-values:
f(-2) = 2
g(-2) = -10
The value of k in g(x)=k·f(x) is the ratio of these y-values:
k = g(-2)/f(-2) = -10/2 = -5
The value of the vertical scale factor k is -5.
what is the term to term rule for this sequence 64 32 16 8 4
Answers
Answer:
Divide by 2 each time.
Step-by-step explanation:
The rule is dividing by 2 each time.
64/2=32
32/2=16
16/2=8
8/2=4
Hope this helps you!! Have an amazing day, and happy thanksgiving ^^
The puppy shelter where Clara works is moving to a new building. The rooms in the new building are built to hold 6 puppies each. Clara needs to figure out how many rooms she'll need to house a total of 78 puppies.
Use an equation to find the number of rooms Clara needs.
Answers
Answer:
Equation: 6x = 78Rooms: 13Step-by-step explanation:
Let the number of rooms is x.
Each room is built to hold 6 puppies, so x rooms hold 6x puppies.
The equation for this is:
6x = 78x = 78/6x = 13And the solution is 13 rooms.
A rectangle has a length that is 3 times its width. If the perimeter of the rectangle is 20 in, what is the area?
Answers
Given
length = 3 times width
Let w = width, and l = 3w
Then the perimeter is
2l + 2w = 20 in
2(3w) + 2w = 20 in
6w + 2w = 20 in
8w = 20 in
w = 2.5 in
l = 3w
l = 3(2.5 in)
l = 7.5 in
Now that we have length and the width, we can now solve for area.
\(\begin{gathered} A=lw \\ A=(7.5\text{ in})(2.5\text{ in}) \\ A=18.75\text{ in}^2 \end{gathered}\)Therefore, the area of the rectangle 18.75 square inches.
Find 10(-3)(4) - (-15)
Answers
The expression is simplified to -105
What is an integer?An integer can be defined as a whole number, with no fractional or decimal form which can be positive, negative or zero.
Negative integer values are the additive inverses of their corresponding positive numbers.
Integers are a collection of whole numbers and negative values.
The types of integers are;
Positive integersNegative integersZeroFrom the information given, we have;
10(-3)(4) - (-15)
expand the bracket
10(-12) - ( -15)
expand further
-120 + 15
Add the values
-105
Hence, the value is -105
Learn more about integers here:
https://brainly.com/question/929808
#SPJ1
Factorise a2 -10a-24
Answers
Answer:
(a+2)(a-12)
Step-by-step explanation:
\(a^2-10a-24\\\\\mathrm{Break\:the\:expression\:into\:groups}\\=\left(a^2+2a\right)+\left(-12a-24\right)\\\\\mathrm{Factor\:out\:}a\mathrm{\:from\:}a^2+2a\mathrm{:\quad }a\left(a+2\right)\\\\\mathrm{Factor\:out\:}-12\mathrm{\:from\:}-12a-24\mathrm{\\:\quad }-12\left(a+2\right)\\=a\left(a+2\right)-12\left(a+2\right)\\\\\mathrm{Factor\:out\:common\:term\:}a+2\\=\left(a+2\right)\left(a-12\right)\)
Answer:
(a + 2)(a - 12)
Step-by-step explanation:
a^2 - 10a - 24
using splitting method
a^2 - 12a + 2a - 24
taking separate common from both pairs
a(a - 12) + 2(a - 12)
(a + 2)(a - 12)