On a map where each unit represents 100 miles, two airports are located at P(1,17) and Q(12,10). What is the distance, to the nearest whole mile, between the two airports? A. 1,800 miles B. 1,304 miles C. 1,122 miles D. 900 miles
Answers
Using the distance formula, the distance, to the nearest whole mile, between the two airports is: B. 1,304 miles.
How to Apply the Distance Formula?The distance formula is: d = \(\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\).
Given the following locations:
P(1,17) = (x1, y1)
Q(12,10) = (x2, y2)
Use the distance formula to find the PQ:
PQ = √[(12−1)² + (10−17)²]
PQ = √[(11)² + (−7)²]
PQ = √170
PQ ≈ 13.04 units
1 unit = 100 miles
PQ = 13.04 × 100
PQ = 1,304 mils
Thus, using the distance formula, the distance, to the nearest whole mile, between the two airports is: B. 1,304 miles.
Learn more about the distance formula on:
https://brainly.com/question/661229
#SPJ1
Answer: B. 1,304 miles.
Related Questions
For the given matrix A find a 3x2 matrix B such that AB=I, where I is the 2x2 identity matrix. [Hint: If B1 and B2 are the columns of B, then ABj = Ij.]A =1 2 11 1 1
Answers
We can solve this equation by setting B2 = [c d], so that AB2 = [c+d 1] = [0 1]. This gives us the system of equations c + d = 0 and c = 1. Solving this system, we have c = 1, where I is the 2x2 identity matrix
Let A be the given 2x2 matrix A = [1 2 ; 1 1]. To find a 3x2 matrix B such that AB = I, where I is the 2x2 identity matrix, we can use the hint provided: If B1 and B2 are the columns of B, then ABj = Ij. This means that for each column j of B, we need to solve the equation ABj = Ij. For j = 1, we have AB1 = I1 = [1 0]. We can solve this equation by setting B1 = [a b], so that AB1 = [a+b 1] = [1 0]. This gives us the system of equations a + b = 1 and a = 0. Solving this system, we have a = 0 and b = 1, so B1 = [0 1].For j = 2, we have AB2 = I2 = [0 1]. We can solve this equation by setting B2 = [c d], so that AB2 = [c+d 1] = [0 1]. This gives us the system of equations c + d = 0 and c = 1. Solving this system, we have c = 1.
Learn more about identity matrix here:
https://brainly.com/question/28177340
#SPJ4
There are 18 girls in a class.
If this is 40% of the class list, how many students are in the class?
Answers
Answer:
45 students
Step-by-step explanation:
40+40=80 40/2=20 80+20=100
18+18=36 18/2=9 36+9=45
horrible explaining but hope it helps :)
Answer:
45
Step-by-step explanation:
18 ÷ 45 = 0.4 = 40%
The cost of 5 kg of mangoes is rupees 147. At what rate per kg are the mangoes
being sold.
Answers
Step-by-step explanation:
the cost of 1 kg mangoes = 147/ 5
= Rs. 29.40
mark me as brainliest
Answer:
cost of 1 kg mango = rupees 29.4
Step-by-step explanation:
cost of 5 kg mangoes =rupees 147
cost of 1 kg mango =?
Now, lets find cost of 1 kg mangoes
CP od 1 kg mangoes = cost of 5 kg mangoes/5 kg
=rupees 147/5
=rupees 29.4
what are the factors to 424,380
Answers
Answer:
the factors are: 1, 2, 3, 4, 5, 6, 10, 11, 12, 15, 20, 22, 30, 33, 44, 55, 60, 66, 110, 132, 165, 220, 330, 643, 660, 1286, 1929, 2572, 3215, 3858, 6430, 7073, 7716, 9645, 12860, 14146, 19290, 21219, 28292, 35365, 38580, 42438, 70730, 84876, 106095, 141460, 212190, 424380.
Step-by-step explanation:
What is (9.3x10^34) in scientific notation?
(3.1x 10^17)

Answers
Answer:
B
Step-by-step explanation:
3 x 10 ^17
Which is B
edit: So when doing scientific notation, you just divide the important first number of 9.3 or whatever by 3.1 like normal.
Then, when doing exponents, heres a rule of thumb.
When adding exponents, the base must be the same.
9.3 ^ 100 + 9.3 ^ 3 = 9.3 ^103
9.3 ^ 29 + 4.4 ^ 54 = cannot be solved
When subtracting exponents, the same rule applies as adding, the bases must be the same, otherwise, you just subtract or add like normal.
When dividing exponents, you just subtract exponents. The bases must be the same though of course.
3 ^ 30
----------
3 ^ 20
==== 3 ^ 10
When multiplying exponents, you add exponents like normal. Bases are the same ect.
4 ^ 49 x 4 ^ 2 = 4 ^ 51
When doing scientific notation, the same rule applies.
The 10 is the base, so in your case, you divide the 9.3 and 3.1 like normal to get 3.
The exponent by the 10 is subtracted to get 17 since 34 - 17 = 17.
25^x-1=5^2x-1 -100\(25^x-1=5^2x-1 -100\)
Answers
Answer: x=2.
Step-by-step explanation:
\(\displaystyle \\25^{x-1}=5^{2x-1}-100\\\\(5^2)^{x-1}=\frac{5^{2x}}{5} -100\\\\5^{2*(x-1)}=\frac{5^{2x}}{5} -100\\\\5^{2x-2}=\frac{5^{2x}}{5}-100\\\\\frac{5^{2x}}{5^2} =\frac{5^{2x}}{5} -100\\\\\frac{5^{2x}}{25} =\frac{5^{2x}}{5} -100\ |*25\\\\5^{2x}=5*5^{2x}-2500\\\\5^{2x}+2500=5*5^{2x}-2500+2500\\\\5^{2x}+2500=5*5^{2x}\\\\5^{2x}+2500-5^{2x}=5*5^{2x}-5^{2x}\\\\2500=4*5^{2x}\ |:4\\\\625=5^{2x}\\\\5^4=5^{2x}\ \ \ \ \ \ \Rightarrow\\\\4=2x\ |:2\\\\2=x\\\\Hence\ \ x=2.\)
Find value of X please

Answers
Answer:
x=7
Step-by-step explanation:
Step #1- Set the two lines equal to each other
10+12=x+15
Step #2- Solve for the line you have all values for
10+12=22
Step#3- Plug 22 back into the equation where the two lines are set equal to each other
22=x+15
Step #4- Solve for X algebraically
22=x+15
22-15=x
7=x
HELP ME WITH THIS IMPROPER FRACTION QUESTION pls

Answers
Answer:
(a) \(4\frac{1}{5}\)
(b) \(7\frac{7}{24}\)
Step-by-step explanation:
One way of operating with mixed numbers is to first convert them into improper fractions, and operate with them following the simple rules of fraction multiplication, and at the end convert the answer into mixed number.
(a) For this operation let's first convert \(5\,\frac{2}{5}\) into an improper fraction:
\(5\frac{2}{5} =5+\frac{2}{5} =\frac{25}{5} +\frac{2}{5} =\frac{27}{5}\)
Now perform the requested operation:
\(\frac{7}{9} \,*\,\frac{27}{5} =\frac{189}{45} =\frac{21}{5} =4\frac{1}{5}\)
(b) Start by converting both mixed numbers into improper fractions and then operate as indicated:
\(1\frac{3}{4} =\frac{4+3}{4} =\frac{7}{4} \\4\frac{1}{6} =\frac{24+1}{6} =\frac{25}{6}\)
\(\frac{7}{4} *\frac{25}{6} =\frac{175}{24} =7\frac{7}{24}\)
guys please help this is a math question
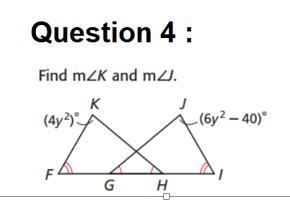
Answers
Answer:
81.5
Step-by-step explanation:
<G and <H are congruent
<F and <I are congruent
so the last two angles in both triangles must also be congruent
this means that <K and <J are congruent
so we can create this equation: <K = <J
substitute the angles with what we know: 4\(y^{2}\) = 6\(y^{2}\) - 40
add 40 to both sides and subtract 4\(y^{2}\) from both sides: 40 = 2\(y^{2}\)
you get: 20 = \(y^{2}\)
root square on both sides: \(\sqrt{20}\) = \(\sqrt{y^{2} }\)
you get: y ≈ 4.5
substitute this into one of the equations for a missing variable:
6\(y^{2}\) -----> 6 (4.5 x 4.5) - 40
6 ( 20.25) - 40
121.5 - 40
81.5
A foreign country uses the stellar as its currency. Before a trip to that country, Jon wants to exchange $1,500 to stellars. Which of Bank A and Bank B has the better exchange rate? How many more stellars would he get if he exchanged his $1,500 at the better exchange rate instead of at the other rate?
Answers
Answer:
Bank A will exchange it
Step-by-step example
hi I need help on my homework plz help
Answers
PERSEVERE For the cube, x represents a positive whole number. Find the value for x such that the volume of the cube and 6 times the area of one of its faces have the same value.
Answers
The value of x if the volume and 6 by the area of one face are equal is 6
How to determine the value of x?The side length of the cube is given as
Side length = x
From the question, we have the statement to be
The volume of the cube and 6 times the area of one of its faces have the same value.
The volume of a cube with side length x is
V = x³
The surface area multiplied by 6 is
A = 6x²
When both have the same values, we have
x³ = 6x²
Divide both sides by x²
x = 6
Hence, the value of x is 6
Read more about volume at
https://brainly.com/question/463363
#SPJ1
Jeffrey caught 8 worms in his backyard. 4 worms had a length of 3 inches. The other 4 worms were all the same size. The total length of all the worms combined is 32 inches. Which equation below represents the lengths of all the worms?
A 4x + 3x = 324x + 3x = 32
B 4(x + 3) = 324(x + 3) = 32
C 4x + 3 = 324x + 3 = 32
D 3(x + 4) = 32
Answers
Option (B) 4 ( x + 3 ) = 32 is the equation that represents the lengths of all the worms.
We are given that:
Jeffrey has 8 worms
The 4 worms in it has the length of 3 inches.
The expression would become:
Length = 4 × 3
Also, we are given that the rest 4 worms are of equal length.
Let that equal length be x
The expression becomes:
Length = 4 × x = 4 x
Also, we are given that the total length of the worms = 32 inches.
The equation becomes:
32 = 3 × 4 + 4 × x
4 ( x + 3 ) = 32
Therefore, option (B) 4 ( x + 3 ) = 32 is the equation that represents the lengths of all the worms.
Learn more about equation here:
https://brainly.com/question/1214333
#SPJ9
need the help asap!!!

Answers
Step-by-step explanation:
ur awnser is b!
Five candy bars cost 3.23.how much will 7 candy bars cost
Answers
Answer:
3.23/5=.646
.646*7=4.522
rounded is $4.52
Step-by-step explanation:
A runner is running a 10 km race. It takes her 17.5 minutes to reach the 2.5 km mark. at that rate, how long would it take her to run the whole race?
Answers
Answer:
time = 70 minutes
Prove how they are congruent. Geometry:SSS

Answers
\(\huge \bf༆ Answer ༄\)
For the given triangles to be congruent by SSS criterion, the sides HJ and LN should be equal ~
therefore correct choice is ~ C
\( \large \boxed{ \sf \: HJ \cong LN}\)
The additional information needed to prove that both triangles are congruent by the SSS Congruence Theorem would be: C. HJ ≅ LN
Recall:
Based on the Side-Side-Side Congruence Theorem, (SSS), two triangles can be said to be congruent to each other if they have three pairs of congruent sides.Thus, in the two triangles given, the two triangles has:
Two pairs of congruent sides - HI ≅ ML and IJ ≅ MNTherefore, an additional information needed to prove that both triangles are congruent by the SSS Congruence Theorem would be: C. HJ ≅ LN
Learn more about SSS Congruence Theorem on:
https://brainly.com/question/4280133
What is the exact perimeter of the trapezoid?

Answers
but the answer rounded to the nearest thousandth is 54.806

Find the Dy/Dx of y=7/x using first principle
Answers
By using first principle, the value of Dy/Dx is,
⇒ Dy/Dx = - 7 / x²
What is an expression?Mathematical expression is defined as the collection of the numbers variables and functions by using operations like addition, subtraction, multiplication, and division.
We have to given that;
The expression is,
⇒ y = 7 / x
Now, Differentiate the function with respect to x, we get;
⇒ y = 7 / x
⇒ Dy/ Dx = D / Dx (7 / x)
= 7 D/Dx (1/x)
= 7 (- 1 × x⁻¹⁻¹ )
= 7 (- x⁻²)
= - 7 / x²
⇒ Dy/Dx = - 7 / x²
Learn more about the mathematical expression visit:
brainly.com/question/1859113
#SPJ1
A company makes wax candles in the shape of a cylinder. Each candle has a diameter of 6 inches and a height of 4 inches. How much wax will the company need to make 140 candles?
Use 3.14 for \(\pi\) , and do not round your answer.
Answers
Answer:
The company will need 3,360 inches of wax
Step-by-step explanation:
To find how much wax you need per one candle you would do 6in.X4in. which gives you 24in. of wax. Then to find the amount of was for 140 candles you would do 140X24in. to get 3,360 inches of wax.
find the centroid of the region bounded by the given curves. y=12x,y=√x
Answers
The centroid of the region bounded by the curves y = 12x and y = √x is (72,1.88).
To find the centroid of the region bounded by the given curves y = 12x and y = √x, the following steps should be followed.
Step 1: Sketch the region bounded by the two curves to have an idea of what the region looks like.
Step 2: Determine the area of the region bounded by the two curves. The area A can be computed by evaluating the definite integral of the difference between the two functions. \(\[\int\limits_{0}^{144} (\sqrt{x}-12x)dx\]\) We solve for this integral below.\(\[\int\limits_{0}^{144} (\sqrt{x}-12x)dx = 64 - 1728 + \frac{2}{3}\sqrt{6}\] \[\int\limits_{0}^{144} (\sqrt{x}-12x)dx = -1663.30\]\)
Step 3: To find the centroid of the region, we need to determine the x and y coordinates of the centroid. The x-coordinate of the centroid is given by the formula below.
\(\[x = \frac{1}{A}\int\limits_{a}^{b} \frac{1}{2}(y_1^2-y_2^2)dx\]\)
where A is the area of the region, and y1 and y2 are the upper and lower functions, respectively. Substituting values, we obtain
\(\[x = \frac{1}{-1663.30}\int\limits_{0}^{144} \frac{1}{2}((\sqrt{x})^2-(12x)^2)dx\] \[x = 72\]\)
The y-coordinate of the centroid is given by the formula below.
\(\[y = \frac{1}{2A}\int\limits_{a}^{b}(y_1+y_2)\sqrt{(y_1-y_2)^2+4dx}\]\)
Substituting values, we obtain \(\[y = \frac{1}{2(-1663.30)}\int\limits_{0}^{144}(12x+\sqrt{x})\sqrt{(\sqrt{x}-12x)^2+4dx}\] \[y = 1.88\]\)
For more such questions on centroid
https://brainly.com/question/7644338
#SPJ11
Verify [cos(x)/1+sin(x)] - [cos(x)/1-sin(x)] = -2tan(x)
Answers
Answer:
L.H.S = R. H.S
Step-by-step explanation:
Hope, you see the image .
Note; Way to solve question may vary according to your grade
This process is for grade 9 and above
For lower level you can express all tri.. ratios in p , b & h and prove it
![Verify [cos(x)/1+sin(x)] - [cos(x)/1-sin(x)] = -2tan(x)](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/PhJE7MdrOaJy7JdXzCxux0ugu5uXYPF0.jpeg)
Determine whether the series is convergent or divergent. 3^(n+1)4^-n If it is convergent, find its sum.
Answers
Geometric series is convergent if the |r|<1 where r is the common ratio.
Let Sn=∑ni=0(−3/4)i then
Sn=(−3/4)n+1−1(−3/4)−1
Now take n→∞ then
Sn→0−1(−3/4)−1=4/7
because |−3/4|<1 and so (−3/4)n→0. Now note that your sum is
lim ∑i=1n+1(−3)i−14i=lim 14∑i=1n+1(−3)i−14i−1=1/4.lim Sn=1/7.
Geometric series: A geometric series is the result of adding together geometric sequences indefinitely. Depending on the sequence given to us, such infinite sums can either be finite or infinite. A series is considered to be convergent if the partial sums gravitate to a certain value, also known as a limit. In contrast, a divergent series is one whose partial sums do not reach a limit. Divergent series frequently reach, reach, or avoid a particular number.
know more about geometric series here
https://brainly.com/question/4617980#
#SPJ4
Use the triangle below to find the following trig ratios. Express your answer as a fraction.
a) sin
b) cos
c) tan

Answers
Answer:
Step-by-step explanation:
First we need the length of the hypotenuse.
20^2 + 21^2 = c^2
400 + 441 = c^2
841 = c^2
29 = c
If you are using angle B as your theta (angle from which the relations are formed:
a) sin = O/H = 20/29
b) cos = A/H = 21/29
c) tan = O/A = 20/21
Please help me!!! This is due in an hour!!!

Answers
You would multiply 12 x 5 then divide that by 2
10 pts
Remy is considering moving into a one-bedroom apartment in Quiet Trees Gardens. The apartment has
a monthly rent of $1,650.
Below are the fees she has been quoted. How much is she expected to pay up front in order to rent this
apartment?
Application: 1.5% of 1 month's rent
Credit application fee $30
Security deposit: 1 month's rent
Last month's rent
Broker's fee: 7% of 1 year's rent
$6,390.75
$6,820.35
O $3,090,75
$4,740,75
Question 4
10 pts
Answers
Answer:
Total amount pay for new apartment = $4,740.75
Step-by-step explanation:
Find:
Total amount pay for new apartment
Computation:
Particular Amount
Monthly rent of apartment $1,650
Add:
Application fee [1,650 x 1.5%] $24.75
Credit application fee $30
Security rent $1,650
Broker's fee [1,650 x 12 x 7%] $1,386
Total $4,740.75
Total amount pay for new apartment = $4,740.75
original price $18 and percent of discount is 65% what is the sale price
Answers
Answer:
$6.3
Step-by-step explanation:
Original price = $18
Percentage Discount = 65%
Discount = 18*65% = 18*0.65 = $11.7
Sale Price = Original price - Discount
= $18 - $11.7
= $6.3
help on math homework

Answers
Answer:
b can I have
Step-by-step explanation:
Which is an equation of the line with a slope of 1/4 and a
y-intercept of - 2?
a. x-4y=8
b. x+4y=-8
c. 4x+y=-2
d. 4x-y=2
Answers
Answer:
x-4y=8
Step-by-step explanation:
x-4y=8
-4y=-x+8
y =-x/4 + 2
For a particle in a box of length L, what is the probability the particle will exist between x=0 and x=L/3, if the quantum number n=3.
Answers
The probability for the particle to exist between x=0 and x=L/3, when the quantum number n=3, is 1/9.
In quantum mechanics, a particle in a one-dimensional box of length L can only occupy certain discrete energy levels determined by the quantum number n. The energy levels are given by the equation En = (\(n^2\) * \(h^2\))/(8m\(L^2\)), where h is Planck's constant and m is the mass of the particle.
Given that the quantum number n = 3, we can determine the energy associated with this level as E3 = (\(3^2\) * \(h^2\))/(8m\(L^2\)).
The probability of finding the particle between x=0 and x=L/3 corresponds to the portion of the total probability density function (PDF) within that range. The PDF for a particle in a box is given by P(x) = |ψ\((x)|^2\), where ψ(x) is the wave function.
For the ground state (n = 1), the wave function is a sin(xπ/L) and the corresponding PDF is proportional to \(sin^2\)(xπ/L). For n = 3, the wave function becomes sin(3xπ/L), and the corresponding PDF is proportional to\(sin^2\)(3xπ/L).
To find the probability, we integrate the PDF from x=0 to x=L/3, which is equivalent to calculating the area under the PDF curve within that range. In this case, the integral is ∫[0 to L/3] \(sin^2\)(3xπ/L) dx.
Evaluating this integral gives us a result of 1/9, indicating that there is a 1/9 probability of finding the particle between x=0 and x=L/3 when the quantum number n=3.
Learn more about Quantum number
brainly.com/question/32773003
#SPJ11