On a map, 1 inch equals 20 miles. Two cities are 6 inches apart on the map. What is the actual distance between the cities?
Answers
Answer:
idk
Step-by-step explanation:
idk just responding
for points
Answer:
120 miles
Step-by-step explanation:
If 1 inch = 20 miles, you can multiply both sides by 6 to figure out how many miles 6 inches represent.
Related Questions
NEED HELP ASAP!!! MARK BRAINLLEST IF ITS CORRECT
NO LINKS!!!!!!!!!!!!

Answers
-177147x^28
Hope this helps lol
These two triangles are similar. What is the length of side a and b? Help ASAP pleasee! Look at the screenshot Please, Thank you! :)
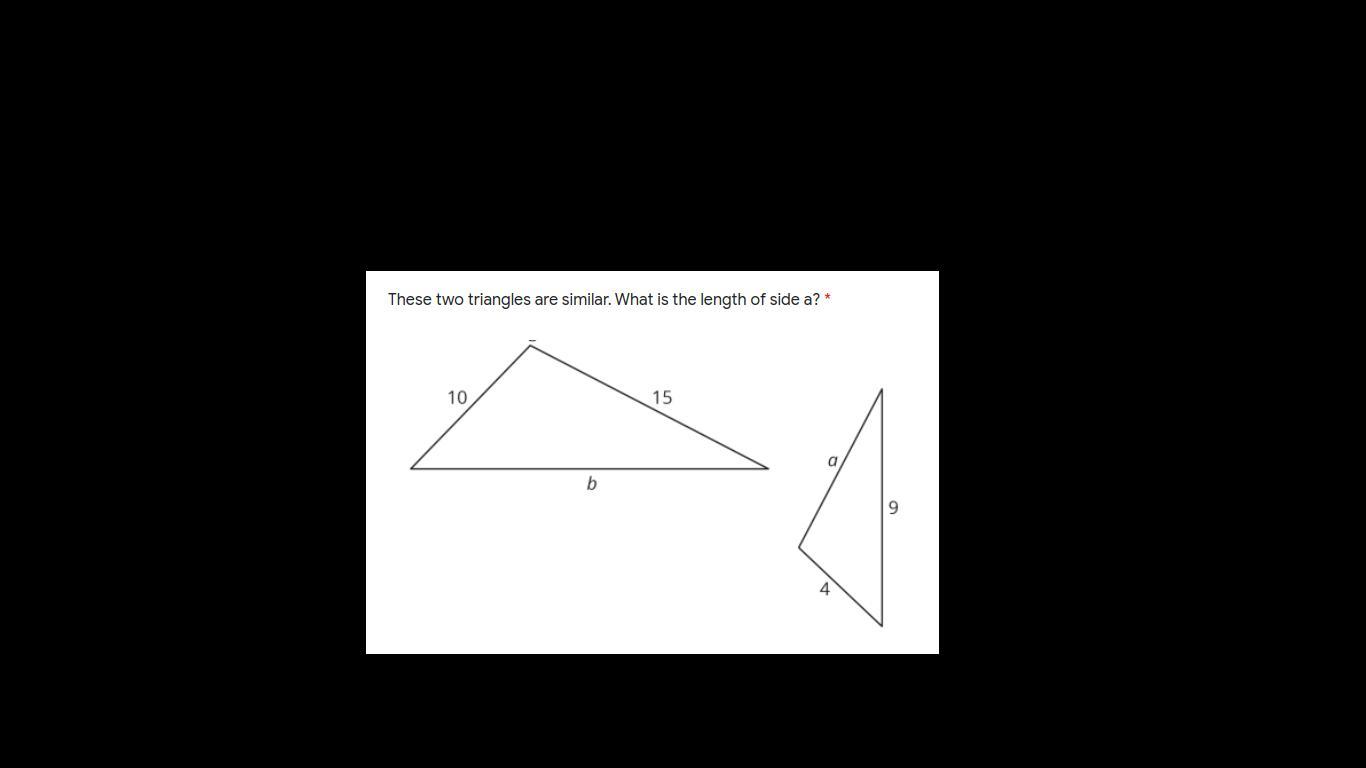
Answers
Answer:
do you have 12 as an answer?
Stefani took a science test. she answered 42 questions correctly. There were 50 questions on the test. What percent of the questions did she get right?
Answers
Answer:
She get 84% right
Step-by-step explanation:
42 x 2 = 84
50 x 2 = 100
Answer:
84%
this is the picture of how I solved it.
hope you understand.

In the figure, the radius of the large circle is three times the radius of the small circle. About what percent of the large circle is covered by the small circle?
I NEED THIS NOW PLEEEEEASE!!
Answers
The percent of the large circle is covered by the small circle will be 33.3%.
How to calculate the percentage?It should be noted that the radius of the small circle will be r.
The radius of the big circle will be 3r.
Therefore, the percent of the large circle is covered by the small circle will be:
= r / 3r × 100
= 1/3 × 100
= 33.3%
The percent of the large circle is covered by the small circle will be 33.3%.
Learn more about percentages on:
brainly.com/question/24877689
#SPJ1
an implicit equation for the plane passing through the point (−3,−4,−4) that is perpendicular to the line l(t)=⟨−5−4t,5 5t,4−2t⟩ is
Answers
To find the implicit equation for the plane passing through the point (-3,-4,-4) that is perpendicular to the line l(t) = <-5-4t, 5+5t, 4-2t>, we first need to find the normal vector of the plane.
Since the plane is perpendicular to the line, the normal vector of the plane will be parallel to the direction vector of the line. The direction vector of the line is < -4, 5, -2>, so the normal vector of the plane is also <-4, 5, -2>.
Next, we use the point-normal form of the equation of a plane:
(-4)(x+3) + (5)(y+4) - (2)(z+4) = 0
Expanding and simplifying:
-4x - 16 + 5y + 20 - 2z - 8 = 0
-4x + 5y - 2z - 4 = 0
Therefore, the implicit equation for the plane passing through the point (-3,-4,-4) that is perpendicular to the line l(t) = <-5-4t, 5+5t, 4-2t> is -4x + 5y - 2z - 4 = 0.
An implicit equation for the plane passing through the point (-3, -4, -4) and perpendicular to the line l(t) = ⟨-5 - 4t, 5 + 5t, 4 - 2t⟩ can be found by following these steps:
1. Find the direction vector of the line: To find the direction vector of the line l(t), look at the coefficients of the parameter t in the line equation: ⟨-4, 5, -2⟩.
2. Use the direction vector as the normal vector for the plane: Since the plane is perpendicular to the line, the normal vector of the plane will be the same as the direction vector of the line: ⟨-4, 5, -2⟩.
3. Use the normal vector and a point on the plane to find the equation of the plane: With the normal vector ⟨-4, 5, -2⟩ and the point (-3, -4, -4), plug the values into the general equation of a plane, Ax + By + Cz = D, where A, B, and C are the components of the normal vector:
-4(x - (-3)) + 5(y - (-4)) - 2(z - (-4)) = 0
Simplify the equation:
-4(x + 3) + 5(y + 4) - 2(z + 4) = 0
Your answer: -4(x + 3) + 5(y + 4) - 2(z + 4) = 0
Learn more about coefficients here: brainly.com/question/28975079
#SPJ11
Define a relation J on all integers: For all x, y e all positive integers, xJy if x is a factor of y (in other words, x divides y). a. Is 1 J 2? b. Is 2 J 1? c. Is 3 J 6? d. Is 17 J 51? e. Find another x and y in relation J.
Answers
Here is the summary of the relation J on all integers:
a. 1 J 2 : No
b. 2 J 1 : Yes
c. 3 J 6 : Yes
d. 17 J 51 : No
e. Another example of x and y in relation J: 4 J 12 (4 is related to 12 under relation J)
What is the relation J defined on all positive integers, and determine whether the integers are related under J?To define a relation J on all positive integers is following:
a. No, 1 is not a factor of 2, so 1 does not divide 2.
Therefore, 1 is not related to 2 under relation J.
b. Yes, 2 is a factor of 1 (specifically, 2 divides 1 zero times with a remainder of 1), so 2 divides 1.
Therefore, 2 is related to 1 under relation J.
c. Yes, 3 is a factor of 6 (specifically, 3 divides 6 two times with a remainder of 0), so 3 divides 6.
Therefore, 3 is related to 6 under relation J.
d. No, 17 is not a factor of 51, so 17 does not divide 51.
Therefore, 17 is not related to 51 under relation J.
e. Let's choose x = 4 and y = 12.
Then we need to check if x divides y. We can see that 4 is a factor of 12 (specifically, 4 divides 12 three times with a remainder of 0), so 4 divides 12.
Therefore, 4 is related to 12 under relation J.
To summarize:
1 is not related to 2 under relation J2 is related to 1 under relation J3 is related to 6 under relation J17 is not related to 51 under relation J4 is related to 12 under relation JLearn more about positive integers
brainly.com/question/26051073
#SPJ11
Mrs. Harrison made some muffins.
9 blueberry muffins
3 cranberry muffins
18 chocolate chip muffins
12 banana muffins
Which statement is correct?
A.
For every cranberry muffin, there are six banana muffins.
B.
For every blueberry muffin, there are four chocolate chip muffins.
C.
For every cranberry muffin, there are three banana muffins.
D.
For every blueberry muffin, there are two chocolate chip muffins.
Answers
Answer:D
Step-by-step explanation:
It’s D because 18 chocolate chip muffins and there are 9 blueberry muffins so for every blueberry muffin there is 2 chocolate chip muffins you could also do 18/9 and 2
Rewrite the equation shown in slope-intercept form. Identify the slope of the equation, the xintercept and the y-intercept. Then graph the equation. Make sure to show all your work in the
spaces provided.

Answers
Answer:
x^2 + 10
Step-by-step explanation:
Find the missing value.
Hint: Use the number line to find the missing value.
—9+
--
—3
主
-15
-10
-5
0
5
10
15

Answers
Answer:
-9 + 6 = -3
Step-by-step explanation:
The Number Line
The original number -9 is located as the red dot in the number line as shown in the figure below.
To move to the number -3 (as a blue dot) we must jump right 6 numbers. Thus, this is the number that must be filling the box.
-9 + 6 = -3

Which expressions are equivalent to One-half + 3 c + StartFraction 4 Over 5 EndFractionCheck all that apply. 3 c + StartFraction 4 Over 5 EndFraction + one-half 1 + 2 + 3c + 4 +5 StartFraction 4 Over 5 EndFraction + one-half + 3 c 2 + 3c + 4 One-half + StartFraction 4 Over 5 EndFraction + 3 c
Answers
Question:
Which expressions are equivalent to ½ + 3c + ⅘.
Check all that apply.
Answer:
½ + 3c + ⅘ is equivalent to
1. ⅒(30c + 13)
2. 3c + 13/10
Step-by-step explanation:
The options are not well presented.
However, I'll give simplify the given expression in the question above.
Given: ½ + 3c + ⅘.
Required: Simplify
We start by collecting like terms
3c + ½ + ⅘
From this point, the expression can be solved in two ways
1. Solve fractions
This gives [Find LCM]
3c + (5 + 8)/10
3c + 13/10
3c + ⅒(13)
This can still be solved further [Find LCM]
(30c + 13)/10
⅒(30c + 13)
Hence ⅒(30c + 13) is equivalent to ½ + 3c + ⅘.
2. Convert fractions to decimal
½ + 3c + ⅘ becomes
0.5 + 3c + 0.8
Collect like terms
3c + 0.5 + 0.8
3c + 1.3
Convert decimal to fraction
3c + 13/10
3c + ⅒(13)
This can still be solved further [Find LCM]
(30c + 13)/10
⅒(30c + 13)
Hence ⅒(30c + 13) is equivalent to ½ + 3c + ⅘.
This is as far as the expression can be evaluated
Answer:
1,3.and 5
Step-by-step explanation:
Which of the following sets of numbers could not represent the three sides of a righttriangle?{36, 76,85}Submit Answer{7, 24, 25){6,8,10}{21, 28, 35)
Answers
ANSWER:
\(\mleft\{36,76,85\mright\}\)STEP-BY-STEP EXPLANATION:
The right angles fulfill the Pythagorean theorem which is the following
\(h^2=a^2+b^2\)We evaluate each option, replacing:
\(\begin{gathered} 25^2=7^2+24^2\rightarrow625=625\text{ correct option} \\ 85^2=36^2+76^2\rightarrow7225=7072\text{ incorrect option} \\ 10^2=6^2+8^2\rightarrow100=100\text{ correct option} \\ 35^2=28^2+21^2\rightarrow1225=1225\text{ correct option} \end{gathered}\)In the diagram above <1=40%.find the measure of <2. <2=[?]%
![In the diagram above <1=40%.find the measure of <2. <2=[?]%](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/fYcRiQoLHbwPPJnnwQNofnNscBfNxyFL.jpeg)
Answers
Answer:
∠ 2 = 40°
Step-by-step explanation:
∠ 1 and ∠ 2 are corresponding angles and congruent, thus
∠ 2 = ∠ 1 = 40°
PLEASE ANSWER
What are the coordinates of the point that is one half the distance between A(−1, −2) and B(6, 12)?
( , )
Answers
Find the average of the x and y coordinates separately
help me :S POINTSSSSSSS

Answers
Answer: 10.5 ft^2
Step-by-step explanation:
\(A=\frac{a*b}{2} \\\\A=\frac{7*3}{2}\\\\A=10.5ft^{2}\)
Answer:
A) 21 ft
Step-by-step explanation:
So we are finding the area of a triangle so in that case we need to multiply.
L x W = Area
7 x 3 = 21
Find the inverse of the function f(x) = 2x - 4.
Answers
Answer:
f⁻¹(x) = 1/2 x + 2
Step-by-step explanation:
f(x) = 2x - 4 y=2x - 4
swap x and y: x = 2y - 4
solve y: 2y = x + 4
y = 1/2 x + 2
Inverse notation: f⁻¹(x) = 1/2 x + 2
Use the following notations: r = radius of a circle, v = linear velocity, w = angular velocity. Find the missing quantity. Round to the nearest tenth if necessary. V= 1235 m/min, r = 65 m, w = ?
Answers
The angular velocity of the circle is approximately 19 m/s.
In order to find the missing quantity, we can use the relationship between linear velocity and angular velocity in a circle. The linear velocity of a point on the edge of a circle is the product of the radius and the angular velocity. This can be expressed as:
v = r * w
where v is the linear velocity, r is the radius, and w is the angular velocity.
To find the value of w, we can rearrange this equation to solve for w:
w = v / r
Substituting the given values of v and r, we get:
w = 1235 m/min / 65 m
w = 19 m/s
It's important to note that units must be consistent when using formulas to solve problems. In this case, we converted the given linear velocity from m/min to m/s before plugging it into the formula. Also, we rounded the answer to the nearest tenth, as instructed, since the given values were rounded to the nearest unit.
To learn more about angular velocity
https://brainly.com/question/29557272
#SPJ4
the food marketing institute shows that of households spend more than per week on groceries. assume the population proportion is and a simple random sample of households will be selected from the population. use the z-table.
Answers
a) The sampling distribution of p can be approximated as a normal distribution with mean μp = .17 and standard deviation σp = .0203.
b) The probability that the sample proportion will be within ±.02 of the population proportion is 0.6778
In statistics, sampling distribution plays a crucial role in estimating the parameters of a population. The sampling distribution helps us to understand the probability distribution of sample statistics that we obtain by taking random samples from a population.
a) In this case, we are interested in the proportion of households that spend more than $100 per week on groceries, denoted by p. We know that the population proportion is p = .17, and a sample of 800 households will be selected from the population.
The central limit theorem states that if the sample size is large enough (in this case, n = 800), then the sampling distribution of p will be approximately normal with a mean of p and a standard deviation of:
σp = √(p(1-p)/n)
where p is the population proportion, and n is the sample size. Plugging in the values, we get:
σp = √(.17(1-.17)/800) = .0203
b) Now, we want to find the probability that the sample proportion will be within ±.02 of the population proportion. That is, we want to find P(.15 ≤ p ≤ .19).
To calculate this probability, we need to standardize the distribution using the z-score formula:
z = (p - μp) / σp
Plugging in the values, we get:
z = (.15 - .17) / .0203 = -0.9867
z = (.19 - .17) / .0203 = 0.9867
Using a standard normal distribution table or calculator, we can find the probabilities corresponding to these z-scores:
P(z ≤ -0.9867) = 0.1611
P(z ≤ 0.9867) = 0.8389
Therefore, the probability that the sample proportion will be within ±.02 of the population proportion is:
P(.15 ≤ p ≤ .19) = P(z ≤ 0.9867) - P(z ≤ -0.9867) = 0.8389 - 0.1611 = 0.6778
To know more about proportion here.
https://brainly.com/question/30657439
#SPJ4
Complete Question:
The Food Marketing Institute shows that 17% of households spend more than $100 per week on groceries. Assume the population proportion is p = .17 and a sample of 800 households will be selected from the population.
a. Show the sampling distribution of p, the sample proportion of households spending more than $100 per week on groceries.
b. What is the probability that the sample proportion will be within ±.02 of the population proportion?
A square piece of gold has sides that are 6 millimeters long. What is the piece of gold's area?
Answers
Step-by-step explanation:
It is a square so the sides are all equal
area = side X side
= 6 mm X 6 mm = 36 mm^2
Prove the function f :R- {1}\rightarrow?R-{1} defined by f(x)=(\frac{x+1}{x-1})^3is bijective.
Answers
The function f(x) = ((x+1)/(x-1))^3 is bijective as it is both injective and surjective, meaning it has a one-to-one correspondence between its domain and codomain.
To prove that f(x) = \(((x+1)/(x-1))^3\)is bijective, we need to show that it is both injective and surjective.
Injectivity: To prove injectivity, we assume that f(x1) = f(x2) and show that it implies x1 = x2. So, let's assume f(x1) = f(x2) and substitute the function values:
\(((x1+1)/(x1-1))^3 = ((x2+1)/(x2-1))^3\)
Taking the cube root of both sides, we get:
(x1+1)/(x1-1) = (x2+1)/(x2-1)
Cross-multiplying and simplifying, we have:
x1 + 1 = x2 + 1
This implies x1 = x2, which shows that the function is injective.
Surjectivity: To prove surjectivity, we need to show that for every y in the codomain, there exists an x in the domain such that f(x) = y. In this case, the codomain is R - {1}.
Let y be an arbitrary element in R - {1}. We can solve the equation f(x) = y for x:
\(((x+1)/(x-1))^3\)= y
Taking the cube root of both sides, we get:
\((x+1)/(x-1) = y^(1/3)\)
Cross-multiplying and simplifying, we have:
\(x + 1 = y^(1/3)(x - 1)\)
Expanding and rearranging terms, we get:
\((x - y^(1/3)x) = y^(1/3) - 1\)
Factoring out x, we have:
\(x(1 - y^(1/3)) = y^(1/3) - 1\)
Dividing both sides by (1 - y^(1/3)), we get:
\(x = (y^(1/3) - 1)/(1 - y^(1/3))\)
This shows that for any y in R - {1}, we can find an x in the domain such that f(x) = y, proving surjectivity.
Learn more about surjectivity here:
https://brainly.com/question/13656067
#SPJ11
Question is in image below.

Answers
Answer:
Step-by-step explanation:
Let's start with some conversions
-√113 = - 10.6301-120/11 = -10.90909-10.777... = -10.777...Remember that when you go to the negative side of the reals, the number that looks like it should be the largest, when negative is the smallest.
Answers
The smallest number of these three is -10.909
The second smallest is -10.777... repeat
The third smallest is -√113 which is -10.6301
The Largest one of the four is 10.7
Which decimal is equivalent to 19/4
Answers
Answer:
4.75
Step-by-step explanation:
19 divided by 4 is 4.75
Answer:
4.75
Step-by-step Explaination:
4×4=16
4×5=20
In 4 parts(.25, .50, .75, 20) 3rd is .75 so 4.75
Hope this will help you
if it is helpful please mark me as brainliest
Tanvi bought 48 rolls of paper towels. She got 1,116 meters of paper towels in all. How many
meters of paper towels were on each roll?
Write your answer as a decimal.
Answers
Answer: 23.25 meters on each roll
Step-by-step explanation:
simple division
6) Find the slope of AB.
A
(3,2)
B
(6,4)

Answers
Answer:
2 over 3
Step-by-step explanation:
whats her errors and whats the soulution

Answers
Answer:
she messed up at -17=34x
Step-by-step explanation:
she added 8x to each side but she was actually supposed to subtract
The error is 8(x - 3) + 7 = 2x(13) and -17 = 34x.
4 - 17 = -13, not 13
8x - 17 = 26x
-17 = 26x -8
-17 = 18x ( it should be like this, but this is still wrong because it should -26)
The solution is:
8(x - 3) + 7 = 2x(4 - 17)
8(x - 3) + 7 = 2x(-13)
8x - 24 + 7 = -26x
8x - 17 = -26x
8x + 26x = 17
34x = 17
x = 17/34
x = 1/2
Hope it helps!
Solve the equation for the given variable:
\( \frac{3(5y + 3)}{5} = 3y - 4\)
Answers
Answer:
Step-by-step explanation:
15y + 9 = 15y - 20
0 ≠ -29
no solution
Suppose that X has a discrete uniform distribution f(x)={ 1/4,
0,
x=1,2,3,4
otherwise
A random sample of n=36 is selected from this population. Find the probability that the sample mean is greater than 2.3 but less than 2.7, assuming that the sample mean would be measured to the nearest tenth.
Answers
The probability that the sample mean is greater than 2.3 but less than 2.7 is 0.0000000000000000000000000000000000019. This can be found by determining the probability that each individual observation falls within this range.
Given that X has a discrete uniform distribution, where each value has a probability of 1/4, we can calculate the probability of the sample mean falling within the specified range.
Since X follows a discrete uniform distribution with probabilities of 1/4 for each value (1, 2, 3, and 4), we need to find the probability that the sample mean falls between 2.3 and 2.7, considering measurement to the nearest tenth. To do this, we determine the probability of each individual observation falling within the range and then calculate the probability of the sample mean falling within the range.
In this case, the range can be rounded to the nearest tenth as (2.3, 2.4, 2.5, 2.6, 2.7). Since the values 2.4, 2.5, and 2.6 fall within the specified range, the probability of each of these individual observations occurring is 1/4.
To find the probability of the sample mean falling within the range, we need to account for the fact that it is the average of n observations. Since n = 36, the sample mean is the average of 36 observations. Therefore, the probability of the sample mean falling within the range of 2.3 to 2.7 is given by:
Probability = (Probability of each individual observation)^n
=\((1/4)^36\)
≈ 0.0000000000000000000000000000000000019 (rounded to decimal form)
Thus, the probability that the sample mean is greater than 2.3 but less than 2.7, assuming measurement to the nearest tenth, is approximately 0.0000000000000000000000000000000000019.
Learn more about probability here:
https://brainly.com/question/32117953
#SPJ11
let be a differentiable function where 9 and 4 and 3. if we change by -0.7 and we change by 0.3 then we can expect the value of to change by approximately what amount
Answers
If we change x by -0.7, we can expect the value of f(x) to decrease by approximately 2.1 units.
Assuming you meant to say "let f be a differentiable function where f(9) = 4 and f'(9) = 3. If we change x by -0.7 and we change y by 0.3, then we can expect the value of f(x) to change by approximately what amount?"
Using the linear approximation formula, we have:
\(Δf(x) ≈ f'(9) Δx\)
where Δx = -0.7 and we want to find Δf(x) when Δy = 0.3.
We can rearrange the formula to solve for Δf(x):
\(Δf(x) ≈ f'(9) Δx\)
Δf(x) ≈ 3(-0.7)
Δf(x) ≈ -2.1
This means that if we change x by -0.7, we can expect the value of f(x) to decrease by approximately 2.1 units. However, this is only an approximation based on the linear behavior of the function near x = 9, so it may not be exactly accurate for large changes in x.
Learn more about value here:
https://brainly.com/question/30145972
#SPJ11
dot mind the answer i clicked it was on accident but I need seriously help with this

Answers
No, The 3 house do not form of a right triangle because,
⇒ 1.2² + 1.9² < 2.4²
What is mean by Triangle?A triangle is a three sided polygon, which has three vertices and three angles which has the sum 180 degrees.
We know that;
Right triangle is satisfy the Pythagoras theorem.
If the sides of triangle are a, b and c.
Hence, We get;
⇒ a² + b² = c²
Here, The three distance are 1.2, 1.9 and 2.4.
Hence, We get;
⇒ 1.2² + 1.9²
⇒ 5.05
⇒ 2.4²
⇒ 5.76
Thus, We get;
⇒ 1.2² + 1.9² < 2.4²
Hence, The 3 house do not form of a right triangle because,
Learn more about the triangle visit;
brainly.com/question/1058720
#SPJ1
Prove the equation is true. State each trigonometric identity
used.
(1 + sin(−theta))(sec theta + tan theta) = cos(−theta)
Answers
To prove the equation (1 + sin(−θ))(sec θ + tan θ) = cos(−θ), the trigonometric indentities used are : sec θ = 1/cosθ, tanθ = sin θ/cosθ, sin(−θ)=sin(θ), cos(−θ)=cos(θ), cos² θ + sin² θ=1.
To prove the equation is true follow these steps:
Let's expand the left side using trigonometric identities: sec θ + tan θ = (1/cos θ) + (sin θ/cos θ)=(1 + sin θ)/cosθ. So, we get:(1 + sin(−θ))((1 + sin θ) / cos θ). Since sin(−θ)=sin(θ) ⇒ (1 - sin θ) (1 + sin θ) / cos θ ⇒ (1 - sin² θ) / cos θ [∵ a² - b² = (a+b)(a-b)]. Since,cos² θ + sin² θ=1 ⇒cos² θ / cos θ = cos(θ) [∵ 1 - sin² θ = cos² θ]. Hence, LHS= cos(θ)Let's expand the right side using trigonometric identities: Since cos(−θ)=cos(θ), RHS=cos(θ)Hence, the given equation is true. The trigonometric identities used in the proof are: sec θ = 1/cosθ, tanθ = sin θ/cosθ, sin(−θ)=sin(θ), cos(−θ)=cos(θ), cos² θ + sin² θ=1.
Learn more about trigonometric identities:
brainly.com/question/7331447
#SPJ11
An item sells for $75 and is on sale for 35% off. The sales tax is 9.8%. What is the final cost of the item?
Answers
The final cost of the item after a 35% discount and 9.8% sales tax is $53.54.
The given problem is related to percentage discounts and sales tax and can be solved using the following steps:
Step 1: Firstly, we need to determine the discount amount, which is 35% of the original price. Let's calculate it. Discount = 35% of the original price = 0.35 x $75 = $26.25
Step 2: Now, we will calculate the new price after the discount by subtracting the discount amount from the original price.New Price = Original Price - Discount AmountNew Price = $75 - $26.25 = $48.75
Step 3: Next, we need to calculate the amount of sales tax. Sales Tax = 9.8% of New Price Sales Tax = 0.098 x $48.75 = $4.79
Step 4: Finally, we will calculate the final cost of the item by adding the new price and the sales tax.
Final Cost = New Price + Sales Tax Final Cost = $48.75 + $4.79 = $53.54
Therefore, the final cost of the item after a 35% discount and 9.8% sales tax is $53.54.I hope this helps!
For more such questions on final cost
https://brainly.com/question/29509552
#SPJ8