Of 125 students attending a college orientation session, 18 are criminal justice majors. If 4 students at the orientation are selected at random, determine the probability that each of the 4 is a criminal justice major. Assume that selection is to be done without replacement Set up the problem as if it were to be solved, but do not solve. P(4 criminal justice majors selected) N
Answers
The probability that each of the 4 is a criminal justice major is equal to 0.0003 (rounded to four decimal places).
The probability of selecting 4 criminal justice majors from a group of 125 students, without replacement,
Using the hypergeometric probability distribution.
Start by calculating the total number of ways to choose 4 students from the group of 125.
C(125,4) = 125! / (4! (125-4)!)
= 125 x 124 x 123 x 122 / (4 x 3 x 2 x 1)
= 9,691,375
Next, calculate the number of ways to choose 4 criminal justice majors from the group of 18.
C(18,4) = 18! / (4! (18-4)!)
= 18 x 17 x 16 x 15 / (4 x 3 x 2 x 1)
= 3060
Finally,
Probability of selecting 4 criminal justice majors
= number of ways to choose 4 criminal justice majors / total number of ways to choose 4 students:
P(4 criminal justice majors selected) = C(18,4) / C(125,4)
⇒P(4 criminal justice majors selected) = 3060 / 9,691,375
= 0.0003157
Therefore, probability that each of the 4 students selected at random from the group of 125 students are criminal justice majors, without replacement is 0.0003 (rounded to four decimal places).
learn more about probability here
brainly.com/question/29047653
#SPJ4
Related Questions
Two angles are complementary. One angle is 5 times as large as the other angle. Find the measure of each angle.
Answers
Answer:
75 for the larger one, 15 for smaller
Step-by-step explanation:
Firstly, we have to know which angles are called Complementary Angles...
if we add two angles and the total will be equal to 90 deg
5:1
5*15=75
5*3=15
90
Find f ( - 3 ) for the function below.
{ ( - 3, 2 ), ( - 1, 0 ), ( 1, 1 ), ( 3, - 3 ) }
Answers
Answer:
Step-by-step explanation:
Question
Comment
The f(x) notation means that were ever you see n x on the right you put the value of x.
The question is which point has x = - 3 and what is the associated y value?
You could do it this way, just so you understand it.
X Y=========================
-3 2 <======
-1 0
1 1
3 -3
The answer must be the first one
Ned and Sarah were running a relay race .the race was 22.01 kilometers total if Ned ran 9.41 kilometers
Answers
Answer:
dwdwdadwdawddasd
Step-by-step explanation:
Mrs. Johnson bought 12 pound of ham and used it to make 3 sandwiches. She uses the same amount of ham on each sandwich. What fraction of a pound of ham is on each sandwich
Answers
The fraction of a pound of ham that each sandwich has for the case when Mrs Johson used 12 pounds of ham to make 3 sandwiches is 4 pound per ham. or 4/1
How to interpret the division?When 'a' is divided by 'b', then the result we get from the division is the part of 'a' that each one of 'b' items will get.
Thus, if 10 mangoes are there, and 2 people, then 10 ÷ 2 is the number of mangoes each person would get, which is 5.
Division, thus, can be interpreted as equally dividing the number that is being divided in total x parts, where x is the number of parts the given number is divided.
Thus, \(a \div b =\) a divided in b equal parts.
Also, we can write: \(a \div b = a \times \dfrac{1}{b}\)
(it is since a = a times 1 so \(a/b = 1 \times (a/b) = (1/b) \times a\))
For this case, we're specified that:
Total ham Mrs. Johnson bought = 12 poundsTotal sandwiches that she makes of that amount of ham = 312 pound of ham is divided in 3 parts for 3 sandwiches (assuming equally divided).
That means:
Amount of ham each sandwich gets = 12 divided by 3 = 12/3 = 4 pounds.
To find the fraction of a pound of ham that is on each sandwich, we find what part of a pound is 4 pounds.
If we take 4 times a pound, then we get 4 pounds.
Thus, 4 of a pound = 4 pound
In fraction, we have: 4 pounds = 4/1 fraction of a pound.
Thus, the fraction of a pound of ham that each sandwich has for the case when Mrs Johson used 12 pounds of ham to make 3 sandwiches is 4 pound per ham. or 4/1 fraction of a pound
Learn more about division here:
https://brainly.com/question/26411682
#SPJ1
Evaluate the expression 7x2−12x+13 when x=4. Show each step of your work by using the math keyboard under this question. First, show the value substituted in for x. Then show each step and rewrite the problem until it is complete
Answers
Answer:
-21
Step-by-step explanation:
7 x 2=14
14-48+13
14-48=-34
-34+13=-21
What shape is the cross section of a triangular pyramid sliced by a plane that is perpendicular to its base?
Answers
A triangle shape is formed by the cross-section of a triangular pyramid sliced by a plane that is perpendicular to its base
A triangular pyramid is a geometric solid having a triangle for a base and three triangles with the same vertex on each side. That is, the triangular pyramid is made up of four triangles. Pyramids made of triangles might be straight or inclined. It resembles a pyramid with four triangular faces that meet at one vertex and a triangular base.
Let's first draw the triangular pyramid. Now, mark the base. Then, denote the plane passing perpendicular to the base. From the diagram we can tell, the plane cuts this pyramid to form a triangle cross-section.
To know more about triangular pyramids:
https://brainly.com/question/22213308
#SPJ4

find the area of the kite below. A= blank
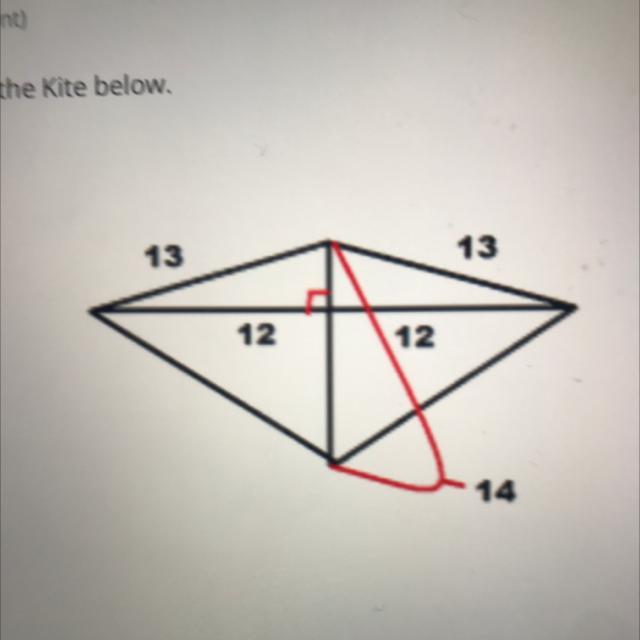
Answers
The area of the kite is 168 square units.
Area of kite
The general form of area of a kite is calculated by half the product of the lengths of its diagonals.
Then the formula to determine the area of a kite is:
Area = ½ × (d)1 × (d)2.
where (d)1 and (d)2 are long and short diagonals of a kite.
Given,
Here we have the diagram of the kite with side values.
Now, we have to find the area of the kite.
In order to find the area of the kite,
We have to identify the diagonals of the kite,
Here the values of the diagonals are 12 and 13.
Then the area of the kite is calculated as,
=> A = 1/2 x 24 x 14
=> A = 12 x 14
=> A = 168
Therefore the area of the kite is 168 square units.
To know more about Area of Kite here.
https://brainly.com/question/15640807
#SPJ1
A spinner with 4 equal sections is spun 20 times. The frequency of spinning each color is recorded in the table below.
Outcome Frequency
Pink 6
White 3
Blue 7
Orange 4
What statement best compares the theoretical and experimental probability of landing on blue?
The theoretical probability of landing on blue is one fourth, and the experimental probability is 35%.
The theoretical probability of landing on blue is one fourth, and the experimental probability is 50%.
The theoretical probability of landing on blue is one fifth, and the experimental probability is 35%.
The theoretical probability of landing on blue is one fifth, and the experimental probability is 50%.
Answers
Answer:
Step-by-step explanation:
The statement that best compares the theoretical and experimental probability of landing on blue is:
The theoretical probability of landing on blue is one fourth, and the experimental probability is 35%.
Theoretical probability is the probability of an event occurring based on the assumption that the spinner is fair, and the experimental probability is the probability of an event occurring based on the data collected from the spins.
Since the spinner has four equal sections, the theoretical probability of landing on any section is 1/4 or 25%. Therefore, the theoretical probability of landing on blue is 1/4 or 25%.
On the other hand, the experimental probability is the number of times an event occurs, divided by the total number of trials.
In this case, the experimental probability of landing on blue is 7/20 or 35%.
So the theoretical probability of landing on blue is one fourth or 25% and the experimental probability is 35%.
suppose that c→=a→−b→. under what circumstances is the length of c→ equal to the sum of the lengths a→ and b→ ?
Answers
The length of c→ is equal to the sum of the lengths of a→ and b→ when c→ is a perpendicular vector to both a→ and b→, meaning that c→ is at a right angle to both a→ and b→.
This is due to the fact that the length of a vector is equal to the length of the hypotenuse of a right triangle, which is the sum of the lengths of the other two sides (a→ and b→). When c→ is perpendicular to both a→ and b→, the right triangle formed by a→, b→, and c→ is a special type of right triangle called a Pythagorean triangle, in which the length of the hypotenuse (c→) is equal to the sum of the lengths of the other two sides (a→ and b→). Thus, the length of c→ is equal to the sum of the lengths of a→ and b→ when c→ is perpendicular to both a→ and b→.
know more about Pythagorean triangle here
https://brainly.com/question/13095504#
#SPJ11
find dy/dx by implicit differentiation. y sin(x2) = x sin(y2)
Answers
The derivative dy/dx of the equation ysin(x^2) = xsin(y^2) is given by (sin(y^2) - ycos(x^2)2x) / (sin(x^2) - 2yxcos(y^2)).
In the given equation, y and x are both variables, and y is implicitly defined as a function of x. To find dy/dx, we differentiate each term using the chain rule and product rule as necessary.
Differentiating the left-hand side of the equation, we apply the product rule to ysin(x^2). The derivative of ysin(x^2) with respect to x is dy/dxsin(x^2) + ycos(x^2)*2x.
Differentiating the right-hand side of the equation, we apply the product rule to xsin(y^2). The derivative of xsin(y^2) with respect to x is sin(y^2) + x*cos(y^2)2ydy/dx.
Now we have two expression for the derivative of the left and right sides of the equation. To isolate dy/dx, we can rearrange the terms and solve for it.
Taking the derivative of ysin(x^2) = xsin(y^2) with respect to x using implicit differentiation yields:
dy/dxsin(x^2) + ycos(x^2)2x = sin(y^2) + xcos(y^2)2ydy/dx.
By rearranging the terms, we can solve for dy/dx:
dy/dx * (sin(x^2) - 2yxcos(y^2)) = sin(y^2) - y*cos(x^2)*2x.
Finally, we can obtain the value of dy/dx by dividing both sides by (sin(x^2) - 2yxcos(y^2)):
dy/dx = (sin(y^2) - ycos(x^2)2x) / (sin(x^2) - 2yxcos(y^2)).
Learn more about implicit differentiation here brainly.com/question/31568657
#SPJ11
Use the following tables to compose q(r(5))

Answers
Answer:
d. 289
Explanation:
You want to solve the function of q when function of r has an input of 5.
Might sound confusing but find the output of function r(x) with the input of
x = 5.
From the r(x) chart:
r(5) = -17
Now substitute that in the original question:
q(r(5)) = q(-17)
Look at the q(x) chart next, as you can see:
q(-17) = 289
So all in all:
q(r(5)) = 289
Cheers!
HELP ME PLEASE!!!!!!

Answers
Answer:
53 people
Step-by-step explanation:
\(\frac{2}{5}\) × 120 = = 48
48 + 5 = 53 people
____
You've made your grade level high school, lower it to Grade 4. Thank you!
Use cofunctions of complementary angles to complete the relationship. cos (pi/3)=sin() Find the lengths of the missing sides if side a is opposite angle A, side b cos(B) = 4/5, a = 50
Answers
The relationship between cosine and sine of complementary angles allows us to complete the given equation. Using the cofunction identity, we know that the cosine of an angle is equal to the sine of its complementary angle.
If cos(pi/3) = sin(), we can determine the value of the complementary angle to pi/3 by finding the sine of that angle. To find the lengths of the missing sides in a right triangle, we can use the given information about the angle B and side a. Since cos(B) = 4/5, we know that the adjacent side (side b) is 4 units long and the hypotenuse is 5 units long. Using the Pythagorean theorem, we can find the length of the remaining side, which is the opposite side (side a). Given that a = 50, we can solve for the missing side length. In summary, using the cofunction identity, we can determine the value of the complementary angle to pi/3 by finding the sine of that angle. Additionally, using the given information about angle B and side a, we can find the missing side length by using the Pythagorean theorem.
Learn more about Pythagorean theorem here:
https://brainly.com/question/14930619
#SPJ11
a rectangular field is twice as long as it is wide. if 3 feet are taken from the width, and 4 feet taken from the length, the resultant are of the field is 180 2 ft . find the area of the original field.
Answers
The original area of the given rectangular field be 288 ft²
Given, a rectangular field is twice as long as it is wide.
Now, if 3 feet are taken from the width and 4 feet are taken from the length then the resultant area of the field of the field be 180 ft².
We have to find the original area of the field.
Let the original length of the rectangular field be, l
and original breadth of the rectangular field be, b
Now, l = 2b
New length be, (2b - 4)
New breadth be, (b - 3)
New area be, 180
(2b - 4)(b - 3) = 180
2b² - 10b + 12 = 180
b² - 5b + 6 = 90
b² - 5b - 84 = 0
b² - 12b + 7b - 84 = 0
b(b - 12) + 7(b - 12) = 0
(b - 12)(b + 7) = 0
As, breadth can not be negative, therefore the breadth be 12 ft.
and length be 24 ft.
Original area be,
Area = 12×24
Area = 288 ft²
Hence, the original area be 288 ft²
Learn more about Areas and Perimeter here https://brainly.com/question/27430555
#SPJ4
The following cone has a slant height of 17
cm and a radius of 8
cm.
What is the volume of the cone?
Responses
480π
320π
544π
Answers
The formula for the volume of a cone is:
V = (1/3)πr²h
where r is the radius of the base, h is the height of the cone, and π is pi.
In this case, the slant height is given as 17 cm, which we can use with the radius to find the height of the cone using the Pythagorean theorem:
h² = s² - r²
h² = 17² - 8²
h² = 225
h = 15
Now that we have the height, we can plug in the values for r and h into the formula for the volume:
V = (1/3)π(8²)(15)
V = (1/3)π(64)(15)
V = (1/3)(960π)
V = 320π
Therefore, the volume of the cone is 320π cubic cm. Answer: 320π.
What is the slope of the line that passes through the points (-9,8) and (-21,10)?

Answers
Answer:
-1/6
Step-by-step explanation:
https://brainly.com/question/20487549
The slope is -1/6
Step-by-step explanation:
We simply use the slope formula here
Mathematically, we have this as;
m = (y2-y1)/(x2-x1)
thus;
m = (10-8)/(-21 + 9) = 2/-12 = -1/6
The slope of a line that passes through the points (-9,8) and (-21,10) is -1/6
What is slope?The slope of a linear graph is the rate of change of the graph
From the question, we have the following ordered pairs
(x,y) = (-9,8) and (-21,10)
So, the rate of change (m) is then calculated as:
\(m =\frac{y_2 -y_1}{x_2 -x_1}\)
This gives
\(m =\frac{10 - 8}{-21 + 9}\)
Evaluate the differences
\(m =\frac{2}{-12}\)
Evaluate the quotient
\(m =-\frac{1}{6}\)
Hence, the slope is -1/6
Read more about rate of change at:
https://brainly.com/question/1884491
Two teams are playing in the finals for an adult softball league. Each team has 13 players and the ages of the team members are shown in the tables. Which statement is true?
A) The mean for team 1 is greater than the mean for team 2.
B) The median for team 1 is greater than the median for team 2.
C) The median for team 2 is greater than the median for team 1.
D) The value of Q1 for team 1 is greater than the value of Q1 for team 2.
Answers
Answer:
B
Step-by-step explanation:
The formula to compute a person's body mass index is B= 703x w/h2. B represents the body mass index, is the person's weight in pounds and represents the person's height in inches.
a. Solve the formula for w.
b. Find the weight to the nearest pound of a person who is 64 inches tall and has a body mass index of 21.45.
Answers
a. The formula B = 703w/h^2 can be solved for w by rearranging the equation as w = B * h^2 / 703.
b. For a person who is 64 inches tall and has a body mass index of 21.45, the weight can be calculated by substituting the values into the formula w = B * h^2 / 703, where B is 21.45 and h is 64 inches.
a. To solve the formula B = 703w/h^2 for w, we can rearrange the equation to isolate w on one side of the equation. Multiply both sides of the equation by h^2, then divide both sides by 703. The resulting equation is w = B * h^2 / 703.
b. To find the weight of a person who is 64 inches tall and has a body mass index of 21.45, we can substitute the values into the formula w = B * h^2 / 703. In this case, B is 21.45 and h is 64 inches. Plugging these values into the equation, we get w = 21.45 * 64^2 / 703. Evaluating this expression will give us the weight in pounds.
Learn more about equation here
https://brainly.com/question/29657983
#SPJ11
Find an equation of the sphere that passes through the point (4 3 -1) and has center (3 8 1)
Answers
The equation of the sphere that passes through the point (4, 3, -1) and has a center at (3, 8, 1) is: (x - 3)^2 + (y - 8)^2 + (z - 1)^2 = 30.
To find the equation of the sphere passing through the point (4, 3, -1) with a center at (3, 8, 1), we can use the general equation of a sphere:
(x - h)^2 + (y - k)^2 + (z - l)^2 = r^2
where (h, k, l) represents the center of the sphere and r represents the radius.
First, we need to find the radius. The distance between the center and the given point can be calculated using the distance formula:
√[(x2 - x1)^2 + (y2 - y1)^2 + (z2 - z1)^2]
Substituting the coordinates of the center (3, 8, 1) and the given point (4, 3, -1), we have:
√[(4 - 3)^2 + (3 - 8)^2 + (-1 - 1)^2]
Simplifying, we get:
√[1 + 25 + 4] = √30
Therefore, the radius of the sphere is √30.
Now we can substitute the center (3, 8, 1) and the radius √30 into the general equation:
(x - 3)^2 + (y - 8)^2 + (z - 1)^2 = 30
So, the equation of the sphere that passes through the point (4, 3, -1) and has a center at (3, 8, 1) is:
(x - 3)^2 + (y - 8)^2 + (z - 1)^2 = 30.
This equation represents all the points on the sphere's surface.
Know more about sphere here,
https://brainly.com/question/22849345
#SPJ11
The three angle bisectors of a triangle are concurrent. Their point of concurrence is called the ____.
Answers
The three angle bisectors of a triangle are concurrent. Their point of concurrence is called the incenter.
The triangle's three angle bisectors are contemporaneous, which means they cross at the same place.
The incenter is the location where the angle bisectors coincide.
1. The circle's inscribed center is known as the incenter.
2. The incenter is equidistant from the triangle's sides.
More examples of agreement
The centroid is the location where all of a triangle's medians meet.
The triangle's circumcenter is where the perpendicular bisectors of its sides meet.
The intersection of the perpendiculars emanating from the vertices on the opposing sides of a triangle is known as the orthocentre.
Know more about incenter
https://brainly.com/question/1831482
#SPJ4
A yearbook has 32 pages, and each page has 8 pictures on it. Estimate how manypictures are in the yearbook.
Answers
To find how many picture are in the yearbook, multiply the number of pages of the yearbook by the number of pictures on one page. This is 32 times 8:
\(32\cdot8=256\)There are 256 picture in the yearbook.
what is the equation?
Answers
Answer:what equation ?
Step-by-step explanation:
Answer:
to what ..............
an asteroid travels at the speed of 7^8 miles per day. how many miles will it travel in 7^3 days
Answers
The asteroid will travel \(7^{11}\) miles in \(7^3\) days. Speed is a measure of how fast an object moves, typically given in units like meters per second or miles per hour.
Distance, on the other hand, refers to the total amount of ground covered by an object during its movement from one point to another.
To find out how many miles the asteroid will travel in \(7^3\) days, we can use the formula: distance = speed × time.
The given speed of the asteroid is \(7^8\) miles per day.
To find the distance traveled in \(7^3\) days, we need to multiply the speed by the time.
So, the distance traveled = (\(7^8\) miles per day) × (\(7^3\) days).
To multiply powers with the same base, we add their exponents. Therefore, \(7^8\) × \(7^3\) = \(7^{(8+3)}\) = \(7^{11}\).
Hence, the asteroid will travel \(7^{11}\) miles in \(7^3\) days.
To know more about Distance visit:
https://brainly.com/question/28762900
#SPJ11
2. 4Cl₂ + 1002 →
a. 2Cl₂05
b. 4C1₂05
c. 14C1₂05
d. 40C1₂05
This is a type of chemical of physical
reaction, please make sure you draw it so I can have a reference if you mind thank you.
Answers
The balanced chemical equation for the reaction is: 8Cl₂ + 10O2 → 4Cl₂O5.
What is equation?An equation is a mathematical statement that shows the equality of two expressions, usually with an equal sign "=" in between them. An equation can contain variables, constants, and operators. The variables are represented by letters and can take on different values, while constants are fixed values that do not change. Operators include mathematical symbols like plus, minus, multiplication, and division, as well as exponents and logarithms.
Here,
This is a synthesis or combination reaction, where two or more reactants combine to form a single product. In this case, chlorine gas (Cl₂) and oxygen gas (O2) combine to form chlorine oxide (Cl₂O5).
To know more about equation,
https://brainly.com/question/2228446
#SPJ1
9.36 divided by 0.52
Answers
Answer:
9.36 / 0.52 = 18
Step-by-step explanation:
Divide them.
If Sale price = Rs 450 Discount amount = 50 Find the Discount % *
Answers
Answer:
The discount percentage is 11.1%
Step-by-step explanation:
Here, we want to find the percentage of discount
We simply place the discount amount over the sales price multiplied by 100
we have this as;
50/450 * 100%
= 1/9 * 100%
= 100%/9
= 11.1%
Consider these three numbers expressed in scientific notation: 8.2 × 10-3, 5.2 × 10-6, and 4.1 × 10-6. which number is the greatest, and by how many times is it greater than the smallest number? a. the greatest number is 8.2 × 10-3. it is 20 times greater than the smallest number. b. the greatest number is 5.2 × 10-6. it is 20 times greater than the smallest number. c. the greatest number is 8.2 × 10-3. it is 2,000 times greater than the smallest number. d. the greatest number is 5.2 × 10-6. it is 2,000 times greater than the smallest number.
Answers
C)The greatest number is 8.2 × 10-3. It is 2,000 times greater than the smallest number.
In scientific notation, a number is written as the product of a number between 1 and 10 and a power of 10. The power of 10 tells us how many places to move the decimal point to the right (if the exponent is positive) or to the left (if the exponent is negative).
In this case, 8.2 × 10-3 means 8.2 × (10^-3) = 0.0082, 5.2 × 10-6 means 5.2 × (10^-6) = 0.0000052 and 4.1 × 10-6 means 4.1 × (10^-6) = 0.0000041.
To compare the numbers, we can compare the coefficient or the number in front of the 10 power. We can see that 8.2 is greater than 5.2 and 4.1. To check how many times greater the smallest number is, we can use the following formula: (greatest number / smallest number) = (8.2 / 0.0000041) = 2,000
Therefore, the greatest number is 8.2 × 10-3 and it is 2,000 times greater than the smallest number.
For more questions like Scientific notation click the link below:
https://brainly.com/question/21289208
#SPJ4
]
an experiment is performed and four events (a, b, c, and d) are defined over the set of all possible outcomes. the probabilities of the four events and their intersections are:which pair of states are independent?
Answers
To determine which pair of events are independent, we need to check if the probability of their intersection is equal to the product of their individual probabilities. If the two probabilities are equal, the events are independent; otherwise, they are dependent.
Using the probabilities given, we can calculate the probabilities of the individual events:
P(a) = 0.4
P(b) = 0.3
P(c) = 0.2
P(d) = 0.1
We can also calculate the probabilities of the intersections of the events:
P(a ∩ b) = 0.1
P(a ∩ c) = 0.1
P(a ∩ d) = 0.1
P(b ∩ c) = 0.05
P(b ∩ d) = 0.05
P(c ∩ d) = 0.01
Now, we can check the pairs of events for independence:
1. Events a and b:
P(a) * P(b) = 0.4 * 0.3 = 0.12
P(a ∩ b) = 0.1
Since P(a ∩ b) is not equal to P(a) * P(b), events a and b are dependent.
2. Events a and c:
P(a) * P(c) = 0.4 * 0.2 = 0.08
P(a ∩ c) = 0.1
Since P(a ∩ c) is greater than P(a) * P(c), events a and c are dependent.
To learn more about Ka, refer below:
brainly.com/question/28649738
#SPJ11
3. Events a and d:
P(a) * P(d) = 0.4 * 0.1 = 0.04
P(a ∩ d) = 0.1
Since P(a ∩ d) is greater than P(a) * P(d), events a and d are dependent.
4. Events b and c:
P(b) * P(c) = 0.3 * 0.2 = 0.06
P(b ∩ c) = 0.05
Since P(b ∩ c) is not equal to P(b) * P(c), events b and c are dependent.
5. Events b and d:
P(b) * P(d) = 0.3 * 0.1 = 0.03
P(b ∩ d) = 0.05
Since P(b ∩ d) is not equal to P(b) * P(d), events b and d are dependent.
6. Events c and d:
P(c) * P(d) = 0.2 * 0.1 = 0.02
P(c ∩ d) = 0.01
Since P(c ∩ d) is not equal to P(c) * P(d), events c and d are dependent.
Therefore, none of the pairs of events are independent.
To learn more about probability refer below:
https://brainly.com/question/32004014
#SPJ11
Which polynomial function has a leading coefficient of 3 and roots –4, i, and 2, all with multiplicity 1? f(x) = 3(x 4)(x – i)(x – 2) f(x) = (x – 3)(x 4)(x – i)(x – 2) f(x) = (x – 3)(x 4)(x – i)(x i)(x – 2) f(x) = 3(x 4)(x – i)(x i)(x – 2)
Answers
The polynomial function with leading coefficient of 3 and root -4, i, and 2 all with multiplicity of 1 is f(x) = 3(x+4)(x-i)(x+2)
Polynomial function
The Leading coefficients are the numbers written in front of the variable with the largest exponent.
Roots of a polynomial refer to the values of a variable for which the given polynomial is equal to zero.
The multiplicity is the number of times a given factor appears in the factored form of the equation of a polynomial.
Therefore, the polynomial f(x) = 3(x+4)(x-i)(x+2) has a root -4 , 1 and -2.
The leading coefficient is 3. The multiplicity is all one.
learn more on polynomial here: https://brainly.com/question/13309002
#SPJ4
Answer:
d
Step-by-step explanation:
What are the exact solutions of x2 − 3x − 1 = 0 using x equals negative b plus or minus the square root of the quantity b squared minus 4 times a times c all over 2 times a?
Answers
Answer:
The solution of the equation is 3.3 and (-0.3).
Step-by-step explanation:
We need to find the exact solution of the given quadratic equation \(x^2-3x-1=0\).
If the quadratic equation is in the form of \(ax^2+bx+c=0\), then the solution of this equation is given by :
\(x=\dfrac{-b\pm \sqrt{b^2-4ac} }{2a}\)
On comparing the given equation with this above, it means, a = 1, b = -3 and c = -1.
So,
\(x=\dfrac{-(-3)\pm \sqrt{(-3)^2-4\times 1\times (-1)} }{2\times 1}\\\\x=\dfrac{-(-3)+\sqrt{(-3)^{2}-4\times1\times(-1)}}{2\times1}, \dfrac{-(-3)-\sqrt{(-3)^{2}-4\times1\times(-1)}}{2\times1}\\\\x=3.3, -0.30\)
So, the solution of the equation is 3.3 and (-0.3).
Answer:
1
-3
-1
Step-by-step
got it 100% correct