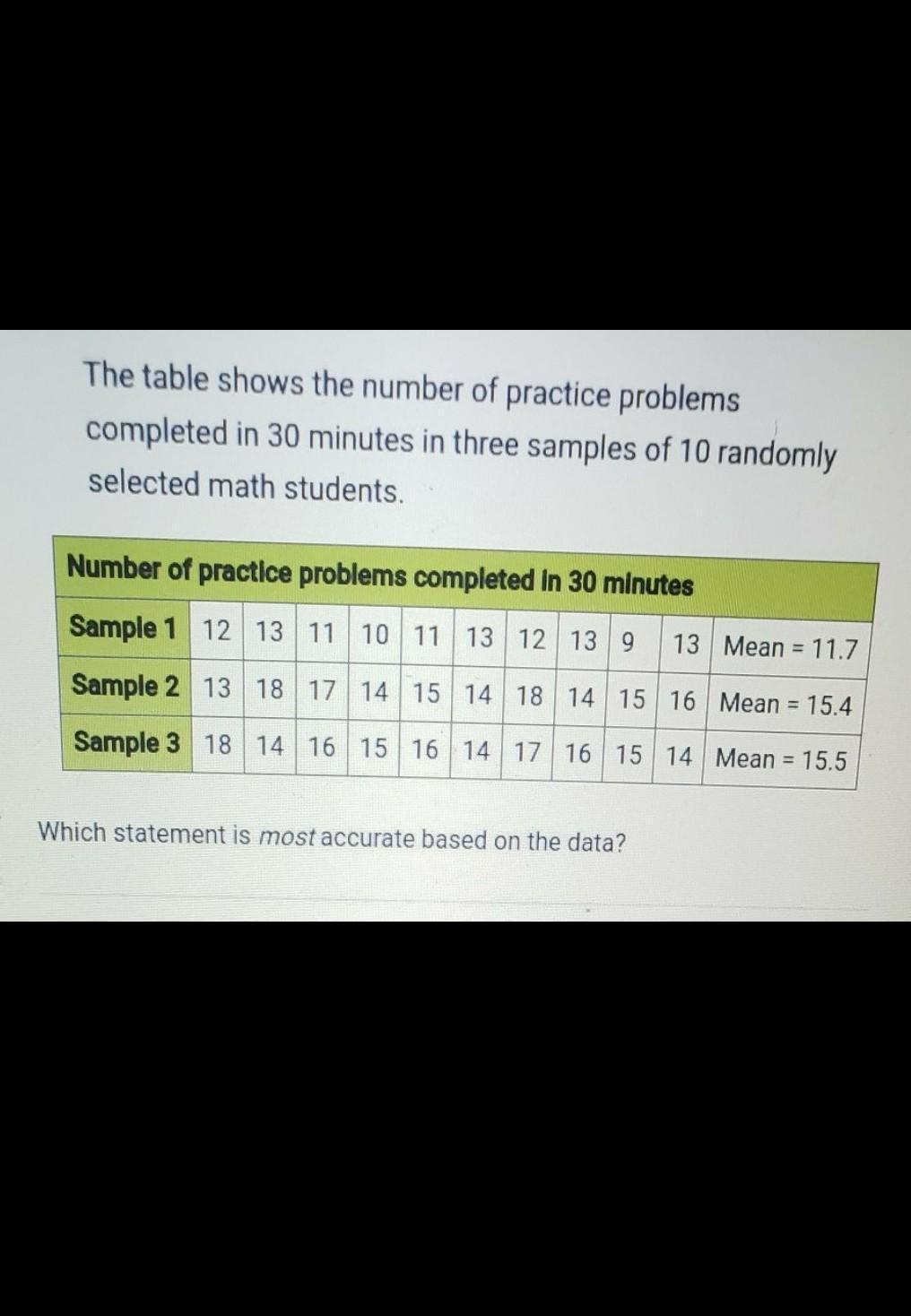
O A. A prediction based on the data is reliable, because there are nonoticeable differences among the samples.OB. A prediction based on the data is not completely reliable, becausethe mean of sample 1 is noticeably lower than the means of theother two samples.C. A prediction based on the data is not completely reliable, becausethe means of samples 2 and 3 are too close together.OD. A prediction based on the data is reliable, because the means ofsamples 2 and 3 are very close together.
Answers
The mean is a reliable measure of the central tendency when the data are normally distributed but when the data are skewed, the mean is less relaible.
In our case, we can see that there are not many outliers because the means are very close, then, the answer is
A) A prediction based on the data is reliable, because there are no noticeable differences among the samples.
Related Questions
The variables y and x have a proportional relationship, and y = 12 when x = 5.
What is the value of y when x = 8?
Answers
Y= 19.2
Answer:
y = 19.2
Step-by-step explanation:
We know there is relationship between y and x, so according to the formula \(y = kx\)
k = 12/5
we get one function y = 2.4x
when x = 8, input it into the function,
y = 2.4×8 = 19.2
The formulas for total revenue and total cost, in hundreds of dollars, for selling and producing q hundred Items are: total revenue: TR(q) = 30q total cost: Tc(q) = q^3-15q^2+75q+10. (a) Find the smallest quantity at which marginal cost is equal to 15 dollars per Item. (b) Recall: Fixed cost is given by FC = TC(0). Variable cost is given by VC(q) = TC(q) - FC. Average variable cost is given by AVC(q) = VC(q)/q. Find a positive value of q at which average variable cost is equal to marginal cost. (c) Find the longest interval on which marginal revenue exceeds marginal cost. (d) Recall that profit is given by P(q) = TR(q)-TC(q) and On an interval of quantities where MR(q) < MC(q), profit is decreasing. On an interval of quantities where MR(q) > MC(q), profit is increasing Use the sketch you drew in part (c) to find the quantity at which profit is greatest. What is the maximum value of profit?
Answers
(a). The smallest quantity at which marginal cost is equal to 15 dollars per item is 2.76. (b). The positive value of q at which average variable cost is equal to marginal cost is \(\frac{15}{2}\). (c). The longest interval on which marginal revenue exceeds marginal cost is (1.8377, 8.1622). (d). The profit is increasing at 8.1622 at p(q) is maximum. (e). The maximum value of profit is 78.2455 dollars.
The total revenue: TR(q) = 30q
The total cost: Tc(q) = \(q^3-15 q^2+75 q+10$\)
The change in cost is referred to as the change in the cost of production when there is a need for change in the volume of production.
(a). Marginal cost MC\(=\frac{\partial}{\partial q}(T C)$\)
\($$=3q^2-30 q+75 \text {. }$$\)
According to question.
\($$\begin{aligned}& 3 q^2-30 q+75=15 \\& 3 q^2-30 q+60=0 \\& q^2-10 q+20=0 \\& q= \frac{10 \pm \sqrt{100-80}}{2} \\&= \frac{10 \pm 2 \sqrt{5}}{2}=5 \pm \sqrt{5}\end{aligned}\)
\($$$\therefore \quad q=5+\sqrt{5} \quad$ and $q=5-\sqrt{5}$\)
we have to find smallest quantity.
\($$\therefore \quad q=5-\sqrt{5}=2.76 \text {. }$$\)
b)
\($$\begin{aligned}& F C=T C(0)=10 \\& V C(q)=T C(q)-F C \\& =q^3-15 q^2+75 q . \\& \text { AVC(q) }=\frac{V C(q)}{q}=q^2-15 q+75 .\end{aligned}$$\)
When AVC(q)=MC(q)
\($$\begin{array}{ll}\Rightarrow & q^2-15 q+7 ;=3 q^2-30 q+75 \\\Rightarrow & 2 q^2-15 q=0 .\ \Rightarrow q(2 q-15)=0 . \\\Rightarrow & q=0, \frac{15}{2} \quad \Rightarrow \quad q=\frac{15}{2}\end{array}$$\)
Therefore, the positive value of q at which average variable cost is equal to marginal cost is \(\frac{15}{2}\).
(c).
\(& M R(q)=\frac{d}{d q}(T R)=30 . \\\)
\(& M C(q)=3 q^2-30 q+75 . \\\)
Let MR(a)>MC(q)
\(& \Rightarrow \quad 30 > 3 q^2-30 q+75 \text {. } \\\)
\(& \Rightarrow \quad 3 q^2-3 p q+45 < 0 \\\)
\(& \Rightarrow \quad q^2-10 q+15 < 0 \text {. } \\\)
\(& \because \quad q=\frac{10 \pm \sqrt{100-60}}{2} \Rightarrow q=\frac{10 \pm 2 \sqrt{10}}{2} \\\)
\(& q=(5 \pm \sqrt{10}) \\\)
\(& \Rightarrow \quad(q-5+\sqrt{10})(q-5-\sqrt{10}) < 0 . \\\)
\(& \Rightarrow \(q-5+\sqrt{10}) < 0 \quad \& \quad(q-5-\sqrt{10}) > 0 \text {. } \\\)
\(& \text { or } \quad(q-5+\sqrt{10}) > 0 \quad \& \quad(q-5-\sqrt{10}) < 0 \text {. } \\\)
\(& \therefore \quad \text { other } q < 5-\sqrt{10}=1.8377 ., q > 5+\sqrt{10}=8.1622 \text {. } \\\)
\(& \Rightarrow \quad q < 1.8377 \& q > 0.1622 \text {. } \\\)
\(& \text { or } q > 5-\sqrt{10} \quad \& \quad q < 5+\sqrt{10} \text {. } \\\)
\(& \Rightarrow q > 1.8377 \quad < q < 8.1622 \text {. } \\\)
The Interval is (1.8377, 8.1622).
(d). P(q) =TR(q)-TC(q)
\(& =30 q-\left(q^3-15 q^2+75 q+10\right) \\& =-q^3+15 q^2-75 q-10+30 q \\& =-q^3+15 q^2-45 q-10 .\)
on (1.8377,8.1622). we have to find a point such that p"(q)=0 and p"(q)<0.
\(& p^{\prime}(q)=-3 q^2+30 q-45 \\\)
\(& \Rightarrow \quad-3\left(q^2-10 q+15\right)=0 \\\)
\(& \Rightarrow \quad q^2-10 q+15=0 . \\\)
\(& \quad q=1.8377 \text { and } \quad q=8.1622 . \\\)
\(& \Rightarrow \quad p^{\prime \prime}(q)=-6 q+30 . \\\)
\(& p^{\prime \prime}(1.8377)=-6(1.8377)+30 \\\)
\(&=18.9738 \\\)
\(& p^{\prime \prime}(8.1622)=-6(8.1622)+30 . &=-18.9732 < 0 .\)
at 8.1622, p(q) is maximum.
(e).
Max profit-P(8.1622)
=78.2455 dollars
Therefore, the maximum value of profit is 78.2455 dollars.
For more such questions on Marginal cost
https://brainly.com/question/16027422
#SPJ4

{ (-2, 4), (0, 2), (-1, 3), (4, -2)}
The set of ordered pairs above:
DONE
Domain
-3
4
-1
5
Range
3
7
-2
The mapping diagram above:
DONE
y=x²
DONE
x
-3
-1
y
5
2
-1
The table above:
DONE ✔

Answers
The set of ordered pairs above: is a function.
The mapping diagram above: is a function.
y = x²: is a function.
The table above: is not a function.
What is a function?In Mathematics and Geometry, a function is a mathematical equation which is typically used for defining and representing the relationship that exists between two or more variables such as an ordered pair.
Based on the set of ordered pairs, mapping diagram, and the equation above, we can reasonably infer and logically deduce that it represent a function because the input values (domain, x-value, or independent values) are uniquely mapped to the output values (range, y-value or dependent values).
In this context, we can reasonably infer and logically deduce that the table does not represent a function because the input value (-1) has more than output values (2 and 4 respectively).
Read more on function here: brainly.com/question/27862183
#SPJ1
Find the zeros of the function and state the multiplicities.
k(x)=15x³-48x²-48x
If there is more than one answer, separate them with commas. Select "None" if applicable.
Part: 0/2
Part 1 of 2
Zero(s) of k:
Answers
The zeroes of the function k(x)=15x³-48x²-48x are 0, 4 and -4/5.
The function provided is a cubic polynomial.
There will be three zeroes in total for the function k(x).
K(x) = 15x³-48x²-48x
If we put x = 0,
We can see that k(x) becomes zero,
So we can say that 0 is a solutions for this function,
Now,
K(x) = x(15x²-48x-48)
Solving 15x²-48x-48 seperately using quadratic formula,
a = 15
b = -48
c = -48
x = (-b+√D)/D and (-b-√D)/D
D = b²-4ac.
D = (-48)²-4(15)(-48)
D= 5184.
√D = 72
putting all the values to find x,
x = (-(-48)+72)/30 and (-(-48)+72)/30
x = 4 and -4/5.
our function becomes,
k(x) = x(x-4)(x+4/5)
so the zeroes are 0, 4, -4/5.
To know more about cubic polynomial, visit,
https://brainly.com/question/1417425
#SPJ9
The density of water is: Question 3 options: 1g/ml 5g/ml 10g/ml 1000g/ml
Answers
Answer:
1000g/ml is the approximate density of water.
Step-by-step explanation:
Hope it helps!
Answered by
\(ROSALIND\)
What is the radius and diameter of the following circle?

Answers
Answer:
Radius=9
Diameter=18
Step-by-step explanation:
Consider a continuous-time random process, X(t), obtained as the result of a sample-and-hold operation on a noise voltage V(t). IT can be expressed analytically asX(t) = \sum_{n = - \infty }^{\infty} V(nT)h(t- nT)where T is the sampling period and h(t) is the holding pulse,h(t) = 1 \: \: \: \: \: \: 0\leq t \leq Tandh(t) = 0 \: \: \: \: \: \: otherwise
Assume that V(nT) is zero-mean for all n.
Assume that V(nT) has variance\sigma _{v}^{2}for all n.
Assume that T is large enough to render V(nT) and V([n+k]T) statistically independent for all n and for all k\neq0.
A. Find the autocorrelation of X(t).
Answers
The holding pulse is nonzero only for\(0 \leq t \leq T\), the autocorrelation of X(t) is given by\begin{align}
\(R_{xx}(t,t+\tau) =\)
\(\begin{cases}\sigma_v^2 \sum_{n=-\infty}^{\infty}\sum_{m=-\infty}^{\infty}h(t-nT)h(t+\tau-mT) & 0 \leq \tau \leq T \\0 & \text{otherwise}.\end{cases}\end{align}\)
The autocorrelation of X(t) is defined as\(R_{xx}(t,t+\tau) = E[X(t)X(t+\tau)]\)where E[.] is the expectation operator. Since V(nT) has zero mean and is statistically independent, we can write
\(R_{xx}(t,t+\tau) &= E[X(t)X(t+\tau)]\\ &= E\left[\sum_{n=-\infty}^{\infty}V(nT)h(t-nT)\sum_{m=-\infty}^{\infty}V(mT)h(t+\tau-mT)\right]\\&= \sum_{n=-\infty}^{\infty}\sum_{m=-\infty}^{\infty}E[V(nT)V(mT)]h(t-nT)h(t+\tau-mT)\\&= \sigma_v^2 \sum_{n=-\infty}^{\infty}\sum_{m=-\infty}^{\infty}h(t-nT)h(t+\tau-mT)\end{align}\)
Since the holding pulse is nonzero only for\(0 \leq t \leq T\), the autocorrelation of X(t) is given by\begin{align}
\(R_{xx}(t,t+\tau) =\)
\(\begin{cases}\sigma_v^2 \sum_{n=-\infty}^{\infty}\sum_{m=-\infty}^{\infty}h(t-nT)h(t+\tau-mT) & 0 \leq \tau \leq T \\0 & \text{otherwise}.\end{cases}\end{align}\)
Learn more about autocorrelation here:
https://brainly.com/question/29342466
#SPJ4
A machine is used to fill bags with a popular brand of trail mix. The machine is calibrated so the distribution of the weights of the bags of trail mix is normal, with mean 240 grams and standard deviation 3 grams. Of the following, which is the least weight of a bag in the top 5 percent of the distribution?
answer choices
a. 234 grams
b. 240 grams
c. 243 grams
d. 246 grams
e. 248 grams
Answers
Answer: A: 234 grams
Step-by-step explanation:
The top five percent of the distribution's lowest weight as calculated from the given data for a bag is 246.
What is Z-score?In statistics, the standard score is the number of standard deviations by which the value of a raw score is above or below the mean value of what is being observed or measured. Raw scores above the mean have positive standard scores, while those below the mean have negative standard scores.
Here, we have,
Average population = 240
Standard deviation for the population; 3
Z-score can be calculated as ,
z = (x' - μ)/σ
The two z-score tables are as follows:
Positive Z Score Table: The observed value is greater than the average of all values.
An observed value that is below the mean of all values is shown by a negative Z score table.
Now, in order to determine which of the top 5 values in the distribution has the least weight, we will use the significance threshold of 1 - 0.05/2 = 0.025.
Z-score is 1.96 at significance level 0.025.
Thus;
1.96 = (x' - 240)/3
3 × 1.96 = x' - 240
x' = 240 + 5.88
x' = 245.88
Getting close to a whole number results ,
x' = 246
Hence, The top five percent of the distribution's lowest weight as calculated from the given data for a bag is 246.
To learn more about z-score
brainly.com/question/25638875
#SPJ2
Consider the following frequency distribution.
Number of Minutes Frequency
0 to less than 5 6
5 to less than 10 9
8 to less than 13 14
13 to less than 18 2
Which rule for constructing a frequency distribution using grouped quantitative data has been violated?
A. Use mutually exclusive classes.
B. Use equal-size classes.
C. Avoid empty classes.
D. No rule has been violated.
Answers
Answer:
A. Use mutually exclusive classes.
Step-by-step explanation:
From the given frequency distribution:
\(\left|\begin{array}{c|c}$Number of Minutes &$Frequency\\-------&------\\$0 to less than 5 &6\\$5 to less than 10& 9\\$8 to less than 13 &14\\$13 to less than 18 &2\end{array}\right|\)
We can see that we have these class interval
5 to less than 108 to less than 13The data in these two ranges will overlap and therefore violates the rule of mutual exclusivity.
tristians parents bought a new house that was 2255 square fee. the price per square foot was 98 dollars. How much did they pay for the house
Answers
Answer:
$220,990
Step-by-step explanation:
Answer:
Step-by-step explanation:
220,990
An ice cream shop has a sign in the shape of an ice cream cone. The sign is made using a semicircle and a triangle, as modeled below.
Which is the best estimate of the area of the sign in square inches?

Answers
Answer: 50in²
Step-by-step explanation:
The area of the ice cream cone will be equal to 50.13 square inches.
What is an area?The space occupied by any two-dimensional figure in a plane is called the area. The space occupied by the semicircle in a two-dimensional plane is called the area of the semicircle.
The space occupied by the triangle in a two-dimensional plane is called the area of the triangle.
Given that the diameter of the semicircle is 6 inches and the height of the triangle is 12 inches.
The area of the cone will be calculated as,
A = Area of semicircle + Area of triangle
A = (1/2)πr² + (1/2) x B x H
A = (1/2) π (3)² + (1/2) x 12 x 6
A = 14.137 + 36
A = 50.13 square inch
Therefore, the area of the ice cream cone will be equal to 50.13 square inches.
To know more about an area follow
https://brainly.com/question/28876142
#SPJ2
Find the z-score separating the lowest 9% of scores from the highest score of 91%
Answers
Answer:
I'm not sure of my answer but try this:
Find the 60th term of the following sequence.
8, 16, 24. ...
Answers
Answer:
Step-by-step explanation:
Remark
You want the 60th term of the arithmetic (?) sequence given.
Formula
L = a + (n - 1)*d
Givens
L = ?
a = 8
d = 8
n = 60
Solution
L = 8 + (60 - 1)*8
L = 8 + 60*8 - 8
L = 480
Answer
The 60th term is 480
Answer:
Step by step explanation :
As we know
\(\:\bf\boxed{an\:=\:a\:+\:(n\:-\:1)\:d}\)
where,
an = the nth term in the sequence
n = the term
d = common difference
a = first term of the AP.
Here,
an = a60
n = 60
d = 16 - 8 = 8
a = 8
Now,
\(\:\mathsf{a60\:=\:8\:+\:(60\:-\:1)(8)}\)
=> \(\:\mathsf{a60\:=\:8\:+\:(59)(8)}\)
=> \(\:\mathsf{a60\:=\:8\:+\:472}\)
=> \(\:\bf{a60\:=\:480}\)
Therefore the 60th term of the AP is 480.
2.2 2.1.4 a Given that A and B are complementary angles and 7 cos A-3 = 0. Determine WITHOUT the use of a calculator, the value of: 7 cos B-3 tan A. (4)
Answers
Which unit of measurement would be the most appropriate to measure a bottle of nail polish
Answers
Answer:
milliliter
Step-by-step explanation:
Most of nail polish have their measurement in ml
A coral reef grows 0.12 minutes every week. How much does it grow in 8 weeks?
Answers
Answer:
0.96
Step-by-step explanation:
0.12 x 8 = 0.96
Which of the following statements contain a variable
Answers
Answer:
ETMNDYRHFNY XYVVNBJRNB
Step-by-step explanation:
EWRVXZ4ES6TE
A kitten's mass at birth was 0.09 kilogram. The kitten gained approximately 0.084 kilogram
each week. After how many weeks is the kitten's mass 1.098 kilograms?
A. 6
B. 12
C. 13
D. 25
Answers
Given rhombus QRST, find the
perimeter if QU = 3 and RU equals 4.
Q
R
T
U
X
S

Answers
The perimeter of the rhombus in this problem is given as follows:
19.8 units.
What is the perimeter of a polygon?The perimeter of a polygon is given by the sum of all the lengths of the outer edges of the figure, that is, we must find the length of all the edges of the polygon, and then add these lengths to obtain the perimeter.
The diagonal length can be obtained as follows:
QU = US = 3.RU = UT = 4.RU + UT = 7.
Applying the Pythagorean Theorem, the side length is obtained as follows:
x² + x² = 7²
2x² = 49
\(x = \sqrt{\frac{49}{2}}\)
x = 4.95.
Then the perimeter is given as follows:
P = 4 x 4.95
P = 19.8 units.
More can be learned about the perimeter of a polygon at https://brainly.com/question/3310006
#SPJ1
Mr bailey plans to plant soybeans in 4 of every 9 acres This year he plans to farm 2,100 acres what is a reasonable estimate of the numbers of acres on which he will plant soybeans
A.60 B. 230 C.520 D.930
Answers
Option D, which is the closest choice to 933.33, is 930. As a result, 930 fraction acres is a plausible estimate of the amount of acres on which Mr. Bailey will plant soybeans
what is fraction?A fraction is a number that represents a portion of a whole or a ratio between two quantities in mathematics. It is represented as a top number (numerator) over a bottom number (denominator) divided by a horizontal line, also known as a vinculum. The fraction 3/4, for example, represents three-quarters of a whole that has been divided into four equal parts. Proper fractions, improper fractions, and mixed numbers are all ways to express a fraction. A suitable fraction is one in which the numerator is less than the denominator, for example, 2/5.
Mr. Bailey intends to plant soybeans on 4 of every 9 acres, which equates to (4/9) of the total acres he farms.
If he intends to cultivate 2,100 acres, the number of acres planted with soybeans is:
(4/9) x 2,100 = 933.33
We must round this amount to the next whole number because he cannot plant soybeans on a fraction of an acre.
Option D, which is the closest choice to 933.33, is 930. As a result, 930 acres is a plausible estimate of the amount of acres on which Mr. Bailey will plant soybeans.
To know more about fraction visit:
https://brainly.com/question/10354322
#SPJ1
What is the value of the expression when a = 5 and b = 2?
Answers
3(y+1/4)>3/4 determine the value of y for the inequality
Answers
Therefore, the solution to the inequality 3(y + 1/4) > 3/4 is y > 0.
What is inequality?An inequality is a mathematical statement that shows a relationship between two values, which are not necessarily equal. Inequalities are represented using symbols such as > (greater than), < (less than), ≥ (greater than or equal to), and ≤ (less than or equal to). Inequalities are commonly used in algebra and other areas of mathematics, as well as in real-world applications such as finance, economics, and science. They can be used to represent constraints or limits on a variable, such as the maximum or minimum value that it can take.
Here,
We can solve the inequality 3(y + 1/4) > 3/4 by first distributing the 3 to the expression inside the parentheses:
3y + 3/4 > 3/4
Next, we can simplify by subtracting 3/4 from both sides:
3y > 0
Finally, we can solve for y by dividing both sides by 3:
y > 0/3
y > 0
To know more about inequality,
https://brainly.com/question/30238773
#SPJ1
Above are two different models of the same rectangular hallway. If the length of the model on the top is 6 cm, what is the length of the model on the bottom?
Answers
Answer: 15cm
Step-by-step explanation: If the length of the model on the top is 6 cm, then the length of the model on the bottom must be 15 cm
A 30-ounce box of cereal contains 12 servings.
Which value represents the unit rate in this scenario?
O A. 0.4 ounces/serving
O B. 2.5 ounces/serving
O c. 6 ounces/serving
O D. 18 ounces/serving
Answers
Answer:
tha answer is B
Step-by-step explanation:
100 multiply by 600 + 1000000=
Answers
Answer:
1060000
Step-by-step explanation:
just calculation does the job
Answer:
100 x 600=60,000 + 1,000,000= 1,060,000
Step-by-step explanation:
you take the 2 zeros after 100 and add them to the 600 then just add
hope this helps
The radius of a circle is 5 meters. What is the length of a 45° arc?
Answers
Answer:
Step-by-step explanation:

will mark brainleist pls help

Answers
Answer:
x = 31°
Step-by-step explanation:
the sum of the 3 angles in a triangle = 180° , that is
x + 54° + 95° = 180°
x + 149° = 180° ( subtract 149° from both sides )
x = 31°
Pls help me I am stuck tysm

Answers
a) The initial deposit in the account is given as follows: 1,287.39 euros.
b) The interest rate of the account is given as follows: 3%.
How to obtain the balance using simple interest?The equation that gives the balance of an account after t years, considering simple interest, is modeled as follows:
A(t) = P(1 + rt).
In which the parameters of the equation are listed and explained as follows:
A(t) is the final balance.P is the value of the initial deposit.r is the interest rate, as a decimal.t is the time in years.Considering the balances after 5 and 6 years, the interest rate is obtained as follows:
r = 1524.60/1480.50 - 1
r = 0.03.
Considering the balance after 5 years, the initial deposit is obtained as follows:
P(1 + 0.03 x 5) = 1480.5
P = 1480.5/1.15
P = 1,287.39 euros.
More can be learned about simple interest at https://brainly.com/question/20690803
#SPJ1
Manny has an investment account that compounds interest continuously at a rate of 3.1%. After 2 years, he has $7500 in the account. How much money did he initially place in the account? Round your answer to the nearest dollar.
Answers
75=PE^0.062
P=7500/E^0.062
P=7500/1.063962345
P=7049.121649
P=7049
Thus the answer is $7049
Answer:
Step-by-step explanation:
Use the formula for calculating compound interest A=Pert where P is the unknown, A=7500, r=0.031, and t=2.
Because P is the unknown value, solve the initial formula for P by dividing both sides by ert.
A=Pert
Aert=P
Substitute the values into the formula and simplify.
7500e(0.031)(2)=P
7500e0.062=P
7049.1216...=P
Rounded to the nearest whole dollar, P≈7049.
The test scores for a group of students are shown.
60, 69, 79, 80, 86, 86, 86, 89, 90, 100
Calculate the five number summary of the data set? Minimum = First Quartile (Q1) = Median = Third Quartile (Q3) = Maximum = What is the interquartile range (IQR) Which test score is an outlier?
60
69
90
100
Answers
Answer:
Minimum=60
First Quartile(Q1)=79
Median=86
Third Quartile (Q3)=89
Interquartile range (IQR)=10