Answers
Answer: A. Commutative, Distributive
Step-by-step explanation:
From the top going into step 1, they moved things around inside the parenthesis. You can move the order for adding because 2+5 is the same as 5+2 This is the commutative property because commuting means to go somewhere like to commute to work, so the numbers moved
In step 3, from step 2 they distributed the 5. They multiplied the 5 to each of the terms. Whis is the Distribution property
Related Questions
Tre knows that he can mow 3 lawns in two hours. Tre starts mowing on Monday and wants to complete his 20 lawns before Friday. If he wants to work an equal amount each day, how many hours will he have to work each day to mow all 20 lawns? Explain your process.
Answers
Answer: Tre wants to mow 20 lawns in 5 days, so he needs to mow 20/5=<<20/5=4>>4 lawns per day.
If Tre can mow 3 lawns in 2 hours, then he can mow 1 lawn in 2/3=<<2/3=0.67>>0.67 hours.
This means Tre will have to work 4/0.67=<<4/0.67=6>>6 hours each day to mow all 20 lawns. Answer: \boxed{6}.
Step-by-step explanation:
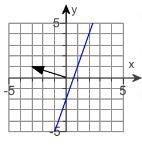
The vector v=ai+bj is perpendicular to the line ax+by=c. Use this fact to find an equation for the line through P perpendicular to v. Then draw a sketch of the line, including v as a vector starting at the origin. P(1,6),v=6i+j
Answers
The equation for the line through P perpendicular to v is y = -6x + 12. The sketch of the line, including v as a vector starting at the origin is attached below:
The vector v is given as v = 6i + j, where i and j are unit vectors in the x and y directions, respectively. This means that the vector v starts at the origin (0,0) and extends 6 units in the x-direction and 1 unit in the y-direction.
The line is given by the equation ax + by = c, where a, b, and c are constants. In this case, the equation of the line is not given, but it is mentioned that the vector v is perpendicular to the line. This means that the line and the vector v are at right angles to each other.
Using this fact, we can find an equation for the line through the point P(1,6) that is perpendicular to the vector v. To do this, we can use the slope-intercept form of a line, y = mx + b, where m is the slope and b is the y-intercept.
Since the line is perpendicular to the vector v, the slope of the line is the negative reciprocal of the slope of v. The slope of v is 1/6, so the slope of the line is -6.
Plugging in the point P(1,6) and the slope -6 into the slope-intercept form, we get the equation
y - 6 = -6(x - 1).
Simplifying this equation gives us
y = -6x + 12.
To visualize this line, we can plot the point P(1,6) on a coordinate plane and draw a line through it with a slope of -6. Additionally, we can draw the vector v starting at the origin and extending 6 units in the x-direction and 1 unit in the y-direction.
To know more about vector visit:
https://brainly.com/question/33923402
#SPJ11
A house owner wishes to cover their roof with solar panels. Each solar panel is of the following size. The roof section is rectangular 7.2 m by 4.4 m. Each solar panel measures 1400 mm by 850 mm. There needs to be at least a 30 cm gap left at each edge of the roof section. The house owner thinks he can have at least 15 solar panels fitted to the roof section. Can u agree? If yes, show the working.
Answers
Answer:
Hello Arjun, The Answer Is 26.54 panels.
Explanation:
Dimensions of roof section: 7.2m By 4.4m
Area Of Roof: 7.2*4.4 = 31.68m²
Dimension of solar panels: 1400mm by 850mm
= 1400÷1000 by 850÷1000 = 1.4m by 0.85m
So We can say that: Area each solar panel = 1.4 * 0.85 = 1.19m²
The 30 CM Gap On All Edges Gives Us A Square Of Side = 30 Cm = 0.3 M
So, The Area Of Gap Left = 0.3*0.3 = 0.9m²
Now, The Total Area That Can Be Covered Is 31.68-0.9 = 31.59m²
So, Now we Divide The area remaining with the area of the solar panel that is: 31.59 ÷ 1.19m² = 26.54 Panels...
I Could Only Understand This Much From The HW Ma'am Gave, So This Was My Answer...
Hope It Helps!
"Write two equations so that each have variables on both sides and a solution of 1/2?
Answers
Let g(x) = 4x - 20 and h(x) = -1/2x + k. For what value of k is the zero of h(x) equivalent to the zero of g(x)
Answers
Answer:
Step-by-step explanation:
The zero of a function is also known as the x-intercept of a function. The x-intercept of a function exists where y = 0. So we will begin by setting each of those lines = 0:
4x - 20 = 0 and -1/2x + k = 0 and then solve each for x:
4x = 20 so
x = 5 and
-1/2x = -k and
1/2x = k so
x = 2k. Now we set the 2 x expressions equal to each other and solve for k:
5 = 2k so
k = 5/2
The value of the K in the given equation is 5/2.
The zero of a function is also known as the x-intercept of a function.
The x-intercept of a function exists where y = 0. So we will begin by setting each of those lines = 0:
4x - 20 = 0 and
-1/2x + k = 0 and then solve each for x:
What is the substitution method?The substitution method is the algebraic method to solve simultaneous linear equations. As the word says, in this method, the value of one variable from one equation is substituted in the other equation.
4x = 20 so
x = 5 and
-1/2x = -k and
1/2x = k so
x = 2k. Now we set the 2 x expressions equal to each other and solve for k
5 = 2k so
k = 5/2
Therefore the value of the K in the given equation is 5/2.
To learn more about the expression visit:
https://brainly.com/question/723406
#SPJ2
Find y.
Round to the nearest tenth:
31°
y
X
400 ft
y = [? ]ft
![Find y.Round to the nearest tenth:31yX400 fty = [? ]ft](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/dAOwZ5551CCyAzV1NN84bFZ42Y2StDWu.png)
Answers
Answer:
y = 240.3 ft
Step-by-step explanation:
Use trigonometric ratio to find y:
Thus,
Reference angle = 90° - 31° = 59°
Opposite = 400 ft
Adjacent = y
Therefore:
Tan 59° = 400/y
Multiply both sides by y
y*tan 59 = 400
Divide both sides by tan 59
y = 400/tan 59
y = 240.3 ft (to the nearest tenth)
On a coordinate plane, a line goes through points (negative 4, 0) and (0, negative 8).
For the graph, locate the x-intercept and the y-intercept.
x-intercept =
y-intercept =
Answers
The x-intercept of the line is: -4.
The y-intercept is: -8
What is the X-intercept and the Y-intercept of a Line?The y-intercept of a line is the point where the line cuts across the y-axis (vertical axis), which is the value of y when x is zero.
The x-intercept of a line is the point where the line cuts across the x-axis (horizontal axis), which is the value of y when x is zero.
Given that a line passes through (-4, 0) and (0, -8), it means that:
The line cuts the y-axis at y = -8
The line cuts the x-axis at x = -4.
Therefore, we can state that the y-intercept of the line is -8, while the x-intercept of the line is -4.
Learn more about the x- and y-intercepts of a line on:
https://brainly.com/question/18702279
#SPJ1
Calculate the 95% confidence interval for the following fictional data regarding daily TV viewing habits: µ = 4.7 hours; = 1.3 hours; sample of 78 people with a mean of 4.1 hours.
1) What are the z cutoffs for the 95% confidence level?
2) What is the standard error?
3) What is the upper bound?
4) What is the lower bound?
5) State the confidence interval using brackets []
Answers
The required answers are:
1) The z cutoffs for the 95% confidence level is \(^+_- 1.96\)
2) The standard error is 0.147.
3) The upper bound is 4.393.
4) The lower bound is 3.807.
5) The confidence interval for the fictional data regarding daily TV viewing habits is [3.807, 4.393] hours
To calculate the 95% confidence interval, we can follow these steps:
1) Find the z cutoffs for the 95% confidence level:
The z-cutoffs represent the number of standard deviations away from the mean that encloses the desired confidence level. For a 95% confidence level, we need to find the z-value that encloses 95% of the area under the standard normal distribution.
Using a standard normal distribution table or a calculator, we will find that the z-value for a 95% confidence level is approximately \(^+_-1.96\).
2) Calculate the standard error (SE):
The standard error measures the variability of the sample mean. It is calculated using the formula: SE = \(\sigma/\sqrt{n}\), where \(\sigma\) is the population standard deviation and n is the sample size.
In this case, the population standard deviation is unknown, but we can estimate it using the sample standard deviation. Since the sample standard deviation (s) is not provided, we'll use the population standard deviation (\(\sigma\)) given in the fictional data.
The standard error (SE) = \(\sigma/\sqrt{n} = 1.3/\sqrt{78} = 0.147\)
3) Calculate the upper bound:
The upper bound of the confidence interval is calculated as upper bound = sample mean + (z-value * SE).
Upper bound = 4.1 + (1.96 * 0.147) = 4.393
4) Calculate the lower bound:
The lower bound of the confidence interval is calculated as lower bound = sample mean - (z-value * SE).
Lower bound = 4.1 - (1.96 * 0.147) = 3.807
5) State the confidence interval using brackets []:
The confidence interval is typically stated as an interval with the lower bound and upper bound values enclosed in brackets [].
Confidence interval: [3.807, 4.393]
Therefore, the 95% confidence interval for the fictional data regarding daily TV viewing habits is [3.807, 4.393] hours.
Learn more about standard deviation at:
https://brainly.com/question/24298037
#SPJ4
C. 2 Use Simplex tableau method to solve the following linear programming problem:
maximize = 2x1 + 5x2 + 4x3
subject to x1 +x2 + 2x3≤ 20
2x1 + x2 + x3 ≤ 10
x2 − x3 ≤ 5
3x1 +3x3 ≤ 12
x1,x2,x3 ≥0
Answers
New Simplex Tableau:
| Basis | x1 | x2
To use the simplex tableau method to solve the given linear programming problem, we need to convert it into standard form. The standard form includes non-negativity constraints and all inequalities as less than or equal to constraints. Let's rewrite the problem in standard form:
Maximize: Z = 2x1 + 5x2 + 4x3
Subject to:
x1 + x2 + 2x3 + x4 = 20
2x1 + x2 + x3 + x5 = 10
0x1 + x2 - x3 + x6 = 5
3x1 + 0x2 + 3x3 + x7 = 12
x1, x2, x3, x4, x5, x6, x7 ≥ 0
Now, let's construct the initial simplex tableau:
Basis x1 x2 x3 x4 x5 x6 x7 RHS
x4 1 1 2 1 0 0 0 20
x5 2 1 1 0 1 0 0 10
x6 0 1 -1 0 0 1 0 5
x7 3 0 3 0 0 0 1 12
Z -2 -5 -4 0 0 0 0 0
Next, we will perform iterations to find the optimal solution. The goal is to make the coefficients in the Z row non-negative. We will select the most negative coefficient as the pivot column and the smallest ratio of the RHS to the pivot column value as the pivot row.
Iteration 1:
Pivot Column: x2 (most negative coefficient)
Pivot Row: x6 (smallest ratio of RHS / pivot column value)
Perform row operations to make x6 a basic variable:
Row 3 = Row 3 / 1
Perform column operations to clear the pivot column:
Row 1 = Row 1 - 1 * Row 3
Row 2 = Row 2 - 1 * Row 3
Row 4 = Row 4 - 0 * Row 3
Row 5 = Row 5 + 5 * Row 3
New Simplex Tableau:
Basis x1 x2 x3 x4 x5 x6 x7 RHS
x4 1 0 3 1 0 0 0 15
x5 2 0 2 0 1 0 0 35
x2 0 1 -1 0 0 1 0 5
x7 3 0 3 0 0 0 1 12
Z -2 0 -3 0 0 5 0 20
Iteration 2:
Pivot Column: x3 (most negative coefficient)
Pivot Row: x4 (smallest ratio of RHS / pivot column value)
Perform row operations to make x4 a basic variable:
Row 1 = Row 1 - 3 * Row 4
Row 2 = Row 2 - 2 * Row 4
Row 3 = Row 3 - (-1) * Row 4
Row 5 = Row 5 - 3 * Row 4
Perform column operations to clear the pivot column:
Row 2 = Row 2 - 2 * Row 5
Row 1 = Row 1 - 3 * Row 5
Row 3 = Row 3 - (-1) * Row 5
Row 7 = Row 7 - 0 * Row 5
New Simplex Tableau:
| Basis | x1 | x2
Learn more about Simplex Tableau from
https://brainly.com/question/31400001
#SPJ11
Hey guys could someone please help me?
THANKS SO MUCH!

Answers
Answer:
your answer is |||. hope that helps.
What is the Area of the Hexagon?
Answers
The region included by a hexagon's sides is known as the area of the hexagon.
What is a hexagon?
A hexagon is a two-dimensional shape with six sides, six angles, nine diagonals, and a total of 720 degrees in its inner angles.
The space included within the polygon's sides is referred to as the hexagon's area.
The area of a regular hexagon is calculated using the formula
(3√3s^2)/2, where 's' is the length of a hexagonal side.
The fact that all the sides are the same length should be noted since we are discussing a regular hexagon.
Hence, area of hexagon is the region included by a hexagon's sides.
Learn more about hexagon from the given link
https://brainly.com/question/30384520
#SPJ4
what is the volume of the solid generated when the region in the first quadrant bounded by the graph of y=x3, the y-axis, and the horizontal line y=1 is revolved about the y-axis?
Answers
The volume of the solid is 4/5π.
The volume of a solid generated by revolving a region around a line is given by V = ∫a b π(y)2dy, where a and b are the lower and upper limits of the region, respectively, and y is a function of x.
In this case, the region is bounded by the graph of y=x3, the y-axis, and the horizontal line y=1. Therefore, the volume of the solid generated when the region is revolved about the y-axis is given by
V = ∫0 1 π(y)2dy
= ∫0 1 πx6dx
= π/7
= 4/5π
The volume of the solid is calculated using the formula V = ∫a b π(y)2dy, where a and b are the lower and upper limits of the region and y is a function of x. In this case, the lower limit is a=0 and the upper limit is b=1, since the region is bounded by the graph of y=x3, the y-axis, and the horizontal line y=1. Integrating from a=0 to b=1 gives the volume of the solid as V = ∫0 1 πx6dx = π/7 = 4/5π.
Learn more about volume here
https://brainly.com/question/16134180
#SPJ4
the correlation coefficient may assume any value between : -1, and 1. 0 and 1. 0 and 8. -1, and 0. -infinity and infinity.
Answers
The correlation coefficient may assume any value between -1 and 1. Correct answer option A.
This means that the coefficient might be negative, zero, or positive, with -1 being a perfect negative correlation, 0 representing no connection, and 1 representing a perfect positive correlation.
The correlation coefficient is a numerical measure of two variables' linear connection. It is a measure of the strength of the link between two variables. A correlation coefficient of 1 indicates that there is a perfect positive connection, a coefficient of -1 indicates that there is a perfect negative correlation, and a coefficient of 0 shows that there is no correlation between the two variables.
Learn more about correlation coefficient:
brainly.com/question/12663699
#SPJ4
Please help please please
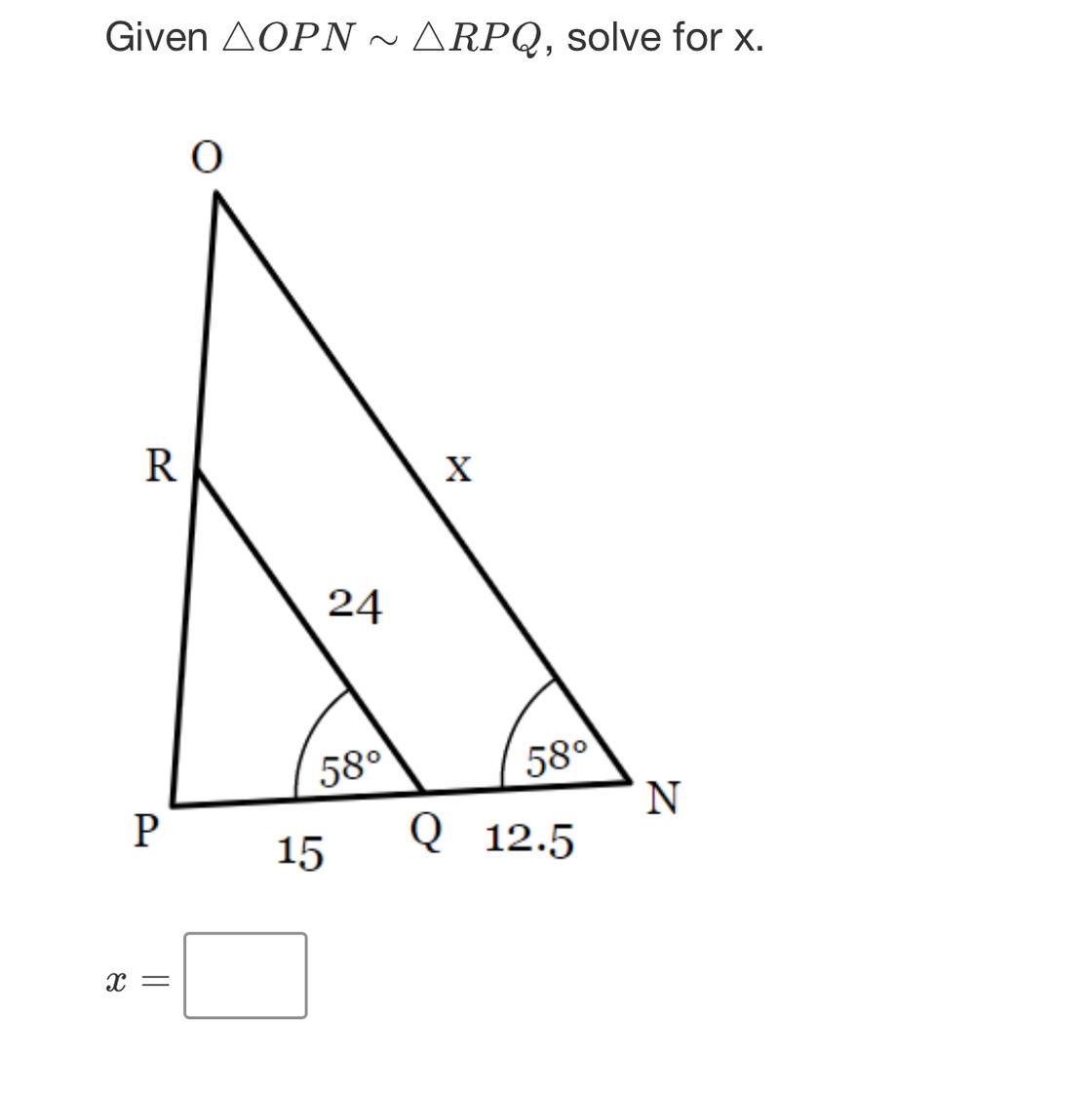
Answers
Answer: 44
Step-by-step explanation:
since OPN and RPQ are similar triangles, you can use ratios to find their sides
\(\frac{24}{15} =\frac{x}{15+12.5}\) or \(\frac{24}{15} =\frac{x}{27.5}\)
cross multiply to get: 24*27.5 = 15x
660/15 = x
x = 44
IF you add 6 tens of thousands, 5 thousands and 3 hundreds together what is the value of the largest digit of the answer?
Answers
Answer:
ten thousands place
Step-by-step explanation:
6 tens of thousands = 60,000
5 thousands= 5,000
3 hundreds= 300
60,000
+ 5,000
+ 300
65,300
determine whether the sequence converges or diverges. if it converges, find the limit. (if an answer does not exist, enter dne.) an = 4 5n2 n 4n2 lim n→[infinity] an =
Answers
The sequence diverges and does not have a finite limit as n approaches infinity.
To determine if the sequence converges or diverges, we will analyze the given sequence, \(a_n = (4 \cdot 5n^{2} \cdot n) / (4n^{2})\). We can simplify this sequence and find the limit as n approaches infinity.
First, simplify the sequence:
\(a_n = (4 \cdot 5n^2 \cdot n) / (4n^{2})\\ a_n = (20n^{3}) / (4n^{2})\)
Next, cancel out the common terms:
\(a_n = 5n\)
Now, to find the limit as n approaches infinity:
lim n→∞ (5n)
Since the sequence contains a linear term "5n" without any restrictions, as n approaches infinity, the sequence will also approach infinity. This means the sequence does not have a finite limit and therefore diverges. In this case, we can represent the limit as:
lim n→∞ \(a_n\) = ∞
In conclusion, the sequence \(a_n = 5n\) diverges and does not have a finite limit as n approaches infinity.
Learn more about divergence here:
https://brainly.com/question/30726405
#SPJ11
find the median of data set: 23, 31, 32, 34, 39, 38, 38, 34, 38
Answers
Answer: 34
Hope this helps :)
If point A is located at (5, –3) and point B is located at (–4, –6). Find AB A B rounded to the nearest tenth.
Answers
The distance between the point A and point B is 9.5 units
Distance between two pointsThe formula for calculating the distance between two points is expressed according to the formula shown below;
AB = √(x₂-x₁)²+(y₂-y₁)²
Using the given coordinates points A(5, -3) and B (-4, -6)
Substitute to have:
AB = √(5-(-4))²+(-3-(-6))²
AB = √(5+4)²+(-3+6))²
AB = √81+9
AB = √90
AB = 9.5 units
Hence the distance between the point A and point B is 9.5 units
Learn more on distance between points here: https://brainly.com/question/24775607
#SPJ1
Which system models this situation? y = 26x and y = 8,400(x-500)2 15,900 y = 26x and y = -0.030(x-500)2 15,900 y = x/26 and y = -0.030(x-500)2 15,900 y = x/26 and y =8,400(x-500)2 15,900
Answers
The option B is a correct option which is y = 26x and y = -0.030(x-500)2 15,900 represent the quadratic and linear function.
According to the statement
we have given that Vertex
(h,k) = (500, 15900)
And One of the points on the graph
(x,y) = (0,8400)
FIRST PART: we have to find the quadratic function
We can find the quadratic function by parabola's equation formula
y = a (x - h)² + k -(1)
Input the numbers to the formula, to find the value of a
y = a (x - h)² + k
8400 = a(0 - 500)² + 15900
8400 = a (500)² + 15900
8400 = 250000a + 15900
-250000a = 15900 - 8400
-250000a = 7500
a = 7500/-250000
a = 0.03
Now,
Submit a to the formula (1)
y = a (x - h)² + k
y = 0.03 (x - 500)² + 15900
this is the quadratic equation.
SECOND PART: Find the linear function
the total cost = cost each helmet × the number of helmet
y = 26x
So,
The option B is a correct option which is y = 26x and y = -0.030(x-500)2 15,900 represent the quadratic and linear function.
Learn more about quadratic and linear function here https://brainly.com/question/25841119
Disclaimer: This question was incomplete. Please find the full content below.
Question: A company plans to sell bicycle helmets for $26 each. The company's business manager estimates that the cost, y, of making x helmets is a quadratic function with a y-intercept of 8,400 and a vertex of (500, 15900)
x= number of helmets
y = amount in dollars
Which system models this situation?
a) y = 26x and y = 8,400(x-500)2+15,900
b) y = 26x and y = -0.030(x-500)2+15,900
c) y = x/26 and y = -0.030(x-500)2+15,900
d) y = x/26 and y =8,400(x-500)2+15,900
#SPJ4
Answer:
B. y = 26x and y = -0.030(x-500)2+15,900
Step-by-step explanation:

Whats the slope form?

Answers
Answer:
The slope form would be 2/3x-6
Answer:
y=2/3x-6
Step-by-step explanation:
Slope intercept form is y=mx+b. m is your slope or rise/run (rise-over-run). This line rises 2 and runs 3 so your slope is 2/3. b is your y-intercept. This line intercepts y at -6 so b=-6. Therefore your equation is y=2/3x-6. Hope this helped!
the nurse observes dappled brown patches inside on a patient’s cheek. what does this indicate?
Answers
The presence of dappled brown patches on a patient's cheek may indicate a condition called melasma. Melasma is a common skin condition that typically affects women and is associated with hormonal changes, sun exposure, and genetic factors.
Dappled brown patches on the cheek often suggest a condition called melasma. Melasma is a common skin disorder characterized by the development of dark, irregularly shaped patches on the skin. It typically affects women, especially those with darker skin tones, and is often associated with hormonal changes, such as during pregnancy or with the use of birth control pills. Sun exposure is another contributing factor to the development of melasma. Genetic factors also play a role, as it tends to run in families. Melasma is not a harmful or dangerous condition but can cause cosmetic concerns and affect a person's self-esteem.
To manage melasma, various treatment options are available. These include topical creams containing ingredients such as hydroquinone, tretinoin, or corticosteroids, which can help lighten the patches over time.
Chemical peels that involve the application of a chemical solution to exfoliate the skin and reduce hyperpigmentation may also be used. In some cases, laser therapy can be beneficial to target and break up the excess pigment in the affected areas.
It's important to note that melasma may recur, especially with sun exposure, so it's essential to protect the skin from the sun by wearing sunscreen and using protective clothing. Consulting a dermatologist is recommended to determine the most appropriate treatment approach for an individual case of melasma.
Learn more about Factors:
brainly.com/question/26923098
#SPJ11
(a) Find a cubic function P(t) that models these data, where P is the U.S. population in millions and t is the number of years past 1950. Report the model with three significant digit coefficients.(b) Use the part (a) result to find the function that models the instantaneous rate of change of the U.S. population.(c) Find and interpret the instantaneous rates of change in 2000 and 2025.
Answers
(a) cubic function with three significant digit coefficients: P(t) = 150.7 + 0.358t - 0.000219t^2 + 0.0000012t^3.
(b) function that models the instantaneous rate of change of the U.S. population : P'(t) = 0.358 - 0.000438t + 0.0000036t^2
(c) So, in 2000, the U.S. population was growing at a rate of 0.168 million people per year, and in 2025 it will be growing at a rate of 0.301 million people per year.
(a) To model the U.S. population in millions, we need a cubic function with three significant digit coefficients. Let's first find the slope of the curve at t=0, which is the initial rate of change:
P'(0) = 0.358
Now, we can use the point-slope form of a line to find the cubic function:
P(t) - P(0) = P'(0)t + at^2 + bt^3
Plugging in the values we know, we get:
P(t) - 150.7 = 0.358t + at^2 + bt^3
Next, we need to find the values of a and b. To do this, we can use the other two data points:
P(25) - 150.7 = 0.358(25) + a(25)^2 + b(25)^3
P(50) - 150.7 = 0.358(50) + a(50)^2 + b(50)^3
Simplifying these equations, we get:
P(25) = 168.45 + 625a + 15625b
P(50) = 186.2 + 2500a + 125000b
Now, we can solve for a and b using a system of equations. Subtracting the first equation from the second, we get:
P(50) - P(25) = 17.75 + 1875a + 118375b
Substituting in the values we just found, we get:
17.75 + 1875a + 118375b = 17.75 + 562.5 + 15625a + 390625b
Simplifying, we get:
-139.75 = 14000a + 272250b
Similarly, substituting the values we know into the first equation, we get:
18.75 = 875a + 15625b
Now we have two equations with two unknowns, which we can solve using algebra. Solving for a and b, we get:
a = -0.000219
b = 0.0000012
Plugging these values back into the original equation, we get our cubic function:
P(t) = 150.7 + 0.358t - 0.000219t^2 + 0.0000012t^3
(b) To find the function that models the instantaneous rate of change of the U.S. population, we need to take the derivative of our cubic function:
P'(t) = 0.358 - 0.000438t + 0.0000036t^2
(c) Finally, we can find the instantaneous rates of change in 2000 and 2025 by plugging those values into our derivative function:
P'(50) = 0.358 - 0.000438(50) + 0.0000036(50)^2 = 0.168 million people per year
P'(75) = 0.358 - 0.000438(75) + 0.0000036(75)^2 = 0.301 million people per year
So in 2000, the U.S. population was growing at a rate of 0.168 million people per year, and in 2025 it will be growing at a rate of 0.301 million people per year. This shows that the population growth rate is increasing over time.
Know more about the cubic function
https://brainly.com/question/20896994
#SPJ11
Alberto started out bench pressing 60 pounds. He then added 5 pounds every week. Determine whether the situation is linear or nonlinear, and proportional or nonproportional
Answers
Answer
linear
nonproportional
Step-by-step explanation:
Since for each equal change in time (1 week), there is an equal change in weight (5 lb), the situation is linear.
At time zero, the first week, the weight was not zero. It was 60 lb, so it is not proportional.
Answer:
linear
nonproportional
Pls help due ASAP
Show workings please!!!

Answers
Answer:
AB=8
Step-by-step explanation:
First, you get figure out x. Since both sides are equal, use the equation x+3=2x-2, then subtract x from both sides, 3=x-2, and then add 2 to both sides, x=5. Then use one of the equations to get the length of the side, I used x+3=8, which is your answer.
(hope this helps :P)
He remembers that the slope of the line through the ordered pairs in the table was 4. What is the missing y-value in the table?
Answers
Answer:
i think it is 7 i just looked it up but it might be accurate
any more help just ask :)
the diameter of small nerf balls manufactured overseas is expected to be approximately normally distributed with a mean of 5.2 inches and a standard deviation of .08 inches. suppose a random sample of 20 balls is selected. find the interval that contains 95.44 percent of the sample means.
Answers
The interval that contains 95.44 percent of the sample means is between 5.1642 inches and 5.2358 inches
Normal probability distribution
Problems of normally distributed samples are solved using the z-score formula.
In a set with mean and standard deviation , the zscore of a measure X is given by:
Z = X-u/σ
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.
Central Limit Theorem
The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean and standard deviation , the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean u and standard deviation s=σ/\(\sqrt{n}\)
For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.
In this problem, we have that:
u= 5.2 ,σ = 0.08 , n= 20 s= 0.0179
Find the interval that contains 95.44 percent of the sample means.
0.5 - (0.9544/2) = 0.0228
Pvalue of 0.0228 when Z = -2.
0.5 + (0.9544/2) = 0.9772
Pvalue of 0.9772 when Z = 2.
So the interval is from X when Z = -2 to X when Z = 2
Z = 2
Z= X-u/σ
By the central Limit Theorem
Z= X-u/s
X= 5.2358
Z = -2
then
X= 5.1642
learn more about of interval here
https://brainly.com/question/9035934
#SPJ4
t-models, part II Using the t tables, software, or a calculator, estimate
a) the critical value of t for a 95% confidence interval with df = 7.
b) the critical value of t for a 99% confidence interval with df = 102.
Answers
The critical value of t with df as 7 is 2.36, and the critical value of t with df as 102 is 2.62
In a hypothesis test, the critical value is a value that is used to decide whether to accept the null hypothesis or not. It is based on the level of significance that was selected, which is the highest likelihood that a Type I error could occur.
a)
On referring to the t-distribution table, which is statistical software, or a calculator to find the critical value of t for a 95% confidence interval with degrees of freedom (df) = 7. The two-tailed confidence level of 0.95 is the essential value. We discover that the crucial value of t for a 95% confidence interval with df = 7 is roughly 2.365 using a t-distribution table or program.
b)
The t-distribution table, statistical software, or a calculator are used in a similar manner to estimate the critical value of t for a 99% confidence interval with df = 102. The crucial value is equal to the 0.99 two-tailed confidence level. The crucial value of t for a 99% confidence interval with df = 102 is roughly 2.62, according to a t-distribution table or computer programme.
Read more about critical value on:
https://brainly.com/question/31529419
#SPJ4
To prove that the triangles are similar by the sss similarity theorem, which other sides or angles should be used? mn and sr mn and qr ∠s ≅ ∠n ∠s ≅ ∠o
Answers
To prove that the triangles are similar by the SSS (Side-Side-Side) similarity theorem, the corresponding sides of the triangles MN and SR must be proportional to each other.
In the SSS similarity theorem, for two triangles to be similar, all three pairs of corresponding sides must be proportional. In the given scenario, we have triangles MN and SR. To establish similarity using the SSS theorem, we need to compare the lengths of the corresponding sides of these triangles.
We are given that MN is proportional to SR, and based on the information provided, we can conclude that QR is proportional to NO.
However, we don't have information about the third pair of sides, which is MN and QR, to establish similarity using the SSS theorem. Therefore, we cannot prove the similarity of these triangles solely based on the given information.
To prove the similarity of triangles MN and SR using the SSS similarity theorem, we also need to compare the lengths of the remaining pair of corresponding sides, MN and QR. Without that information, we cannot establish similarity solely based on the provided sides and angles.
To know more about triangles , Visit :
https://brainly.com/question/31096075
#SPJ11
Three pairs of shoes and two pairs of socks cost $123, while three pairs of socks and two pairs of shoes cost $89.50. What does one pair of socks cost?
Answers
Answer:
$2 I think not sure if not sorry
hospital records show that 12% of all patients are admitted for heart disease, 16% are admitted for cancer (oncology) treatment, and 4% receive both coronary and oncology care. what is the probability that a randomly selected patient is admitted for coronary care, oncology or both? (note that heart disease is a coronary care issue.)
Answers
The probability of randomly selected patient selected for coronary, oncology or both is equal to P( H∪C ) = 0.24.
Let patient admitted with heart disease represented by P(H)
P(H) = 12%
= 0.12
And patient admitted for cancer disease represented by P(C)
P(H) = 16%
= 0.16
Percent of patient received both coronary and oncology = 4%
P( H∩C ) = 0.04
Probability of randomly selected patient admitted for coronary, oncology or both is :
P( H∪C ) = P(H) + P(C) - P(H∩C )
⇒P( H∪C ) = 0.12 + 0.16 - 0.04
⇒ P( H∪C ) = 0.24
Therefore, the probability of randomly selected patient getting treatment for coronary, oncology or both is given by P( H∪C ) = 0.24.
Learn more about probability here
brainly.com/question/11234923
#SPJ4
