Answers
Answer:
Option 2 and Option 5
Step-by-step explanation:
Answer:it is the second one
Step-by-step explanation:
Related Questions
a spinner is divided into four equal sections: two are red, one is green, and one is blue. chris spins the spinner four times in a row, and it lands on green each time. should he suspect that the spinner is broken?
Answers
It is not sufficient evidence to conclude that the spinner is broken. He should not suspect that the spinner is broken
Chris spinning the spinner and getting the green color four times in a row does not necessarily indicate that the spinner is broken. The probability of landing on green on each spin is independent of previous spins, assuming the spinner is fair and unbiased.
To determine if the spinner is broken, we would need to compare the observed results to the expected results based on the known probabilities. In this case, since the spinner has four equal sections (2 red, 1 green, 1 blue), the probability of landing on green on any given spin is 1/4.
The probability of getting green four times in a row, assuming independence, is (1/4) * (1/4) * (1/4) * (1/4) = 1/256, which is a relatively low probability but still possible.
Therefore, based solely on getting green four times in a row, it is not sufficient evidence to conclude that the spinner is broken.
Learn more about probability at https://brainly.com/question/11838874
#SPJ11
PLEASE HELPP MEEE I NEED THE ANDWER QUICKKK
20.00$ - a=8.45$
Answers
Answer:
a= 11.55
Step-by-step explanation:
If the answer is 8.45, then the variable equals the difference of 20 minus the answer, 8.45
Hope this helps!
The perimeter of the tennis court is 228 feet. What are the dimensions of the court? Write the equation for the situation: What is the width of the court? What is the length of the court?
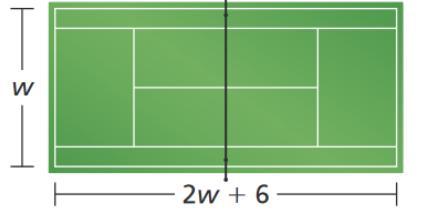
Answers
Answer:
It’s 36 by 78 tennis court
width = 36 ft.
length = 78 ft.
Step-by-step explanation:
2(w+2w+6)=228 feet
2w+4w+12=228
6w=228-12
6w=216
w=36
So, 2w+6=78
It’s 36 by 78 tennis court
width = 36 ft.
length = 78 ft.
The dimensions of the tennis court can be determined by solving the equation system: width (w) = 42 feet and length (l) = 96 feet.
To find the dimensions of the tennis court, we can set up a system of equations based on the given information:
Equation for the perimeter:
The perimeter of a rectangle is given by the formula:
P = 2(length + width).
In this case,
the perimeter is 228 feet, so the equation gives:228 = 2(l + w)
Equation relating length and width: It is stated that the width (w) is equal to the length (l), which can be expressed as:
w = l
To solve the system of equations:
Substitute the value of l from the second equation into the first equation:
\(228 = 2((2w + 6) + w)\)
Simplifying the equation:
\(228 = 2(3w + 6)\)
Divide by 2 on both sides
\(114 = 3w + 6\)
Subtract by 6 on both sides
\(108 = 3w\)
Divide by 3 on both sides
\(w = 36\)
Substituting the value of w back into the second equation:
\(l = 36\)
Therefore, the width of the tennis court is 36 feet, and the length is 96 feet.
Learn more about solving equations here:
https://brainly.com/question/14410653
#SPJ4
-6<3x+12` and 3x+12<21
Answers
Answer:
x>−6 and x<3 which is (-6,3)
Step-by-step explanation:
A refrigerator is priced at $525.50. There is a 6% sales tax rate. What is the sales tax for the refrigerator in dollars and cents?
Answers
Answer:
$31.53
Step-by-step explanation:
I used a calculator
Find the height of the basketball hoop using similarity ratios. Explain step by step.

Answers
The height of the basketball hoop is 13.32'.
What is law of similarity?
The Law of Similarity in mathematics states that if two geometric figures have the same shape but different sizes, then they are considered similar. This means that the corresponding angles of the two figures are congruent, and the corresponding sides are proportional in length.
Formally, if we have two geometric figures A and B, and if every angle of figure A is congruent to the corresponding angle of figure B, and if the ratio of the length of any pair of corresponding sides of A and B is constant, then we can say that A and B are similar figures.
Here we can see two triangle and base of two triangle is given.
Here base of small triangle is 12' and the base of big triangle is (12'+25') = 37'.
It is also given that height of small triangle is 4'3.84".
Now we want to find the height of the basketball hoop which is equal to height of big triangle.
Let the height of the basketball hoop be x.
So, by law of similarity ratios,
12'/37' = 4'3.84"/x
Now, 4'3.84" = 4.32'
So, 12'/37' = 4.32'/x
Therefore, x = 13.32'
Therefore, the height of the basketball hoop is 13.32'.
Learn more about triangle here,
https://brainly.com/question/27827375
#SPJ1
equation of the circle centered at the origin and passing through the point equation of the circle centered at the origin and passing through the point (-4,0)
Answers
The equation of the circle centered at the origin and passing through the point (-4,0) is \(x^2+y^2=16\).
Equation of a circle
A circle may also be defined as a special kind of ellipse in which the two foci are coincident, the eccentricity is 0, and the semi-major and semi-minor axes are equal.
We know that,
Equation of the circle passing through the origin is given by:-
\(x^2+y^2=r^2\)
Where,
r is the radius of the circle, and
(x,y) are the coordinates of each point of the circle.
Hence, we can write,
The radius of the circle will be :-
\(\sqrt{(0-(-4))^2+(0-0)^2} =\sqrt{ 4^2+0^2} =\sqrt{16}=4 units\)
Hence, r = 4 units.
Hence, the equation of the circle is given by:-
\(x^2+y^2=16\)
To learn more about radius, here:-
https://brainly.com/question/15047456
#SPJ4
Tammy and Wyatt are sales associates at the same used car dealership. Their supervisor is planning to promote the employee with the best sales numbers, on average. The box plots below show their sales, in thousands of dollars, for the past two weeks: box plot labeled Tammy with min at 19, Q1 at 21, median at 25. 5, Q3 at 26. 75, max at 27. 75. Box plot labeled Wyatt with min at 18. 5, Q1 at 20. 5, median at 24, Q3 at 27. 5, max at 28. 25 Who should get the promotion, and why? Wyatt should get the promotion. His data is more evenly distributed, so his sales are more consistent. Wyatt should get the promotion because he had the highest sales in a single day. Tammy should get the promotion because her lowest value is higher than Wyatt's lowest value. Tammy should get the promotion. She has a higher median with a smaller IQR, so her sales are better on average.
Answers
The Answer: Tammy should get the promotion. She has a higher median with a smaller IQR, so her sales are better on average.
Help meeeeeeeeeeee PLS ASAP

Answers
Answer:
A
Step-by-step explanation:
Answer:
angle 1 and angle 5
Step-by-step explanation:
The expression 8 x plus 12 y represents the sum of Harry and Mike’s total monthly wages, where x represents the number of hours Harry worked and y represents the number of hours Mike worked. What is another way to write the expression, and what can you conclude from rewriting it in this way?
A. 8 left parenthesis x plus 1.5 y right parenthesis ; Harry’s hourly wage is 1.5 times Mike’s.
B. 8 left parenthesis x plus 1.5 y right parenthesis; Mike’s hourly wage is 1.5 times Harry’s.
C. 12 left parenthesis 8 x plus y right parenthesis ; Harry’s hourly wage is 8 times Mike’s.
D. 8 left parenthesis x plus 4 y right parenthesis ; Mike’s hourly wage is 4 times Harry’s.
Answers
CAN SOMEONE CHECK MY GEOMETRY WORK? 25 POINTS.
Picture attached. If so please tell me what I did wrong thx

Answers
Step 3 is unnecessary (the statement is already given, plus you haven't proven the triangle is isosceles anyway).
After, omit step 5 and jump straight to 6.
After this, step 6 is the statement that used to be step 5, which is true by CPCTC.
Then, you can prove the required statement by definition from this.
Help me please it’s due today

Answers
2. B. 25%
3. C. 35%
I think.
Entered [e^(-t)]*[(66/7)-(10/[7*(t^2))] Answer Preview e^-t(66/7 - 10/7t^2)
Consider the initial value problem (*) {t y" + (2t+8) y' + (t + 8) y=0
{y(1) = 8/e and y'(1) = 2/e Given that y1(t) = e^-t is a solution of the differential equation, solve the initial value problem (*) y(t) = e^(-t)(66/(7)-10/(7t^(2))) Your answer should be a function of t.
Answers
y2(t) = t * e^(-t) is a solution of the homogeneous equation y'' + (2 - 1/t) y' + (1 + 8/t) y = 0. We will use the method of variation of parameters to determine a particular solution to the nonhomogeneous equation y'' + (2t+8) y' + (t+8) y = 0.First, we need to find the Wronskian of y1(t) = e^(-t) and y2(t) = t * e^(-t).W(y1, y2)(t) = | e^(-t) t e^(-t) | = -e^(-t)By the variation of parameters formula, the particular solution is given by y(t) = - y1(t) * integral[(y2(s) f(s)) / (W(y1, y2)(s))] ds + y2(t) * integral[(y1(s) f(s)) / (W(y1, y2)(s))] dswhere f(t) = 0 and W(y1, y2)(t) = -e^(-t).Thus, y(t) = c1 * e^(-t) + c2 * t e^(-t)where c1 and c2 are constants to be determined from the initial conditions.y(1) = c1 * e^(-1) + c2 * e^(-1) = 8/e ---> (1)c1 + c2 = 8y'(1) = - c1 * e^(-1) + c2 * e^(-1) + c2 * e^(-1) = 2/e ---> (2)- c1 + 2c2 = 2/eSolving the system (1)-(2) yields c1 = 10/e and c2 = -2/e.The solution to the initial value problem is thus:y(t) = e^(-t) * (66/7 - 10/(7t^2)).The 100 word answer:Thus, the solution to the given initial value problem is y(t) = e^(-t) * (66/7 - \(10/(7t^2)).\)
A group of 11 students says their favorite animal is the cat. A separate group of 17 students says their favorite animal is the dog. Every student then flips a coin. What are the odds that 7 of the cat-loving students get Heads while 12 of the dog-loving students get Tails?
Answers
The odds that 7 of the cat-loving students get Heads while 12 of the dog-loving students get Tails are approximately 0.004.
The odds that 7 of the cat-loving students get Heads while 12 of the dog-loving students get Tails can be calculated using the binomial probability formula. The probability of a cat-loving student getting a Head is 0.5, and the probability of a dog-loving student getting a Tail is also 0.5. The formula for the binomial probability is P(X = k) = C(n, k) * p^k * (1 - p)^(n - k), where n is the total number of trials, k is the number of successful outcomes, p is the probability of success, and C(n, k) represents the number of ways to choose k successes from n trials.
In this case, we have 11 cat-loving students and 17 dog-loving students. We want to find the probability that exactly 7 cat-loving students get Heads and exactly 12 dog-loving students get Tails. Using the binomial probability formula, we can calculate P(X = 7) as follows:
P(X = 7) = C(11, 7) * (0.5)^7 * (0.5)^(11 - 7) * C(17, 12) * (0.5)^12 * (0.5)^(17 - 12)
To calculate the odds, we divide the probability of the desired outcome by the probability of the complementary outcome (not getting 7 Heads for cat-loving students and 12 Tails for dog-loving students). The odds are given by the formula Odds = P(X = k) / P(X ≠ k).
In this case, the main answer would be the calculated value of P(X = 7) divided by the probability of the complementary outcome.
So, to calculate the exact probability and odds, we can use the binomial coefficient to calculate the number of ways to choose the successful outcomes. The binomial coefficient C(n, k) represents the number of ways to choose k successes from n trials.
For the probability of getting exactly 7 Heads for cat-loving students and 12 Tails for dog-loving students:
P(X = 7) = C(11, 7) * (0.5)^7 * (0.5)^(11 - 7) * C(17, 12) * (0.5)^12 * (0.5)^(17 - 12)
C(11, 7) = 330 (number of ways to choose 7 successes out of 11 trials)
C(17, 12) = 6188 (number of ways to choose 12 successes out of 17 trials)
(0.5)^7 = 0.0078125 (probability of getting 7 Heads for cat-loving students)
(0.5)^12 = 0.000244140625 (probability of getting 12 Tails for dog-loving students)
Now we can calculate P(X = 7):
P(X = 7) = 330 * 0.0078125 * 0.0078125 * 6188 * 0.000244140625 ≈ 0.003983
To calculate the odds, we need to calculate the probability of the complementary outcome (not getting 7 Heads for cat-loving students and 12 Tails for dog-loving students):
P(X ≠ 7) = 1 - P(X = 7) ≈ 1 - 0.003983 = 0.996017
Finally, the odds can be calculated as:
Odds = P(X = 7) / P(X ≠ 7) ≈ 0.003983 / 0.996017 ≈ 0.004
Therefore, the odds that 7 of the cat-loving students get Heads while 12 of the dog-loving students get Tails are approximately 0.004.
Learn more about binomial probability here:
brainly.com/question/12474772
#SPJ11
suppose a = {0,2,4,6,8}, b = {1,3,5,7} and c = {2,8,4}. find: (a) a∪b (b) a∩b (c) a −b
Answers
The result of each operation is given as follows:
a) a U b = {0, 1, 2, 3, 4, 5, 6, 7, 8}.
b) a ∩ b = {}.
c) a - b = {0, 2, 4, 6, 8}.
How to obtain the union and intersection set of the two sets?The union and intersection sets of multiple sets are defined as follows:
The union set is composed by the elements that belong to at least one of the sets.The intersection set is composed by the elements that belong to at all the sets.Item a:
The union set is composed by the elements that belong to at least one of the sets, hence:
a U b = {0, 1, 2, 3, 4, 5, 6, 7, 8}.
Item B:
The two sets are disjoint, that is, there are no elements that belong to both sets, hence the intersection is given by the empty set.
Item c:
The subtraction is all the elements that are on set a but not set b, hence:
a - b = {0, 2, 4, 6, 8}.
More can be learned about union and intersection at brainly.com/question/4699996
#SPJ1
solve quadratic equation x²-8x-1=0 by formula method
Answers
Answer:
x²-8x-1=0
comparing above equation with ax²+bx+c=0
a=1
b=-8
c=-1
x=
\(x = \frac{ - b + - \sqrt{ {b}^{2} - 4ac } }{2a} \)
=(--8+-√(64-4×1×-1)/2×1
=8+-√(64+4)/2
taking positive
x=(8+√68)/2=2(4+√17)/2=4+√17
taking negative
x=(8-√68)/2=2(4-√17)/2=4-√17
solve 15 2x = 36. round to the nearest ten-thousandth.
Answers
To solve the equation 15 + 2x = 36, we can start by subtracting 15 from both sides of the equation to get 2x = 21. Then, we can divide both sides by 2 to get x = 10.5. Rounded to the nearest ten-thousandth, the solution is x = 10.5000.
£240 is divided between Sara, Gordon & Malachy so that Sara gets twice as much as Gordon, and Gordon gets three times as much as Malachy. How much does Gordon get? (Quick Pls)
Answers
Explanation:
Sarah gets twice as much as Gordon and Gordon gets three times as much as Malachy, which means that Malachy gets 1 part of the money, Gordon gets 3 parts because he has three times as much as Malachy, and Sarah gets 6 because she gets twice as much as Gordon. As a ratio from Sarah to Gordon to Malachy its 6:3:1. All of that adds up to £240. If u add 6+3+1 it gives you 10. 240/10 is £24. And Gordon has 3 parts so you do 3x24 which gives you £72
Answer:
£72
Step-by-step explanation:
let Malachy amount be x then Gordon's is 3x and Sara is 2 × 3x = 6x
Then
x + 3x + 6x = 10x = £240 ( divide both sides by 10 )
x = £24
Gordon gets 3x = 3 × £24 = £72
If you had money in a savings account earning 9% interest per year, how much would you make in interest on a deposit of $60.00 over two years?
Answers
The amount of interest earned on a deposit of $60.00 at a rate of 9% per annum for 2 years is $108.
As per the given problem:
Amount deposited = $60.00
Interest rate per year = 9%
The formula for calculating the interest is given by:
Interest = (Principal × Rate × Time)/100
Where Principal is the initial amount invested or deposited
Rate is the percentage of interest that you earn per annum
Time is the duration for which you want to calculate the interest
Putting the values in the above formula, we get:
Interest = (60 × 9 × 2)/100= (108 × 1)/1= $108
So, the amount of interest earned on a deposit of $60.00 at a rate of 9% per annum for 2 years is $108.
for such more question on interest
https://brainly.com/question/25845758
#SPJ11
hte number of left handed people in the world is one-tenth the number of right handed people. the percent of right-handed people
Answers
The percentage of right-handed people is 1%.
What do you mean by the term percent?Percent signifies out of one hundred. It is frequently represented by the symbol "%," even when there aren't 100 entries. After that, the figure is scaled so that it can be put in comparison with 100. Additionally, changes in numerical quantities are denoted by percentages.
We have a bowl of fruit, for instance, with three apples and one orange. Three out of four, or 3/4, or 75 out of 100, or 75 percent, are apples.
A ratio can also be expressed as a fraction or decimal in addition to being written as a percentage. There are methods for converting decimals or fractions to percentages.
To learn more about percent, Visit:
https://brainly.com/question/1787816
#SPJ4
A water trough has a vertical cross section of an equilateral triangle with sides = 6. The trough is 12 feet long. It is being filled at the rate of 4 cubic feet per minute. How fast is the level of water rising at the instant the water reaches a depth of 2 feet? WILL GIVE BRAINLY TO BEST ANSWER + REPORT USELESS ANSWERS
Answers
the level of water is rising at approximately 0.05 feet per minute at the instant the water reaches a depth of 2 feet
Now, First, we need to find the volume of water in the trough when the depth is 2 feet.
Since the cross section is an equilateral triangle, we can use the formula for the area of an equilateral triangle
(A = (√(3)/4) × s) to find the area of the cross section.
Hence,
A = (√(3)/4) × 6
A = 9√(3)
Then, we can use the formula for the volume of a triangular prism
V = A x l) to find the volume of water in the trough.
V = 9√(3) × 12
V = 108√3) cubic feet
Now that we know the volume of water, we can use the formula for the rate of change of volume with respect to time dV/dt = A dh/dt) to find how fast the level of water is rising at the instant the water reaches a depth of 2 feet.
dV/dt = 4 cubic feet per minute
A = 9√(3) h = 2 feet
dV/dt = A dh/dt
4 = 9sqrt(3) dh/dt
dh/dt = 4 / (9sqrt(3))
dh/dt ≈ 0.05 feet per minute
Therefore, the level of water is rising at approximately 0.05 feet per minute at the instant the water reaches a depth of 2 feet
Learn more about the multiplication visit:
https://brainly.com/question/10873737
#SPJ1
The floor of the cage measures 11 yardyard wide by 66 feetfeet long. One bag of shavings covers 55 square feetfeet. How many bags will HarperHarper have to buy to cover the floor of the cage? Explain.
Answers
Answer:
3 3/5 bags
Step-by-step explanation:
We have to find the surface area of the floor of the cage first.
The cage measures 1 yard wide by 6 feet long.
1 yard = 3 feet
The floor of the cage is rectangular, so, the surface area of the floor of the cage is therefore:
3 * 6 = 18 square feet
One bag of shavings covers 5 square feet.
To find the number of bags we need to cover the floor, we divide the surface area of the floor by the number of bags per square feet.
The number of bags needed for the floor of the cage is therefore :
18 / 5 = 3 3/5 bags
The roots of the quadratic function are -2 and -6.Which of the following are the two factors of the quadratic expression?X + 2X-2X - 6X + 6X + 8X - 8
Answers
roots = {-2, -6}
Factors: (x + 6) and (x + 2)
please help ASAP. it is due soon

Answers
Answer:
5 10 15 20
4 8 12 16
Step-by-step explanation:
Flour: 5,10,15,20
Sugar:4,8,12,16
so the amount of flour you need is 20 cups and the amount of sugar is 16 cups
103^2 = (100 + ⋯ )^2 = 100^2 + ⋯ + ⋯
I need help Filling in the blank spaces, Urgent
Answers
Step-by-step explanation:
Notes;(a+b)² = (a+b) × (a+b)
= a(a+b) × b(a+b)
= a² +ab + ba + b²
= a² + b² + 2ab
similarly , (a-b) = a² + b² - 2ab so , The question :-103² = (100 + 3)²
= 100² + 3² + (2×100×3)
= 10000 + 9 + 600
= 10609
Find volume PLS HELP

Answers
Answer:
88.3
I just think so
I dont have a 20 letter explantion
what property of addition is 36+14+29 in
Answers
An article costs Rs 750. all prices are reduced by 40 % in a sale.
find its sale price.
Answers
Answer:
Rs. 450
Step-by-step explanation:
Selling Price ----- 750
Reduced by 40% therefore 40/100 x 750
=300
750-300= 450
Answer:
$450
Step-by-step explanation:
40 percent *750 =
(40:100)*750 =
(40*750):100 =
30000:100 = 300
750-300=$450
x• 7 if x = what is the value of this expression? 4
Answers
Answer:
Step-by-step explanation:
Point Q is plotted on the coordinate grid. Point P is at (30, −30). Point R is vertically above point Q. It is at the same distance from point Q as point P is from point Q. Which of these shows the coordinates of point R and its distance from point Q? (1 point)
On a coordinate grid from negative 50 to positive 50 in increments of 10, Point Q is plotted at the ordered pair negative 40, negative 30.
Group of answer choices
Point R is at (−40, 40), a distance of 70 units from point Q
Point R is at (−40, 20), a distance of 10 units from point Q
Point R is at (−40, −40), a distance of 70 units from point Q
Point R is at (−40, −20), a distance of 10 units from point Q
Answers
Answer:
(a) Point R is at (−40, 40), a distance of 70 units from point Q
Step-by-step explanation:
Point Q is on the same horizontal line as P, but is 30 -(-40) = 70 units away. If point R is 70 units above point Q, its y-coordinate will be -30 +70 = 40.
Point R is at (−40, 40), a distance of 70 units from point Q

