Answers
Answer:
\(\sqrt{17}\)
Related Questions
Express in the form n : 1
Give n as a fully simplified fraction.
6 : 14
Answers
Step-by-step explanation:
simplified fraction is:6/4=3/2 bucose you divide 6 and 4 for 2
Blue points, blue line segments, red points, and red line segments arranged on a Cartesian coordinate plane. Here are the blue points and their coordinates. Point A: (negative nine, 3). Point B: (negative 11, 3). Point C: (negative 10, 3). Point D: (negative 10, 5). Point F: (negative 10, 4). Point E: (negative 11, 4). Here are the red points and their coordinates. Point A-1: (negative 1, 6). Point A-2: (negative 3, 4). Point B-1: (negative 2, 4). Point B-2: (negative 5, 4). Point C-2: (negative 3, 3). Point D-1: (negative 5, 5). Point D-2: (negative 5, 3). Point E-1: (negative 6, 6). Point F-1: (negative 5, 6). A semicircle that lies below its line of symmetry AB. A semicircle that lies above its line of symmetry B-2 A-2. A triangle DEF. A triangle D-1 E-1 F-1. Line segments are drawn from C to D, from A-1 to B-1, from A-2 to B-2, and from C-2 to D-2. Triangle DEF, segment CD, and the semicircle with line of symmetry BA are arranged so that they look like a boat.1.What transformations would you use on the blue triangle to get it to match with the red triangle? Explain your movement using the coordinates of the vertices.

Answers
Transformation blue triangle.
Point D.
coordinates(-10,5)
and the point D1 have coordinates: (-5,5)
The transformation will be over the x-axis:
\(\begin{gathered} D(-10,5) \\ D(-10+5,5)=(-5,5) \end{gathered}\)Point F.
Coordinates(-10,4 ).
Ans the point F1 have coordinates: ( -5,6)
The transformation will be over both axis, x and y:
\(\begin{gathered} F=(-10,4) \\ F(-10+5,\text{ 4+2 })=(-5,\text{ 6}) \end{gathered}\)Point E.
Coordinates: (-11,4)
The point E1 have coordinates: (-6, 6),
The tranformation will be over both axis once again.
\(\begin{gathered} E(-11,\text{ 4}) \\ E(-11+5,\text{ 4+2})=(-6,6) \end{gathered}\)Conclusion: on the x-axis, it shifts 5 points to the right, while on the y-axis it shifts up 2 points only for points E and F.
which system of equations shown below could be used to solve the following problem?
the sum of m and n is 32, and the value of m is three times the value of n. What is the value of n?

Answers
An equation is formed of two equal expressions. The correct option is C.
What is an equation?An equation is formed when two equal expressions are equated together with the help of an equal sign '='.
The given statement in the form of equations can be written as,
1. The sum of m and n is 32 ⇒ m + n = 32
2. The value of m is three times the value of n ⇒ m=3n
Hence, the correct option is C.
Learn more about Equation:
https://brainly.com/question/2263981
#SPJ1
A student weight 400n take 5sec to claimed up of h of 2 calculate the power
Answers
The power required for a student to climb a height of 2 meters in 5 seconds, while weighing 400 Newtons, can be calculated.
Power is defined as the rate at which work is done or energy is transferred. To calculate power, we need to determine the amount of work done and divide it by the time taken. In this case, the work done is equal to the product of force and displacement. The force is the weight of the student, which is 400 Newtons, and the displacement is the height climbed, which is 2 meters. The work done would be 400 Newtons multiplied by 2 meters, resulting in 800 Joules. To calculate power, we divide the work done (800 Joules) by the time taken (5 seconds), which gives us a power of 160 Watts. Therefore, the power required for the student to climb a height of 2 meters in 5 seconds is 160 Watts.
To learn more about power: -brainly.com/question/29575208#SPJ11
What is -2(-x+5y-4) (simplify equation)
Answers
Using the distributed property, the simplified form of -2(-x+5y-4) is 2x-10y+8.
In the equation question,
The given expression is -2(-x+5y-4).
We have to simplify the given expression.
We simplify the given expression using the distributed method.
In the distributed method we have to multiply the number outside the bracket to all the terms that are inside the bracket.
As a(b+c) = ab+bc
In the given question there is -2 outside the bracket and -x+5y-4 is inside the bracket.
To simplify the given expression we multiply -2 to each term inside the bracket.
-2(-x+5y-4) = (-2)×(-x)+(-2)×5y-(-2)×4
Simplifying
-2(-x+5y-4) = 2x+(-10)y-(-8)
Simplifying the bracket
-2(-x+5y-4) = 2x-10y+8
Hence, the simplified form of -2(-x+5y-4) is 2x-10y+8.
To learn more about distributed property link is here
https://brainly.com/question/5637942
#SPJ1
Use the scale to help you solve the equation.
x + 122
334
e

Answers
Answer:
A. x = 212
Step-by-step explanation:
This scale is showing us that x + 122 is equal to 334 because the scale is balanced and we can see an equal sign (=) in the center. We will set up an equation and solve for x.
[Equation]
x + 122 = 334
[Subtract 122 from both sides]
x = 212
A. x = 212
Using the quadratic formula to solve 2x^2 = 4x - 7, what are the values of x?
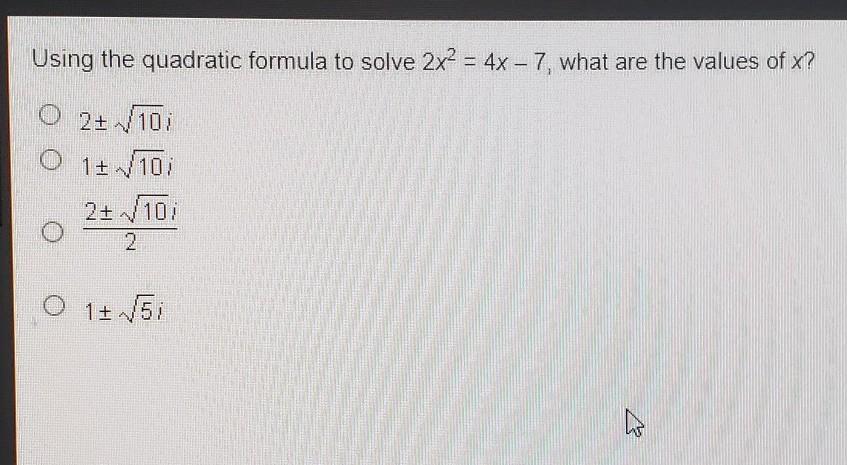
Answers
Answer:
Is C.
Step-by-step explanation:
Consider,
2x² = 4x - 7
2x² - 4x + 7 = 0
using Quadratic Formula
Therefore, Option C is correct.
CAN SOMEONE HELP ME PLEASE I don't know what -2 1/3+(-1 3/4)=? in factions
Answers
The solution to the fraction expression -2 1/3 + (-1 3/4) is -4 1/12
How to evaluate the fraction?The fraction expression is given as
-2 1/3 + (-1 3/4) =
Express the terms of the expression as an improper fraction
So, we have
-2 1/3 + (-1 3/4) = -7/3 + (-7/4)
Remove the bracket in the above expression.
So, we have
-2 1/3 + (-1 3/4) = -7/3 - 7/4
Take the LCM in the above expression.
So, we have
-2 1/3 + (-1 3/4) = (-7 * 4 - 7 * 3)/12
Evaluate the difference
-2 1/3 + (-1 3/4) = -49/12
Express the fraction as a mixed fraction
-2 1/3 + (-1 3/4) = -4 1/12
Hence, the solution to the fraction expression -2 1/3 + (-1 3/4) is -4 1/12
Read more about fractions at
https://brainly.com/question/11562149
#SPJ1
use the power series 1 1 x = [infinity] (−1)nxn n = 0 , |x| < 1 to find a power series for the function, centered at 0. h(x) = −2 x2 − 1 = 1 1 x 1 1 − x
Answers
This power series is centered at 0 and represents the function h(x) = −2x^2 − 1.
To find the power series for h(x) = −2x^2 − 1, we can start with the power series expansion for 1/(1 − x), which is given by ∑ (-1)^n * x^n for |x| < 1. We want to manipulate this series to obtain the desired function h(x).
First, we multiply the power series by x^2 to obtain ∑ (-1)^n * x^(n+2). This shifts the powers of x by 2, resulting in x^2, x^3, x^4, and so on.
Next, we multiply the entire series by 2 to obtain ∑ (-1)^n * 2x^(n+2). This scales the coefficients by a factor of 2.
Finally, we subtract 1 from the series to obtain ∑ (-1)^n * 2x^(n+2) - 1. This subtracts 1 from each term of the series.
Therefore, the power series representation of h(x) is ∑ (-1)^n * 2x^(n+2) - 1. This power series is centered at 0 and represents the function h(x) = −2x^2 − 1.
Learn more about power series here:
https://brainly.com/question/29896893
#SPJ11
what are the first six digits of the mathematical sign pi?
Answers
The first six digits of the mathematical sign PI are 3.14159.
Pi is a mathematical constant that is commonly used in geometry and trigonometry. The number is defined as the ratio of a circle's circumference to its diameter, and it is approximately 3.14159.
The value of PI has been computed to millions of decimal places, but the first six digits, which are 3.14159, are the most often used in computations.
The first six digits of the mathematical sign PI are 3.14159. These digits are frequently used to calculate the value of a circle's circumference or area. Pi is irrational, which means it can't be expressed as a fraction of two integers, and it goes on indefinitely without repeating.
Learn more about pi : https://brainly.com/question/31248489
#SPJ11
Find the value of the expression. Enter your answer in the box. `2+(6+1)^2-8
Answers
The value of the expression as given in the task content is; 43.
What is the value of the expression given in the task content?The value of the expression given in the task content can be determined by means of the PEMDAS rule as follows;
2 +(6+1)² -8
= 2 +7² -8
= 2 + 49 -8
= 43.
Read more on PEMDAS;
https://brainly.com/question/1094951
#SPJ4
The population of a city has decreased by 26% since it was last measured. If the current population is 40,700, what was the previous population?
Answers
The previous population, of the city is 55,000
What is percentage?A percentage is a number or ratio that can be expressed as a fraction of 100. If we have to calculate percent of a number, divide the number by the whole and multiply by 100.
Given that, a city's current population is 40,700, decreased by 26% after it was measured last time, the
Let the previous population, of the city, be x,
Therefore,
x - 26% of x = 40,700
x(1-26%) = 40,700
0.74x = 40,700
x = 55,000
Hence, the previous population, of the city is 55,000
Learn more about percentage, click;
https://brainly.com/question/1578304
#SPJ9
a department store is having a sale on jackets. originally the jackets were selling for $90. after the discount, the jackets cost $60. what is the percent of the discount
Answers
The percent discount on the jackets is 33.33%. To find the percent of the discount, we need to calculate the difference between the original price and the discounted price, and then express it as a percentage of the original price.
The difference between the original price and the discounted price is $90 - $60 = $30.
To express this as a percentage of the original price, we can use the formula:
percent discount = (discount / original price) x 100
Plugging in the values we get:
percent discount = ($30 / $90) x 100 = 33.33%
Therefore, the percent discount on the jackets is 33.33%.
Learn more about percent discount
https://brainly.com/question/24261067
#SPJ4
Dialation by a factor of 5/6
Answers
Answer:
i dnt know what you are asking for but if it is area it will be the area times 5/6
Step-by-step explanation:
A submarine descends 45 meters on its first dive. It then descends another 40 meters. What integer represents the total descent in meters for the two dives?
Answers
Answer:
85 meters in total
Step-by-step explanation:
The submarine first descended 45 meters and then 40 meters
45+40=85
PART 1 Please help me 10 points i just joined today ;)
PART 2 is on other question





Answers
Answer:
B=30,000
Y=The Plane's altitude
M= -2,000
X= Minutes
Equation: y=-2,000x+30,000
Slope= ?
Y-intercept= the point where you start at
what is the altitude after 10 minutes?=10,000
How Long does it take to get to 0 altitudes?=15 (Minutes)
Step-by-step explanation:
What are the choices for slope
Write an equation of the line below.

Answers
Answer: y = -2/5x + 3
Step-by-step explanation:
The formula for a line is: y = mx + b.
m is the slope of the line. We calculate this by looking at how many units the line travels vertically over how many units the line travels horizontally, or rise over run. In this example, we can see that the line goes down 2 units for every 5 it goes to the right, meaning the slope is equal to -2/5.
b is the y-intercept, or where the line crosses the y-axis. In this example, the line crosses the y-axis at (0, 3) making the b value equal to 3.
Therefore, the equation for this line put together is y = -2/5x + 3.
If a=0.05, how would you interpret the following p value for a hypothesis test to evaluate the difference between two groups? 0.01 < p < 0.05 Accept the alternative hypothesis and conclude that there is not a statistically significant difference between groups. Reject the null hypothesis and conclude that there is a statistically significant difference between groups. Reject the null hypothesis and conclude that there is not a statistically significant difference between groups. None of these Fail to reject the null hypothesis and conclude that there is a statistically significant difference between groups. Fail to reject the null hypothesis and conclude that there is not a statistically significant difference between groups.
Answers
Based on the given p-value of 0.01 < p < 0.05 and assuming a significance level of a=0.05, we would fail to reject the null hypothesis and conclude that there is not a statistically significant difference between the two groups being compared.
This means that the observed difference between the two groups may be due to chance and not a true difference in the populations being studied.
If a=0.05, a p-value less than or equal to 0.05 would indicate statistical significance, meaning that we would reject the null hypothesis and conclude that there is a statistically significant difference between the two groups.
However, in this case, the p-value is given as 0.01 < p < 0.05, which means that the p-value is greater than 0.01 but less than 0.05. This indicates that the difference between the two groups may not be statistically significant at the 0.01 level, but it may still be statistically significant at the 0.05 level.
To learn more about significance level, refer:-
https://brainly.com/question/13947717
#SPJ11
find the volume of the given solid. bounded by the coordinate planes and the plane 6x + 4y + z = 24
Answers
Therefore, the volume of the solid bounded by the coordinate planes and the plane 6x + 4y + z = 24 is 96 cubic units.
To find the volume of the solid bounded by the coordinate planes (xy-plane, xz-plane, and yz-plane) and the plane 6x + 4y + z = 24, we need to determine the region in space enclosed by these boundaries.
First, let's consider the plane equation 6x + 4y + z = 24. To find the x-intercept, we set y = 0 and z = 0:
6x + 4(0) + 0 = 24
6x = 24
x = 4
So, the plane intersects the x-axis at (4, 0, 0).
Similarly, to find the y-intercept, we set x = 0 and z = 0:
6(0) + 4y + 0 = 24
4y = 24
y = 6
So, the plane intersects the y-axis at (0, 6, 0).
To find the z-intercept, we set x = 0 and y = 0:
6(0) + 4(0) + z = 24
z = 24
So, the plane intersects the z-axis at (0, 0, 24).
We can visualize that the solid bounded by the coordinate planes and the plane 6x + 4y + z = 24 is a tetrahedron with vertices at (4, 0, 0), (0, 6, 0), (0, 0, 24), and the origin (0, 0, 0).
To find the volume of this tetrahedron, we can use the formula:
Volume = (1/3) * base area * height
The base of the tetrahedron is a right triangle with sides of length 4 and 6. The area of this triangle is (1/2) * base * height = (1/2) * 4 * 6 = 12.
The height of the tetrahedron is the z-coordinate of the vertex (0, 0, 24), which is 24.
Plugging these values into the volume formula:
Volume = (1/3) * 12 * 24
= 96 cubic units
To know more about volume of the solid,
https://brainly.com/question/30079268
#SPJ11
What is the solution to the equation square root 2x + 6 - square root x + 4 = 1
Answers
raAnswer:
x = 5
Step-by-step explanation:
Original equation = \(\sqrt{2x+6}\) - \(\sqrt{x+4}\) = 1
Remove square roots
\(x^{2}\) + 2x +1 = 4x +16
Subtract 16 from both sides
\(x^{2}\)+ 2x +1 = 4x +16
-16 -16
---------------------------
\(x^{2}\) + 2x- 15= 4x
Subtract 4x from both sides
\(x^{2}\) + 2x - 15 - 4x= 4x - 4x
= \(x^{2}\) - 2x - 15 = 0
THIS EQUATION HAS 2 rational roots. {x1,x2} = {5,-3}
CHECK THAT THE FIRST SOLUTION IS CORRECT (5)
Original equation, root isolated, after tidy up
\(\sqrt{2x+6}\) = \(\sqrt{x+4}\)
Plug in 5 for x
\(\sqrt{2\cdot (5)+6}\) = \(\sqrt{(5)+4+1}\)
Simplify
\(\sqrt16}\) = 4
Solution checks !!
Solution is: x = 5
CHECK THAT THE SECOND SOLUTION IS CORRECT (-3)
Original equation, root isolated, after tidy up
\(\sqrt{2x+6}\) = \(\sqrt{x+4}\)
Plug in -3 for x
\(\sqrt{2\cdot (-3) +6}\) = \(\sqrt{(-3)+4+1}\)
Simplify
\(\sqrt{0}\) = 2
Solution does not check
0 ≠ 2
So, the answer is x = 5
Hope this helps!
Which number, when rounded to the nearest tenth, is 43.6?
Answers
Answer:44
Step-by-step explanation:
Answer:
Is this multiple choice?
Step-by-step explanation:
Between 43.55 and 43.649
If 0.50 mol of Na3PO4 is mixed with 0.30 mol of Bacl2, the maximum number of moles o barium phosphate which can be formed is? A. 0.10 B. 0.15 C. 0.30 D. 0.50
Answers
The maximum number of moles of barium phosphate that can be formed is B) 0.15 mol, which corresponds to the amount of BaCl2 present. Therefore, the answer is (B) 0.15.
The balanced chemical equation for the reaction between sodium phosphate (Na3PO4) and barium chloride (BaCl2) is:
3 Na3PO4 + 2 BaCl2 → Ba3(PO4)2 + 6 NaCl
From the balanced equation, we can see that 2 moles of BaCl2 react with 3 moles of Na3PO4 to form 1 mole of Ba3(PO4)2.
Therefore, the limiting reactant in this reaction is the one that will be completely consumed first. To determine the limiting reactant, we need to compare the number of moles of each reactant with the stoichiometric ratio in the balanced equation.
For Na3PO4:
3 moles Na3PO4 = 1 mole Ba3(PO4)2
0.50 mol Na3PO4 = (1/3) × 0.50 mol Ba3(PO4)2 = 0.167 mol Ba3(PO4)2
For BaCl2:
2 moles BaCl2 = 1 mole Ba3(PO4)2
0.30 mol BaCl2 = (1/2) × 0.30 mol Ba3(PO4)2 = 0.15 mol Ba3(PO4)2
Therefore, the maximum number of moles of barium phosphate that can be formed is 0.15 mol, which corresponds to the amount of BaCl2 present.
for such more question on barium phosphate
https://brainly.com/question/14929403
#SPJ11
a random sample x1,x2 ...,xn of size n is taken from a poisson distribution with a mean of λ, 0 < λ < [infinity]. (a) show that the maximum likelihood estimator for λ is bλ
Answers
To find the maximum likelihood estimator (MLE) for λ, we need to maximize the likelihood function L(λ) with respect to λ of the Poisson distribution
First, let's write the probability density function (PDF) of the Poisson distribution:
P(X = k) = (e^(-λ) * λ^k) / k!
The likelihood function can be defined as the product of the probabilities for each observation in the random sample. Since the sample is independent and identically distributed, we can write the likelihood function as:
L(λ) = P(x1, x2, ..., xn | λ) = P(x1 | λ) * P(x2 | λ) * ... * P(xn | λ)
Taking the logarithm of the likelihood function (log-likelihood) will simplify the calculations. The log-likelihood function is:
log(L(λ)) = log(P(x1 | λ)) + log(P(x2 | λ)) + ... + log(P(xn | λ))
Now, let's calculate the derivative of the log-likelihood function with respect to λ:
d/dλ log(L(λ)) = d/dλ (log(P(x1 | λ)) + log(P(x2 | λ)) + ... + log(P(xn | λ)))
= d/dλ (log(P(x1 | λ))) + d/dλ (log(P(x2 | λ))) + ... + d/dλ (log(P(xn | λ)))
To find the MLE, we set the derivative equal to zero and solve for λ:
d/dλ log(L(λ)) = 0
The derivative of log(P(x | λ)) with respect to λ can be calculated using the logarithmic differentiation technique. After taking the derivative, we equate it to zero and solve for λ.
By solving the equation, we will obtain the MLE for λ.
Learn more about Poisson distribution: https://brainly.com/question/9123296
#SPJ11
the diagonal of a cube is 2020 cmcm. identify the length of an edge. round to the nearest tenth, if necessary.
Answers
The length of an edge of the cube is approximately 1428.7 cm when rounded to the nearest tenth.
To find the length of an edge, we can use the relationship between the diagonal and the edge length of a cube. In a cube, the diagonal is the hypotenuse of a right triangle formed by three edges. Let's assume the length of an edge is "x."
According to the Pythagorean theorem, the square of the diagonal is equal to the sum of the squares of the three edges:
\(diagonal^2 = x^2 + x^2 + x^2\)
Simplifying the equation:
\(2020^2 = 3x^2\)
Solving for "x," we can take the square root of both sides:
\(x = \sqrt{(2020^2 / 3)} = 1428.7 cm\)
Therefore, the length of an edge of the cube is approximately 1428.7 cm when rounded to the nearest tenth.
In conclusion, the length of the edge of the cube is approximately 1428.7 cm.
To learn more about Pythagorean theorem, visit:
https://brainly.com/question/343682
#SPJ11
need help explain and answer

Answers
The length of points IJ given the total length of HJ and length HI is 8
What is the length of points IJ?The line HJ is measured as 20
If HI = 12
Then, subtract to find IJ
IJ = HJ - HI
= 20 - 12
IJ = 8
Therefore, length of points IJ is 8
Read more on length:
https://brainly.com/question/24487155
#SPJ1
A pile of tailings from a gold dredge is in the shape of a cone. the diameter of the base is 34 feet and the height is 16 feet. approximately, how many cubic feet of gravel is in the pile? use π = 3.14.
Answers
The volume of the cone is 4840 cubic ft if the diameter of the base is 34 feet and the height is 16 feet.
What is a cone?It is defined as a three-dimensional shape in which the base is a circular shape and the diameter of the circle decreases as we move from the circular base to the vertex.
V = πr²h/3
Volume can be defined as a three-dimensional space enclosed by an object or thing.
It is given that:
A pile of tailings from a gold dredge is in the shape of a cone.
The diameter of the base is 34 feet and the height is 16 feet.
As we know,
The volume of the cone is given by:
V = πr²h/3
r = 34/2 = 17 ft
h = 16 feet
Plug the above values in the formula:
v = 1/3 × (3.14 × 17 × 17 × 16 )
V = 1541.33(3.14) cubic feet
V = 4839.78 ≈ 4840 cubic ft
Thus, the volume of the cone is 4840 cubic ft if the diameter of the base is 34 feet and the height is 16 feet
To learn more about the volume of cone from given link
https://brainly.com/question/13007427
#SPJ4
You can use formula A=1/2absin C to find the area of a triangle. What is bsin C equivalent to in the diagram below.
Answers
Let's first understand the formula A=1/2absin C. This formula is used to find the area of a triangle where 'a' and 'b' are the lengths of two sides of the triangle and 'C' is the angle between those sides. The sin C represents the sine of angle C, which is used to calculate the area of the triangle.
Now, coming to the question of what bsin C is equivalent to in the given diagram. Looking at the diagram, we can see that 'b' is one of the sides of the triangle, and 'C' is the angle opposite to 'b'. Using the definition of sin C, we know that sin C is equal to the length of the side opposite to angle C (in this case, 'a') divided by the length of the hypotenuse (in this case, 'c'). So, sin C = a/c.
Multiplying both sides of the equation by 'b', we get:
b sin C = b (a/c)
Here, we can see that 'b sin C' is equivalent to the length of the side adjacent to angle C (in this case, 'b') multiplied by the length of the opposite side (in this case, 'a') divided by the length of the hypotenuse (in this case, 'c'). Therefore, we can conclude that in the given diagram, 'bsin C' is equivalent to 'ab/c'.
To know more about area of a triangle visit -
brainly.com/question/29106474
#SPJ11
If A+B+C=180 and sin a= sin b sin c prove that cot a= 1- cot b cot c
Please help me with this question I'll mark you as brainliest..pleasee with clear explanation and process
Answers
Note that the proof that cot a= 1- cot b cot c is given as follows;
A math proof is a logical argument that uses mathematical reasoning and evidence to support a mathematical statement or theorem.
From the given information, we know that:
A + B + C = 180 ... (1)
sin A = sin B sin C ... (2)
We need to prove that:
cot A = 1 - cot B cot C
We can start by using the identity:
cot x = 1/tan x
So, we can rewrite the above equation as:
1/tan A = 1 - (1/tan B) (1/tan C)
Multiplying both sides by tan A, we get:
1 = tan A - (tan B)(tan C)/(tan A)
Using the identity:
tan (x+y) = (tan x + tan y)/(1 - tan x tan y)
We can write:
tan (A + B + C) = tan 180
Since tan 180 is undefined, we know that:
tan (A + B + C) = tan 0
So, we get:
tan A + tan B + tan C - tan A tan B tan C = 0
Since A + B + C = 180, we can rewrite the above equation using (1) and (2) as:
sin A/cos A + sin B/cos B + sin C/cos C - sin B sin C/sin A = 0
Multiplying both sides by cos A cos B cos C, we get:
sin B cos C cos A + sin C cos A cos B + sin A cos B cos C - sin B sin C cos A = 0
Rearranging, we get:
sin A cos B cos C = sin B cos A cos C + sin C cos A cos B - sin B sin C cos A
Dividing both sides by sin A cos B cos C, we get:
1 = cot A - cot B cot C + cot A cot B cot C
Simplifying, we get:
cot A = 1 - cot B cot C
Hence, the proof is complete.
Learn more about Proof:
https://brainly.com/question/28613847
#SPJ1
i'll pick you as brainily please quick formula for finding the distance between two points
Answers
\(Let \: the \: two \: points \: be \: \underline{\underline{A( x_{1} ,y_{1})}} \: and \: \underline{\underline{B \: ( x_{2}, y_{2})}}\)
Then ,
\(\boxed{d(AB) = \sqrt{ {( x_{2} - x_{1}) }^{2} + {( y_{2} - y_{1}) }^{2} } }\\ \)
where , d(AB) is the distance between the two points A and B.
hope helpful! :)
Answer:
the Distance Between the two points a and b
Step-by-step explanation:
Distance between two points is the length of the line segment that connects the two points in a plane. The formula to find the distance between the two points is usually given by d=√((x2 – x1)² + (y2 – y1)²). This formula is used to find the distance between any two points on a coordinate plane or x-y plane.
What are the solutions for f(x)g(x)

Answers
Answer:
x = -1, 1
Step-by-step explanation:
The solutions to f(x) = g(x) are the x-values where the two functions have the same value.
The functions are both 1 when x = -1.
The functions are both -7 when x = 1.
The two solutions are x = -1, x = 1.

