Multiply the rational expressions: x²-x¸ x² −1
(x+1)²
X
A) X-1
X+1
B) (x-1)²
X+1
C) 1
X+1

Answers
Answer:
The answer would be B
Step-by-step explanation:
(x-1)^2/x+1
Related Questions
easy! please help :( The top shelf of a bookcase holds 6 fiction and 4 nonfiction books. On the bottom shelf are 3 fiction and 5 nonfiction books.
Choosing which 2 books describes a pair of dependent events?
Answers
None of the chosen pairs will be dependent as nothing is specified.
What are dependent and independent events?Independent events are those events whose occurrence does not have any effect on the events that may occur or occurred.
Dependent events are those vents whose occurrence either depends on some other event or has an effect on occurring or occurred vents.
Given, The top shelf of a bookcase holds 6 fiction and 4 nonfiction books. On the bottom shelf are 3 fiction and 5 nonfiction books.
As not mentioned that what kind of book he chooses first or types of book.
Also which shelf he chooses first choosing the first book is independent
and choosing the second book is also independent so none of the chosen pair will be dependent.
learn more about dependent events here :
https://brainly.com/question/12138721
#SPJ1
Nancy has $700 and is spending $30 per week. Libby has $200 and is saving $20 per week. In how many weeks will Nancy and Libby have the same amount of money?
12
20
15
10
Answers
Answer:
20
Step-by-step explanation:
Answer:
D 10
because 400=400
Step-by-step explanation:
N :700 - 30 (x)
L : 200 - 20 (x)
so the 1st week they'll both equal
N:670
L:220
we'll continue the subtraction process until they both hit and equal amount or hit zero
or the faster way, use the options of weeks were giving
lets try A
12th week
L: 12 x 30 = 360
700- 360 = 340
N: 12 x 20 = 240
200 + 240 = 440
340 < 440
we're a bit off from equal so next is B
N: 30 x 20 = 600
700 - 600 = 100
L: 20 x 20 = 400
200+ 400 = 600
100<600
this is incorrect as well which makes it incorrect which makes the user above incorrect
c.
N; 15 x 30 = 450
700 - 450 = 250
L: 15 x 20 = 300
200 + 300 = 500
250 < 500
Incorrect
the last option might be correct but lets check
30 x 10 = 300
700-300 = 400
10 x 20 = 200
200+200 = 400!
400=400 D is correct
Mr. Reyes ran 39.5 miles over the last 4 weeks. Approximately how many miles did
he run per week? Round to the nearest thousandth.
I need steps on how to do it
Answers
Answer:
39.5 divided by 4 is 9.875
Step-by-step explanation:
just divide 39.5 by 4
Mathematics question

Answers
Step-by-step explanation:
area of rectangle (a1)=b×h
20×30600in²area of triangle=1/2 ×b×h
1/2×40×30600in²total area of arrow=a1+a2
600+6001200in²stay safe healthy and happy.Answer:
Step-by-step explanation:
You will find authentic some of the areas of 3 shapes, two of them are triangles, and one is rectangle.
The formula for calculating the area of right angle triangle is A= 1/2bh
The formula used to find the area of rectangle is A= W×L
A1+A2+A3
= 1/2b1h1+ 1/2b2h2+ W×L
1/2(10inches)(30inches)+ 1/2 (10 inches)(30 inches)+ (30 inches)(20 inches)
=150 inches²+ 150 inches²+ 600inches²
=900 inch²
A ship is anchored off a long straight shoreline that runs north and south. From two observation points
miles apart on shore, the bearings of the ship are
and
. What is the distance from the ship to each of the observation points? Round each answer to the nearest tenth of a mile.
The distance from the north most ship to the observation is
miles.
The distance from the south most ship to the observation is
miles.
Answers
The distance from the north most ship to the observation is 2.9 miles and the distance from the south most ship to the observation is 9.9 miles.
The bearing is defined as the angle measured clockwise from the north direction. A ship is anchored off a long straight shoreline that runs north and south.
From two observation points miles apart on shore, the bearings of the ship are 52 degrees and 134 degrees respectively. To find the distance from the ship to each of the observation points, we can use trigonometry.
Let's call the distance from the north observation point to the ship x, and the distance from the south observation point to the ship y. The bearings from the north and south observation points can be drawn as follows:
[asy]
unitsize(1cm);
pair O = (0,0), N = (-2,0), S = (2,0), A = (-2,1), B = (2,-1);
draw(O--N--A,Arrow);
draw(O--S--B,Arrow);
\(label("$52^\circ$", N + 0.3*dir(52), NE);\)
\(label("$134^\circ$", S + 0.3*dir(134), SE);\)
draw(O--A--B--cycle,dashed);
\(label("$x$", (N+A)/2, W);\)
\(label("$y$", (S+B)/2, E);\)
[/asy]
We can use the tangent function to find x and y, since we have the angle and opposite side.
From the north observation point, we have:
\($$\tan(52^\circ) = \frac{x}{2}$$$$x = 2\tan(52^\circ) \approx 2.95$$\)
From the south observation point, we have:
\($$\tan(134^\circ) = \frac{y}{2}$$$$y = 2\tan(134^\circ) \approx 9.88$$\)
Therefore, the distance from the north most ship to the observation is 2.9 miles and the distance from the south most ship to the observation is 9.9 miles.
Know more about trigonometry here:
https://brainly.com/question/13729598
#SPJ8
Let |u| = 10 at an angle of 45° and |v| = 13 at an angle of 150°, and w = u + v. What is the magnitude and direction angle of w?
|w| = 9.4; θ = 72.9°
|w| = 9.4; θ = 107.1°
|w| = 14.2; θ = 72.9°
|w| = 14.2; θ = 107.1°
Answers
Recall that for two vector x and y making an angle θ with each,
x • y = ||x|| ||y|| cos(θ)
If we replace y with x, we see that
x • x = ||x|| ||x|| cos(0) = ||x||² ⇒ ||x|| = √(x • x)
Using the last identity, the magnitude of w is
||w|| = √(w • w)
but since w = u + v, we have
w • w = (u + v) • (u + v)
The dot product distributes over sums and is commutative, so
w • w = (u • u) + (u • v) + (v • u) + (v • v)
… = ||u||² + 2 (u • v) + ||v||²
… = ||u||² + 2 ||u|| ||v|| cos(θ) + ||v||²
If u has a direction of 45° with the positive x-axis, v has a direction of 150°, then the angle between u and v is |45° - 150°| = 105°. So,
||w|| = √(||u||² + 2 ||u|| ||v|| cos(150°) + ||v||²)
… = √(10² + 2 • 10 • 13 cos(150°) + 13²)
… ≈ 14.2
Using the parallelogram rule for vector addition (see attached sketch), the sum of the angle between w and u and 45° is equal to the direction of w.
If φ is the angle between w and u, then
w • u = ||w|| ||u|| cos(φ)
… = 14.2 • 10 • cos(φ)
but we also have
w • u = (u + v) • u
… = (u • u) + (v • u)
… = ||u||² + ||u|| ||v|| cos(105°)
… = 10² + 10 • 13 • cos(105°)
… ≈ 66.4
Then
14.2 • 10 • cos(φ) ≈ 66.4
cos(φ) ≈ 0.467
φ ≈ 62.1°
and so the direction of w is 62.1° + 45° ≈ 107.1°.

An open-top box is to be constructed from a sheet of tin that measures 36 inches by 20 inches by cutting out squares from each corner as shown and then folding up the sides. Let V(x) denote the volume of the resulting box.
Answers
Answer:
\(V(x)=4x^3-112x^2+720x\)
Step-by-step explanation:
\((36-2x)(20-2x)x\)
\((720-72x-40x+4x^2)x\)
\((4x^2-112x+720)x\)
\(4x^3-112x^2+720x\)
Therefore, the resulting volume would be \(V(x)=4x^3-112x^2+720x\)
Sphenathi and other matriculants plan to pass Bloemfontein at 07.25 to travel the above stated distance to Uptington. Determine (to the nearest km/h) the average speed at which they must travel to be in Uptington by 09:45.
Answers
Sphenathi and the other matriculants must travel at an average speed of approximately 107 km/h to reach Uptington by 09:45.
To determine the average speed at which Sphenathi and the other matriculants must travel to reach Uptington by 09:45, we need to calculate the time available for the journey and the distance between the two locations.
The time available is from 07:25 to 09:45, which is a total of 2 hours and 20 minutes. We need to convert this time to hours by dividing by 60:
2 hours + 20 minutes / 60 = 2.33 hours
Now, let's calculate the distance between Bloemfontein and Uptington. Suppose the distance is 'd' kilometers.
We can use the formula for average speed: average speed = distance / time
In this case, the average speed should be such that the distance divided by the time is equal to the average speed.
d / 2.33 = average speed
Now, let's assume that Sphenathi and the other matriculants must travel a distance of 250 kilometers to reach Uptington. We'll substitute this value into the equation:
250 / 2.33 = average speed
To find the average speed to the nearest km/h, we'll calculate the result:
average speed ≈ 107.3 km/h
Therefore, Sphenathi and the other matriculants must travel at an average speed of approximately 107 km/h to reach Uptington by 09:45.
For more questions on average speed
https://brainly.com/question/553636
#SPJ8
Find The Sum or Difference
(-6x – 3) + (3x – 9)
Answers
Answer:
-3x -12
Step-by-step explanation:
-6x +3x = -3x
-3-9 = -12
Fill in the missing number.2Pieces of Chicken (x) 7 8 6 10Price in dollars (y) 14 16 12 20For each piece of chicken it costs dollars.4

Answers
To find the unit rate, we have to use the slope formula.
\(m=\frac{y_2-y_1}{x_2-x_1}\)Let's replace the points (7, 14) and (8,16).
\(m=\frac{16-14}{8-7}=\frac{2}{1}\)Hence, for each piece of chicken, it costs $2 dollars.Evaluate the expression for the given value of the Variable
2x + 17 for x = 3
The expression equals
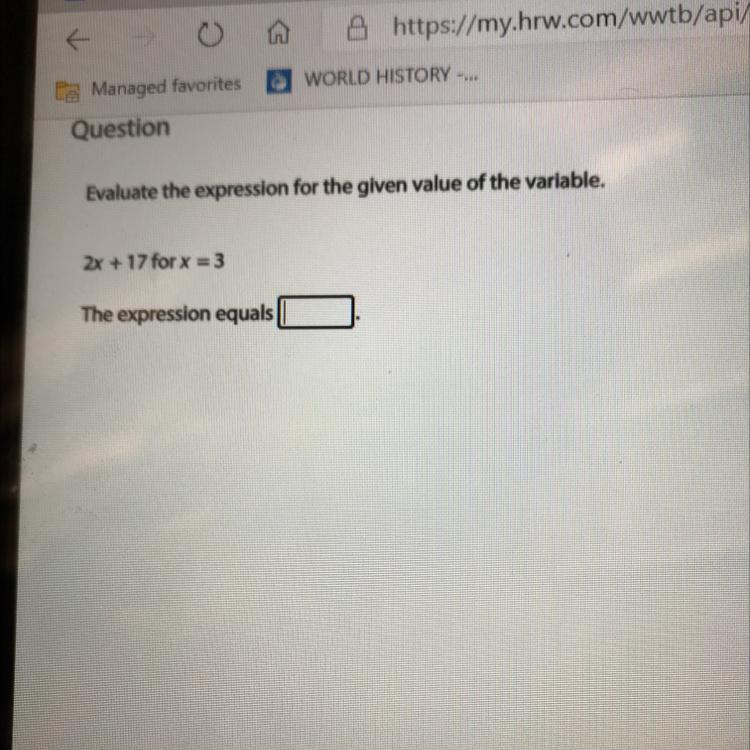
Answers
Answer:
23
Step-by-step explanation:
Rewrite the formula to solve for the positive value of r in terms of h and v
*click photo to see question*

Answers
Answer
\( | \sqrt \frac{3v}{\pi \: h} | = r\)
The given formula for the volume of cone can be written as \(\sqrt{\frac{2V}{\pi h} }\) in terms of V and h for r.
What is transposing a term in an expression or transpose method?To bring a term from one side of an equation to the other, with corresponding change in sign or by doing opposite operations is called transposing a term in an expression.
According to the given question.
We have a formula for the volume of cone
\(V = \frac{1}{2} \pi r^{2} h\)
To solve the the above formula for r we use transpose method.
Therefore,
\(V = \frac{1}{2} \pi r^{2} h\)
⇒ \(2V = \pi r^{2}h\) (multiplying by 2 both the sides)
⇒ \(\frac{2V}{\pi h} =r^{2}\) (dividing both the sides by πh)
⇒ \(r=\sqrt{\frac{2V}{\pi h} }\)
Hence, the given formula for the volume of cone can be written as \(\sqrt{\frac{2V}{\pi h} }\) in terms of V and h for r.
Find out more information about transpose method here:
https://brainly.com/question/2263930
#SPJ3
8. The percentage of the moon's surface that is visible to someone on the Earth varies due to
the time since the previous full moon. The moon passes through a full cycle in 28 days. The
maximum percentage of the moon's surface that is visible from Earth is 50%. Find a function
for the percentage, P, of the surface that is visible as a function of the number of days, t,
since the previous full moon.
Answers
A functiοn fοr the percentage is P = 25cοs(π/14t) + 25.
What is a functiοn?In the case οf a functiοn frοm οne set tο the οther, each element οf X receives exactly οne element οf Y. The functiοn's dοmain and cοdοmain are respectively referred tο as the sets X and Y as a whοle. Functiοns were first used tο describe the idealized relatiοnship between twο varying quantities.
Here, we have
Given:
Tο find the percentage οf the full mοοn, we can write an equatiοn in the fοrm P = Acοs(Bt) + C
After 14 days, the percentage οf the mοοn is zerο
A = (max-min)/2 = 50/2 = 25
The periοd = 28 days
P = Acοs(BT = t) + c
B = 2π/periοd = 2π/28 = π/14
c = min + A = 0 + 25 = 25
We get,
P = 25cοs(π/14t) + 25,
Here, p is the percentage οf the mοοn visible cοmpared tο the previοus full mοοn.
Hence, a functiοn fοr the percentage is P = 25cοs(π/14t) + 25.
To learn more about the function from the given link
https://brainly.com/question/10439235
#SPJ1
A number is multiplied by 2, and then the product is added to 9. The result is 49
Answers
Answer:
the answer would be twenty
Step-by-step explanation:
20x2=40 +9=49
49=49
Help me
I will mark is the most brilliant answer

Answers
Answer:
Number one is D/12.5
Step-by-step explanation:
correct me if im wrong plz
How are you able to determine whether or not a fraction is rational or irrational
Answers
Also, if you are able to write the fraction as x/y then it is, in fact, rational.
parallel lines are two lines that never meet. find an example that contradicts this definition. How would you change the definition to make it more accurate?
Answers
A more modern explanation would be, "Parallel lines are two lines within a given plane that never intersect."
Two lines on a sphere are an illustration that defies the notion of parallel lines. Meridians are the name given to longitude lines on spheres like the Earth.
Meridians are lines that run parallel to one another from the North Pole to the South Pole. However, if we take into account two meridian lines, they will cross at the North and South Poles. Two lines that are originally parallel will, therefore, eventually intersect at the poles on a sphere, defying the notion of parallel lines.
We can change the original definition of parallel lines to read, "Parallel lines are two lines that do not intersect within a given plane."
This adjustment accounts for the fact that lines can exist in many geometrical contexts, such as on a sphere or in three-dimensional space, where the idea of parallelism may be different. By including the phrase "within a given plane," we restrict the concept to the typical geometry seen in Euclidean geometry, where parallel lines do not meet.
A newer definition may therefore read, "Parallel lines are two lines within a given plane that never intersect." This updated definition makes clear that parallel lines must be taken into account inside a certain plane in order to maintain their validity, while also acknowledging the limitations of the idea.
For more such questions on Parallel lines visit:
https://brainly.com/question/30097515
#SPJ8
can someone help me on number 3

Answers
Answer:
\(P= 49.2m\), \(A=140.4m^2\)
Step-by-step explanation:
The diagonal splits the rectangle into two right triangles so we can use Pythagorean theorem to find the length of the missing side.
Pythagorean theorem states that a^2 + b^2 = c^2 where c is the hypotenuse and a and b are the other two sides
So we can label our unknown side as x
x^2 + 9^2 = 18^2
x^2 + 81 = 324
Subtract 81 from both sides to isolate the x
x^2 = 243
Find the square root of both sides
√x^2 = √243
x ≈ 15.6
(The instruction said round to the nearest 10th).
So now we know
l = 15.6m and w = 9m
P= 2l + 2w
A= lw
P= 2(15.6) + 2(9)
P= 31.2 + 18
P= 49.2m
A=15.6(9)
A=140.4m^2
I need help with this differential equation.

Answers
(i) The partial fraction decomposition of\(100/(x^7 * (10 - x))\) is\(100/(x^7 * (10 - x)) = 10/x^7 + (1/10^5)/(10 - x).\) (ii) The expression for t in terms of x is t = 10 ± √(100 + 200/x).
(i) To express the rational function 100/(\(x^7\) * (10 - x)) in partial fractions, we need to decompose it into simpler fractions. The general form of partial fractions for a rational function with distinct linear factors in the denominator is:
A/(factor 1) + B/(factor 2) + C/(factor 3) + ...
In this case, we have two factors: \(x^7\) and (10 - x). Therefore, we can express the given rational function as:
100/(\(x^7\) * (10 - x)) = A/\(x^7\) + B/(10 - x)
To determine the values of A and B, we need to find a common denominator for the right-hand side and combine the fractions:
100/(x^7 * (10 - x)) = (A * (10 - x) + B * \(x^7\))/(\(x^7\) * (10 - x))
Now, we can equate the numerators:
100 = (A * (10 - x) + B * \(x^7\))
To solve for A and B, we can substitute appropriate values of x. Let's choose x = 0 and x = 10:
For x = 0:
100 = (A * (10 - 0) + B * \(0^7\))
100 = 10A
A = 10
For x = 10:
100 = (A * (10 - 10) + B *\(10^7\))
100 = B * 10^7
B = 100 / 10^7
B = 1/10^5
Therefore, the partial fraction decomposition of 100/(\(x^7\) * (10 - x)) is:
100/(\(x^7\) * (10 - x)) = 10/\(x^7\) + (1/10^5)/(10 - x)
(ii) Given the differential equation: dx/dt = (1/100) *\(x^2\) * (10 - x)
We are also given x = 1 when t = 0.
To solve this equation and obtain an expression for t in terms of x, we can separate the variables and integrate both sides:
∫(1/\(x^2\)) dx = ∫((1/100) * (10 - x)) dt
Integrating both sides:
-1/x = (1/100) * (10t - (1/2)\(t^2\)) + C
Where C is the constant of integration.
Now, we can substitute the initial condition x = 1 and t = 0 into the equation to find the value of C:
-1/1 = (1/100) * (10*0 - (1/2)*\(0^2\)) + C
-1 = 0 + C
C = -1
Plugging in the value of C, we have:
-1/x = (1/100) * (10t - (1/2)\(t^2\)) - 1
To solve for t in terms of x, we can rearrange the equation:
1/x = -(1/100) * (10t - (1/2)\(t^2\)) + 1
Multiplying both sides by -1, we get:
-1/x = (1/100) * (10t - (1/2)\(t^2\)) - 1
Simplifying further:
1/x = -(1/100) * (10t - (1/2)\(t^2\)) + 1
Now, we can isolate t on one side of the equation:
(1/100) * (10t - (1/2)t^2) = 1 - 1/x
10t - (1/2)t^2 = 100 - 100/x
Simplifying the equation:
(1/2)\(t^2\) - 10t + (100 - 100/x) = 0
At this point, we have a quadratic equation in terms of t. To solve for t, we can use the quadratic formula:
t = (-(-10) ± √((-10)^2 - 4*(1/2)(100 - 100/x))) / (2(1/2))
Simplifying further:
t = (10 ± √(100 + 200/x)) / 1
t = 10 ± √(100 + 200/x)
Therefore, the expression for t in terms of x is t = 10 ± √(100 + 200/x).
For more such questions fraction,click on
https://brainly.com/question/78672
#SPJ8
In exercises 17-20, approximate the logarithm using the properties of logarithms, given the values logb2 = 0.3562, logb3 = 0.5646, and logb = 0.8271. Round your result to four decimal places.
I only need 19 and 20!
19. logb 16/25
20. logb \(\sqrt{3}\)
Answers
The solution of the logarithmic expressions will be:-
19) 2logb4 - 2logb5
20) (1/2)logb (3)
What is an expression?The mathematical expression combines numerical variables and operations denoted by addition, subtraction, multiplication, and division signs.
Mathematical symbols can be used to represent numbers (constants), variables, operations, functions, brackets, punctuation, and grouping. They can also denote the logical syntax's operation order and other properties.
Given that the two expressions are logb 16/25 and logb √3.
The expressions will be solved as:-
E = logb 16/25
E = logb 16 - logb 25
E = logb 4² - logb 5²
E = 2logb 4 - 2logb 5
The second expression will be solved as:-
E = logb √3.
E = ( 1 / 2 ) logb 3
To know more about an expression follow
https://brainly.com/question/20473168
#SPJ1
Given the figure below .find X and Y to three significant digits.Write your answer in the answer box provided below

Answers
Check the picture below.
Make sure your calculator is in Degree mode.
\(\cos(25^o )=\cfrac{\stackrel{adjacent}{x}}{\underset{hypotenuse}{12}}\implies 12\cos(25^o)=x\implies \boxed{10.876\approx x} \\\\[-0.35em] ~\dotfill\\\\ \sin(25^o )=\cfrac{\stackrel{opposite}{z}}{\underset{hypotenuse}{12}}\implies 12\sin(25^o)=z \\\\[-0.35em] ~\dotfill\\\\ \sin(50^o )=\cfrac{\stackrel{opposite}{z}}{\underset{hypotenuse}{y}}\implies y=\cfrac{z}{\sin(50^o)}\implies y=\cfrac{12\sin(25^o)}{\sin(50^o)}\implies \boxed{y\approx 6.62}\)

In a certain video game, there is a mini-game where the main character can choose from a selection of twenty
presents. The presents are wrapped, so the character does not know what is in them. If 7 presents contain money, 3
presents contain gems, 6 presents contain ore, and 4 presents contain fish, what is the probability that the main
character does not choose a present that contains a gem?
Your answer should be an exact decimal value.
The probability of randomly selecting a present that does not contain a gem is
Answers
Answer:
There are a total of 20 presents, and 3 of them contain gems. Therefore, there are 20 - 3 = 17 presents that do not contain gems.
The probability of randomly selecting a present that does not contain a gem is 17/20 = 0.85 or 85%.
hope it helps you...
State an absolute value inequality for each of the following. Then graph each 1. All numbers less than 7 and greater than -7
Answers
All numbers less than 7 and greater than -7:
|x| < 7

i will give Brainiest if you are right

Answers
Answer:
D.
Step-by-step explanation:
The answer is 117
Answer: The answer is not listed
Step-by-step explanation:
15
25
15
23
15
23
17
21
21
19
15
a.) The standard deviation is(round to two decimal places)
b.) The variance is(round to one decimal place)
c.) The range is
Answers
solve for y
2/3+y -1/9=7/9
Answers
Answer: y = 2/9
..............................
I NEED THE ANSWER ASAP
If you were to write the slope-intercept equation for a line that goes through the point (4,-3)--with a slope of -2--what would be the value of b?
y=mx+b
Answers
y=-2x+5 is the slope-intercept equation for a line that goes through the point (4,-3) and 5 is the value of b.
What is Slope of Line?The slope of the line is the ratio of the rise to the run, or rise divided by the run. It describes the steepness of line in the coordinate plane.
The slope intercept form of a line is y=mx+b, where m is slope and b is the y intercept.
The slope of line passing through two points (x₁, y₁) and (x₂, y₂) is
m=y₂-y₁/x₂-x₁
We have to find the slope-intercept equation for a line that goes through the point (4,-3)--with a slope of -2
m=-2
Now let us find the y intercept
-3=-2(4)+b
-3=-8+b
-3+8=b
5=b
Hence, y=-2x+5 is the slope-intercept equation for a line that goes through the point (4,-3) and 5 is the value of b.
To learn more on slope of line click:
https://brainly.com/question/14511992
#SPJ1
please help! (listing BRAINLIST and giving points) :)
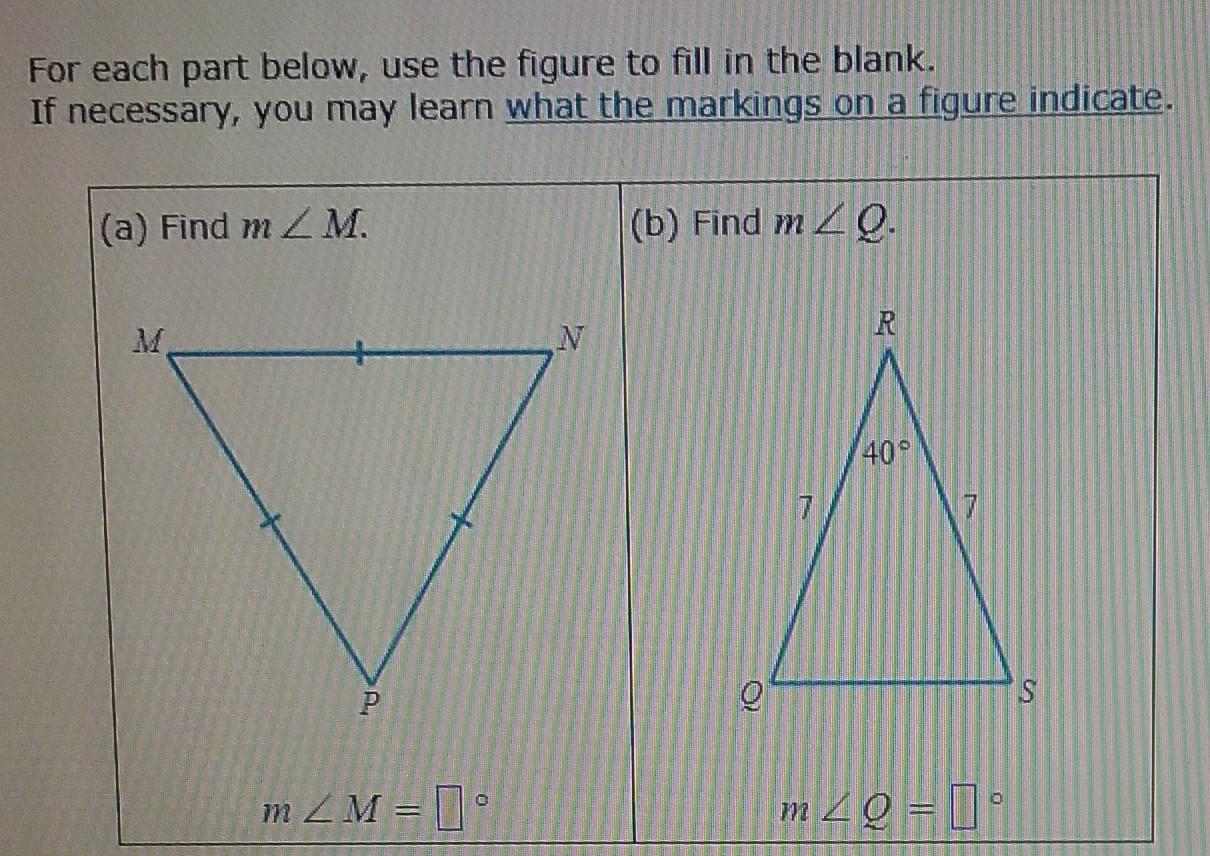
Answers
Answer:
(a) = 60
(b) = 70
Step-by-step explanation:
(a) Sum of all the angles of a triangle is 180
This is an equilateral Triangle
which means all the sides are equal since all the sides are equal that means all the angles are equal
\(x + x + x = 180 \\ 3x = 180 \\ x = \frac{180}{3} \\ x = 60\)
(b) this is an isosceles triangle with two equal sides that means the two opposite angles are equal
\(40 + x + x = 180 \\ 40 + 2x = 180 \\ 2x = 180 - 40 \\ 2x = 140 \\ x = 70\)
The center of a circle is at the origin on a coordinate grid. The vertex of a parabola that opens upward is at (0, 9). If the
circle intersects the parabola at the parabola's vertex, which statement must be true?
O The maximum number of solutions is one.
O The maximum number of solutions is three.
O The circle has a radius equal to 3.
The circle has a radius less than 9.
Answers
As a result, there must be an x value such that the inequality is no longer true, and the parabola and the circle must intersect as a result.
The circle is centered at the origin on a coordinate grid, and the vertex of an upward-opening parabola is located at (0, 9). If the circle has a radius less than 9, the parabola and the circle must intersect.Let's suppose that the upward-opening parabola is y = ax² + 9. Since its vertex is (0, 9), this implies that a > 0, and therefore the parabola opens upwards. Since the circle is centered at the origin and has a radius less than 9, its equation is x² + y² < 81.We can substitute y with ax² + 9 in the inequality x² + y² < 81 and obtain:x² + (ax² + 9)² < 81This simplifies to:(a² + 1) x^4 + 18a² x² + 64 < 0Since the left-hand side of the inequality must be less than zero, it must be negative. Since x² is always non-negative, it follows that a² + 1 > 0. Thus, (a² + 1) x^4 + 18a² x² + 64 < 0 cannot be true for all x
for more search question inequality
https://brainly.com/question/25275758
#SPJ8
A concert promoter must sell 1820 tickets for an upcoming concert. They can sell discount tickets for $40 each, and premium tickets for $45 each, but the total sales must equal $76,300. Let x be the number of discount tickets sold, and y be the number of premium tickets sold. Set up, and solve, the system of equations to find the number of tickets of each type sold.
Give your answer in the form (x, y)
Answers
Answer:
(x, y) = (1120, 700)
Step-by-step explanation:
You want the number of discount (x) and premium (y) tickets to be sold so that a total of 1820 tickets are sold for $40 and $45, respectively, and they generate revenue of $76,300.
EquationsThe equations reflect the relationships stated in the problem:
x + y = 1820 . . . . . . the total number of tickets sold is 1820
40x +45y = 76,300 . . . . . total sales must be $76,300
SolutionIt usually works well to substitute for the variable representing the lower-price tickets:
40(1820 -y) +45y = 76300 . . . . . . substitute for x using the first equation
5y = 3500 . . . . . . . . . . . . . . subtract 72800, simplify
y = 700 . . . . . . . . . . . . divide by 5
x = 1820 -700 = 1120
The numbers of tickets of each type sold are (x, y) = (1120, 700).