Mr. Mole left his burrow that lies below the ground and started digging his way at a constant rate deeper into the ground. Let y represent Mr. Mole's altitude (in meters) relative to the ground after x minutes. Which of the following could be the graph of the relationship?
Answers
Answer:
We know that:
The initial conditions are -7 meters at 0 minutes.
Then, after 6 minutes, he was 16 meters below the ground.
According to these two simple facts we can found the linear function that describes this problem. First, the problem says that Mr. Mole is descending at a constant rate, which is the slope of the function. Now, to calculate the slope we need to points, which are and , where t-values are minutes, and y-values are meters. You can see, that the first point is the initial condition and the second point is 6 minutes later.
So, we calculate the slope:
From the slope we can see that Mr. Mole is descending, because it has a negative sign. Also, the point is on the y-axis, because t is null, so -7 is part of the function. Therefore the function that describes this problem is:
Step-by-step explanation:
Related Questions
Applied (Word) Problems NoteSheet
Consecutive Integers
Consecutive numbers (or more properly, consecutive integers) are integers nrand ngsuch that
/h - nl = I, i.e., IJlfollows immediately after 17,.
Given two consecutive numbers, one must be even and one must be odd. Since the sum of an
even number and an odd number is always odd, the sum of two consecutive numbers (and, in
fact, of any number of consecutive numbers) is always odd.
Consecutive integers are integers that follow each other in order. They have a difference of 1
between every two numbers.
If n is an integer, then n, n+1, and n+2 wi II be consecutive integers.
Examples:
1,2,3,4,5
-3,-2,-1,0,1,2
1004, 1005, 1006
Answers
The concept of consecutive integers is explained as follows:
Consecutive numbers, or consecutive integers, are integers that follow each other in order. The difference between any two consecutive numbers is always 1. For example, the consecutive numbers starting from 1 would be 1, 2, 3, 4, 5, and so on. Similarly, the consecutive numbers starting from -3 would be -3, -2, -1, 0, 1, 2, and so on.
It is important to note that if we have a consecutive sequence of integers, one number will be even, and the next number will be odd. This is because the parity (evenness or oddness) alternates as we move through consecutive integers.
Furthermore, the sum of two consecutive numbers (and, in fact, the sum of any number of consecutive numbers) is always an odd number. This is because when we add an even number to an odd number, the result is always an odd number.
To generate a sequence of consecutive integers, we can start with any integer n and then use n, n+1, n+2, and so on to obtain consecutive integers. For example, if n is an integer, then n, n+1, and n+2 will be consecutive integers.
Here are some examples of consecutive integers:
- Starting from 1: 1, 2, 3, 4, 5, ...
- Starting from -3: -3, -2, -1, 0, 1, 2, ...
- Starting from 1004: 1004, 1005, 1006, 1007, ...
To know more about integers visit-
brainly.com/question/30902406
#SPJ11
FIND THE MISSING SIDE. ROUND TO THE NEAREST TENTH

Answers
Answer:
B, 16.1
Step-by-step explanation:
cos 36 = 13/x
cos 36 × x = 13
x = 13/cos 36
(Use Calculator)
x = 16.068883...
x ≈ 16.1
Find what a equals in this equation.
\(x(x+a)(x+3) = x(x+3)(x-3)\)
Answers
Answer:
a = - 3
Step-by-step explanation:
The equation has common factors x(x + 3) on both sides
For the 2 sides of the equation to be equal, then the factor
(x + a) = (x - 3) and by comparison
a = - 3
let r be the region bounded by the following curves. find the volume of the solid generated when r is revolved about the y-axis. y= sin ^-1 x/9, x=0, y=pi/12 set up the intregral
Answers
The volume of the solid generated when the region R is revolved about the y-axis is given by -π²√3/4 + 18π.
To find the volume of the solid generated when the region bounded by the curves is revolved about the y-axis, we can use the method of cylindrical shells.
First, let's sketch the region R:
Since we have the curves y = asin(x/b), where a = 1 and b = 9, we can rewrite it as \(y = sin^{-1}(x/9)\).
The region R is bounded by \(y = sin^{-1}(x/9)\), x = 0, and y = π/12.
To set up the integral using cylindrical shells, we need to integrate along the y-axis. The height of each shell will be the difference between the upper and lower curves at a particular y-value.
Let's find the upper curves and lower curves in terms of x:
Upper curve: \(y = sin^{-1}(x/9)\)
Lower curve: x = 0
Now, let's express x in terms of y:
x = 9sin(y)
The radius of each shell is the x-coordinate, which is given by x = 9sin(y).
The height of each shell is given by the difference between the upper and lower curves:
\(height = sin^{-1}(x/9) - 0 \\\\= sin^{-1}(9sin(y)/9)\\\\ = sin^{-1}(sin(y)) = y\)
The differential volume element for each shell is given by dV = 2πrhdy, where r is the radius and h is the height.
Substituting the values, we have:
dV = 2π(9sin(y))ydy
Now, we can set up the integral to find the total volume V:
V = ∫[π/12, π/6] 2π(9sin(y))ydy
To find the volume of the solid generated by revolving the region R about the y-axis, we can use the method of cylindrical shells and integrate the expression V = ∫[π/12, π/6] 2π(9sin(y))ydy.
Using the formula for the volume of a cylindrical shell, which is given by V = 2πrhΔy, where r is the distance from the axis of rotation to the shell, h is the height of the shell, and Δy is the thickness of the shell, we can rewrite the integral as:
V = ∫[π/12, π/6] 2π(9sin(y))ydy
= 2π ∫[π/12, π/6] (9sin(y))ydy.
Now, let's integrate the expression step by step:
V = 2π ∫[π/12, π/6] (9sin(y))ydy
= 18π ∫[π/12, π/6] (sin(y))ydy.
To evaluate this integral, we can use integration by parts.
Let's choose u = y and dv = sin(y)dy.
Differentiating u with respect to y gives du = dy, and integrating dv gives v = -cos(y).
Using the integration by parts formula,
∫uvdy = uv - ∫vudy, we have:
V = 18π [(-y cos(y)) - ∫[-π/12, π/6] (-cos(y)dy)].
Next, let's evaluate the remaining integral:
V = 18π [(-y cos(y)) - ∫[-π/12, π/6] (-cos(y)dy)]
= 18π [(-y cos(y)) + sin(y)]|[-π/12, π/6].
Now, substitute the limits of integration:
V = 18π [(-(π/6)cos(π/6) + sin(π/6)) - ((-(-π/12)cos(-π/12) + sin(-π/12)))]
= 18π [(-(π/6)(√3/2) + 1/2) - ((π/12)(√3/2) - 1/2)].
Simplifying further:
V = 18π [(-π√3/12 + 1/2) - (π√3/24 - 1/2)]
= 18π [-π√3/12 + 1/2 - π√3/24 + 1/2]
= 18π [-π√3/12 - π√3/24 + 1].
Combining like terms:
V = 18π [-2π√3/24 + 1]
= -π²√3/4 + 18π.
Therefore, the volume of the solid generated when the region R is revolved about the y-axis is given by -π²√3/4 + 18π.
To learn more about volume of the solid visit:
brainly.com/question/12649605
#SPJ11
question!! if anyone knows!!!

Answers
Your welcome
what is 98 x 47 / 32 x 54?
Answers
Answer:
2837x/16
Step-by-step explanation:
hope this helps - NICK
Answer:
7772.625
Step-by-step explanation:
Given;
\(98\times47\div32\times54\)
Solve;
\(\mathrm{Follow\:the\:PEMDAS\:order\:of\:operations}\)
\(Multiply\:and\:divide\:\left(left\:to\:right\right)\)
\(98\cdot \:47=4606\)
\(=4606\div \:32\cdot \:54\)
\(4606\div \:32=\frac{4606}{32}\)
\(=\frac{4606}{32}\cdot \:54\)
\(=\frac{62181}{8}\)
= 7772.625
~Learn with lenvy~
A simple random sample of 90 is drawn from a normally distributed population, and the mean is found to be 138, with a standard deviation of 34. What is the 90% confidence interval for the population mean? Use the table below to help you answer the question. Confidence Level 90% 95% 99% z*-score 1. 645 1. 96 2. 58 Remember, the margin of error, ME, can be determined using the formula M E = StartFraction z times s Over StartRoot n EndRoot EndFraction. 128. 75 to 147. 25 130. 98 to 145. 02 132. 10 to 143. 90 137. 38 to 138. 62.
Answers
The 90% confidence interval for the population mean of the considered population from the given sample data is given by: Option C: [130.10, 143.90]
How to find the confidence interval for population mean from large samples (sample size > 30)?
Suppose that we have:
Sample size n > 30Sample mean = \(\overline{x}\)Sample standard deviation = sPopulation standard deviation = \(\sigma\)Level of significance = \(\alpha\)Then the confidence interval is obtained as
Case 1: Population standard deviation is known\(\overline{x} \pm Z_{\alpha /2}\dfrac{\sigma}{\sqrt{n}}\)
Case 2: Population standard deviation is unknown.\(\overline{x} \pm Z_{\alpha /2}\dfrac{s}{\sqrt{n}}\)
For this case, we're given that:
Sample size n = 90 > 30Sample mean = \(\overline{x}\) = 138Sample standard deviation = s = 34Level of significance = \(\alpha\) = 100% - confidence = 100% - 90% = 10% = 0.1 (converted percent to decimal).At this level of significance, the critical value of Z is: \(Z_{0.1/2}\) = ±1.645
Thus, we get:
\(CI = \overline{x} \pm Z_{\alpha /2}\dfrac{s}{\sqrt{n}}\\CI = 138 \pm 1.645\times \dfrac{34}{\sqrt{90}}\\\\CI \approx 138 \pm 5.896\\CI \approx [138 - 5.896, 138 + 5.896]\\CI \approx [132.104, 143.896] \approx [130.10, 143.90]\)
Thus, the 90% confidence interval for the population mean of the considered population from the given sample data is given by: Option C: [130.10, 143.90]
Learn more about confidence interval for population mean from large samples here:
https://brainly.com/question/13770164
The volume of calls, V( h), at a particular customer service center can be written as a function of the number of hours after opening each day, h. What would the ordered pair (6,8) represent for this function?
Answers
The ordered pair (6,8) represents the number of calls made after the customer service center opened for 6 hours.
Given that the volume of calls, V( h), at a particular customer service center can be written as a function of the number of hours after opening each day, h. So, (6,8) means that the center has been opened for 6 hours and that there have been 8 calls during this period. It represents the value of the volume of calls V(6) which is 8. Therefore, after opening the customer service center for 6 hours, 8 calls were made.
This function has a direct relationship between the number of hours after opening the center and the number of calls made. Therefore, the longer the center is open, the more calls are expected to be received, and vice versa.
Learn more about ordered pair here:
https://brainly.com/question/30805001
#SPJ11
we have two urns. you can't tell them apart from the outside, but one has seven $1 chips and three $10 chips, and the other has nine $1 chips and one $10 chip. you randomly draw a chip from one of the urns and it happens to be a $10 chip. without replacing this draw, i offer you a chance to draw and keep a chip from either urn. should you draw from the same urn or the opposite urn, and what is the expected value of the chip you draw? why?
Answers
Whether you draw from the same urn or the opposite urn, the expected value of the chip you draw is $2.95. This means that statistically, it doesn't matter which urn you choose to draw from after initially drawing a $10 chip.
The situation involves two urns that appear identical from the outside. However, one urn contains seven $1 chips and three $10 chips, while the other urn contains nine $1 chips and one $10 chip.
Let's consider the scenario where you randomly draw a chip from one of the urns, and it happens to be a $10 chip. After this draw, you are given the opportunity to draw and keep a chip from either urn, without replacing the initial draw.
To determine whether you should draw from the same urn or the opposite urn, we need to calculate the expected value of the chip you draw in each case.
1. Drawing from the same urn:
If you choose to draw from the same urn, there are two possibilities:
- If you initially drew from the urn with seven $1 chips and three $10 chips, the expected value of the chip you draw is (7/10) * $1 + (3/10) * $10 = $4.
- If you initially drew from the urn with nine $1 chips and one $10 chip, the expected value of the chip you draw is (9/10) * $1 + (1/10) * $10 = $1.90.
To calculate the overall expected value when drawing from the same urn, we need to consider the probability of initially drawing from each urn. Since the urns are indistinguishable from the outside, the probability of initially drawing from either urn is 1/2. Therefore, the expected value of drawing from the same urn is (1/2) * $4 + (1/2) * $1.90 = $2.95.
2. Drawing from the opposite urn:
If you choose to draw from the opposite urn, there are also two possibilities:
- If you initially drew from the urn with seven $1 chips and three $10 chips, the expected value of the chip you draw is (9/10) * $1 + (1/10) * $10 = $1.90.
- If you initially drew from the urn with nine $1 chips and one $10 chip, the expected value of the chip you draw is (7/10) * $1 + (3/10) * $10 = $4.
Similarly, considering the probability of initially drawing from each urn (1/2), the expected value of drawing from the opposite urn is (1/2) * $1.90 + (1/2) * $4 = $2.95.
Therefore, whether you draw from the same urn or the opposite urn, the expected value of the chip you draw is $2.95. This means that statistically, it doesn't matter which urn you choose to draw from after initially drawing a $10 chip.
To know more about expected value refer here:
https://brainly.com/question/29068283
#SPJ11
what is the slope of this line

Answers
Answer:
y = 300x + 100
Step-by-step explanation:
y = mx + c
the line intersects the y axis at 100, so c = 100
m = difference between y-coordinates / difference between x-coordinates
m = (400-100)/(1-0) = 300/1 = 300
y = 300x + 100
To test for the significance of a regression model involving 8 independent variables and 220 observations, the numerator and denominator degrees of freedom (respectively) for the critical value of F are _____.
Answers
The critical values of F can be determined from an F-distribution table with 8 and 211 degrees of freedom at the desired level of significance.
To test the significance of a regression model with 8 independent variables and 220 observations, we can perform an F-test using the following null and alternative hypotheses:
Null hypothesis: The regression model is not significant (i.e., all regression coefficients are equal to zero).
Alternative hypothesis: The regression model is significant (i.e., at least one regression coefficient is not equal to zero).
The F-test statistic is calculated as the ratio of the explained variance to the unexplained variance in the model, which follows an F-distribution under the null hypothesis.
The numerator degrees of freedom are equal to the number of independent variables in the model (8), and the denominator degrees of freedom are equal to the total number of observations minus the number of independent variables minus 1 (220 - 8 - 1 = 211).
for such more question on F-distribution
https://brainly.com/question/25573309
#SPJ11
Solve for x please thanks
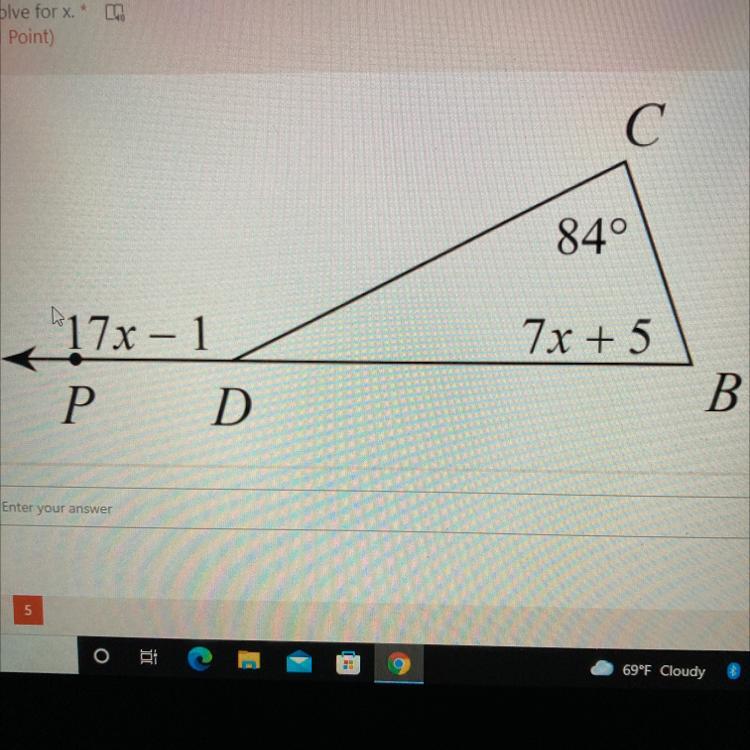
Answers
Answer:
x = 9
Step-by-step explanation:
Angle PDC is an exterior angle. There is a theorem that says it is equal to the two angles (C and B) added together.
17x - 1 = 7x + 5 + 84
17x - 1 = 7x + 89
Subtract 7x
10x - 1 = 89
Add 1
10x = 90
Divide by 10
x = 9
Some of Mrs. Turay’s eighth graders took the PSAT test. Score totals of ten of her students are below. Calculate the mean and the median, and determine which provides a better view of the score data.
Scores:
60, 62, 67, 69, 70, 70, 71, 75, 76, 120
The mean test score total is .
The median test score total is .
Which measure of center best represents the test data?
Answers
Answer:
The mean test score total is
✔ 74
The median test score total is
✔ 70
Which measure of center best represents the test data?
✔ median
Step-by-step explanation:
sorry if im late but i hope this helps :)
If lunch cost $15.70, before tip, and you left $3.14, what %
tip did you leave and what was the total cost of lunch?
Answers
Answer:
20%
$18.84
Step-by-step explanation:
3.14 is what percent of 15.70?
Use the percent-to-dollar conversion (100: 15.70) :
3.14 * 100% / 15.70 =
3.14 / 15.70 * 100% =
1/5 * 100% =
100% / 5 = 20% ==> percent tip
$15.70 + $3.14 = $18.84 ==> Total cost
An angle measures 122 degrees more than the measure of its supplementary angle. what is the measure of each angle
Answers
Answer:
58 for the opposite angle and 180 for the regular angle
7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17 and 18 Use Part 1 of the Fundamental Theorem of Calculus to find the derivative of the function. 7 g(x) = { vt ++3 dt Jo Answer 8. g(x) = {* In (1+tº) dt
Answers
By using Fundamental Theorem of Calculus, we find the derivative of the function g(x) = In { sqrt( t + t^3)dt } limit from x to 0 is ln(sqrt(x + x^3)). The derivative of the function g(x) = { In (1+t^2) dt} where limit are from x to 1 is ln(1 + x^2).
The Fundamental Theorem of Calculus, which states that if a function is defined as the definite integral of another function, then its derivative is equal to the integrand evaluated at the upper limit of integration.
So, applying this theorem, we have:
g'(x) = d/dx [∫x_0 ln(sqrt(t + t^3)) dt]
= ln(sqrt(x + x^3)) * d/dx (x) - ln(sqrt(0 + 0^3)) * d/dx (0)
= ln(sqrt(x + x^3))
Therefore, g'(x) = ln(sqrt(x + x^3)).
Using the Fundamental Theorem of Calculus, we have:
g'(x) = d/dx [∫1_x ln(1 + t^2) dt]
= ln(1 + x^2) * d/dx (x) - ln(1 + 1^2) * d/dx (1)
= ln(1 + x^2)
Therefore, g'(x) = ln(1 + x^2).
To know more about Fundamental Theorem of Calculus:
https://brainly.com/question/30761130
#SPJ4
____The given question is incomplete, the complete question is given below:
Use Part 1 of the Fundamental Theorem of Calculus to find the derivative of the function. 7 g(x) = In { sqrt( t + t^3)dt } limit from x to 0. 8. g(x) = { In (1+t^2) dt} where limit are from x to 1.
An Arrow-Debreu security pays $1 at expiry node (6,2). The upstate risk neutral probability is π=0.4 and the return over one time-step is R=1.05. What is the premium of this Arrow-Debreu security?
Answers
The value of the Arrow-Debreu security is calculated as the present value of its expected payoff, discounted at the risk-neutral rate. As a result, the premium of the Arrow-Debreu security can be computed using the following formula: \($P_{t}=\frac{1}{(1+R)^{n-t}}\times \pi$,\)
where π=0.4, R=1.05, n=6, and t=2 (expiry node).
By substituting the values, we obtain:
\($P_{2}=\frac{1}{(1+1.05)^{6-2}}\times 0.4 = \frac{0.4}{(1.05)^4} \approx 0.3058$.\)
Therefore, the premium of the Arrow-Debreu security is approximately $0.3058.
Arrow-Debreu securities are typically utilized in financial modeling to simplify the pricing of complex securities. They are named after Kenneth Arrow and Gerard Debreu, who invented them in the 1950s. An Arrow-Debreu security pays $1 if a particular state of the world is realized and $0 otherwise.
They are generally utilized to price derivatives on numerous assets that can be broken down into a set of Arrow-Debreu securities. The value of an Arrow-Debreu security is calculated as the present value of its expected payoff, discounted at the risk-neutral rate. In other words, the expected value of the security is computed using the risk-neutral probability, which is used to discount the value back to the present value.
The formula is expressed as:
\($P_{t}=\frac{1}{(1+R)^{n-t}}\times \pi$\),
where P_t is the price of the Arrow-Debreu security at time t, π is the risk-neutral probability of the security’s payoff, R is the risk-free rate, and n is the total number of time periods.However, Arrow-Debreu securities are not traded in real life. They are used to determine the prices of complex securities, such as options, futures, and swaps, which are constructed from a set of Arrow-Debreu securities.
This process is known as constructing a complete financial market, which allows for a more straightforward pricing of complex securities.
The premium of the Arrow-Debreu security is calculated by multiplying the risk-neutral probability of the security’s payoff by the present value of its expected payoff, discounted at the risk-neutral rate.
The formula is expressed as
\($P_{t}=\frac{1}{(1+R)^{n-t}}\times \pi$,\)
where P_t is the price of the Arrow-Debreu security at time t, π is the risk-neutral probability of the security’s payoff, R is the risk-free rate, and n is the total number of time periods. Arrow-Debreu securities are not traded in real life but are used to price complex securities, such as options, futures, and swaps, by constructing a complete financial market.
To know more about risk-neutral probability :
brainly.com/question/32719566
#SPJ11
a certain dj takes requests for songs at a party. assume that there are 120 people at the party, each of whom makes exactly one request for a song. all of their requests are made independently. assume that each person asks for a pop song with probability 0.37, a rock song with probability 0.2, or a rap song with probability 0.43. what is the probability that 50 or more requests are made for pop songs?
Answers
the probability that 50 or more requests are made for pop songs is 0.0967, or about 9.67%.
Define binomial distributionThe binomial distribution is a probability distribution that describes the number of successes in a fixed number of independent trials, where each trial has the same probability of success.
We can use the binomial distribution to model this situation, where the number of trials is 120 (the number of people at the party), and the probability of success (making a request for a pop song) is 0.37. Let X be the number of requests for pop songs. Then:
The mean of X is μ = np = 120 x 0.37 = 44.4
The standard deviation of X is σ = sqrt(np(1-p)) = sqrt(120 x 0.37 x 0.63) = 4.32
To find the probability that 50 or more requests are made for pop songs, we can use the normal approximation to the binomial distribution, which applies when np >= 10 and n(1-p) >= 10.
Let Z be a standard normal random variable, then:
P(X >= 50) = P((X - μ)/σ >= (50 - μ)/σ)
= P(Z >= (50 - 44.4)/4.32)
= P(Z >= 1.2963)
= 1 - P(Z < 1.2963)
= 1 - 0.9033
= 0.0967
Therefore, the probability that 50 or more requests are made for pop songs is approximately 0.0967, or about 9.67%.
To know more about variables, visit:
https://brainly.com/question/17344045
#SPJ1
Need help ASAP PLEASE AND SHOW WORk DUE SOON !!!

Answers
Answer: Wrong formula, forgot to input the radius instead
Step-by-step explanation:
Formula is pie times radius^2
Find radius by dividing the diameter by half then multiplying it by pi (3.14)
6 milimeters is equil to how many meters?
Answers
Answer:
0.006 m
Step-by-step explanation:
There are 1,000 millimeters in one meter.
6/1,000= 0.006 m
Determine whether the study is an observational study or an experiment.
Research is conducted to determine if there is a relation between hearing loss and exposure to mumps. Does the description correspond to an observational study or an experiment?
Answers
Researchers are observing those with mumps to see how it affects hearing loss at all. There may be strong correlation, weak correlation, or no correlation at all.
With an experiment, researchers would break the participants into two groups: control group and treatment group. Those in the control group get the placebo (fake treatment) while the treatment group gets the treatment applied to them. If we were dealing with an experiment for this context, then the treatment group would get exposed to mumps on purpose. Of course, this is unethical and dangerous so an experiment for this type of project is not a good idea. It's better to go with an observational study.
Range of g(x)=3 square root of x

Answers
The range of the function g(x) is given as follows:
[0, ∞).
How to obtain the domain and range of a function?The domain of a function is obtained as the set containing all the values assumed by the independent variable x of the function, which are also all the input values assumed by the function.The range of a function is obtained as the set containing all the values assumed by the dependent variable y of the function, which are also all the output values assumed by the function.From the graph of the function given in this problem, y assumes all real non-negative values, hence the interval notation representing the range of the function is given as follows:
[0, ∞).
Learn more about domain and range at https://brainly.com/question/26098895
#SPJ1
3.) Given the equation for the graph of
f(x) = |x|, describe in words the
transformations necessary to create
the equation for the graph of g(x) then
write the equation for g(x).

Answers
Answer:
thxfh*ghtcvbnv =fbyfc
A rectangle has a length of 25 feet and a width of 18 feet what is the area model of the rectangle
Answers
Answer:
450 sq.feet
Step-by-step explanation:
Given,
Length ( l ) = 25 feet
Width ( b ) = 18 feet
To find :
Area ( rectangle ) = ?
Formula : -
Area ( rectangle ) = l x b
Area ( rectangle )
= 25 x 18
= 450 sq.feet
Check photo for work
I will mark right answer brainy thing

Answers
Answer: D
Step-by-step explanation:
Answer: D
Step-by-step explanation:
We are trying to find out how this situation leads to 30 miles for d.
We know he has 14 miles to the gas station, and he has gone an unknown amount in 2 hours, t.
30=Xt+14
Solving for X: 30=X(2)+14
X=8
What is the area of the obtuse triangle given below? A. 21 sq. units B. 98 sq. units C. 49 sq. units D. 28 sq. units 7 14 Kand)
Answers
The area of an obtuse triangle can be found using the formula: Area = (1/2) * base * height.
To find the base and height of the triangle, we need to identify a right angle within the triangle. One way to do this is by drawing an altitude from one vertex to the opposite side.
Once we have the right angle, we can determine the base and height. The base is the length of the side to which the altitude is drawn, and the height is the length of the altitude itself.
Unfortunately, the given information does not provide any measurements or angles of the triangle. Therefore, we cannot calculate the area of the obtuse triangle accurately. Hence, the answer cannot be determined with the given information.
To know more about Triangles visit.
https://brainly.com/question/2773823
#SPJ11
PLEASE HELP ALMOST DUE BRANILIEST AND 5 STARTS AND A THANKS PLSLSLSLSL

Answers
Answer:
c = -72
Step-by-step explanation:
Subtract 6 from both sides (14 - 6 = 8)
c/-9 = 8
Multiply -9 to both sides to isolate c (8 * -9 = -72)
c = -72
Deondra has $12 to spend on a mixture of green and red grapes. What equation can she use to graph a line showing the different amounts of green and red grapes she can buy for $12?
Answers
Answer:
It depends on the cost of grapes.
Step-by-step explanation:
Half of 12 is 6, so if each pack of grapes cost 6 or less, she can buy a pack of green and red grapes.
The equation that Deondra can use to graph the line showing different amounts of green and red grapes she can buy for $12 is :
ax + by = 12
Let the number of green grapes be a
Let the cost of one green grape be x
Let the number of red grapes be b
Let the cost of one red grape be y
The total cost of green and red grapes = $12
The equation representing the illustration will be of the form:
(Number of green grapes)(Cost of 1 green grape) +
(Number of red grapes)(cost of 1 red grape) = Total cost
The equation that Deondra can use to graph the line showing different amounts of green and red grapes she can buy for $12 is therefore:
ax + by = 12
Learn more here: https://brainly.com/question/17896524
Please I nee help....

Answers
The area of the figure is 39 feet square.
How to find the area of a composite figure?A composite figure contains two or more shapes. The figure above is a composite figure. The area of the figure can be calculated as follows:
area of the figure = area of rectangle 1 + area of rectangle 2
Therefore,
area of rectangle 1 = lw
where
l = lengthw = widthTherefore,
area of rectangle 1 = 2(3)
area of rectangle 1 = 6 ft²
area of rectangle 2 = 11 × 3
area of rectangle 2 = 33 ft²
Therefore,
area of the figure = 6 + 33
area of the figure = 39 ft²
learn more on area here: brainly.com/question/15434045
#SPJ1
is 2(6-3x)+x equivalent to 2(3x)+x
Answers
Answer: yes i think they are
Step-by-step explanation:
hope it helps:)
Answer
2(6−3x)+x=−5x+12
2(3x)+x=7x