Module 4: HW - Paired t-test Setup (Try 2)
<< Statistics >>
There are 9 data pairs. In the test, subtract the First
Value from the Second Value. Also, Δ0 = 0
1 Pair 2 WN 3 456780 A 9 10 B с First Value Second Valu 1 2.45 0.5 1.43 -5.34 3.68 8.4 -3.29 4.18 -5.14 2.03 -1.49 7.44 4.44 8.1 -0.68 5.58 4.13 3.53 N345 2 6700 8 9
Question 4 Compute d -8.454 O -7
Answers
A paired t-test can be defined as a statistical test that is utilized to compare the means of two related sets of samples. The data consists of nine pairs, and the initial value is subtracted from the second value.Δ0 = 0 is also given. As a result, the question is "Compute d."Here, first,The value of d is -0.27680007490074524.Answer: d = -0.27680007490074524.
we need to calculate the difference between the first and second values of each pair of data.
The differences of the given data are as follows: Pair Differences1 -1.95 2.2 -0.29 -9.02 4.17 -0.96 7.73 -4.47 -1.47
We need to compute d.
The formula to calculate d is as follows: d = (Mean of Differences - Δ0)/Standard Deviation of Differences Mean of Differences = Sum of Differences / Number of Differences= (-1.95 + 2.2 - 0.29 - 9.02 + 4.17 - 0.96 + 7.73 - 4.47 - 1.47) / 9 = -0.7377777777777779Δ0 = 0
Standard Deviation of Differences can be calculated by using the following formula
:= SQRT[∑(Di - D.mean)² / (n-1)]
Where Di is the ith difference and D.mean is the mean of all differences.∑(Di - D.mean)² = [(-1.95 - (-0.7377777777777779))^2 + (2.2 - (-0.7377777777777779))^2 + (-0.29 - (-0.7377777777777779))^2 + ... + (-1.47 - (-0.7377777777777779))^2] = 53.22602469135803So,
Standard Deviation of Differences= SQRT[53.22602469135803 / (9 - 1)] = 2.6602176018815615So, d = (-0.7377777777777779 - 0) / 2.6602176018815615= -0.27680007490074524.
The value of d is -0.27680007490074524.
Answer: d = -0.27680007490074524.
To know more about Standard Deviation of Differences visit:
https://brainly.com/question/15319829
#SPJ11
Related Questions
Graham sold 6 magazines less than double what Adrianne sold, which of the following expressions represents graham’s sales? ( 9th grade, Algebra 1 )
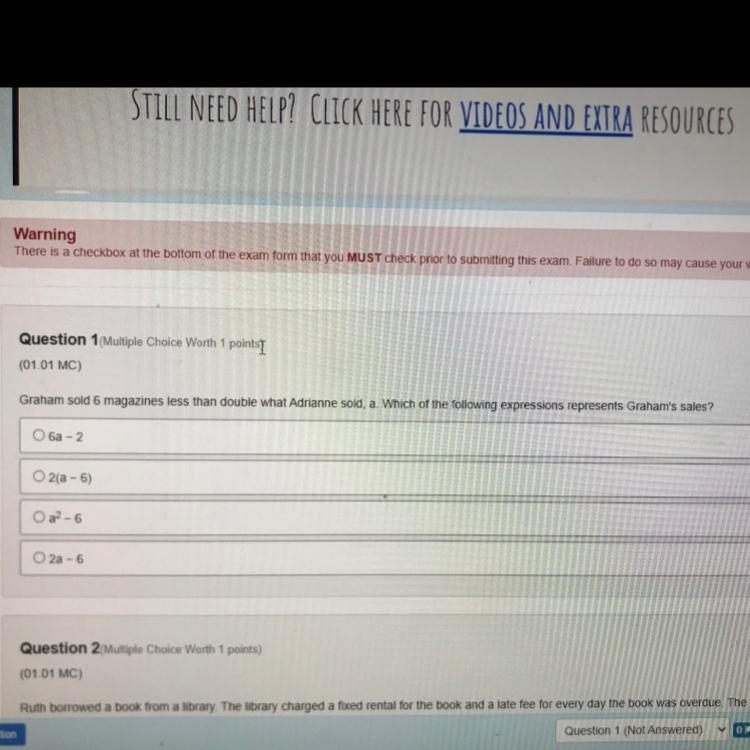
Answers
Answer:
The expression that represents Graham's sales is: 2a - 6
Graph the line that passes through the two points.
(0, 0), (3, 3)
Line
Undo
Redo
Х
3
2
1
-3
-2
-1
0
1
2
13
-1
-2-
-3
Find the slope of the line.
slope =

Answers
Answer:
Graph attachedSlope is 7Step-by-step explanation:
First plot the two points on the graph (0, 0) and (1/3, 7/3)
Then connect those points by a line and extend the line
See attached
Slope is:
m = 7/3 : 1/3 = 7/3*3 = 7
Write an explicit formula for an, the nth term of the sequence 112, -28, 7, ....
Answers
Answer:
\(a_n=112\left(-\frac{1}{4}\right)^{n-1}\)
Step-by-step explanation:
Geometric Sequences
There are two basic types of sequences: arithmetic and geometric. The arithmetic sequences can be recognized because each term is found as the previous term plus a fixed number called the common difference.
In the geometric sequences, each term is found by multiplying (or dividing) the previous term by a fixed number, called the common ratio.
We are given the sequence:
112, -28, 7, ...
It's easy to find out this is a geometric sequence because the signs of the terms are alternating. If it was an arithmetic sequence, the third term should be negative like the second term.
Let's find the common ratio by dividing each term by the previous term:
\(\displaystyle r=\frac{-28}{112}=-\frac{1}{4}\)
Testing with the third term:
\(\displaystyle -28*-\frac{1}{4}=7\)
Now we're sure it's a geometric sequence with r=-1/4, we use the general equation for the nth term:
\(a_n=a_1*r^{n-1}\)
\(a_n=112\left(-\frac{1}{4}\right)^{n-1}\)
(1 point) Evaluate ∫∫S1+x2+y2−−−−−−−−−√dS
∫
∫
S
1
+
x
2
+
y
2
d
S
where S
S
is the helicoid: r(u,v)=ucos(v)i+usin(v)j+vk
r
(
u
,
v
)
=
u
cos
(
v
)
i
+
u
sin
(
v
)
j
+
v
k
, with 0≤u≤2,0≤v≤3π
Answers
Answer:
The value of the surface integral is 2π.
Step-by-step explanation:
We have the helicoid given by the parameterization:
r(u,v) = u cos(v) i + u sin(v) j + v k, with 0 ≤ u ≤ 2, 0 ≤ v ≤ 3π.
The surface integral to evaluate is:
∫∫S √(1 + x² + y²) ds
We can compute this integral using the formula:
∫∫Sf( x , y, z ) ds = ∫∫T f(r(u,v)) ||ru × rv|| du dv,
where T is the region in the uv-plane corresponding to S, and ||ru × rv|| is the magnitude of the cross product of the partial derivatives of r with respect to u and v.
In our case, we have:
f( x , y, z ) = √(1 + x² + y²) = √(1 + u²),
r(u ,v) = u cos(v) i + u sin(v) j + v k,
ru = cos(v) i + sin(v) j + 0 k,
rv= -u sin(v) i + u cos(v) j + 1 k,
ru × rv = (-sin(v)) i + cos(v) j + u k,
||ru x rv || = √(sin²(v) + cos²(v) + u²) = √(1 + u²).
Thus, the integral becomes:
∫∫S √(1 + x² + y²) ds = ∫∫T √(1 + u²) √(1 + u²) du dv
= ∫∫T (1 + u²) du dv
= ∫0^(3π) ∫0^2 (1 + u²) u du dv
= ∫0^(3π) [(1/2)u² + (1/3)u³]_0^2 dv
= ∫0^(3π) (2/3) dv
= (2/3) (3π - 0)
= 2π.
Therefore, the value of the surface integral is 2π.
To know more about helicoid refer here
https://brainly.com/question/31954311#
#SPJ11
What the answer now and answer fast correct answer

Answers
Answer:
Using the given information in the problem, the value of f is 9
Step-by-step explanation:
In this problem, we will be using tangent, Tangent is the opposite side divided by the adjacent side from the given angle. The given angle that we will be using for this problem is the measurement of ∠F which is 58°. We will use this for our equation.
Let's set up our equation for tangent.
\(Tan(58)=\frac{15}{f}\)
Since we are looking for f , then we will rearrange the equation.
\(f=\frac{15}{tan(58)}\)
Now, we will solve for x. You can use a calculator to do these calculations.
\(f=9\)
So, the value of f in the triangle is 9.
Answer: f=9
Because quick mafs says so
Which type of data would be considered qualitative data?
Answers
The type of data which would be considered as the qualitative data is the smell of the plant.
What is qualitative data?
The qualitative data is the data which describes the quality or the characteristics of a thing.
Qualitative data can be felt rather than measure. The data of color of hairs of cricket team player is an example of qualitative data.
The options for the problem are listed below.
Mass of a plant- It is a type of quantitative data which can be measured in kg.Height of a plant-This type of data is quantitative data which can be measured in m or ft.Smell of a plant-The smell of a plant can be filled and considered as qualitative data. Volume of water-This is also a type of quantitative data.Thus, the type of data which would be considered as the qualitative data is the smell of the plant.
Learn more about the qualitative data here
https://brainly.com/question/24492737
Seven different names were put into a hat. A name chosen 100 times. And the name Michael is chosen 9 times. What is experimental probability of the name Michael being chosen? What is the theoretical probability of the name Michael being chosen? Use the pencil and paper. Explain how each probability would change if the number of names in the hat were different.
Answers
Answer:
Experimental probability = 9 / 100
Theoretical probability = 1/7
Step-by-step explanation:
The experimental probability of an event is written as :
P = number of times event occur / total number of trials
Experimental probability is based on the outcome of an experiment that has taken place.
Theoretical probability is based on expected outcome of an event.
P = number of expected or required outcomes / total possible outcomes
Experimental probability of choosing the name Michael is :
Number of times Michael is chosen / number of trials
Experimental probability = 9 / 100 = 0.09
Theoretical probability of choosing michael:
Number of names in hat = 7
Number of names called Michael in hat = required outcome = 1
P = 1 / 7
If the number of names in hat was different from 7, then the theoretical probability will change.
Also, if the number of times a name was chosen was different from 100, then number of trials will also change and hence, the experimental probability.
Two pieces of ribbon, one with a length of 63 inches and another with a length of 42 inches are cut into pieces of equal length without remainder. Find the greatest possible length that the pieces can be.
Answers
Answer
224 over 567
Step-by-step explanation:
Answer:
21
Step-by-step explanation:
the greatest possible length that the two ribbons would be when the ribbons are divided by their lowest common multiple.
The lowest common multiple of 63 is 3. 63/3 = 21
The lowest common multiple of 42 is 2 = 42/2 = 21
ZA and ZB are vertical angles. If m≤A = (7x + 4)° and m
ZB = (8x − 20)°, then find the measure of ZB.
Answers
Answer:
mAngleB = 172°
Step-by-step explanation:
"vertical angles" means that the angles are equal to each other.
We can write an equation:
7x + 4 = 8x - 20
subtract 7x from both sides.
4 = x - 20
add 20 to both sides
24 = x
Then, the question asks for the measure of AngleB.
AngleB
= 8x - 20
= 8(24) - 20
= 192 - 20
= 172
mAngleB = 172°
Does the graph of the function ever cross the x-axis?
Answers
Yes, the graph of the function do cross the x-axis.
X-intercept . The x-intercept marks the location at which the graph crosses the x-axis, or (a,0). When y is 0, the x-intercept appears. The graph's intersection with the y-axis, or point (0,b), is known as the y-intercept. When x is 0, the y-intercept appears.
The x-intercept and y-intercept are the points at which a line crosses the x- and y-axes, respectively.
The y-axis is typically the vertical axis, while the x-axis is typically the horizontal axis. The figure below illustrates how they are represented by two number lines that perpendicularly intersect at (0, 0), the origin.
To learn more about the x-intercept click here:
brainly.com/question/14180189
#SPJ4
simplify.
remove all perfect squares from inside the square roots. assume x and y are positive.
√8x^3y^2
Answers
Answer:
\(2xy\sqrt{2x}\)
Step-by-step explanation:
Because this is a whole term in itself (no addition or subtraction), you can just directly find squares and factor them out. First, when looking at 8, you can factor out 4, to get 2 on the outside. Then, while looking at x cubed, you can factor out x squared, to get x on the outside, and when looking at y squared, you can just pull that outside itself, to get y. Now, we have one 2 and one x remaining, for a total of \(2xy\sqrt{2x}\)
if two medians of a triangle are equal ,proof that the triangle formed by a segment of the median and the third side is an isosceles triangle
Answers
Let the triangle be ABC, and where the medians AD and BE intersect be M.
The three medians intersect at the centroid, and divide each other in the ratio 1:2
That means that AM = BM and the triangle ABM is isosceles.
Chi-square distributions that are positively skewed have a research hypothesis that is?
Answers
Answer:
A one tailed test
Step-by-step explanation:
Chi-Square Distributions That Are Positively Skewed Have A Research Hypothesis That Is A One-Tailed Test.
Chi-Square distributions are positively skewed, with the degree of skew decreasing with increasing degrees of freedom.
#SPJ4
learn more on chi square
https://brainly.com/question/14082240
One-Tailed Test
In probability theory and statistics, the chi-square distribution with k degrees of freedom is the distribution of the sum of squares of k independent standard normal random variables. The chi-square distribution is a continuous probability distribution. The shape of the chi-square distribution depends on its degrees of freedom k. It is used to describe the distribution of the sum of squares of random variables. The chi-square distribution is positively skewed, with decreasing skewness as the degrees of freedom increase. The chi-squre distribution approaches the normal distribution on increase of degree of freedom.Chi-Square distributions that are positively skewed have a research hypothesis that is a One-Tailed Test.
Learn more about chi-square distribution
https://brainly.com/question/4543358
#SPJ4
The prism below is made of cubes which measure 1/2 of an inch on one side. What is the volume?

Answers
Answer: 24 I think if not my bad
Step-by-step explanation:
If I recall right you just have to count them
determine whether each sequence below converges or diverges. if the sequence converges, find its limit. carefully show your work! (a) an
Answers
The given sequence converges to zero
Why a sequence converges to 0?
The given sequence is {an}n = 1∞ = 1/ (n + 3).
The task is to find whether the sequence converges or diverges.
If it converges, then we have to determine the limit of the given sequence.
The general term of the sequence is given by,
an = 1/ (n + 3) ...[1]
The given sequence is
{an}n = 1∞ = 1/ (n + 3).
For the given sequence, let us check whether it is converging or diverging.
To determine if the sequence converges or diverges, we take the limit of the sequence.
Let, L = limit of sequence.
Then,
lim n→∞an = lim n→∞1/ (n + 3)
Put n = ∞ in [1].
an = 1/ (n + 3)an = 1/ (∞ + 3) = 0L = 0.
Hence,
lim n→∞an = 0.
Since limit exists, we can say that the sequence is convergent.
If the sequence is convergent, then we can find its limit.
To find the limit of the sequence, we can directly write the value of the limit.
L = 0.
Hence, the given sequence converges to zero.
Learn more about sequence converges
brainly.com/question/21961097
#SPJ11
Solve for z in -3 < z-1 < 3.Give the result in the interval notation and graph on a number line
Answers
Answer:
(-2,4)
Explanation:
Given the inequality:
\(-3First, we add 1 to all parts of the inequality.\(\begin{gathered} -3+1We can represent this in interval notation as:\((-2,4)\)The solution set is graphed on the number line below:

SOMEONE HELP PLEASEEE (the photo is attached <3)

Answers
Answer:
C. 25
Step-by-step explanation:
Lets just first do 5-² = .04
So it will look like this
\(\frac{1}{1/25}\) To do this all you have to do is flip 1/25 to 25/1 so that you can multiply instead on divide.
It will look like this
.\(\frac{1}{1}*\frac{25}{1}=\frac{25}{1}\) = 25
Sorry I took so long hope this helps!!
sophie can type 128 words in 3 minutes. how many words can she type in an hour?
Answers
Answer:
3x128 = 384
Step-by-step explanation:
PLEASE HELP ME JUST NEED TO ANSWER A OR B OR BOTH IF U WANT

Answers
Answer: Part A - 113°
Step-by-step explanation:
A. 6x-5 = 5x+7 -> x = 12
6x-5 -> 6(12)-5 = 72-5 = 67
180-67 = 113
Solve: 7(2W + 10) = 84
O w = 1
O w = 2
O w = 21
O w = 70
plz help

Answers

لیا
The prism below is made of cubes which measure 1/4 of a centimeter on one side. What is the volume?
Answers
Answer:
Below
Step-by-step explanation:
You didn't include the picture......
each cube has a volume of 1/4 * 1/4 * 1/4 = 1/64 cm^3
count the total number of cubes and multiply by 1/64
to get volume in cm^3
Translate this sentence into an equation.
24 is the product of Donnie's score and 2.
Use the variable d to represent Donnie's score.
Answers
Answer:
24 = 2d
Step-by-step explanation:
24 is (=) the product (×) of Donnie's score (d) and 2.
24 = 2d
Find a power series solution of the differential equation given below. Determine the radius of convergence of the resulting series, and use the series given below to identify the series in terms of familiar elementary functions.
2(x-1)y' = 7y
(1)The power series solution is y(x) = _________ + .... (up to order of 3)
(2) The radius of convergence of the series is _____
(3) The series solution in terms of familiar elementary functions is y(x) = _________
Answers
The power series of a differential equation with y(x) as the sum of a power series that is,
\(y(x) = ∑_(n=0)^∞▒〖a_n(x-c)^n 〗\)
The radius of convergence of the series is infinity.
The series solution in terms of familiar elementary functions is given by,\(y(x) = 3 x^(7/2)/(√14)\)
This equation has the initial condition y(1) = 3.
Substituting the power series into the differential equation and solving for the coefficient of each power of (x - 1) provides a recursive formula that we can use to determine each coefficient of the power series representation.
2(x - 1)y' = 7y ⇒ y' = 7y/2(x - 1)
Taking the first derivative of the power series, we get,\(y'(x) = ∑_(n=1)^∞▒〖na_n(x-c)^(n-1) 〗\)
Using this, the above differential equation becomes\(,∑_(n=1)^∞▒〖na_n(x-c)^(n-1) 〗 = 7/2\)
\(∑_(n=0)^∞▒a_n(x-c)^n〖- 7/2 ∑_(n=0)^∞▒a_n(x-c)^n〗⇒ ∑_(n=1)^∞▒〖na_n(x-c)^(n-1) 〗= ∑_(n=0)^∞▒〖(7/2 a_n - 7/2 a_(n-1)) (x-c)^n〗\)
Since the two power series are equal, the coefficients of each power of (x - 1) must also be equal.
Therefore,\(∑_(k=0)^n▒〖k a_k (x-c)^(k-1) 〗= (7/2 a_n - 7/2 a_(n-1))\)
The first few terms of the series for the power series solution y(x) is given by,
\(y(x) = 3 + 21/4 (x - 1) + 73/32 (x - 1)^2 + 301/384 (x - 1)^3,\) to the order of 3.
To know more about differential equation visit:
https://brainly.com/question/32645495
#SPJ11
solve the equation
pic:

Answers
The solution to the equation \((\sum\limits^{\infty}_{i=1} \frac{1}{2^i}) + (\sum\limits^{\infty}_{i=1} \frac{9}{10^i}) + \sin^2(\theta) + \cos^2(\theta) + e^2\) is 10.3891
How to solve the equationFrom the question, we have the following parameters that can be used in our computation:
\((\sum\limits^{\infty}_{i=1} \frac{1}{2^i}) + (\sum\limits^{\infty}_{i=1} \frac{9}{10^i}) + \sin^2(\theta) + \cos^2(\theta) + e^2\)
Using the following trigonometry ratio
sin²(x) + cos²(x) = 1
We have
\((\sum\limits^{\infty}_{i=1} \frac{1}{2^i}) + (\sum\limits^{\infty}_{i=1} \frac{9}{10^i}) + \sin^2(\theta) + \cos^2(\theta) + e^2 = (\sum\limits^{\infty}_{i=1} \frac{1}{2^i}) + (\sum\limits^{\infty}_{i=1} \frac{9}{10^i}) + 1 + e^2\)
The sum to infinity of a geometric series is
S = a/(1 - r)
So, we have
\((\sum\limits^{\infty}_{i=1} \frac{1}{2^i}) + (\sum\limits^{\infty}_{i=1} \frac{9}{10^i}) + \sin^2(\theta) + \cos^2(\theta) + e^2 = \frac{1/2}{1 - 1/2} + \frac{9/10}{1 - 1/10} + 1 + e^2\)
So, we have
\((\sum\limits^{\infty}_{i=1} \frac{1}{2^i}) + (\sum\limits^{\infty}_{i=1} \frac{9}{10^i}) + \sin^2(\theta) + \cos^2(\theta) + e^2 = 1 + 1 + 1 + e^2\)
Evaluate the sum
\((\sum\limits^{\infty}_{i=1} \frac{1}{2^i}) + (\sum\limits^{\infty}_{i=1} \frac{9}{10^i}) + \sin^2(\theta) + \cos^2(\theta) + e^2 = 3 + e^2\)
This gives
\((\sum\limits^{\infty}_{i=1} \frac{1}{2^i}) + (\sum\limits^{\infty}_{i=1} \frac{9}{10^i}) + \sin^2(\theta) + \cos^2(\theta) + e^2 = 10.3891\)
Hence, the solution to the equation is 10.3891
Read more about summation notation at
brainly.com/question/15973233
#SPJ1
Express the ratio below in its simplest form.
9:9:3
Answers
Answer:3:3:1
Step-by-step explanation:divide by 3
what is the arc length of an arc with a central angle of 11pi/6 radians in a circle with a radius of 18cm? round the nearest whole number. show all work

Answers
The measure of the arc length of the sector will be 103.62 centimeters.
What is the arc length of the sector?Let r be the radius of the sector and θ be the angle subtends by the sector at the center. Then the arc length of the sector of the circle will be
Arc = (θ/2π) 2πr
The central angle is 11π / 6 radian and the radius is 18 cm. Then the measure of the arc length is given as,
Arc = {(11π / 6)/2π} 2π (18)
Arc = 0.9167 x 2 x 3.14 x 18
Arc = 103.62 cm
The measure of the arc length of the sector will be 103.62 centimeters.
More about the arc length of the sector link is given below.
https://brainly.com/question/15955580
#SPJ1
ABDC=GHEF. Find the measure of

Answers
Answer:
b
Step-by-step explanation:
since ABDC is congruent to GHEF , then corresponding angles in the 2 figures are congruent , that is
∠ D = ∠ E = 80°
I'm having trouble with this assignment, more will be posted

Answers
Answer:
the answer is (b.)
Step-by-step explanation:
hope this helps <3 :))
xx
3. A flat screen television has a diagonal length of 40 inches. The base is 36
inches across. What is the height of the television? Round your answer
to the nearest tenth.
Answers
Answer:
Step-by-step explanation:
43
A rectangular balcony has an area of 28 square meters. Its perimeter is 22 meters. What are the
dimensions of the balcony?
A) 7 meters by 4 meters
B) 14 meters by 2 meters
C) 11 meters by 2 meters
D) 10 meters by 1 meter

Answers
EXPLANATION:
We know that the area of the rectangular balcony is 28 square meters, so lets check if our dimensions match the area:
7 meters • 4 meters = 28 square meters (correct)
So lets check the perimeter: 2 (l + w)
2 ( 7 + 4 ) = 22 meters
HOPE THIS HELPS
-SpaceMarsh