Mikaila is saving money to purchase a laptop computer. She already hassaved $150 in her savings account. Next week Mikaila will begin a tutoringjob that pays $10 per hour. All the money she earns tutoring will be added toher savings account.A. What is the total amount of money Mikaila will have saved in her accountafter tutoring for 12 hours? Show or explain how you got your answer.B. Write an expression to represent the total amount of money Mikaila willhave saved in her account after tutoring for x hours.C. The least expensive laptop that Mikaila is considering purchasing costs$550, including tax.Write and solve an inequality to determine the minimum number of hoursMikaila needs to tutor to have enough money in her savings account topurchase a laptop that costs $550 or more. Show or explain how you gotyour answer.D. The most expensive laptop that Mikaila is considering purchasing costs$1,150, including tax.Write and solve a compound inequality to determine the number of hoursMikaila needs to tutor to have enough money in her savings account topurchase a laptop that costs at least $550 but not more than $1,150.Show or explain how you got your answer.
Answers
Given:
Amount of money previously saved = $ 150.
Amount of money saved from tutoring job per hour = $ 10.
Required:
( a ) Total amount of money saved after tutoring for 12 hours.
( b ) expression to represent the total amount of money Mikaila saved after working for x hours.
( c ) Inequality to determine the minimum number of hours.
( d ) Compound inequality to determine the number of hours Mikaila needs to tutor to have enough money in her savings account to purchase a laptop that costs at least $550 but not more than $1,1550.
Explanation:
( a ) Amount of money saved after tutoring for 12 hours is calculated as,
\(Money\text{ saved due to tutoring = 12 }\times\text{ 10 = \$ 120}\)Total amount of money saved = $ 150 + $ 120 = $ 270
Thus the total amount of money saved after tutoring for 12 hours is $ 270.
( b ) The amount of money saved after tutoring for x hours is calculated as,
\(After\text{ x hours of tutoring = 10x}\)Total amount of money saved after x hours = 10x + $ 150.
Thus the total amount of money saved after tutoring for x hours is 10x + $ 150.
( c ) The required inequality is calculated as,
\(Inequality\text{ = 10x + 150 }\ge\text{ 550}\)Inequality representing the minimum number of hours required to purchase a laptop for $ 150 or more is calculated as,
\(\begin{gathered} 10x\text{ + 150 }\ge\text{ 550 } \\ 10x\text{ + 150 - 150 }\ge\text{ 550 - 150} \\ 10x\text{ }\ge\text{ 400} \\ x\text{ }\ge\text{ 40} \end{gathered}\)( d ) In inequality represents the number of hours Mikaila needs to work to purchase a laptop that costs more than or equal to $ 150 and less than or equal to $ 1150 is calculated as,
\(\begin{gathered} 1150\ge10x\text{ + 150}\ge550 \\ \end{gathered}\)On solving,
\(\begin{gathered} 1150\text{ }\ge\text{ 10x + 150} \\ 1150\text{ - 150 }\ge\text{ 10x + 150 - 150} \\ 1000\text{ }\ge\text{ 10x } \\ 100\ge x \\ x\text{ }\leq\text{ 100} \end{gathered}\)Further,
\(\begin{gathered} 10x\text{ + 150 }\ge\text{ 550} \\ 10x\text{ + 150 - 150 }\ge\text{ 550 - 150} \\ 10x\text{ }\ge\text{ 400} \\ x\text{ }\ge\text{ 40} \end{gathered}\)Thus the required inequality representing the number of hours is
\(40\leq x\leq100\)Answer:
(a) Total amount of money saved after tutoring for 12 hours is $ 270.
(b) Expression to represent the total amount of money Mikaila saved after working for x hours is 10x + $ 150.
(c) Inequality to determine the minimum number of hours for purchasing the laptop for $ 550 or more.
\(x\ge40\)(d) Compound inequality to determine the number of hours Mikaila needs to tutor to have enough money in her savings account to purchase a laptop that costs at least $550 but not more than $1,1550 is,
\(40\leq x\leq100\)
Related Questions
Can anyone help me with this Algebra?

Answers
The function's minimum value is -1, and as x moves away from the vertex in either direction, it gets smaller.
What is the name of a quadratic function?If a polynomial function has one or more variables and a variable with a maximum exponent of two, it is said to be quadratic. It is frequently referred to as the polynomial of degree 2 since the second-degree term in a quadratic function has the highest degree.
The graph displays a quadratic function with a downward opening (a negative leading coefficient). The minimal point of the function, point (2,-1), is where the parabola's vertex is located. The graph's x-intercepts, which are the solutions to the equation f(x) = 0, are (0,4) and (4,0).
The vertical line that passes through the vertex and has the value x = 2 is the parabola's axis of symmetry. As there are no limitations on the input values of x, the function's domain spans the entire real number range. As the function's minimum value is -1, its range is all real values less than or equal to -1. The function decrements as x moves away from the vertex in either direction.
To know more about quadratic function visit:
https://brainly.com/question/18958913
#SPJ1
Use the image to determine the direction and angle of rotation.
graph of triangle ABC in quadrant 4 and a second polygon A prime B prime C prime in quadrant 2
90° clockwise rotation
90° counterclockwise rotation
180° clockwise rotation
270° counterclockwise rotation
Answers
The angle of rotation for the described transformation is
180° clockwise rotationHow to know the angle of rotationThe movement or transformation described is form quadrant 4 to quadrant 2.
The transformation will require 180 degrees transformation.
In this type of transformation, both clockwise and the counter clockwise have similar effects
Learn more about angle of rotation at
https://brainly.com/question/2078551
#SPJ1
The mean weight of an adult is 6565 kilograms with a standard deviation of 1313 kilograms. If 9292 adults are randomly selected, what is the probability that the sample mean would be greater than 62.762.7 kilograms
Answers
Answer: 0.9554
Step-by-step explanation:
Let \(\overline{X}\) be the sample mean.
Given: Mean weight\((\mu)\) of an adult is 65 kilograms with a standard deviation\((\sigma)\) of 13 kilograms.
Sample space = 92
The probability that the sample mean would be greater than 62.7 kilograms:
\(P(\overline{X}>62.7)=P(\dfrac{\overline{X}-\mu}{\dfrac{\sigma}{\sqrt{n}}}>\dfrac{62.7-65}{\dfrac{13}{\sqrt{92}}})\\\\=P(Z>-1.70)\\\\=P(Z<1.70)\ \ \ \[P(Z>-z)=P(Z<z)]\\\\=0.9554\)[ By p-value table]
Hence, the required probability= 0.9554
Which statement describes the graph of y + 2 ≥ –4(x – 3)2? a parabola opening up, with shading above the vertex a parabola opening up, with shading below the vertex a parabola opening down, with shading above the vertex a parabola opening down, with shading below the vertex
Answers
Option C. The statement that describes the graph of the equation y + 2 ≥ –4(x – 3)2 is a a parabola opening down, with shading above the vertex.
How to describe the shape of the parabola.To do this you have to create a graph of the equation as seen in the attachment.
From the attachment we can see that the parabola is shaped downwards while we have the shading to be at the top of the vertex.
Read more on parabola here:
https://brainly.com/question/22772615
#SPJ1

Draw u – v + w. (4 points)
Answers
The graph of U + V + W vectors is attached accordingly.
What is a vector in math?A vector is a number or phenomena with two distinct properties: magnitude and direction. The word can also refer to a quantity's mathematical or geometrical representation.
From the question,
U = (1,5), iV = (-3, 1) and W = (4, -3)
Thus, U + V + W = (1-3+4, 5+1-3)
= (2, 3)
Hence, the attached graph.
Note that In nature, vectors include velocity, momentum, force, electromagnetic fields, and weight.
Learn more about vectors;
https://brainly.com/question/25705666
#SPJ1


what is tessellation in maths
Answers
Answer: A tiling of regular polygons (in two dimensions), polyhedra (three dimensions), or polytopes ( dimensions) is called a tessellation. Tessellations can be specified using a Schläfli symbol. The breaking up of self-intersecting polygons into simple polygons is also called tessellation.
Hope this helps!
ashey, Frank, and erick have a total of $86 in their wallets. Ashey has $6 more than Erick. Frank has 2 times what Erick has. How much does each have?amount in asheys wallet= amount in franks wallet =amount in erick wallet =
Answers
"Ashley, Frank, and Erick have a total of $86", this can be expressed as
\(A+F+E=86\)"Ashely has $6 more than Erick", this can be expressed as
\(A=E+6\)"Frank has 2 times what Erick has", this can be expressed as
\(F=2E\)Then, we combine all three equations
\(\begin{gathered} A+F+E=86 \\ E+6+2E+E=86 \end{gathered}\)Let's solve for E.
\(\begin{gathered} 4E+6=86 \\ 4E=86-6 \\ E=\frac{80}{4}_{}_{} \\ E=20 \end{gathered}\)Erick has $20.Then, we find the other values.
\(\begin{gathered} A=E+6=20+6=26 \\ F=2E=2\cdot20=40 \end{gathered}\)Ashley has $26.Frank has $40.A number rounded to the nearest thousand is 47,000 which number could be the number that was rounded
Answers
Answer:
Anything greater than or equal to 46,500, and less than or equal to 47,499 could be the answer.
For example, a number, let's say 46,589 falls within that range and may have been the number that was rounded.
need help asap pic 48 POINTS

Answers
Answer:
p = -9 ; open circle pointing left
Step-by-step explanation:
-7p + 3 < - 60
*subtract 3 from both sides*
-7p < -63
*divide both sides by -7*
p < -9
You are working as an office apprentice for bksb newcastle arena you are helping collect a customer satisfaction survey for the arena enter the following replies into the table below
Answers
To find the area of the arena, you will need to find the areas of the rectangular spaces and the 2 semicircles. Because the formulas are given, I will just substitute in the values and show the work for finding the areas.
To find the perimeter, you will look at the distances of lines that take you around the space. Because two of these spaces are half circles, you will need to find the circumference of the full circle.
Also, the answers need to be given in meters, so all units given in centimeters will be divided by 100 to convert them to meters.
Perimeter:
C= 3.14 x 20 m
C = 62.8 meters
62.8 + 8 + 25 + 8 + 5 + 8 + 10 + 8 + 40= 174.8 meters for the Perimeter
Area:
A = 25 x 8
A = 200 square meters
A = 10 x 8
A = 80 square meters
A = 20 x 40
A = 800 square meters
A = 3.14 x 10^2
A = 314 square meters
Total Area: 314 + 800 + 80 + 200= 1394 square meters
Question 5What are the factors of4x2 + 20x + 25(2x – 5)²0 (20+5)O (2.c + 5)(2x - 5)(2x + 5)2
Answers
ANSWER
\((2x+5)^2\)EXPLANATION
We want to find the factors of:
\(4x^2\text{ + 20x + 25}\)To do that we simply have to factorise the equation.
That is we need two numbers such that:
their sum = 20
their product = 4 * 25 = 100
The two numbers we need are 10 and 10.
That is:
\(\begin{gathered} \Rightarrow4x^2\text{ + 10x + 10x + 25} \\ \text{Factorise by grouping them:} \\ (4x^2\text{ + 10x) + (10x + 25)} \\ =\text{ 2x(2x + 5) + 5}(2x\text{ + 5)} \\ =\text{ (2x + 5)(2x + 5)} \\ =(2x+5)^2 \end{gathered}\)That is the answer.
Brainliest if correct

Answers
Answer:
9 over 0 = 9/0 also - 9
Step-by-step explanation:
An adult has a total of about 22.9 square feet of skin. Use the fact that 1 meter is approximately equal to 3.281 feet to convert this measurement to square meters
Answers
An adult has a total of about 22.9 square feet of skin . if we use fact that 1 meter is approximately equal to 3.281 feet . Thus 22.9 square feet should be equal to 2.12 meter².
Here, we know that
1 m = 3.281 ft
1 m² = (3.281 ft)² (∵ squaring both the side of equation )
now we are going to convert 22.9 ft² to m²
1 m²= ( 3.281 ft )²
22.9 m² = x ft²
x ft² = 22.9 m²/ (3.281 ft )²
x ft² = 22.9 m²/ 10.7649 ft²
x ft² = 2.12 m²
So, 22.9 square feet is equal to 2.12 meter².
To learn more about other example :
https://brainly.com/question/23740877?referrer=searchResults
please help
please hurry

Answers
The graph of the function is graph (b)
How to determine the graph of the function?The equation of the graph is given as
f(x) = |x - 3|
The above equation is an absolute value function
An absolute value function is represented as
f(x) = a|x - h| + k
Where the vertex is
Vertex = (h, k)
From the given equation, we have
(h, k) = (3, 0)
a = 1
When a is positive, the graph opens up
From the graphs in the options, we have graph (b) that has the following features
(h, k) = (3, 0) and it opens upward
Hence, the graph of the function is graph (b)
Read more about absolute value function at
https://brainly.com/question/3381225
#SPJ1
what is the radius of the cylinder

Answers
Select the correct answer.
Tom gets $12 off a box of chocolates that had an original price of $48. What percentage is the discount?
A. 12%
B. 25%
C. 50%
D. 60%
Answers
Find the average rate of change of g(x) =– 1x - 5 between the points (-4,-1) and (1,-6)
Answers
Answer:
m= -1
Step-by-step explanation:
Which of the following is a point-slope equation for a line with the point (-2,4) and a slope of three
Answers
hope this helps
HELPPP ME ASAP FOR 20 EASY POINTSSSS
The area of a floor in square yards is one-ninth the area of the floor in square feet. Write an equation representing y, the area in square yards, to f, the area in square feet.
HELP ME
Answers
Answer:
y = f/9
Step-by-step explanation:
Area of a floor in square yards = y = f/9
Area of a floor in square feet = f
The number that represents the area of the floor in square feet is 9 times the number representing the area in square yards. This makes sense because the ratio of yard to feet is 1 : 3 and the ratio of square yard to square feet is the same ratio but squared so 1 : 9.
If y represents the area in square yards and f the area in square feet.
y = f/9
Faith invested $3,100 in an account paying an interest rate of 4.1% compounded continuously. Assuming no deposits or withdrawals are made, how much money, to the nearest dollar, would be in the account after 15 years?
Answers
Answer:
39000
Step-by-step explanation:
it will be 39000 after 15 years
Enter the number that belongs in the green box
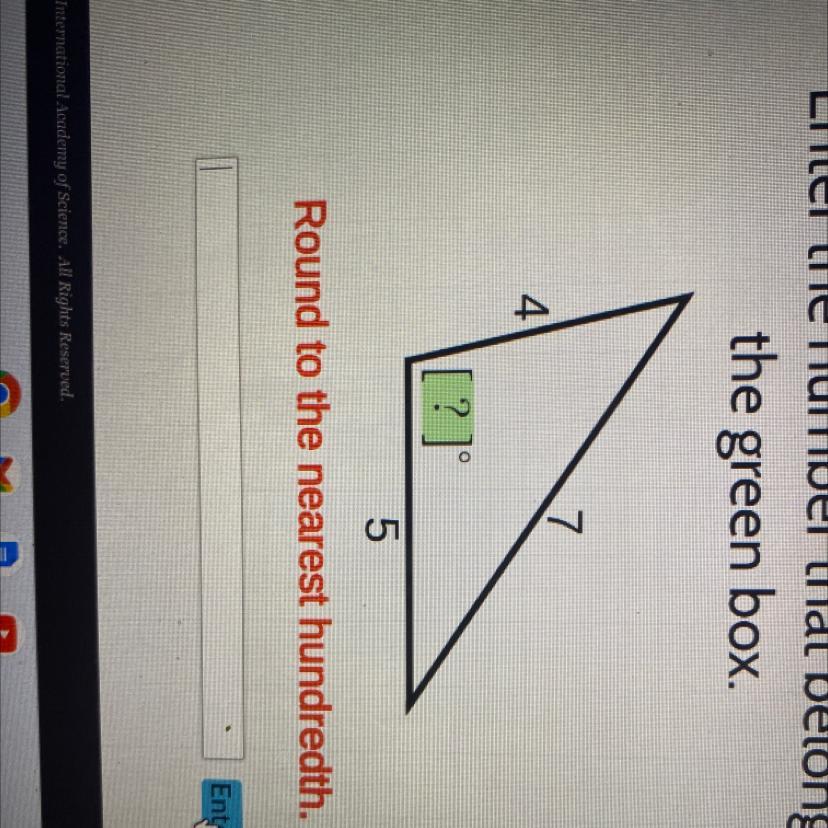
Answers
The angle between the sides measuring 4 and 5 in the obtuse triangle is approximately 101.54 degrees.
To find the measure of the angle between the sides measuring 4 and 5 in an obtuse triangle with side lengths 4, 5, and 7, we can use the Law of Cosines. The Law of Cosines states that in a triangle with side lengths a, b, and c, and an angle opposite to side c, the following equation holds:
\(c^2 = a^2 + b^2 - 2ab*cos(C)\)
In this case, we have side lengths a = 4, b = 5, and c = 7. We want to find the angle C, which is opposite to side c. Substituting these values into the Law of Cosines, we get:
\(7^2 = 4^2 + 5^2\)- 2(4)(5)*cos(C)
49 = 16 + 25 - 40*cos(C)
49 = 41 - 40*cos(C)
40*cos(C) = 41 - 49
40*cos(C) = -8
cos(C) = -8/40
cos(C) = -0.2
To find the measure of angle C, we can take the inverse cosine (arccos) of -0.2:
C = arccos(-0.2)
Using a calculator, we find that C ≈ 101.54 degrees.
Therefore, the measure of the angle between the sides measuring 4 and 5 in the obtuse triangle is approximately 101.54 degrees.
For more such information on: angle
https://brainly.com/question/25716982
#SPJ8
Find the distance between the pair of points.
(0, -7) and (-3, -7)
Answers
Answer:
\(d =3\)
General Formulas and Concepts:
Pre-Alg
Order of Operations: BPEMDASAlgebra II
Distance Formula: \(d = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)Step-by-step explanation:
Step 1: Define
Point (0, -7)
Point (-3, -7)
Step 2: Find distance d
Substitute: \(d = \sqrt{(-3-0)^2+(-7+7)^2}\)Subtract/Add: \(d = \sqrt{(-3)^2+(0)^2}\)Evaluate: \(d = \sqrt{9}\)Evaluate: \(d =3\)I NEED HELP ASAP PLEASE GEOMETRY

Answers
Answer:
100°
Step-by-step explanation:
The sum of all the angles of a kite is 360°.
So:
360-(124+36)
=200
∠s = 200/2
=100°
Hope this helped lol
01:37:35
What is the difference between the largest prime number less than 50 and the smallest composite number greater than 10
Answers
Answer:
35
Step-by-step explanation:
47-12=35
the half-life of radium-226 is about 1,590 years. How much of a 100mg sample will be left in 500 years
Answers
Aa Bb Cc Dd Ee Ff Gg Hh Ii Jj Kk Ll Mm Nn Oo Pp Qq Rr Ss Tt Uu Vv Ww Xx Yy Zz
I know the best answer ever (*says sarcastically*)
points A and B are shown on a coordinate plane
point A is at (-8, 6) point B is at (-2, -2)
What is the length of AB and the coordinates of its midpoint?
AB= __ units
the midpoint of AB is (_,_)

Answers
The length of AB would be = 10 units and the midpoint of segment AB would be (-5, 2).
What are the distance formula and midpoint of a segment?
The distance formula is a mathematical formula that can be used to determine the distance between two points in a coordinate plane. The distance between two points (x1, y1) and (x2, y2) is given by the formula:
\(d = \sqrt{(x2 - x1)^2 + (y2 - y1)^2}\)
The midpoint of a segment is a point that is exactly in the middle of a line segment. Given the endpoints of the line segment, (x1, y1) and (x2, y2) the coordinates of the midpoint, (x, y) can be calculated using the following formulas:
x = (x1 + x2) / 2
y = (y1 + y2) / 2
The given points are (-8, 6) and (-2, -2).
Given two points A(x1, y1) = (-8, 6) and B(x2, y2) = (-2, -2), we can use the distance formula to find the length of the line segment AB. The distance formula is:
\(d = \sqrt{(x2 - x1)^2 + (y2 - y1)^2}\\\\d= \sqrt{((-2) - (-8))^2 + ((-2) - (6))^2}\\\\d=\sqrt{36 + 64}\\\\d=\sqrt{100}\\\\d=10\)
The length of AB would be 10.
To find the coordinates of the midpoint of AB, we can use the midpoint formula:
x = (x1 + x2) / 2
y = (y1 + y2) / 2
Plugging in the values for A and B, we get:
x = (-8 + (-2)) / 2 = -5
y = (6 + (-2)) / 2 = 2
The coordinates of the midpoint of AB are (-5, 2).
Hence, the length of AB would be = 10 units and the midpoint of segment AB would be (-5, 2).
To learn more about the distance formula and midpoint of a segment, visit:
https://brainly.com/question/28778717
#SPJ1
9. Which statements contradict each other? I. triangle ABC is a right triangle. II. m angle A = 41° III. m angle B = 103° A. I and II B. I and III C. II and III D. None of the statements are contradictory. 1
Answers
The contradicting statement is
B. I and III
How to know the contradictory statementThe contradictory statement is that of I and III since the sum of angles in a triangle is always 180 degrees.
Given that
I. triangle ABC is a right triangle. say angle C = 90 degrees and
angle B = 103 degrees,
So the sum of the angles in the triangle would be:
= angle B + m angle C
= 103 + 91
= 194
This is against the law of angles of a triangle
Learn more about angles in a triangle at
https://brainly.com/question/25215131
#SPJ1
Area of the base, B = 42 square meters
and height = 3 meters
Answers
Answer:
14
Step-by-step explanation:
all i did was divided 42 by 3 and got 14
Help, please
f(n)=3(n+2)^2 (n-3) (n-2)
As n -----> -oo, f(n)----> ?
As n ----->oo, f(n) ----->?
Answers
The end behavior of the function f(n) = 3(n + 2)²(n - 3)(n - 2) is given as follows:
As n -> -oo, f(n) -> oo.As n -> oo, f(n) -> +oo.What is the end behavior of a function?The end behavior of a function refers to how the function behaves as the input variable approaches positive or negative infinity.
The function for this problem is given as follows:
f(n) = 3(n + 2)²(n - 3)(n - 2).
Considering the degree, the function can be interpreted as follows:
\(3n^4\)
(for the limit when the input goes to infinity we consider only the term with the highest degree).
The leading coefficient is positive and the exponent is even, hence the end behavior is given as follows:
As n -> -oo, f(n) -> oo.As n -> oo, f(n) -> +oo.More can be learned about the end behavior of a function at brainly.com/question/1365136
#SPJ1
Consider purchasing a system of audio components consisting of a receiver, a pair of speakers, and a CD player. Let A1 be the event that the receiver functions properly throughout the warranty period, A2 be the event that the speakers function properly throughout the warranty period, and A3 be the event that the CD player functions properly throughout the warranty period. Suppose that these events are (mutually) independent with P(A1)= .95, P(A2) = .98, and P(A3) = .80.a. What is the probability that all three components function properly throughout the warranty period?b. What is the probability that at least one component needs service during the warranty period?c. What is the probability that all three components need service during the warranty period?
Answers
Answer:
that is alot the prob. is 20
Step-by-step explanation: