Answers
Answer:
A 20°
Step-by-step explanation:
Explanation:-
Given graph
The corresponding angles are congruent (equal to each other)
(x+60)° = 4 x°
x + 60 = 4x
4x-x = 60
3x =60
x = 20°
The value of x=20°
Related Questions
Help ..
Find the volume of the composite figure shown.
Please only answer if u know

Answers
Answer:
64
Step-by-step explanation:
split it in half den it is two rectangles and they are both 32 so 32 * 2 is 64
50 POINTS AND BRAINILEST!!!!!!!!!!!!!!!!
Stanley runs, swims, and bikes every day. During these workouts, he runs at 9 mph, bikes at 16 mph, swims at 2.5 mph. Yesterday, he ran for half an hour longer than he swan, and his biking time was twice his running time. How long did Stanley run, swim, and bike yesterday if the total distance he covered was 64 miles. What distance did Stanley cover while swimming?
Answers
Answer: 3x-x+2=4
Step-by-step explanation:
You can put this solution on YOUR website!
running distance is 9(t3+0.5)
biking distance is 16 (2(t3+0.5))=16(2t3+1)
swimming distance is 2.5t3
9t3+4.5+32t3+16+2.5t3=64
43.5t3=43.5
t3=1 hour
He biked for 3 hours (48 miles)
He ran for 1.5 hours (13.5 miles)
He swam for 1 hour (2.5 miles)
He covered 62 miles in 5.5 hours of activity.
Answer:
He swam for 1 hour (2.5 miles)
Step-by-step explanation:
The relation between time, speed, and distance is,
distance = speed × time
write y-5=(4/3)(x-6) into a point intercept form
Answers
The equation y - 5 = (4/3)(x - 6) can be written in point-intercept form as y = (4/3)x - 3, where the slope is 4/3 and the y-intercept is -3.
The point-slope form of a line is y - y1 = m(x - x1), where m is the slope and (x1, y1) is a point on the line. The point-slope form of a line can be converted to the slope-intercept form of a line, y = mx + b, where b is the y-intercept.
The equation y - 5 = (4/3)(x - 6) can be rearranged into the point-slope form of a line by isolating the y-term and simplifying: y - 5 = (4/3)(x - 6)y - 5 = (4/3)x - 8y = (4/3)x - 3
Now, we have the point-slope form of the line with slope 4/3 and y-intercept -3.
To convert this to the slope-intercept form of a line, we simply rearrange the equation to solve for y:y = (4/3)x - 3 This is the slope-intercept form of the line, where the slope is 4/3 and the y-intercept is -3.
Thus, the equation y - 5 = (4/3)(x - 6) can be written in point-intercept form as y = (4/3)x - 3, where the slope is 4/3 and the y-intercept is -3.
For more such questions on point-intercept
https://brainly.com/question/10517354
#SPJ8
King of Diamonds Industries has bonds on the market making annual payments, with 14 years to maturity, and selling for R1 482,01. At this price, the bonds yield 7%. What is the coupon rate?
Answers
The coupon rate of the bonds by King of Diamonds Industries would be 7 %.
How to find the coupon rate ?The formula for the bond price shows the coupon payment and so can be used to find the coupon rate:
= (Coupon payment x ( 1 - ( 1 + r ) ^ ( - number of years till maturity ) ) ) / r + Face value / (1 + rate )^ number of years
1,482.01 = (C x (1 - (1 + 0.07 )^ (- 14) ) ) / 0.07 + F / (1 + 0.07 ) ^ 14
103.7407 - 0.07 x (F / (1 + 0.07) ^14 ) = C x (1 - ( 1 + 0.07) ^ ( - 14) )
Using a calculator, C is $ 70.
This means that the coupon rate is:
= 70 / 1, 000
= 7 %
Find out more on the coupon rate at https://brainly.com/question/28528712
#SPJ1
Find domain Range Y-intercept X- intercept Vertical asymptote Horizontal asymptote Pic attached below note write domain and range in interval notation
Find domain
Range
Y-intercept
Xi intercept
Vertical asymptote
Horizontal asymptote
Pic attached below

Answers
The domain and range of the function f(x) = 3/x + 2 are (-∞, 0) ∪ (0, ∞) and (-∞, 2) ∪ (2, ∞). The vertical and horizontal asymptotes are x = 0 and y = 2 respectively
What is the domain and range of a functionIn mathematics, the domain of a function is the set of all possible input values (also known as the independent variable) for which the function is defined. The range of a function is the set of all possible output values (also known as the dependent variable) that the function can produce.
To determine the domain and range of a function, it's important to consider the nature of the function, its graph or formula, and any restrictions that may apply.
The function f(x) = 3/x + 2
The domain of the function is (-∞, 0) ∪ (0, ∞)
The range of the function is (-∞, 2) ∪ (2, ∞)
The x - intercept is (-3/2, 0)
The y - intercept does not exist
The vertical asymptotes is x = 0
The horizontal asymptotes is y = 2
Learn more on domain and range of a function here;
https://brainly.com/question/10197594
#SPJ1
How many different ID cards can be made if there are eight digits on a card if digits can be repeated?
Answers
Answer:
Step-by-step explanation:
10^8 cards
PLEASE HELP ME!
Which is a solution of the inequality x + 2 <8?
Group of answer choices
z < 4
z < 6
z = 6
z < 10
Answers
Answer:
x < 6
Step-by-step explanation:
\(x+2 < 8\quad :\quad \begin{bmatrix}\mathrm{Solution:}\:&\:x < 6\:\\ \:\mathrm{Interval\:Notation:}&\:\left(-\infty \:,\:6\right)\end{bmatrix}\)
\(\mathrm{Subtract\:}2\mathrm{\:from\:both\:sides}\)
\(x+2-2 < 8-2\)
\(\mathrm{Simplify}\)
\(x < 6\)
~Learn with Lenvy~
Answer:
z < 6
Step-by-step explanation:
this is the correct answer
Determine the smallest integer value of x in the solution of the following inequality.
-3x+10≤5
Answers
Answer: The smallest integer value of x in the solution is 1.
Step-by-step explanation:
The given inequality: \(-3x+10\leq5\)
To solve the inequality, we first subtract 10 from both sides
\(-3x+10-10\leq5-10\\\\\Rightarrow\ -3x\leq-5\)
Multiply negative sign on both sides ,we get
\(3x\geq5\)
Divide both sides by 3, we get
\(x\geq\frac{5}{3}\)
i.e. \(x\geq 1.6666666667\\\)
\(x\geq1\)
Hence, the smallest integer value of x in the solution is 1.
A bag contains 4 red marbles, 6 blue marbles, and 7 green marbles. What is the probability of choosing a blue marble when one marble is drawn?
Answers
Answer:
Probabilty of selecting a blue marble if one marble is drawn
= 0.3529
Step-by-step explanation:
A bag contains 4 red marbles, 6 blue marbles, and 7 green marble.
Total number of marbles
=4 red+ 6 blue+7 green
= 17 marbles in total
Probabilty of selecting a blue marble if one marble is drawn
= Number of blue marble/total number of marble
Probabilty of selecting a blue marble if one marble is drawn
= 6/17
Probabilty of selecting a blue marble if one marble is drawn
= 0.3529
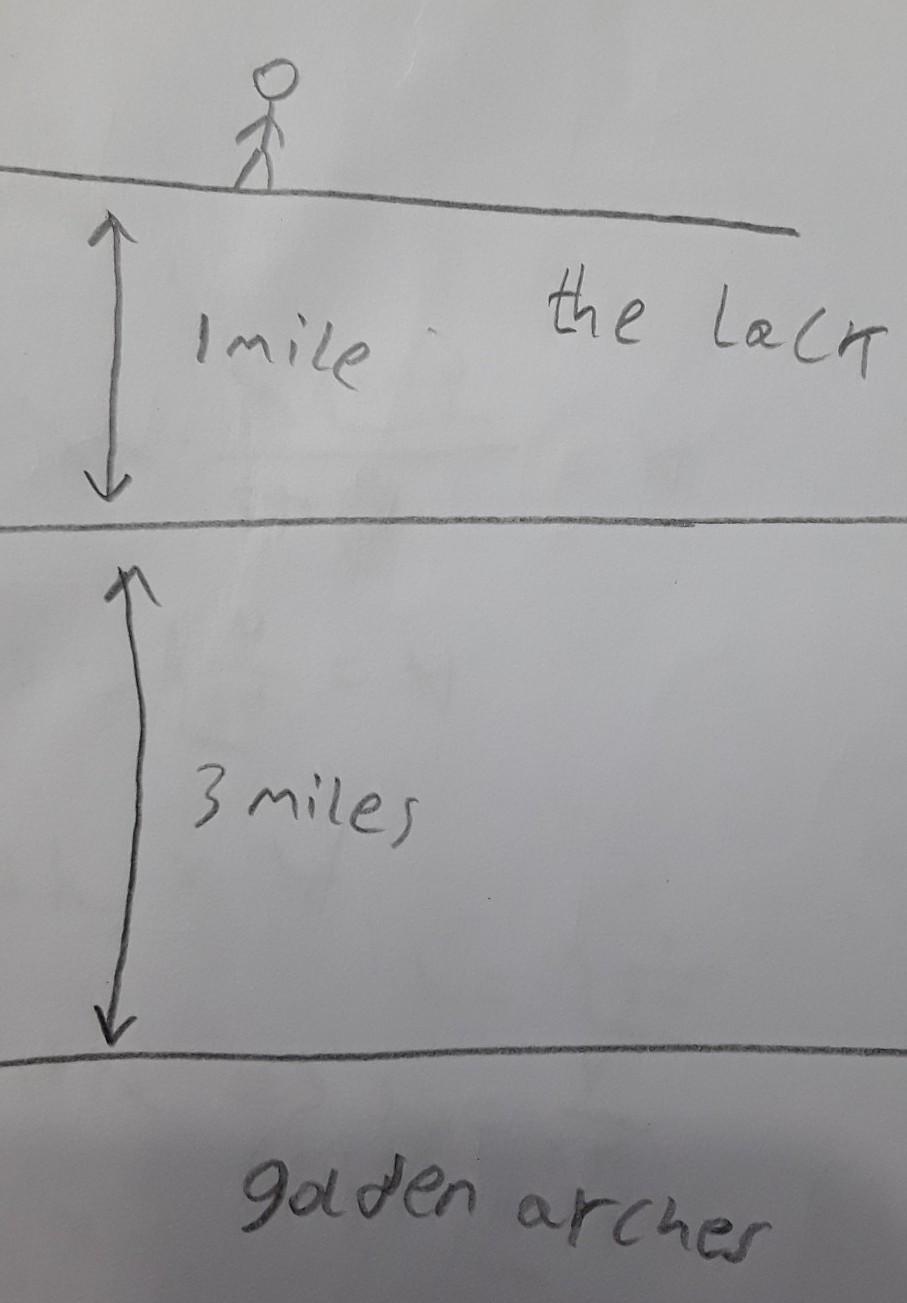
A boy standing on the shore of a lake 1 mile wide wants to reach the “Golden Arches” 3 miles down the shore on the opposite of the lake. If he swims at 2 mph and walks at 4 mph, is it quicker for him to swim directly across the lake and then walk to the Golden Arches or to swim directly to the Golden Arches? To the nearest minute, how much quicker?
Answers
Answer:
it is a matter of time
the speed is constant
use v=d/t
to find t and comparing it
Step-by-step explanation:
and in the 2nd case assume a cannel directly conects the land that boy stands on and the golden arches with the same distances
and note that the units are the same
The table represents a linear relationship
X—2 0 4
Y-4 3 1
Which equation represents the table
Y=1/2x+5
y=-1/2x+3
Y=2x-3
Y=-4x+2
Answers
The linear relationship illustrated in the provided table can be effectively described by the equation Y = -4x + 2. Option D.
To determine the equation that represents the given table with the values of x and y, we can observe the pattern and find the equation of the line that fits these points.
Given the table:
X: 2 0 4
Y: -4 3 1
We can plot these points on a graph and see that they form a straight line.
Plotting the points (2, -4), (0, 3), and (4, 1), we can see that they lie on a line that has a negative slope.
Based on the given options, we can now evaluate each equation to see which one represents the line:
Y = 1/2x + 5
When we substitute the x-values from the table into this equation, we get the following corresponding y-values: -3, 5, and 6. These values do not match the given table, so this equation does not represent the table.
Y = -1/2x + 3
When we substitute the x-values from the table into this equation, we get the corresponding y-values: 4, 3, and 2. These values also do not match the given table, so this equation does not represent the table.
Y = 2x - 3
When we substitute the x-values from the table into this equation, we get the corresponding y-values: -4, -3, and 5. These values do not match the given table, so this equation does not represent the table.
Y = -4x + 2
When we substitute the x-values from the table into this equation, we get the corresponding y-values: -6, 2, and -14. Interestingly, these values match the y-values in the given table. Therefore, the equation Y = -4x + 2 represents the table.
In conclusion, the equation Y = -4x + 2 represents the linear relationship described by the given table. So Option D is correct.
For more question on equation visit:
https://brainly.com/question/29174899
#SPJ8
Two investment portfolios are shown with the amount of money placed in each investment
and the ROR.
Investment
Tech Company Stock $2,800
Government Bond
$3,200
$950
$1,500
Junk Bond
Portfolio 1 Portfolio 2
Common Stock
O Portfolio 1 earns $31.77 more.
I
O Portfolio 2 earns $31.77 more.
O Portfolio 1 earns $69.17 more.
$1,275
$2,200
$865
$1,700
Which portfolio earns the most, and by how much?
Cortfolio 2 earns $69.17 more.
ROR
4.63%
-1.87%
2.50%
11.13%
Answers
Portfolio 1 earns $31.77 more than portfolio 2.
To compare the two portfolios, we need to calculate the rate of return (ROR) for each one. To do so, we can use the following formula:
ROR = (gain or loss / initial investment) x 100%
Let's calculate the ROR for each investment in portfolio 1:
Tech Company Stock: 4.63%
Government Bond: -1.87%
Junk Bond: 2.50%
Common Stock: 11.13%
To calculate the overall ROR for portfolio 1, we need to weight each investment by the amount invested. The total initial investment for portfolio 1 is:
= $2,800 + $3,200 + $950 + $1,500
= $8,450
The weighted average ROR for portfolio 1 is:
= (0.463 x $2,800 + (-0.0187) x $3,200 + 0.025 x $950 + 0.1113 x $1,500) / $8,450 x 100%
= 3.12%
Now let's do the same for portfolio 2:
Tech Company Stock: 2.50%
Government Bond: 11.13%
Junk Bond: 4.63%
Common Stock: -1.87%
The total initial investment for portfolio 2 is:
= $1,275 + $2,200 + $865 + $1,700
= $6,040
The weighted average ROR for portfolio 2 is:
= (0.025 x $1,275 + 0.1113 x $2,200 + 0.0463 x $865 + (-0.0187) x $1,700) / $6,040 x 100%
= 3.03%
Therefore, portfolio 1 earns $31.77 more than portfolio 2.
Learn more about Investment Plan here:
https://brainly.com/question/31781807
#SPJ1
1. How much money would the restaurant take in by selling 100 burritos? (2 points)
Answers
Answer:
Multiply price of each burrito by 100
Step-by-step explanation:
WILL GIVE BRAINLYEST
Make an inequality in standard fom with two variables and explain a real world
Situation that may apply.
Explain how you would graph the inequality
Answers
Answer:
The graph of an inequality in two variables is the set of points that represents all solutions to the inequality. A linear inequality divides the coordinate plane into two halves by a boundary line where one half represents the solutions of the inequality. The boundary line is dashed for > and < and solid for ≤ and ≥.
Step-by-step explanation:
Question 12 The GPAs of all students enrolled at a large university have an approximately normal distribution with a mean of and a standard deviation of . Find the probability that the mean GPA of a random sample of students selected from this university is or higher.
Answers
Complete question :
The GPAs of all students enrolled at a large university have an approximately normal distribution with a mean of 3.02 and a standard deviation of .29.Find the probability that the mean GPA of a random sample of 20 students selected from this university is 3.10 or higher.
Answer:
0.10868
Step-by-step explanation:
Given that :
Mean (m) = 3.02
Standard deviation (s) = 0.29
Sample size (n) = 20
Probability of 3.10 GPA or higher
P(x ≥ 3.10)
Applying the relation to obtain the standardized score (Z) :
Z = (x - m) / s /√n
Z = (3.10 - 3.02) / 0.29 / √20
Z = 0.08 / 0.0648459
Z = 1.2336940
p(Z ≥ 1.2336) = 0.10868 ( Z probability calculator)
Write an equation in slope-intercept form of the line that passes through the points (1, 2) and (-2, -1)
y=
Answers
Answer:
y=x+1
Step-by-step explanation:
Firstly, we need to know that the slope intercept form is known as:
y=mx+b, where y and x are coordinates, m is the slope and b is the y intercept.
We need to find m first, and then b. By doing that, we use the formula:
\(\frac{y1-y2}{x1-x2} \\\\\\y1=2\\y2=-1\\x1=1\\x2=-2\)
Plugging those values in, we get:
\(m= \frac{2-(-1)}{1-(-2)} \\\\= \frac{3}{3} \\=1\)
So with this information, we already know that y=1x+b. We just need to find b.
So we can pick one of the two coordinates given. Let's use (1,2) and plug those in.
2=1(1)+b
Now with that, we solve for b.
2=1+b
2-1=b
1=b
b=1
Therefore, we have the final equation of y=1x+1
or better,
y=x+1
(One penny measures 0.75 inches in length.) If we lined up these 288 billion pennies, how long (in billions of inches) would the line be?
Answers
Answer:
216,000,000,000 inches
Step-by-step explanation:
4. Which expression is equivalent to the given expression? 1 (6x + 9) - 2 x ma
Answers
we have the expression
\(-\frac{1}{2}(6x+9)-(x-\frac{3}{2})\)step 1
Apply distributive property first term
\(\begin{gathered} -\frac{1}{2}(6x)-\frac{1}{2}(9)-(x-\frac{3}{2}) \\ -3x-\frac{9}{2}-(x-\frac{3}{2}) \end{gathered}\)step 2
Remove the parenthesis
\(-3x-\frac{9}{2}-x+\frac{3}{2}\)step 3
Combine like terms
\(\begin{gathered} -4x-\frac{6}{2} \\ -4x-3 \end{gathered}\)The owners of a baseball team are building a new baseball field for their team and must determine the number of seats to include. The average game is attended by 6,500 fans, with a standard deviation of 450 people. Suppose a random sample of 35 games is selected to help the owners decide the number of seats to include. Identify each of the following and be sure to round to the nearest whole number:
Provide your answer below:
μ =------------
μx=-----------
σx=-----------
σ=------------
n=------------
Answers
Answer:
μ = 6500
μx= 6500
σx= 76
σ= 450
n= 35
Step-by-step explanation:
Central Limit Theorem
The Central Limit Theorem establishes that, for a normally distributed random variable X, with mean \(\mu\) and standard deviation \(\sigma\), the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean \(\mu\) and standard deviation \(s = \frac{\sigma}{\sqrt{n}}\).
For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.
The average game is attended by 6,500 fans, with a standard deviation of 450 people.
This means that \(\mu = 6500, \sigma = 450\)
35 games:
This means that \(n = 35\)
Distribution of the sample mean:
By the Central Limit Theorem, we have \(\mu_x = \mu = 6500\) and the standard deviation is:
\(\sigma_x = \frac{450}{\sqrt{35}} = 76\)
each plant in Johns garden has either 5 leaves or 2 leaves and 1 flower. In total, tge plants hace 6 flowers and 32 leaves. How many plants are there?
Answers
Answer:
5x
Step-by-step explanation:
Let's assume that the number of plants with 5 leaves is x, and the number of plants with 2 leaves and 1 flower is y. Then, we can write two equations based on the information given:
x + y = 6 (total number of flowers)
5x + 2y = 32 (total number of leaves)
To solve for x and y, we can use the substitution or elimination method. Let's use the substitution method here.
From the first equation, we get:
y = 6 - x
Substituting this into the second equation, we get:
5x + 2(6 - x) = 32
5x + 12 - 2x = 32
3x = 20
x = 20/3
This means there are approximately 6.67 plants with 5 leaves. To find the number of plants with 2 leaves and 1 flower, we can substitute x back into the first equation:
6.67 + y = 6
y = 6 - 6.67
y = -0.67
This doesn't make sense since we can't have a negative number of plants. Therefore, we made a mistake somewhere. Let's check our equations again.
x + y = 6 (total number of flowers)
5x + 2y = 32 (total number of leaves)
We notice that the second equation should be:
2x + y = 32 (total number of leaves)
Let's use this equation instead:
x + y = 6 (total number of flowers)
2x + y = 32 (total number of leaves)
From the first equation, we get:
y = 6 - x
Substituting this into the second equation, we get:
2x + 6 - x = 32
x = 26
This means there are 26 plants with 5 leaves. To find the number of plants with 2 leaves and 1 flower, we can substitute x back into the first equation:
26 + y = 6
y = 6 - 26
y = -20
Again, this doesn't make sense. We made another mistake somewhere. Let's check our equations again.
x + y = 6 (total number of flowers)
2x + y = 32 (total number of leaves)
We notice that the first equation should be:
2x + y = 6 (total number of flowers)
Let's use these corrected equations:
2x + y = 6 (total number of flowers)
2x + 3y = 32 (total number of leaves)
From the first equation, we get:
y = 6 - 2x
Substituting this into the second equation, we get:
2x + 3(6 - 2x) = 32
2x + 18 - 6x = 32
-4x = 14
x = -14/4
Once again, we get a negative number of plants, which doesn't make sense. Let's check our equations again.
2x + y = 6 (total number of flowers)
2x + 3y = 32 (total number of leaves)
We notice that the first equation should be:
x + y = 6 (total number of flowers)
Let's use these corrected equations:
x + y = 6 (total number of flowers)
5x + 2y = 32 (total number of leaves)
From the first equation, we get:
y = 6 - x
Substituting this into the second equation, we get:
5x
evaluate the function to find three points f(0)=

Answers
Answer:
f(0) = 0
Step-by-step explanation:
f(x) = -sqrt(x)
Let x= 0
f(0) = -sqrt(0)
f(0) = 0
Value of the given function \(f(x) = -\sqrt{x}\) for \(f(0) = 0.\)
What is function?" A function is defined as the relation between the given variable represents set of all input value should have one output each."
According to the question,
Given function,
\(f(x) = -\sqrt{x}\)
Substitute the different values for 'x' for the given function we get,
\(x=1 , f(1) = -\sqrt{1}\)
\(=-1\)
\(x=4 , f(4) = -\sqrt{4}\)
\(=-2\)
\(x=0, f(0) = -\sqrt{0}\)
\(=0\)
Therefore, given relation is a function.
Hence, value of the given function \(f(x) = -\sqrt{x}\) for \(f(0) = 0.\)
Learn more about function here
https://brainly.com/question/12431044
#SPJ2
Find the value of X from the photo

Answers

f(x)=2x-8 and g(x)=1/2x+4
compose the two given functions and simplify
Answers
Composing f(x)=2x-8 and g(x)=1/2x+4 results in the identity function, f(g(x)) = x.
How to compose f(x)=2x-8 and g(x)=1/2x+4To compose the two functions, we substitute g(x) into f(x) in place of x:
f(g(x)) = 2(g(x)) - 8
= 2(1/2x + 4) - 8
= x + 8 - 8
= x
Therefore, composing the two functions results in the identity function, f(g(x)) = x.
Learn more about functions at https://brainly.com/question/11624077
#SPJ1
Lincoln, Nebraska lies directly North of Dallas, Texas. Lincoln is at a latitude of 40.5
degrees N and Dallas is at a latitude of 32.5 degree N. Assuming the radius of the
earth is 3.960 miles, how far apart are these cities in miles to the nearest tenth of a
mile?
Answers
Answer:
The angular speed of a point on Earth is
π12
radian per hour. The Equator lies on a circle of radius approximately 4000 miles. Find the linear velocity, in miles per hour, of a point on the Equator.
Step-by-step explanation:
They are 31.68 miles apart.
What is Length of arc?The formula to measure the length of the arc is – Arc Length Formula (if θ is in degrees) s = 2 π r (θ/360°)
Arc Length Formula (if θ is in radians) s = ϴ × r.
given:
r= 3.960 miles
\(\theta_2\) = 40.5 and \(\theta_1\) = 32.5
We know, l = r\(\theta\)
So, Δl = rΔ\(\theta\)
Δl= r ( \(\theta_2\) - \(\theta_1\) )
Δl = 3.96 ( 40.5 - 32.5)
Δl = 3.96 x 8
Δl= 31.68 miles.
Hence, they are 31.68 miles apart.
Learn more about length of arc here:
https://brainly.com/question/16403495
#SPJ2
Find the commission on a $1250 sale with a commission rate of 5%
Answers
Answer:
He will have in total $1312.50
He earns a total of $62.50
Step-by-step explanation:
1250 x 1.05 = 1312.50
1250 x 0.05 = 62.50
Evaluate the function f(x)= x2 – 3x - 5 at the given values of the independent variable and simplify.
a. f(9)
b. f(x+8)
c. f(-x)
Answers
Correct. The expressions that follow f(x) = and y = are the same, so these are two different ways to write the same function: f(x) = 3x2 + 5 and y = 3x2 + 5.
PLease help <3 and please dont give an answer just for points. I need it to be correct


Answers
The solution to the linear equations in three variable are x = 5, y = -11, and z = 3.
What is a linear equation?It is defined as the relation between three variables, if we plot the graph of the linear equation we will get a straight line.
If in the linear equation, one variable is present, then the equation is known as the linear equation in one variable.
It is given that:
The three linear equations:
2x - y + 4z = 33 ..(i)
x + 2y - 3z = -26 ...(ii)
-5x - 3y + 5z = 23 ...(iii)
After solving the above linear equation by elimination method:
From the equation (i):
\(x=\dfrac{33+y-4z}{2}\) ....(iv)
Plug the above value in the equation (ii) and (iii)
\(\rm \dfrac{33+y-4z}{2}+2y-3z=-26\\\\\\\\ -5\cdot \dfrac{33+y-4z}{2}-3y+5z=23\)
After solving the above linear equation in two variables:
y = -11
z = 3
Plug the above values in the equation (iv)
We get the value of x:
x = (33-11-3(4))/2
x = (33-11-12)/2
x = 10/2
x = 5
Thus, the solution to the linear equations in three variable are x = 5, y = -11, and z = 3.
Learn more about the linear equation here:
brainly.com/question/11897796
#SPJ1
Question
What is the slope of this line?
Options:
A. 5
B. -5
C. -1/5
D. 1/5

Answers
Answer:
D. 1/5
Step-by-step explanation:
you go up 1 points and 5 points to the right
Take two points
(0,2)(5,3)\(\\ \sf\longmapsto m=\dfrac{y_2-y_1}{x_2-x_1}\)
\(\\ \sf\longmapsto m=\dfrac{3-2}{5-0}\)
\(\\ \sf\longmapsto m=\dfrac{1}{5}\)
Find the reminder when 3x² + 2x -7 is divided by x - 1
Answers
Answer:
-2
Step-by-step explanation:
When x = 1, 3x² + 2x - 7 = -2.

12. Rachel plans to study 2 hours for her next exam. How might
plotting her grade on the same graph change your answer
to Exercise 11? Explain your reasoning.
Original content Copyright © by Houghton Mifflin Harcourt. Additions and changes to the original com
108
Answers
The graph showing the relationship between the hours Rachel studies and her grade in the exam indicates that the relationship is a function, from which we get;
12. The response to the question of if the relationship between Rachel's exam grade based on the number of hours studied which is yes the relationship is a function remains true, based on Rachel's exam score of 95 if she studies for 2 hours as indicated in the graph in the question, because the input of 2 has only one output of 95
What is a function?A function is a rule, definition or law that maps the element of an input set unto the elements of an output set such that each element in the input is mapped to only one element in the output set.
Please find attached the possible graph in question, obtained from a similar question posted online, created with MS Excel.
The relationship in the graph of the question is a function, as each input is assigned to only one output.
The value of an output based on an input can be obtained either directly from the available dataset or the value can be predicted based on the value of the input variable using a formula.
The data points on the graph of relationship between the hours Rachel studied and the exam grades include the input and output point (2, 95).
The input value of 2 indicates the number of hours Rachel studies and the output value of 95 indicates Rachel's exam grade.
The relationship remains a function because the input value of 2 same as the other input values, produces only one output value (95), which indicates that the relationship is still a function.Part of the question included in an online post are;
Points on the graph of the relationship between the hours of study and Rachel's exam grades are; (1, 70), (2, 95), (3, 75), (5, 80), (6, 81.5), (9, 95), (11.8, 98)
Learn more about functions here:
https://brainly.com/question/20896994
#SPJ1

