Max is building a swimming pool in this backyard B measures the length and width of the pool so that opposite sides are parallel he also measure the diagonals of the pool to make sure that they are congruent how does he know that the measure of each corner is 90
Answers
he know that the angle of each corner is 90º because the two lenghths and the two wides are parallel this means that the figure is a rectangle. so the solution isnumeral A)
Related Questions
In November, Hilary drove 580 miles in her car. The car travelled 33.5 miles for each gallon of petrol used. Petrol cost 1.09 per litre. 1 gallon = 4.55 litres. Work out the cost of the petrol the car used in November.
Answers
Answer:The cost of petrol used in November is £86
Step-by-step explanation:
Here, we are interested in calculating the cost of the petrol the car used in the month of November.
We proceed as follows;
Total miles driven = 580 miles
Now, on a gallon of petrol, the car will travel 33.5 miles
Thus, the amount of gallon of petrol
used for 580 miles will be 580/33.5
Let’s convert this to liters
Since 1 gallon is 4.55 liters, 580/33.5 gallons will be 580/33.5 * 4.55 = 78.78 liters
now the cost of 1 liter is 1.09, the cost of 78.78 will be 78.78 * 1.09 = 85.87
To the nearest pounds, we have the cost as £86.
HELP PLEASE
this is really hard help me

Answers
100 Points! Use the given features to sketch a linear graph. Only looking for an answer to B. Photo attached. Thank you!

Answers
The linear graph for the function having the features has been plotted and attached below.
What is a linear graph?
A graph is a diagram that depicts the relationship or connection between two or more quantities. Linear implies straight. The x and y coordinates of two points are connected by a straight line, or straight graph, to form a linear graph.
We are given that the x - intercept is 7 and the y - intercept is 2.
This means that the two points are (7, 0) and (0, 2).
Using these points, we will plot the linear graph. We know that linear graph is always a straight line. The same is shown in the graph below.
Hence, the graph of the function having particular features has been obtained.
Learn more about linear graph from the given link
https://brainly.com/question/30094272
#SPJ1

expand the exppresion -7(k-3)
Answers
Answer:
-7k+21
Step-by-step explanation:
Answer:
-7k +21
Step-by-step explanation:
-7(k-3)
Distribute
-7*k -7*(-3)
-7k +21
how long of a chain Can Jill make by attaching a 13 3/4 inch chain to a 15 2/4 in chain?
Answers
Answer:
A - 28 5/4
B - 29 1/4
D - 117/4
Step-by-step explanation:
Solve the proportion
8/3 = g/3
Answers
Answer:
g=8
that is
I hope to be helpful
(4x-10) x (3x²)
Find the area of the rectangle
Answers
If the length of the rectangle be (3x+2) units and width (4x+10)units then the area of the rectangle be \($x=-\frac{2}{3}, x=-\frac{5}{2}$$\).
How to find the area of rectangle?The region enclosed by an object's shape is referred to as the area. The area of the shape is the area that the figure or any other two-dimensional geometric shape occupies in a plane.
A rectangle's sides determine its area. In essence, the length and breadth of the rectangle multiplied together gives the area of the rectangle.
Let the length of the rectangle be (3x + 2) units and width of the rectangle be (4x + 10)units.
Area of rectangle = length × breadth
= (3x +2) × (4x +10)
simplifying the above equation, we get
= (3x) × (4x +10) + 2(4x +10)
= 12x² + 30x +8x +20
12x² + 38x + 20 = 0
simplifying the above equation, we get
By using quadratic equation, then
\($x_{1,2}=\frac{-38 \pm \sqrt{38^2-4 \cdot 12 \cdot 20}}{2 \cdot 12}$$\)
simplifying the above equation, we get
\($$\begin{gathered}x_{1,2}=\frac{-38 \pm 22}{2 \cdot 12}\end{gathered}$$\)
Separate the solutions, we get
\($$\begin{aligned}& x_1=\frac{-38+22}{2 \cdot 12}, x_2=\frac{-38-22}{2 \cdot 12} \\& x=\frac{-38+22}{2 \cdot 12}:-\frac{2}{3} \\& x=\frac{-38-22}{2 \cdot 12}:-\frac{5}{2}\end{aligned}$$\)
The solutions to the quadratic equation are:
\($x=-\frac{2}{3}, x=-\frac{5}{2}$$\)
The complete question is:
Find the area of rectangle with length (3x+2) units and width (4x+10)units.
To learn more about area refer to:
https://brainly.com/question/2607596
#SPJ1
how many sticky notes can hold a 205 pound man 20 holds a 165 pound man
Answers
Answer:
UH WHAT???!
Step-by-step explanation:
Someone please answer it’s 50 points!!
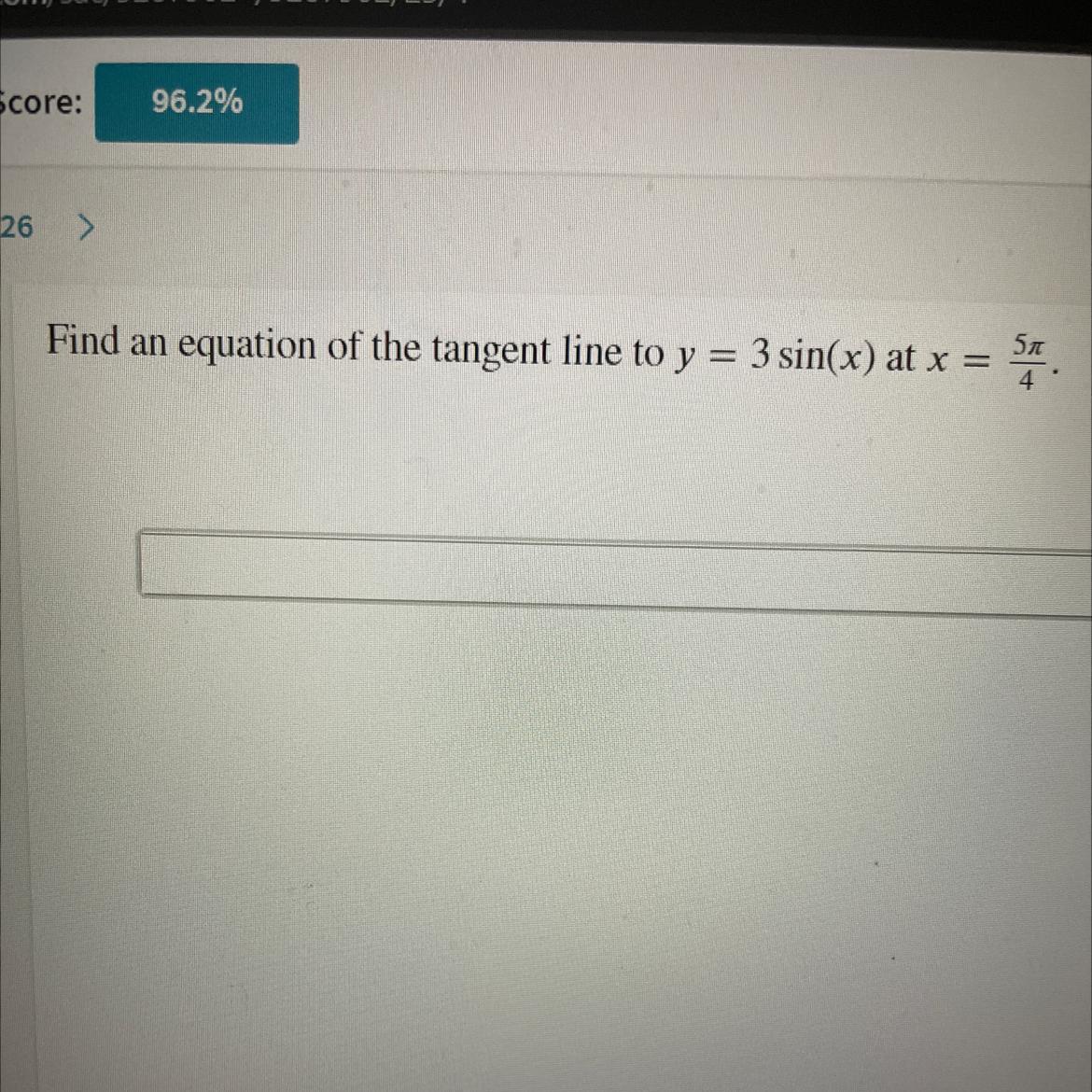
Answers
Hello!
Let's consider what the question asks for:
==> equation of tangent line to y = 3sin(x)
--> at: x = 5π/4
To find the slope of the line at a specific point on the function
--> MUST find the derivative of equation
\(\frac{d}{dx} 3sin(x)=3cos(x)\)
Derivative is function to find slope of function at every specific point
--> let's find the slope at x = 5π/4
\(3cos(x)=3*cos(\dfrac{5\pi }{4} )=3*(-\dfrac{\sqrt{2} }{2} )=-\dfrac{3\sqrt{2} }{2}\)
Now that we found the slope, we must also find the point at which the tangent line touches the function
--> simply plug x = 5π/4' to find y
\(y=3sin(\dfrac{5\pi }{4} )=-\dfrac{3\sqrt{2} }{2}\)
--> thus our point which the tangent line and function touch is
\((\dfrac{5\pi }{4},-\dfrac{3\sqrt{2} }{2} )\)
Now let's write our tangent line's equation in point-slope form:
\(y+\dfrac{3\sqrt{2} }{2} =-\dfrac{3\sqrt{2} }{2} (x-\dfrac{5\pi }{4})\) <== Answer
find the length of arc CDB. Round your answer to the nearest whole number. Leave your answer in terms of pi
Lenth of CDB=
Answers
Answer:
1
Step-by-step explanation:
1
PLease help, this is due tomorrow by 1 pm.

Answers
Note that the parameters of the graph a and graph b are given below.
Graph A - y=2(x-1)²
See graph attached.
Graph B - y = 1/2x² + 3
Vertex: The vertex of the function is (0, 3).
Axis of symmetry: The axis of symmetry is the vertical line passing through the vertex, which is x = 0.
Y-intercept: The y-intercept is the point where the graph intersects the y-axis. It is (0, 3).
Minimum or maximum: The coefficient of x² is positive, which means the parabola opens upwards, and therefore the function has a minimum value. The minimum value is 3.
Solutions: To find the solutions or roots of the quadratic equation, we need to set y or f(x) equal to zero and solve for x.
0 = 1/2 x² + 3
Subtracting 3 from both sides, we get:
-3 = 1/2 x²
Multiplying both sides by -2, we get:
6 = -x²
Taking the square root of both sides, we get:
x = ±√(-6)
Since the square root of a negative number is not a real number, the function has no real roots.
Minimum or maximum value: The minimum value of the function is 3.
Range: The range of the function is y ≥ 3, because the function has a minimum value of 3.
Domain: The domain of the function is all real numbers, because there are no restrictions on the values of x for which the function is defined.
Stretch/Shrink/Standard: The coefficient of x^2 is positive and less than 1, which means that the graph of the function is narrower than the graph of y = x². This is an example of a standard quadratic function that has been vertically compressed by a factor of 1/2.
See graph attached.
Learn more about graphs at:
https://brainly.com/question/17267403
#SPJ1


Suppose that the relation H is defined as follows. H = {(9, 3), (8, p), (3, q), (8, 0)) Give the domain and range of H. Write your answers using set notation.
Answers
Answer:
See below
Step-by-step explanation:
Domain would be all the x-values, so this is {3, 8, 8, 9}
Range would be all the y-values, so this is {0, 3, p, q}
I really need help!
What are the missing reasons in the proof?

Answers
Answer:
Step-by-step explanation:

Determine if the sequence is arithmetic. If it is, find the common difference, the 52nd term, the
explicit formula, and the recursive formula.

Answers
Hence Sequences 4, 16, 36, 64,.. are not arithmetic, however 40, 30, 20, 10,... are, with a common difference of -10 and the 52nd term being -490.
what is arithmetic progression ?An arithmetic progression is defined as a constant discrepancy between terms that follow one another through a series. For instance, the number sequence 5, 7, 9, 11, 13, and 15 is an example of either an exponential manner with a limitation of two. A progression with a set tolerance between any consecutive numbers is referred to as a "arithmetic progression" (A.P.). Two types of mathematical progression are possible: series in mathematics with a finite length A finite geographic progression is a serie with a finite number of terms. The early, delayed, tolerance, and frequency of terms may all be calculated using the terms in the series.
given
First succession
4, 16, 36, 64,
The common difference must be the same for it to be considered AP.
It is not AP since 16 - 4 ≠ 36 - 16.
Second succession;
40, 30, 20, 10, ...
common distinction =30 - 40 = 20 - 30 = 10 - 20 = -10
As a result, it will be an AP because the common difference is -10 and the same.
Now, The nth phrase of AP equals a plus (n - 1) d, where d is a typical difference and an is the initial term.
So, 52nd term = 40 + (52 - 1) (-10), which is -490.
Hence Sequences 4, 16, 36, 64,.. are not arithmetic, however 40, 30, 20, 10,... are, with a common difference of -10 and the 52nd term being -490.
To know more about arithmetic progression visit:
https://brainly.com/question/16947807
#SPJ1
What is the z score in the following data set, for the value of x = 14? Consider this data set to represent the entire population. Round to two decimal places, if necessary. 6, 12, 9, 8, 15, 5, 7, 10, 11, 13
Answers
The z score in the data set, for the value of x = 14 is 0.79
How to calculate the z-score of the data set?The data set is given as
6, 12, 9, 8, 15, 5, 7, 10, 11, 13
Start by calculating the mean of the data set using
Mean = Sum/Count
So, we have
Mean = (6 + 12 + 9 + 8 + 15 + 5 + 7 + 10 + 11 + 13)/10
Evaluate
Mean = 9.60
Using a statistical calculator, we have
SD = 3.04
The z-score is then calculated as
z = (x - Mean)/SD
So, we have
z = (12 - 9.60)/3.04
Evaluate
z = 0.79
Hence, the z score in the data set, for the value of x = 14 is 0.79
Read more about z score at
https://brainly.com/question/5512053
#SPJ1
i need help i dont get it comment if you need anything

Answers
Answer:
what is question 10?
Step-by-step explanation:
I need to find the answer in factored form and restrictions on the variable

Answers
Answer:
Option A
\(\begin{gathered} \frac{-2x(2x^{}+15)}{(x^{}-5)(x^{}-3)(x+3)} \\ x\neq-3,3,5 \end{gathered}\)Explanation:
Given the expression:
\(\frac{3x}{x^2-2x-15}-\frac{7x}{x^2-8x+15}\)First, factorize each quadratic expression.
\(\begin{gathered} =\frac{3x}{x^2-5x+3x-15}-\frac{7x}{x^2-3x-5x+15} \\ =\frac{3x}{x(x^{}-5)+3(x-5)}-\frac{7x}{x(x^{}-3)-5(x-3)} \\ =\frac{3x}{(x^{}-5)(x+3)}-\frac{7x}{(x^{}-3)(x-5)} \end{gathered}\)Next, find the lowest common multiple of the denominators:
\(=\frac{3x(x-3)-7x(x+3)}{(x^{}-5)(x^{}-3)(x+3)}\)Open the bracket in the numerator and simplify:
\(\begin{gathered} =\frac{3x^2-9x-7x^2-21x}{(x^{}-5)(x^{}-3)(x+3)} \\ =\frac{3x^2-7x^2-9x-21x}{(x^{}-5)(x^{}-3)(x+3)} \\ =\frac{-4x^2-30x}{(x^{}-5)(x^{}-3)(x+3)} \\ =\frac{-2x(2x^{}+15)}{(x^{}-5)(x^{}-3)(x+3)} \end{gathered}\)The restrictions on the variable are:
\(x\ne-3,x\ne3,x\ne5,\)
Find the x- and y-intercepts of the graph of x - y = 37. State each answer as an
integer or an improper fraction in simplest form.
Answers
The solution is, the x-intercept is (19,0) and the y-intercept is (0,-19).
What are y-intercept & x-intercepts of quadratic function?The y-intercept of the function is where the graph crosses y-axis.
The x-intercept is where the graph crosses the x-axis.
here, we have,
Given:
The equation of the graph is, x - y = 37.
The objective is to find the x-intercept and y-intercept of the graph.
Explanation:
At x-intercept the value of y will be zero.
In the given equation, at y = 0,
so, x - 0 = 37
or, x = 37
Thus, the coordinate is (37,0).
Similarly, at y-intercept the value of x will be zero.
In the given equation, at x = 0,
0-y = 37
or, y = -37
Thus, the coordinate is (0,-37).
Hence, the x-intercept is (19,0) and the y-intercept is (0,-19).
To learn more on y-intercept & x-intercepts of quadratic function click:
brainly.com/question/28822774
#SPJ9
Please find the volume of the figure

Answers
The volume of the pyramid is 576 cubic inches.
To find the volume of a square base pyramid, you can use the formula:
Volume = (1/3) x base area x height
In this case, the side of the square base is given as 12 inches, and the height is given as 12.5 inches.
First, calculate the base area of the pyramid:
Base area = side²
= 12²
= 144 square inches
Now, substitute the values into the volume formula:
Volume = (1/3) x 144 x 12.5
Volume = 576 cubic inches
Therefore, the volume of the pyramid is 576 cubic inches.
Learn more about Volume here:
https://brainly.com/question/13338592
#SPJ1
find the greatest common factor of 9n^4 and 4y^3
Answers
Answer:
1
Explanation:
The expressions 9n⁴and 4y³ have no term in common.
Therefore, the greatest common factor = 1
A manager at a local manufacturing company has been monitoring the output of one of the machines used to manufacture chromium shells. Past data indicate that if the machine is functioning properly, the length of the shells produced by this machine can be modeled as being normally distributed with a mean of 118 centimeters and a standard deviation of 8 centimeters. Suppose 16 shells produced by this machine are randomly selected. What is the probability that the average length of these 16 shells will be between 116 and 120 centimeters when the machine is operating "properly?" Please type your answer in 3 decimal places.
Answers
Answer:
0.682 = 68.2% probability that the average length of these 16 shells will be between 116 and 120 centimeters when the machine is operating "properly".
Step-by-step explanation:
To solve this question, we need to understand the normal probability distribution and the central limit theorem.
Normal Probability Distribution:
Problems of normal distributions can be solved using the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the z-score of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.
Central Limit Theorem
The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean \(\mu\) and standard deviation \(\sigma\), the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean \(\mu\) and standard deviation \(s = \frac{\sigma}{\sqrt{n}}\).
For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.
Normally distributed with a mean of 118 centimeters and a standard deviation of 8 centimeters.
This means that \(\mu = 118, \sigma = 8\)
Sample of 16 shells
This means that \(n = 16, s = \frac{8}{\sqrt{16}} = 2\)
What is the probability that the average length of these 16 shells will be between 116 and 120 centimeters when the machine is operating "properly?"
This is the pvalue of Z when X = 120 subtracted by the pvalue of Z when X = 116.
X = 120
\(Z = \frac{X - \mu}{\sigma}\)
By the Central Limit Theorem
\(Z = \frac{X - \mu}{s}\)
\(Z = \frac{120 - 118}{2}\)
\(Z = 1\)
\(Z = 1\) has a pvalue of 0.841
X = 116
\(Z = \frac{X - \mu}{s}\)
\(Z = \frac{116 - 118}{2}\)
\(Z = -1\)
\(Z = -1\) has a pvalue of 0.159
0.841 - 0.159 = 0.682
0.682 = 68.2% probability that the average length of these 16 shells will be between 116 and 120 centimeters when the machine is operating "properly".
Shaun White, the Flying Tomato, is rolling down a 30° ramp on his skateboard (because he's not just a snowboarding gold medalist, the bro can skate too). The total mass of Shaun and his skateboard is 75 kg. The rolling friction between the skateboard wheels and the concrete is 9N acting backward against the skateboard. The drag force due to air resistance is 11 N acting backwards against Shaun. What is Shaun's acceleration? 30° 4.64 m/s2 down the slope
Previous question
Answers
If the drag force due to air resistance is 11 N acting backwards against Shaun. Shaun's acceleration is 4.64 m/s^2 down the slope.
To find Shaun's acceleration, we need to calculate the net force acting on him and his skateboard. The net force is the vector sum of all the forces acting on the object. We can use Newton's second law of motion, which states that the net force acting on an object is equal to the product of its mass and its acceleration:
Net force = mass × acceleration
Let's break down the forces acting on Shaun and his skateboard:
The force of gravity, which acts vertically downwards with a magnitude of mg, where m is the total mass of Shaun and his skateboard and g is the acceleration due to gravity (9.8 m/s^2).
F₁ = m * g * sin(30°) = 75 kg * 9.8 m/s^2 * sin(30°) = 367.5 N
The force due to rolling friction between the skateboard wheels and the concrete, which acts backward against the skateboard.
F₂ = 9 N (given)
The drag force due to air resistance, which acts backward against Shaun.
F₃ = 11 N (given)
Now, let's add up the forces to get the net force:
Net force = F₁ - F₂ - F₃
= 367.5 N - 9 N - 11 N
= 347.5 N
Using Newton's second law of motion, we can now calculate Shaun's acceleration:
acceleration = Net force / mass
= 347.5 N / 75 kg
= 4.64 m/s^2 (down the slope)
To learn more about acceleration click on,
https://brainly.com/question/30647463
#SPJ4
Solve for the value of n.
(9n)
(8n+8)
Answers
Step by step explanation: no = so it’s no doable
This question is based on the given solving an equation. Therefore, the value of n for (9n) (8n+8) is 0 and -1.
Given:
(9n) (8n+8)
We need to determined the value of n.
According to the question,
It is given that, expression (9n) (8n+8).
For finding the value of n, we would be equate the given expression is equal to zero.
⇒ (9n) (8n+8) = 0
Now, calculating the value of n. We get,
⇒ (9n) (8n)+(9n) (8)
Then, solving above expression further. We get,
⇒ \(\bold{72 n^2+ 72n = 0}\)
Now, taking common 72 n. We get,
⇒ 72n (n + 1) = 0
⇒ 72 n = 0 and (n+1) = 0
We get,
n = 0 , -1
Therefore, the value of n for (9n) (8n+8) is 0 and -1.
For more details, prefer this link:
https://brainly.com/question/8743486
A city is approximately circular with a radius of 10.6 miles. Approximately 90,000 people live there. What is the population density of this city?
Answers
Answer:
513 people per square mile
Step-by-step explanation:
because
What is the 20th term of the sequence that begins -4,8,-16,32,...?
A. 1,048,576
B. 2,097,152
C. 524,288
D. -524,288
Answers
Answer:
B
Step-by-step explanation:
The 20th term of the sequence that begins as -4,8,-16,32,...is 2097152.
What is a geometric progression?
It is a type of sequence in which all the elements have common ratio. To calculate the common ratio we apply the following formula:
Ratio=a n/ a n-1
How to solve a geometric progression?
If we carefully watch our sequence we will be able to find that it is a geometric progression because all the terms have common ratio of -2.
To calculate the 20th term we will apply the formula:
20th term =\(ar^{20-1}\)
=-4* \((-2)^{19}\)
=-4*-524288
=2097152
Hence the 20 th term is 2097152.
Learn more about geometric progression at https://brainly.com/question/12006112
#SPJ2
what is 2-35 i rlly ned to know plz im 7 years olld
Answers
Answer:
-33
Step-by-step explanation:
Subtract 35-2 and you get 33. Now put a negative and it's -33! Super easy way to subtract them.
Answer:
33
Step-by-step explanation:
35 goses 34 the 33
find the sum of all the integers from 1 to 1000
Answers
Answer:
500500
Step-by-step explanation:
intergers are whole numbers which are not fractions
What percent of the front page is taken up by the
prom story, including the prom photograph?
A. 20%
B. 22%
C. 25%
D. 45%
E. 60%

Answers
The percent of the front page taken up by the prom story is 20%
Calculating the percent of the front page taken up by the prom storyFrom the question, we have the following parameters that can be used in our computation:
The front page
From the front page, we have
Area front page = 5 * 4
Area front page = 20
Also, we have
Prom = 2 * 2
Prom = 4
So, we have
Percentage = 4/20 * 100%
Evaluate
Percentage = 20%
Hence, the percent of the front page taken up by the prom story is 20%
Read more about percentage at
https://brainly.com/question/843074
#SPJ1
What does the transformation f(x)↦f(x)–8 do to the graph of f(x)
Answers
The transformation f(x) ↦ f(x) - 8 shifts the graph of f(x) downward by 8 units.
More specifically, for any value of x, the output of the function f(x) is subtracted by 8. This means that the y-coordinate of each point on the graph of f(x) is decreased by 8 units.
For example, suppose that point (a, b) lies on the graph of f(x). After applying the transformation f(x) ↦ f(x) - 8, the point (a, b - 8) lies on the transformed graph.
So, if the original graph of f(x) was above the x-axis, the transformed graph will be shifted downward and intersect the x-axis 8 units below where the original graph intersected it. If the original graph of f(x) was below the x-axis, the transformed graph will be shifted downward and move further away from the x-axis.
Learn more about transformation here:
https://brainly.com/question/13801312
#SPJ1
What's the solution to the following linear system?
y = 4x + 1
y = 4x
Question 4 options:
(−2, 3)
(4, 0)
Infinitely many solutions
No solution
Answers
Answer:
No solution
Step-by-step explanation:
4x = 4x + 1
0 unequal to 1
Answer: D. No solution
please mark Brainliest :)