Mattie is making a collar for her dog. She needs to buy some chain, clasp, and a name tag. She wants the chain to be 40 cm long. On meter of chain costs $9.75. The clasp is $1.29 and the name tag is $3.43. How much will it cost to make the collar? Estimate to check if your answer is reasonable.

Answer:

D)

Step-by-step explanation:

Answer:

-3x + 5y + 2.

Step-by-step explanation:

Answer:

25000

Step-by-step explanation:

it's independent because it's not related with her total sales s

Answer is:

A. Yes …..

===========================================================

Work Shown:

w = width

12+w = length, because it's 12 ft longer compared to the width.

P = perimeter of rectangle

P = 2*(length + width)

P = 2*(12+w + w)

P = 2(2w+12)

P = 4w+24

The perimeter 4w+24 must be 128 or larger

\(P \ge 128\\\\4w+24 \ge 128\\\\4w \ge 104\\\\w \ge 104/4\\\\w \ge 26\\\\\)

Therefore, the width must be 26 feet or longer.

The smallest value you can use is w = 26

If w = 26 is the width, then 12+w = 12+26 = 38 is the length

P = 2*(L+W) = 2*(38+26) = 2*(64) = 128 is the perimeter

This helps confirm the answer.

If triangle has a perimeter of 8x + 7. the first side of the triangle has a length of 4x, and the second side has a length of 2x − 3, the length of the third side of the triangle is 2x + 10.

To find the length of the third side of the triangle, we need to use the fact that the perimeter of a triangle is the sum of its three sides.

We are given that the perimeter of the triangle is 8x + 7, and we know the lengths of two sides: the first side has a length of 4x, and the second side has a length of 2x - 3. Let's use x as a common factor to simplify the expression for the perimeter:

Perimeter = 4x + (2x - 3) + (length of third side)

Perimeter = 6x - 3 + (length of third side)

8x + 7 = 6x - 3 + (length of third side)

Now we can solve for the length of the third side:

length of third side = 8x + 7 - 6x + 3

length of third side = 2x + 10

In general, when solving problems like this, it's important to remember that the perimeter of a triangle is the sum of its three sides, and to use algebraic equations to solve for unknown variables.

To learn more about triangle click on,

https://brainly.com/question/30293328

#SPJ4

Answer:

1.7 or square root of 2.9

Step-by-step explanation:

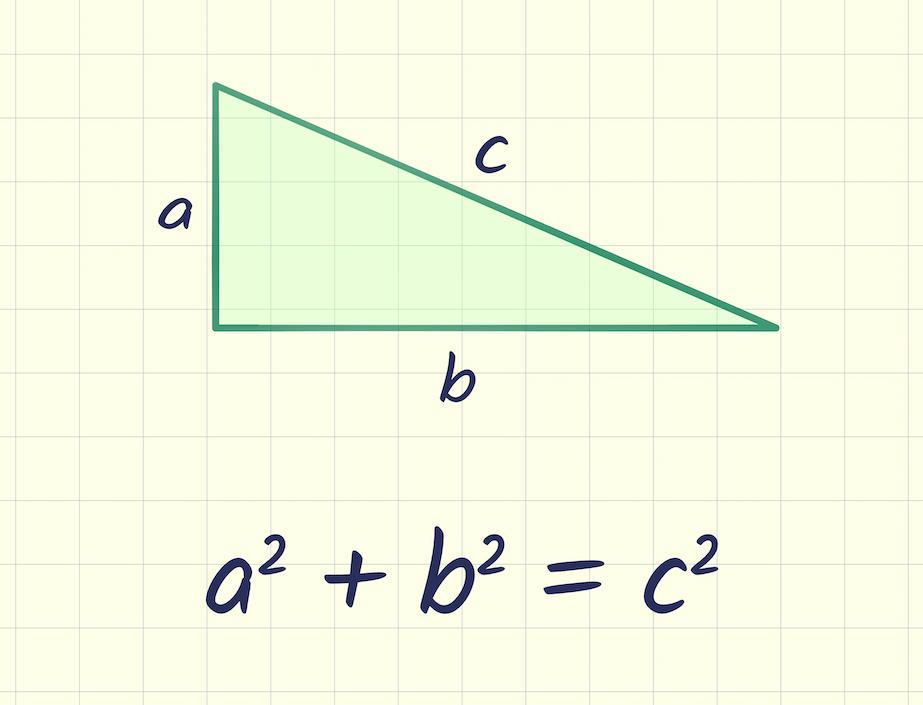
i remember how to do this its kind of simple really you just use the pythagorean theorem

The equation of the line that is perpendicular to y = -8x + 2 and contains the point (-4, 1) is y = (1/8)x + (3/2).

To find the equation of the line that is perpendicular to y = -8x + 2 and contains the point (-4, 1), first, determine the slope of the given line. The slope is -8. Perpendicular lines have slopes that are negative reciprocals of each other, so the slope of the new line will be 1/8.

Now, use the point-slope form of a linear equation, y - y1 = m(x - x1), where m is the slope and (x1, y1) is the given point (-4, 1). Plug in the values: y - 1 = (1/8)(x - (-4)).

Simplify the equation: y - 1 = (1/8)(x + 4). Distribute the 1/8: y - 1 = (1/8)x + (1/2). Finally, add 1 to both sides: y = (1/8)x + (1/2) + 1.

So, the equation of the line that is perpendicular to y = -8x + 2 and contains the point (-4, 1) is y = (1/8)x + (3/2).

To know more about perpendicular, refer here:

https://brainly.com/question/18271653#

#SPJ11

The property that justifies the statement "OP = RS, RS = OP" with "Sym" is symmetry. Symmetry refers to the property of an object or equation where it remains unchanged under certain transformations or operations.

In this case, if we reflect the circuit across the line of symmetry, the circuit will be exactly the same as the original circuit, except that the voltage source will be flipped over.

Therefore, if we take the voltage across the resistor (RS) and multiply it by the resistance of the voltage source (R), we will get the same result as if we take the voltage across the resistor (OP) and multiply it by the resistance of the resistor (R). This property is symmetric, and thus the statement "OP = RS, RS = OP" is true

Learn more about an object or equation

https://brainly.com/question/8751749

#SPJ4

Answer:

Sym. Prop. of ≅ is the correct answer

Hicksian demand functions are:x1** = 2P₁x₂ ; x₂** = P₂²

Utility function: u(x1+x2) = .5ln(x1) + .25ln(x₂) .The Marshallian demand functions are: x1* = - and x₂* = P₂.

The indirect utility function is found by substituting Marshallian demand functions into the utility function and solving for v(P₁, P₂, Y).u(x1*,x2*) = v(P₁,P₂,Y) ⇒ u(-, P₂) = v(P₁,P₂,Y) ⇒ .5ln(-) + .25ln(P₂) = v(P₁,P₂,Y) ⇒ v(P₁,P₂,Y) = - ∞ (as ln(-) is not defined)

Thus the indirect utility function is undefined.

Minimum expenditure function can be derived from the Marshallian demand function and prices of goods:

Exp = P₁x1* + P₂x2* = P₁(-) + P₂P₂ = -P₁ + P₂²

Minimum expenditure function is thus:

Exp = P₁(-) + P₂²

Hicksian demand functions can be derived from the utility function and prices of goods:

H1(x1, P1, P2, U) = x1*H2(x2, P1, P2, U) = x2*

Hicksian demand functions are:

x1** = 2P₁x₂

x₂** = P₂²

If there are no restrictions on the amount of money the consumer can spend, the Hicksian demand functions for x1 and x2 coincide with Marshallian demand functions.

Learn more about utility function at:

https://brainly.com/question/32708195

#SPJ11

A researcher conducted a study to investigate if a specific diet can help reduce blood pressure in people with high blood pressure. Participants were randomly assigned to a treatment group (following the diet) or a control group (not following the diet).

The mean blood pressure was calculated for both groups, and a 95% confidence interval for the difference in the means between the treatment and control groups was determined.

The interpretation of this 95% confidence interval is that, in 95 out of 100 similar experiments, the true difference in mean blood pressure between the treatment and control groups would fall within the calculated range. If the confidence interval does not include zero, it suggests that there is a significant difference between the treatment and control groups, meaning the diet may have a positive effect on reducing blood pressure. If the confidence interval includes zero, it indicates that the difference may not be statistically significant, and further research may be needed.

Know more about 95% confidence interval here:

https://brainly.com/question/15683202

#SPJ11

Answer:

9

Step-by-step explanation:

48 / 4 = 12

12 - 3 = 9

Check Work

9 + 3 = 12

12 * 4 = 48

Answer:

The formula for the volume of a cylinder is given by:

Volume = π * radius^2 * height

Given that the height of the cylinder is 10 centimeters and the radius is 19 centimeters, we can substitute these values into the formula and use the approximation of π as 3.14:

Volume = 3.14 * (19^2) * 10

Calculating the square of the radius:

Volume = 3.14 * 361 * 10

Multiplying the values:

Volume = 11354 * 10

Volume = 113540 cubic centimeters (rounded to the nearest hundredth)

So, the volume of the cylinder is approximately 113540 cubic centimeters.

The volume of a cylinder is calculated using the formula:

Volume = πr²h

where, π = 3.14

radius = 19 cm

Height = 10 cm

Volume = πr²h

= 3.14 × 19² × 10

= 3.14 × 361 × 10

= 11335.40 cm³

Given dimensions of rectangular design:

Width = w1 = 5 in

Length = l1 = 8 in

As mentioned, Katie uses a copy machine to enlarge her rectangular design. Therefore,

new width = w2 = 10 in

new length = l2 = x in

Katie creates a large copy of the original design. Therefore, the ratio of length to width must remain the same (as the original design). So, we can write as:

Now, let's put all the values in the equation

or

x = 16

Therefore, the new length would be 16.

The value of x_bar that makes vectors u and v orthogonal is

x_bar =−1.4.

To determine the value of x_bar such that vectors u=(0,2.8,2) and v=(1,1,x) are orthogonal, we need to check if their dot product is zero.

The dot product of two vectors is calculated by multiplying corresponding components and summing them:

u⋅v=u1⋅v 1 +u 2 ⋅v 2+u 3⋅v 3

​

Substituting the given values: u⋅v=(0)(1)+(2.8)(1)+(2)(x)=2.8+2x

For the vectors to be orthogonal, their dot product must be zero. So we set u⋅v=0:

2.8+2x=0

Solving this equation for

2x=−2.8

x= −2.8\2

x=−1.4

Therefore, the value of x_bar that makes vectors u and v orthogonal is

x_bar =−1.4.

To learn more about vectors visit: brainly.com/question/29740341

#SPJ11

Answer:

-1

Step-by-step explanation:

Answer:

The line would be verticle or up and down, since the x coordinate is the same it would be up and down

funciton is y=2

4x-7 =5

4x=5+7

x= 12/4

x=3

Answer:

1.) Volume= Whereas the basic formula for the area of a rectangular shape is length × width, the basic formula for volume is  Length × Width × Height

2.) Terms in this set (4)

Measure 50 ml of water into a gradulated cylinder.

Place object in cylinder and measure the new volume.

Subtract the 50ml from the new volume.

The difference in the volume is the volume. of the object.

3.) Graduated cylinders

4.) Particles behave differently within each state of matter: solid, liquid, and gas. The particles give matter a property called mass. The mass of an object is related to the amount of material that makes up the object and how hard the object is to move. Simple experiments can show how gases have mass.

Explanation:

1.) Volume is the quantity of three-dimensional space enclosed by a closed surface, for example, the space that a substance (solid, liquid, gas, or plasma) or shape occupies or contains. Volume is often quantified numerically using the SI derived unit, the cubic metre.

SI unit: Cubic metre

In SI base units: 1 m3

2.) If the object has an irregular shape , the volume can be measured using a displacement can . The displacement can is filled with water above a narrow spout and allowed to drain until the water is level with the spout. As the irregular object is lowered into the displacement can, the water level rises.

3.) Today they will practice measuring different liquids. They will use a container called a graduated cylinder to measure liquids. Graduated cylinders have numbers on the side that help you determine the volume. Volume is measured in units called liters or fractions of liters called milliliters (ml).

4.) Mass is a measure of the amount of matter in an object. Mass is usually measured in grams (g) or kilograms (kg). ... An object's mass is constant in all circumstances; contrast this with its weight, a force that depends on gravity. Your mass on the earth and the moon are identical.

~-Long Story short, its 1 = Degree of Length

                                     1 = Degree of Width

                                     3 = Degree of Height       That's is all summed up!-~

                                     5 = Degree of Volume

                   Ⓗⓞⓟⓔ ⓣⓗⓘⓢ Ⓗⓔⓛⓟⓔⓓ❕  

                                                              ~

The degrees of the given dimensions are degree of length= 1 ,degree of width = 1 , degree of height= 3 , degree of volume = 5

To determine the degree of each dimension and the volume for Box 2, let's consider the expressions:

Length = (4x - 1)

Width = x

Height = x³

Volume = Length × Width × Height

Volume = (4x - 1) × x × x³

Now, let's simplify the volume expression:

Volume = (4x² - x) × x³

Volume = 4x⁵ - x⁴

Now, let's find the degrees of each dimension and the volume:

Degree of length:

The degree of the length dimension is the highest power of x in the expression (4x - 1). The highest power of x in this expression is 1.

Degree of width:

The degree of the width dimension is the highest power of x in the expression x. The highest power of x in this expression is 1.

Degree of height:

The degree of the height dimension is the highest power of x in the expression x³. The highest power of x in this expression is 3.

Degree of volume: The degree of the volume is the highest power of x in the expression 4x⁵ - x⁴. The highest power of x in this expression is 5.

Therefore, the degrees are as follow,

Degree of length: 1

Degree of width: 1

Degree of height: 3

Degree of volume: 5

learn more about degrees here

brainly.com/question/30217674

#SPJ2

x intercept The x intercept is the point where the line crosses the x axis. At this point y = 0.

Answer:

I believe the answer is C. Please let me know if I am wrong

Step-by-step explanation:

John's savings amount as a function of time is S(t) = $24,000 / 25. Initially, he needs to save $24,000 for a new car. After the first month, he has saved $1,000. The savings amount is directly proportional to the time elapsed. The constant of proportionality is 1/24. Thus, John's savings amount can be determined based on the remaining amount he needs to save.

John's savings amount can be represented as a function of time and is proportional to the amount he still needs to save. Let's denote the amount John needs to save as N(t) at time t, and his savings amount as S(t) at time t. Initially, John needs to save $24,000, so we have N(0) = $24,000.

We know that John has saved $1,000 after the first month, which means S(1) = $1,000. Since his savings amount is proportional to the amount he still needs to save, we can write the proportionality as:

S(t) = k * N(t)

where k is a constant of proportionality.

We need to find the value of k to determine John's savings amount at any given time.

Using the initial values, we can substitute t = 0 and t = 1 into the equation above:

S(0) = k * N(0)  =>  $1,000 = k * $24,000  =>  k = 1/24

Now we have the value of k, and we can write John's savings amount as a function of time:

S(t) = (1/24) * N(t)

Since John's savings amount is proportional to the amount he still needs to save, we can express the amount he still needs to save at time t as:

N(t) = $24,000 - S(t)

Substituting the expression for N(t) into the equation for S(t), we get:

S(t) = (1/24) * ($24,000 - S(t))

Simplifying the equation, we have:

24S(t) = $24,000 - S(t)

25S(t) = $24,000

S(t) = $24,000 / 25

Therefore, John's savings amount at any given time t is S(t) = $24,000 / 25.

To know more about proportional savings, refer here:

https://brainly.com/question/29251832#

#SPJ11

Answer:

The length is 15.71 feet.

Step-by-step explanation:

Therefore, After 20 minutes, there are approximately 11.9 kg (rounded to one decimal place) of salt in the tank.

To solve this problem, we need to consider the rate of change of the amount of salt in the tank over time.

(a) Let's denote the amount of salt in the tank after t minutes as y (in kg). We can set up a differential equation to represent the rate of change of salt:

dy/dt = (rate of salt in) - (rate of salt out)

The rate of salt in is given by the concentration of salt in the incoming water (0 kg/L) multiplied by the rate at which water enters the tank (90 L/min). Therefore, the rate of salt in is 0 kg/L * 90 L/min = 0 kg/min.

The rate of salt out is given by the concentration of salt in the tank (y kg/9000 L) multiplied by the rate at which water leaves the tank (90 L/min). Therefore, the rate of salt out is (y/9000) kg/min.

Setting up the differential equation:

dy/dt = 0 - (y/9000)

dy/dt + (1/9000)y = 0

This is a first-order linear homogeneous differential equation. We can solve it by separation of variables:

dy/y = -(1/9000)dt

Integrating both sides:

ln|y| = -(1/9000)t + C

Solving for y:

y = Ce^(-t/9000)

To find the particular solution, we need an initial condition. We know that at t = 0, y = 12 kg (the initial amount of salt in the tank). Substituting these values into the equation:

12 = Ce^(0/9000)

12 = Ce^0

12 = C

Therefore, the particular solution is:

y = 12e^(-t/9000)

(b) To find the amount of salt in the tank after 20 minutes, we substitute t = 20 into the particular solution:

y = 12e^(-20/9000)

y ≈ 11.8767 kg (rounded to one decimal place)

Learn more about equation here:

https://brainly.com/question/29538993

#SPJ11

Answer:

52,488

Step-by-step explanation:

First 2187 multiplied by $1 equals $2187

Second 2187 times 3 equals 6561

Third 6561 times 7 equals 52,488

To find the extremum of the function f(x,y) = 2x² + 2y² subject to the constraint 3x + y = 60, we can use the method of Lagrange multipliers. By setting up the Lagrange function F(x,y,λ) = 2x² + 2y² - λ(3x + y - 60) and calculating the partial derivatives Fx, Fy, and Fλ, we can find the critical points. From there, we can determine whether the extremum is a maximum or a minimum.

To find the extremum of f(x,y) subject to the constraint, we set up the Lagrange function F(x,y,λ) = 2x² + 2y² - λ(3x + y - 60), where λ is the Lagrange multiplier. Next, we calculate the partial derivatives Fx, Fy, and Fλ by differentiating F with respect to x, y, and λ, respectively.

By setting Fx = 0, Fy = 0, and the constraint equation 3x + y = 60, we can solve for the critical points (x, y). From there, we can determine whether each critical point corresponds to a maximum or a minimum by considering the second partial derivatives.

The extremum of the function will occur at the critical point that satisfies the constraint and corresponds to a minimum or a maximum based on the second partial derivatives. To determine the specific value of the extremum, we would substitute the coordinates of the critical point into the function f(x,y) = 2x² + 2y².

Learn more about  function here:

https://brainly.com/question/31062578

#SPJ11

The null hypothesis (H₀) is typically that the population mean is equal to a certain value. However, you haven't specified a null hypothesis in your question. Please provide the null hypothesis so that I can assist you further in determining the decision rule.

To determine the decision rule for rejecting the null hypothesis, we need to establish the critical value(s) or the rejection region based on the level of significance.

Given:

Sample size (n) = 18

Sample mean (x(bar)) = 5.6 pounds/square inch

Standard deviation (σ) = 0.8

Level of significance (α) = 0.01

Since the population distribution is assumed to be approximately normal, we can use the Z-test.

To know more about distribution visit:

brainly.com/question/33255942

#SPJ11

Answer:

y-intercept: (0, -0.7)

x-intercept: (-1.2, 0)

Step-by-step explanation:

In the given figure

∵ The line intersects the y-axis at the point (0, -0.7)

∴ The point of intersection between the line and the y-axis is (0, -0.7)

→ By using the 2nd note above

∴ The y-intercept is (0, -0.7)

∵ The line intersects the x-axis at the point (-1.2, 0)

∴ The point of intersection between the line and the x-axis is (-1.2, 0)

→ By using the 1st note above

∴ The x-intercept is (-1.2, 0)

Answer:

1 / 4

Step-by-step explanation:

Total number of marbles = 40 + 50 + 30 + 80 = 200

There are 50 green marbles,

So, 50 / 200 = 1 / 4

Answer:

The answer is B.

Step-by-step explanation:

When you reflect (2,5) over the x axis, you get (2,-5).