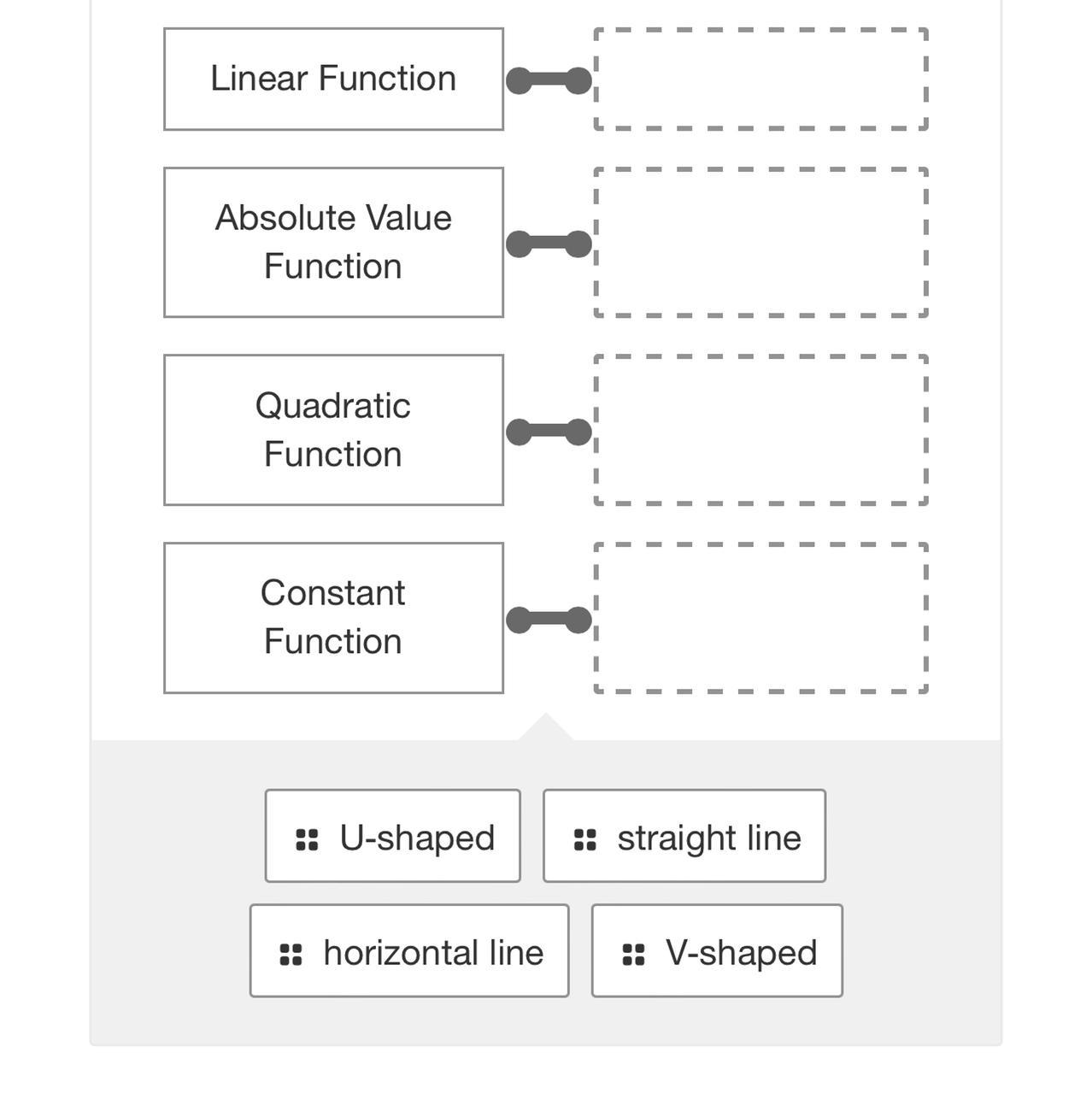
Match the title of the parent functions with thedescription of the graph of the function.
Answers
Answer:
Linear function: straight line
absolute value function: V-shaped
Quadratic function: U shaped
Constant function: horizontal line
Explanation:
A linear function is a straight line when represented on a graph.
A constant function has a slope of zero. Thus, when it is plotted on the graph, the line is horizontal.
When we plot a quadratic function on a graph, the result is a parabola. A parabola has a curved shape
When we plot an absolute value function on a graph, the result would be two straight lines forming a v shape.
Related Questions
will give brainliest

Answers
Explanation
If (a^2 + b^2) (x^2 +y^2) = (ax + by )^2 then which relation is true?
Answers
Answer:
Step-by-step explanation:
Hello,
Let's develop both expressions and try to re factorise.
\(\forall (a,b,x,y) \in \mathbb{R}^4 \\ \\ (a^2+b^2)(x^2+y^2)=(ax+by)^2\\ \\<=>(ax)^2+(ay)^2+(bx)^2+(by)^2=(ax)^2+(by)^2+2(ax)(by)\\ \\<=> (ay)^2+(bx)^2-2(ay)(bx)=0\\ \\<=> (ay-bx)^2=0\\ \\<=> ay-bx=0\\ \\<=> \boxed{\sf \bf ay=bx}\)
Thanks
Find the equation of a line which is perpendicular to y = 1/2x - 5 and goes throught the point (0, 0). Write your answer in the form y=mx+c.
Answers
Answer: y = -2x
Step-by-step explanation:
For a line to be perpendicular to another, it must have the opposite reciprocal slope. In this case, that means 1/2 becomes -2/1 or -2. For the line to pass through 0,0 the y intercept must be 0. Thus the line is y = -2x + 0, or y = -2x
Which mixed number is equivalent to
19/3
Answers
Answer:
6 1/3
Step-by-step explanation:
You just have to see how many times it goes into it
Write one quadratic equation that forms a graph through the points (-4,2) and (1,2) and has aminimum value at the vertex.
Answers
The general form of a quadratic formula is
\(f(x)=ax^2+bx+c\)where a,b and c are constants. Also, note that a is a constant that helps to determine the shape of the function. As we want that the vertex is a minimum, we are in the following situation
so, this adds the restriction that a>0.
Now, we are given the points (-4,2) and (1,2). We can replace this values in our function. Let us do that with (-4,2). So we get
\(a(-4)^2+b(\text{ -4)+c=2}=16a\text{ -4b+c}\)if we do that with the other point we get
\(a(1)+b(1)+c=2=a+b+c\)so if we make this two equations equal, we have
\(16a\text{ - 4b+c = a+b+c}\)so if we subtract c on both sides, we get
\(16a\text{ -4b=a+b}\)we can subtract a and b from both sides, so we get
\(16a\text{ -4b -a -b =15a -5 b=0}\)so if we divide both sides by 5 we get
\(3a\text{ - b=0}\)This means that we can give values to a and b freely. Recall that a must be positive. So let us choose a=1 and b=3. So our equation becomes
\(x^2+3x+c\)Now we need to give values for c. Note that if x = -4, we have that
\((-4)^2+3(\text{ -4)+c=16 -12 + c=2=4+c}\)so, we subtract c 4 from both sides and we get
\(c=2\text{ -4= -2}\)So our equation becomes
\(f(x)=x^2+3x\text{ - 2}\)Let us check that it passes through the other point. Note when x=1 we have
\(1^2+3\cdot1\text{ -2 = 1 +3 -2 = 4 -2 =2}\)so this equation fulfills the task

Please help me I need help with algebra 2

Answers
Answer:If (x + 1) is a factor of the polynomial p(x), then p(x) can be written as:
p(x) = (x + 1) q(x)
for some polynomial q(x). By substituting x = -1 into this expression, we can find the value of c:
p(-1) = (-1 + 1) q(-1) = 0 q(-1) = 0
So,
0 = 5(-1)^4 + 7(-1)^3 - 2(-1)^2 - 3(-1) + c
= -5 + 7 - 2 + 3 + c
= c = 3
So, the value of c that makes (x + 1) a factor of the polynomial p(x) = 5x^4 + 7x^3 - 2x^2 - 3x + c is c = 3.
what is the length of line ab?
Answers
Find a vector equation and parametric equations for the line through the point (1,0,6) and perpendicular to the plane x+3y+z=5.
Answers
The normal vector to the plane x + 3y + z = 5 is n = (1, 3, 1). The line we want is parallel to this normal vector.
Scale this normal vector by any real number t to get the equation of the line through the point (1, 3, 1) and the origin, then translate it by the vector (1, 0, 6) to get the equation of the line we want:
(1, 0, 6) + (1, 3, 1)t = (1 + t, 3t, 6 + t)
This is the vector equation; getting the parametric form is just a matter of delineating
x(t) = 1 + t
y(t) = 3t
z(t) = 6 + t
The vector equation for the line through the point (1,0,6) and perpendicular to the plane x+3y+z=5 is v =(1+t)i + (3t)j + (6+t)k
The parametric equations for the line through the point (1,0,6) and perpendicular to the plane x+3y+z=5
x(t) = 1+ty(t) = 3tz(t) = 6+tThe parametric equation of a line through the point A(x, y, z) perpendicular to the plane ax+by+cz= d is expressed generally as:
A + vt where:
A = (x, y, z)
v = (a, b, c) (normal vector)
This can then be expressed as:
s = A + vt
s = (x, y, z) + (a, b, c)t
Given the point
(x, y, z) = (1,0,6)
(a, b, c) = (1, 3, 1)
Substitute the given coordinate into the equation above:
s = (1,0,6) + (1, 3, 1)t
s = (1+t) + (0+3t) + (6+t)
The parametric equations from the equation above are:
x(t) = 1+t
y(t) = 3t
z(t) = 6+t
The vector equation will be expressed as v = xi + yj + zk
v =(1+t)i + (3t)j + (6+t)k
Learn more here: brainly.com/question/12850672
HELP!!!! It’s for homework. I will give brainly

Answers
Answer:
V = a^7b^3
Step-by-step explanation:
Volume = length × width × height
Vol =
a^2 × a^4b^2 × ab
This is all multiplication, so we can rearrange.
a^7b^3
This is a to the seventh power times b to the 3rd power.
Which statements are true about the graph of y s 3x + 1 and y 2 -x + 2? Check all that apply.
O The slope of one boundary line is 2.
O Both boundary lines are solid.
A solution to the system is (1, 3).
O Both inequalities are shaded below the boundary lines
O The boundary lines intersect.

Answers
===========================================================
Explanation:
Let's go through each of the answer choices to see which are true and which are false.
----------------
Choice A
The general slope intercept form is y = mx+b
m = slope and b = y intercept.
For y = 3x+1, the boundary line of the first inequality, the slope is 3.
For y = -x+2, the slope is -1.
None of the slopes are 2.
Choice A is false.
We'll use the concept of slope again in choice E.
----------------
Choice B
The "or equal to" part of the inequality sign is what directly determines the boundary line being solid. This is because we include points on the boundary.
Choice B is true.
----------------
Choice C
Plug x = 1 and y = 3 into the first inequality
\(y \le 3x+1\\\\3 \le 3(1)+1\\\\3 \le 3+1\\\\3 \le 4\\\\\)
The last inequality is true, so the first inequality is true when (x,y) = (1,3). This makes (1,3) a solution to \(y \le 3x+1\\\\\)
Repeat those steps for the other inequality given to us
\(y \ge -x+2\\\\3 \ge -1+2\\\\3 \ge 1\\\\\)
which is also true, so that makes (1,3) also a solution to \(y \ge -x+2\\\\\)
The point (1,3) is a solution to both inequalities at the same time, making it a solution to the system overall.
Choice C is true
----------------
Choice D
When y is fully isolated, the "less than" inequality indicates the shading is below the boundary. This is due to us considering points of y coordinates smaller than the boundary line. So we'll shade below the boundary for \(y \le 3x+1\\\\\)
We don't do the same for \(y \ge -x+2\\\\\). Instead, we'll shade above the solid boundary line.
Choice D is false.
----------------
Choice E
If two lines have equal slopes, but different y intercepts, then we have parallel lines. Parallel lines never intersect.
If on the other hand, the slopes are different values, then the two lines will intersect somewhere on the xy grid. There will only be exactly one point of intersection.
The given system has boundary lines of slopes 3 and -1, for the first and second inequality respectively. Refer back to choice A. These differing slopes tell us that the boundary lines intersect somewhere.
Choice E is true
Let's go through all the options one at a time and look for the correct ones
Option 1: The slope of one boundary line is 2
We have 2 equations of lines, where the coefficients of are 3 and -1 respectively
because the coefficient of x denotes the slope of a line, we know that the lines have the slope 3 and -1, not 2
Hence, this option is Incorrect
Option 2: Both boundary lines are solid
In order for the boundary lines to be solid, the inequality must have an 'equal to', like ≤ (less than or equal to) or ≥ (greater than or equal to)
we can see that that's the case in our case and hence, this option is Correct
Option 3: A solution to the system is (1, 3)
To confirm this, we'll plug these coordinates into the given inequalities and see if it stands correct
y ≤ 3x + 1
3 ≤ 3(1) + 1
3 ≤ 4 which is correct because 3 is less than 4
Second equation:
y ≥ 2 - x
3 ≥ 2 - 1
3 ≥ 1
Which is also true because 3 is greater than 1
Now, we can say that (1 , 3) is a solution to the system because it satisfies both the equations and is Correct
Option 4: Both inequalities are shaded below the boundary lines
For an inequality to be shaded below the boundary line, it must have the ≤ inequality (in case of solid line) and < inequality (in case of dotted line)
because the second inequality listed includes the ≥ inequality, which was not mentioned above, it won't be shaded below
another way to think about it is that any 'greater than' inequality will shade everything above the line and the 'lesser than' inequality will shade below the line
which means that this option is Incorrect
Option 5: The boundary lines intersect
In order for the boundary lines to intersect, they must have have different slopes.
as we mentioned in the explanation of the first option, that the slopes of the lines is 3 and -1, which are different slopes
Therefore, this option is Correct
If every 2 cm on a scale drawing is equal to 7 feet in real life, which lines on the drawing would be greater than 21 feet in real life? Select all that apply. A) 7 cm B) 5 cm C) 9 cm D) 12 cm
Answers
The correct answers are A) 7cm, C) 9cm and D) 12cm
Define the Conversion of units?The process of changing a given quantity that is expressed in one unit of measurement to another unit of measurement that is equivalent in value is referred to as conversion of units.
If every 2 cm on a scale drawing is equal to 7 feet in real life, then we can use proportions to find out which lines on the drawing would be greater than 21 feet in real life.
Let x be the length of a line on the scale drawing in centimeters. Then, we can set up the following proportion:
⇒ \(\frac{2cm}{7 feet} = \frac{x cm }{yfeet}\)
where y is the length of the line in real life. Solving for y, we get:
⇒ \(y = \frac{7 feet} {2cm} *x\)
⇒ \(y = 3.5 x feet\)
If we put x = 2cm (given) then, y = 7 feet
For y = 21 feet, the value of x = 6cm.
Therefore, any line on the scale drawing that is greater than 6cm in length corresponds to a length greater than 21 feet in real life.
So, the lines on the drawing that are greater than 21 feet in real life are:
A) 7cm, C) 9cm, D) 12cm
Therefore, the correct answers are A) 7cm, C) 9cm and D) 12cm
To know more about conversion, visit:
https://brainly.com/question/13016491
#SPJ1
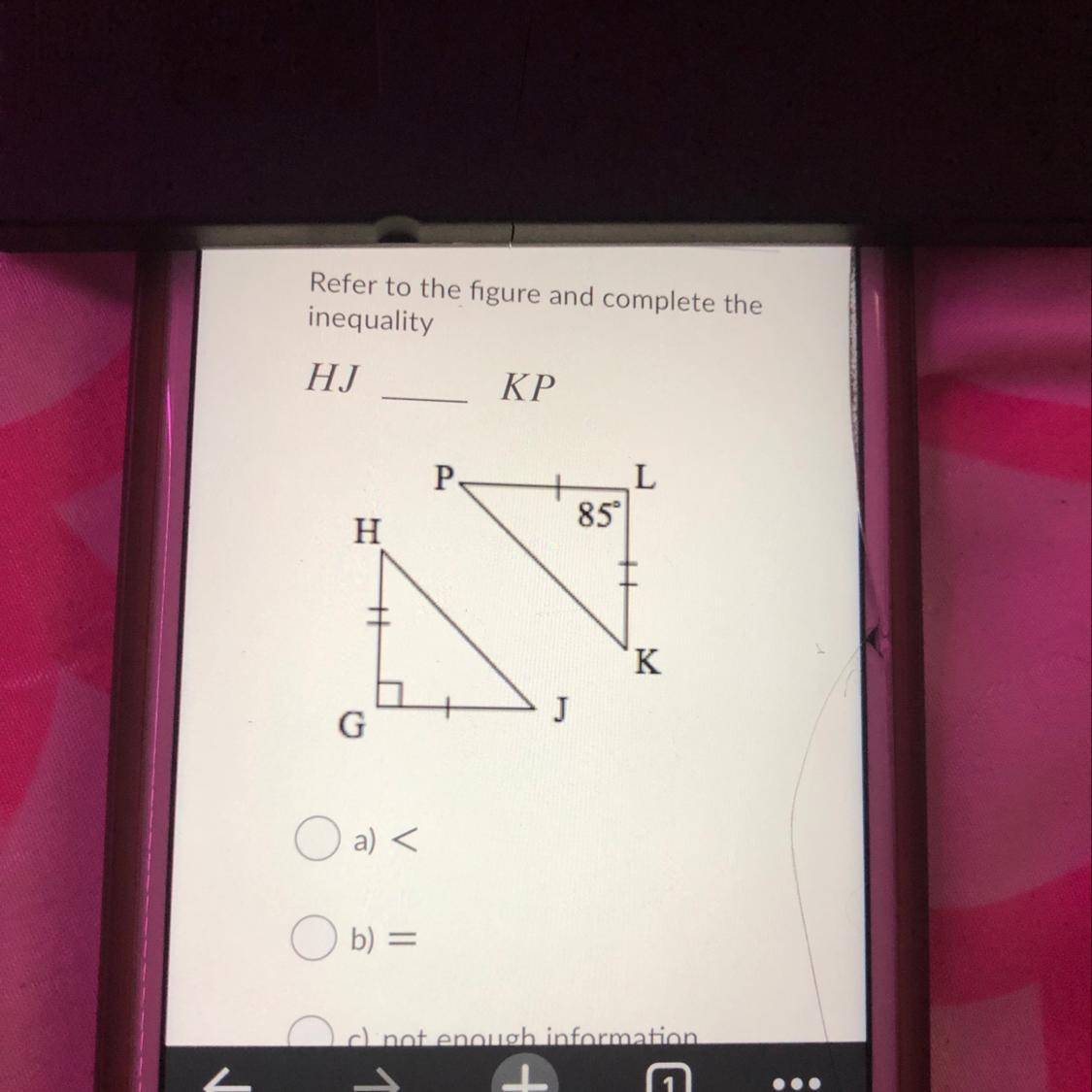
NEED GEOMETRY HELP ASAP
Answers
Answer:
HJ > KP
Step-by-step explanation:
Form the figure attached,
Two triangles PKL and JGH have been given with HG ≅ KL and PL ≅ GJ
m∠HGJ = 90°
m∠KLP = 85°
Since m∠HGJ > m∠PLK
Therefore, measure of opposite sides of these angles have the same relation.
HJ > KP
Estimate a 10% tip on a restaurant bill of $75.28.
Answers
8 dollars
Step-by-step explanation:
without rounding it is $7.52 but you would round that to 8
Multiply
-1 2/3 • ( -5 1/4 )

Answers
Answer:
Positive 8 3/4
Step-by-step explanation:
My way:
-1 2/3 times -5 1/4
- 1 2/3 simplifies to -5/3
-5 1/4 simplifies to -21/4
-5/3 times -21/4 is 35/4
Simplify that which is 8 3/4
(negative times negative = positive)
Find m∠2 if m∠4 = 130°.

Answers
m = 130 degrees
i need help please:)

Answers
Hshdhshsjdjshsuusudushwvagsgyswuuw
/\_/\
( ●.●)
\ /
<=={}=====>
meow meow hahaha
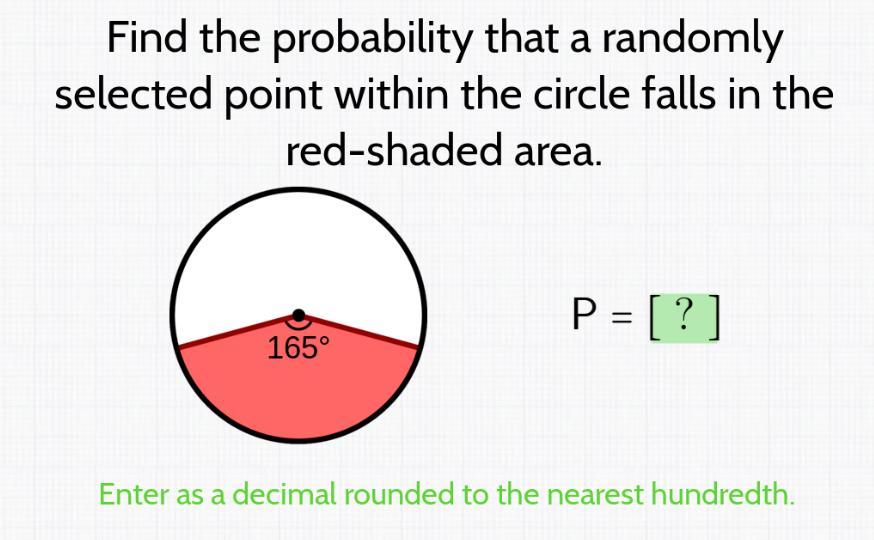
GIVING BRAINLIST PLEASE HELP!!!
Answers
The probability that a randomly selected point within the circle would fall in the red- shaded area is 45. 833 %
How to find the probability ?The arc that is covered by the red - shaded area in the circle has a degree measure of 165 degrees. This is out of the total circle angle measure of 360 degrees.
This therefore means that the probability that a randomly selected point within the circle would fall in the red- shaded area can be found to be :
= Angle measure of red - shaped area / Total area x 100 %
= 165 / 360 x 100 %
=0. 45833 x 100 %
= 45. 833 %
Find out more on probability at https://brainly.com/question/22690728
#SPJ1
Suppose a parabola has an axis of symmetry at x = -1, a maximum height of –1 and also passes through the point (0, –5). Write the equation of the parabola in vertex form.
Answers
The vertex form of the parabola is y + 1 = - 4 · (x + 1)².
How to determine the vertex form of the equation of a parabola
Graphically speaking, parabolae can be generated by quadratic equations, whose forms are described below: (Please notice that the parabola described by statement is parallel to y-axis since axis of symmetry is a vertical line)
Standard form
y = a · x² + b · x + c
Vertex form
y - k = C · (x - h)²
Where:
x - Independent variabley - Dependent variablea, b, c - Real coefficient(h, k) - Coordinates of the vertex.If we know that h = - 1, k = - 1 and (x, y) = (0, - 5), then the equation of the parabola in vertex form is:
C = (y - k) / (x - h)²
C = (- 5 + 1) / (0 + 1)²
C = - 4 / 1²
C = - 4
The equation of the parabola in vertex form is equal to y + 1 = - 4 · (x + 1)².
To learn more on quadratic equations: https://brainly.com/question/1863222
#SPJ1
Rewrite the following function in factored form. f(x)=x2+6x+8
Answers
Answer:
f(x) = (x+2)(x+4)
Step-by-step explanation:
4 + 2 = 6
4 * 2 = 8
f(x) = (x+2)(x+4)
Graph the circle (x-3)^2+(y-7)^2=4

Answers
x-3 and y-7 represents the shift in the centre of the circle in the respective axis. Therefore the centre is (3,7). r=2. d=4. So this circle’s centre is at (3,7) with radius 2.
Tania paid $9.80 for 2.8 pounds of cherries . What is the price per pound of cherries?
Answers
Answer:
The price for one pound of cherries is $3.5
Step-by-step explanation:
$9.8/2.8= $3.5 for one pound of cherries
xoxo, your highness...Answer:
$3.50
Step-by-step explanation:
Divide 9.80 by 2.8 and add a zero to get $3.50 per pound. Hope this helps.
The expression below represents the profit, in dollars, a movie theater makes when n customers attend a movie
3.5n-175 which of these is an equivalent expression that reveals the number of customers required for the movie theater to break even (have a profit of $0)?
A.3.5(n-175)
B.3.5(n-50)
C.-171.5n
D.175-3.5n
Answers
Answer:
a
Step-by-step explanation:
HELP, this is due in 20 minutes!!!!PLEASE
The diagram contains contradictory information. Explain the contradiction.
A. Since
When you solve for x, you get 0=180. This is equally not valid.
B. Since
When you solve for x, you get x=30.
This would make m
An angle cannot measure 0 degrees, because it would not exists.
C. Since
When you solve for x, you get 0=180.
This equality is not valid.
D. Since
When you solve for x, you get x = 30.
This would make m
An angle cannot measure 0 degrees.

Answers
solve: 2/x+3 - 1/x = -4/x^2+3x
You must show your work and enter your answer below.
Answers
The solution of the linear equation is determined as x = -4.
What is the solution of the linear equation?
The solution of the linear equation is calculated by applying the following method as follows;
The given linear equation;
2/x+3 - 1/x = -4/x² +3x
We can start by simplifying the equation and getting rid of the fractions.
Multiplying every term by x will help us achieve that:
2 + 3x - 1 = -4/x + 3x²
Simplifying further:
2 + 3x - 1 = (-4 + 3x²) / x
Combining like terms:
3x + 1 = (-4 + 3x²) / x
(x)(3x + 1) = -4 + 3x²
3x² + x = -4 + 3x²
We can subtract 3x² from both sides:
x = -4
Learn more about linear equations here: https://brainly.com/question/28732353
#SPJ1
4. For each babysitting job, Adam charges a fee for his bus fare plus an hourly rate. The graph shows how he calculates the cost of a babysitting job. Write a linear function in the form
y = mx + b to represent the situation.
Ay = 3x+2
B. y = 3x+1
C. y = 6x+2
D. y = -6× + 2
Answers
y = 6x + 2 is the function which Adam charges a rate of $6 per hour and an additional fee of $2 for the bus fare.
The linear function in the form y = mx + b represents the situation where y represents the cost of the babysitting job
x represents the number of hours, "m" represents the hourly rate, and "b" represents the additional fee (bus fare).
y = 3x + 2 represents an hourly rate of 3 and an additional fee of 2.
y = 3x + 1 represents an hourly rate of 3 and an additional fee of 1.
y = 6x + 2 represents an hourly rate of 6 and an additional fee of 2.
y = -6x + 2 represents a negative hourly rate of -6 and an additional fee of 2.
Hence, y = 6x + 2 is the which Adam charges a rate of $6 per hour and an additional fee of $2 for the bus fare.
To learn more on Equation:
https://brainly.com/question/10413253
#SPJ1
Height of redwood trees is normally distributed, with a mean of 360 feet, and a standard deviation of 10 feet. Using this information and a z-score table, find the percentile for a redwood tree that is 375 feet tall. a. 13thb. 95th c. 80thd. 93rd
Answers
The percentile for a redwood tree that is 375 feet tall would be 93rd percentile. This is because the z-score of 1.5 (375-360/10) corresponds to a percentile of 93.
Step 1: Find z-score
z-score = (375-360)/10 = 1.5
Step 2: Find percentile
Using a z-score table, the percentile corresponding to a z-score of 1.5 is 93.
Therefore, the percentile for a redwood tree that is 375 feet tall is 93rd percentile.
The percentile of a redwood tree that is 375 feet tall can be determined using a z-score table. The z-score of a data point is the difference between the data point and the mean, divided by the standard deviation. In this case, the z-score is (375-360)/10 = 1.5. This z-score corresponds to a percentile of 93 on a z-score table. Therefore, the percentile for a redwood tree that is 375 feet tall is 93rd percentile. This means that 93% of redwood trees are shorter than 375 feet tall. It also means that only 7% of redwood trees are taller than 375 feet tall. This information can be used to compare the size of a particular redwood tree to other redwood trees.
Learn more about z score here
https://brainly.com/question/15016913
#SPJ4
Explain why the probability of rolling a sum from 2 to 12 is 100%. [C:2]
Answers
The probability of rolling a sum from 2 to 12 on 2 dices is 100%
Given the data,
The two dice should be rolled.
Now, there are 36 possibilities that might occur while rolling two normal six-sided dice. The reason for this is that when rolling two dice, the total number of outcomes is the product of the numbers of outcomes for each die, and each die has six potential outcomes (numbers 1 through 6).
The resultant 36 results are as follows:
1-1, 1-2, 1-3, 1-4, 1-5, 1-6
2-1, 2-2, 2-3, 2-4, 2-5, 2-6
3-1, 3-2, 3-3, 3-4, 3-5, 3-6
4-1, 4-2, 4-3, 4-4, 4-5, 4-6
5-1, 5-2, 5-3, 5-4, 5-5, 5-6
6-1, 6-2, 6-3, 6-4, 6-5, 6-6
When using two dice, there are a total of 36 possibilities that might occur.
As a result, the results' total ranges from 2 to 12.
Hence , the probability is 100 %
Click here for additional information about probability.
https://brainly.com/question/17089724
#SPJ1
Hep me on this please

Answers
Answer:
The answer is 2240m².
Step-by-step explanation:
Given that the formula of area of trapezium is A = 1/2×(a+b)×h where a and b represents the length and h is height :
\(area = \frac{1}{2} \times (a + b) \times h\)
\(let \: a = 50 \\ let \: b = 90 \\ let \: h = 32\)
\(area = \frac{1}{2} \times (50 + 90) \times 32\)
\(area = \frac{1}{2} \times 140 \times 32\)
\(area = 70 \times 32\)
\(area = 2240 \: {m}^{2} \)
Answer:
2,240 square meters
Step-by-step explanation:
The shape above is a trapezoid. Therefore, we can use the area formula for a trapezoid:
A=1/2(a+b) *h
where a is the short base, b is the long base is h is the height.
In this trapezoid, the short base is 50 meters , the long base is 90 meters and the height is 32 meters.
a= 50
b=90
h=32
A=1/2(50+90)*32
Add inside the parentheses first.
A=1/2(140)*32
Multiply 1/2 and 140, or divide 140 by 2.
A=70*32
Multiply 70 and 32
A=2240
Add appropriate units. In this case, the units are meters^2
A=2240 meters^2
The area of the playground is 2,240 meters^2
Talwar wants to invest R5800 at simple interest rate of 12,2% per annum. How many years will it take for the money to grow to R26100
Answers
It will take approximately 28.67 years for Talwar's investment of R5,800 to grow to R26,100 at a simple interest rate of 12.2% per annum.
To calculate the number of years it will take for Talwar's investment to grow to R26,100 at a simple interest rate of 12.2% per annum, we can use the formula for simple interest:
Simple Interest = Principal × Rate × Time
Given that the principal (P) is R5,800, the rate (R) is 12.2% (or 0.122 as a decimal), and the desired amount (A) is R26,100, we need to find the time (T) it will take. Rearranging the formula, we get:
Time = (Amount - Principal) / (Principal × Rate)
Plugging in the values, we have:
Time = (R26,100 - R5,800) / (R5,800 × 0.122)
= R20,300 / R708.6
≈ 28.67 years
For more such questions on investment
https://brainly.com/question/29227456
#SPJ8
need someone’s help with this please!!!
