Mary wants to buy a small fence place around us semi circular garden demeanor of a semi circle is 18 feet Mary calculus that she needs of about 28.3 feet of fence use a drop down menu to explain whether or not Mary's reasoning is correct use 3.4 for pie
Answers
Diameter of a semi circular garden = 18 feet
Radius of the garden :
\( = \tt\frac{diameter}{2} \)
\( =\tt \frac{18}{2} \)
\( =\tt 9 \: feet\)
Thus, the radius of the semi circular fence = 9 feet
We know that :
\(\color{hotpink}\tt \: Circumference \: of \:a \: semi \: circle \color{plum}=\pi r\)
Which means, the circumference of Mary's semi circular garden :
\( =\tt \pi r\)
(pi value = 3.14)
\( = \tt3.14 \times 9\)
\( =\tt 28.26 \: \: feet\)
Thus, the circumference of fence needed for the semi circular garden = 28.26 feet
28.26 can be rounded off to 28.30 and 28.30 is the same as 28.3
Thus, Mary's reasoning is correct.
Therefore, Mary's reasoning is correct which means she needs 28.3 feet of fence to surround her garden.
Related Questions
The coordinate grid shows a larger trapezoid and it’s smaller image after a dilation with a scale factor of 1/2
Answers
Answer:
1 and half
Step-by-step explanation:
this is a factor scale
Answer:
Step-by-step explanation:
Matthew is flying with his jet pack at 100m/min. A strong wind has blown him 10m east of his intended flight path in 2 minutes. By how many degrees is Matthew off his flight path? Include a diagram.
Answers
Mathew's speed of 100 m/min, and the distance of 10 m. east to which he is blown by the wind gives the angle in degrees Mathew is blown off his path as approximately 2.86°.
How can the angle of deflection be found from the given speeds?The given parameters are;
Speed at which Mathew is flying = 100 m/min
Distance and direction in which the strong wind blows him = 10 m. east
Time it takes the wind to deflect Mathew by 10 m. = 2 minutes
Therefore;
Speed and direction of the wind = 10/2 m/min east
Speed and direction of the wind = 5 m/min east
Mathew's flight path can be represented using a vector diagram (please see attached drawing)
Distance Mathew travels in 2 minutes = 100 m/min × 2 minutes = 200 m.
Tangent of the angle by which Mathew is off his flight path, A, can be found as follows;
tan(A) = 10/200 = 1/20
A = arctan(1/20) ≈ 2.86°Learn more about vectors here:
https://brainly.com/question/13432276
#SPJ1

What’s the answer ??

Answers
Fill in the table using this function rule
Y=2x+2
Answers
According to the equation, values of "Y" in the table would be 10 if X is 4 ; 12 if X is 5 ; 18 if X is 8 and 20 if X is 9.
As given equation is "Y=2x+2"
According to the table, we will put values of X in the equation to find the value of Y.
When X = 4,
Y = 2×4 + 2
Y = 10
When X = 5
Y = 2×5 + 2
Y = 12
When X = 8
Y = 2×8 + 2
Y = 18
When X = 9
Y = 2×9 + 2
Y = 20
Therefore values of Y would be 10, 12, 18, and 20 when X is 4, 5, 8, and 9 Respectively.
Visit here to learn more about the equation: https://brainly.com/question/10413253
#SPJ4
—------------- CORRECT QUESTION FORMAT IS GIVEN BELOW —-----------
(Q). Fill in the blank using this function Y=2x+2.
(Table is given below as in image section)

The length, breadth and total surface area of cuboid are 12 CM 10 CM and 592 CMsquare respectively find the height of the cuboid
Answers
The height of the cuboid is 8 cm. Answer: The height of the cuboid is 8 cm.
Let the height of the cuboid be h cm. Then, given that:Length of the cuboid = 12 cmBreadth of the cuboid = 10 cmTotal surface area of the cuboid = 592 cm²The total surface area of a cuboid is given by:Total surface area of a cuboid = 2(lb + bh + hl)Here, l = 12 cm, b = 10 cm and the total surface area of the cuboid is given as 592 cm².Thus, we have:592 = 2(12 × 10 + 10h + 12h)592 = 2(120 + 22h)592 = 240 + 44h352 = 44h8 = hh = 8
Therefore, the height of the cuboid is 8 cm. Answer: The height of the cuboid is 8 cm.
To know more about cuboid visit:-
https://brainly.com/question/29568631
#SPJ11
In 2019, selected automobiles had an average cost of $15,000. The average cost of those same automobiles is now $17,400. What was the rate of increase for these automobiles between the two time periods? (Enter your answer as a percentage, rounded to the neorest whole number.)
Answers
This means that the average cost of selected automobiles has increased by 16% between the two years.
Given data: The average cost of selected automobiles in 2019 = $15,000
The average cost of selected automobiles now (current year) = $17,400
Let's calculate the rate of increase in the average cost of the automobile between the two years.
To find the rate of increase, use the following formula;
rate of increase = increase in value / original value * 100
To get the increase in the value of selected automobiles, subtract the current year's average cost of selected automobiles from the previous year's average cost of selected automobiles.
i.e. increase in value = current year's average cost - previous year's average cost
= $17,400 - $15,000
= $2,400
Now put the values in the formula to get the rate of increase;
rate of increase = increase in value / original value * 100
= 2400 / 15000 * 100
= 16
Therefore, the rate of increase for selected automobiles between the two time periods is 16%.
It's essential to note the rate of increase or decrease in the value of products or services. It helps in decision making, future predictions, etc.
The above question deals with finding the rate of increase in the cost of selected automobiles. To get the rate of increase, the formula rate of increase = increase in value / original value * 100 is used.
To get the increase in the value of selected automobiles, subtract the current year's average cost of selected automobiles from the previous year's average cost of selected automobiles. i.e. increase in value = current year's average cost - previous year's average cost.
The value of selected automobiles was $15,000 in 2019, and now it is $17,400.
Now, the rate of increase in the average cost of automobiles can be found using the formula rate of increase = increase in value / original value * 100.
Put the values in the formula to get the rate of increase.
Therefore, the rate of increase for selected automobiles between the two time periods is 16%.
It indicates that if a person had bought an automobile in 2019 for $15,000, he has to pay $17,400 for the same automobile now.
To know more about percentage visit:
https://brainly.com/question/32197511
#SPJ11
(a) how many paths are there from the point (0, 0) to the point (110, 111) in the plane such that each step either consists of going one unit up or one unit to the right? (b) how many paths are there from (0,0) to (210, 211), where each step consists of going one unit up or one unit to the right, and the path has to go through (110, 111)?
Answers
(a) The number of pathways in the plane from point (0, 0) to point (110, 111) when each step consists of walking one unit up or one unit to the right is known as the number of ways to go to a point in a grid using just right and up moves.
This is a classic combinatorial problem known as a binomial coefficient. The binomial coefficient C(110+111, 110) = C(221, 110) = 221!/(110!111!) is the number of ways to travel from (0, 0) to (110, 111).
(b) The number of paths from (0, 0) to (210, 111) where each step consists of walking one unit up or one unit to the right and the path must pass through (110, 111) is the product of two binomial coefficients.
First, as calculated in section 1, the number of pathways from (0, 0) to (110, 111) is C(110+111, 110) = C(221, 110). Second, there are C(210+211, 210) ways to get from (110, 111) to (210, 111). (210, 211). (421, 210). C(221, 110) * C is the total number of paths found by multiplying these two binomial coefficients (421, 210).
To learn more about Binomial coefficients:
https://brainly.com/question/14216809
https://brainly.com/question/23478253
#SPJ4
Julisa had a coupon for 15% discount off the regular price of a pair of shoes at the stores. The regular price of the shoes she bought was $38.95. What was the discounted price of the shoes not including tax?
Answers
Answer:
33.10
Step-by-step explanation:
Help pleasee want asap

Answers
Answer:
I'm pretty sure it is D since all the other ones are maximum value parabolas (and the questions asks for a minimum) other than D.
Which inequality is true when the value of w is -3?
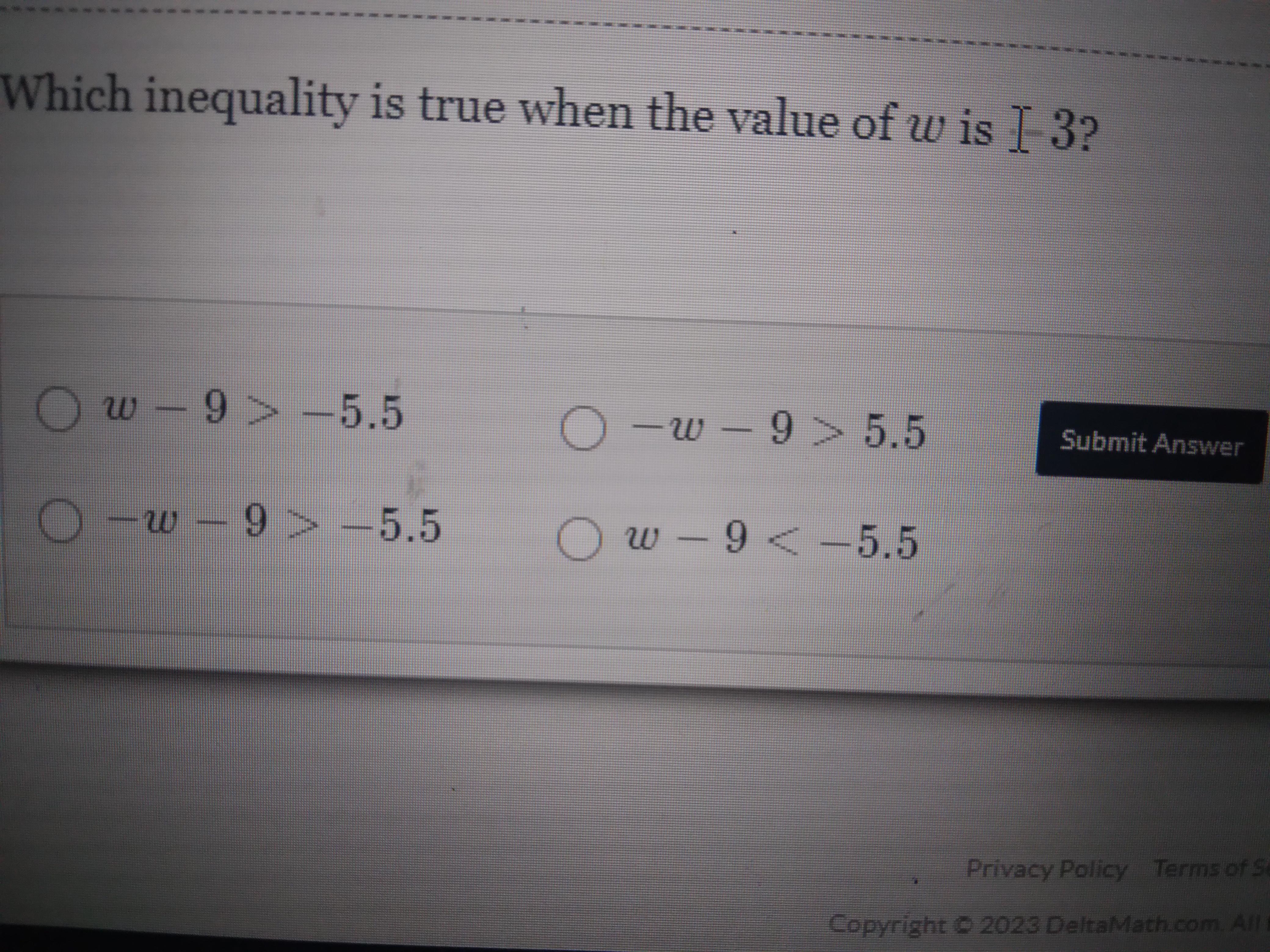
Answers
-3-9 = 12
12>5.5
Therefore this equation is true. The others are false. Hope this helps you:)
Make an input-output table for the function y = 2x + 4. Use x-values of 1, 2, 3, 4, and 5. Input, x 1 2. 3 4 5 Output, y5 Input, x 1 2 Output, y6 8 10 12 14 2 3 4 5 Input, x 1 Output, y6 36 76 156 Input, x 1 2 3 5 Output, y5 7 8

Answers
option B
Explanation:Function: y = 2x + 4
let the inputs for x = 1, 2, 3, 4, 5
To get the outputs, we insert each of the inputs:
when x = 1
y = 2(1) + 4 = 2 + 4
y = 6
when x = 2
y = 2(2) + 4 = 4 + 4
y = 8
when x = 3
y = 2(3) + 4 = 6 + 4
y = 10
when x = 4
y = 2(4) + 4 = 8 + 4
y = 12
when x = 5
y = 2(5) + 4 = 10 + 4
y = 14
The output values are: 6, 8, 10, 12, 14
The input -output table for the function is option B
HELP THIS IS DUE TONIGHT!!
What is the LCM (least common multiple) of the following
16ab^3 5a^2b^2 20ac
Also ^ means that it’s an exponent
Answers

I need help please it’s my hrw

Answers
Answer:
Blank 1: 28
Blank 2: 42
Blank 3: 22
Answer: It will take 7 sessions.
Step-by-step explanation:
We already know the 3 blanks from the equation 28x = 42 + 22x
Now to find the answer.
28x = 42 + 22x
Subtract 22x from both sides. This cancels the +22x.
28x - 22x = 42
Subtract 22x from 28x to get 6x
6x = 42
Divide both sides by 6. This undoes the multiplication by 6.
x = 42/6
Divide 42 by 6 to get 7.
x = 7
It will take 7 sessions for the costs to match.
Answer:
[28], [42], [22], the meet at 154 sessions
Step-by-step explanation:
Find the slope of each line. Tell whether the slop is Positive, Negative, Undefined or Zero

Answers
Because the line crosses at the y axis and you would have to find another line that’s right on the corner of a square, so you divide 1 and 1 and it’s 1
PLSSSSS HELP ME, Write a formula for the sum of the first three terms, a1+a2+a3, Your answer should only include variables a1 and d.
btw,
term 1=a1
common difference=d
Answers
Trying to get the right number possible. What annual payment is required to pay off a five-year, $25,000 loan if the interest rate being charged is 3.50 percent EAR? (Do not round intermediate calculations. Round the final answer to 2 decimal places.Enter the answer in dollars. Omit $sign in your response.) What is the annualrequirement?
Answers
To calculate the annual payment required to pay off a five-year, $25,000 loan at an interest rate of 3.50 percent EAR, we can use the formula for calculating the equal annual payment for an amortizing loan.
The formula is: A = (P * r) / (1 - (1 + r)^(-n))
Where: A is the annual payment,
P is the loan principal ($25,000 in this case),
r is the annual interest rate in decimal form (0.035),
n is the number of years (5 in this case).
Substituting the given values into the formula, we have:
A = (25,000 * 0.035) / (1 - (1 + 0.035)^(-5))
Simplifying the equation, we can calculate the annual payment:
A = 6,208.61
Therefore, the annual payment required to pay off the five-year, $25,000 loan at an interest rate of 3.50 percent EAR is $6,208.61.
Learn more about loan here: brainly.com/question/32625768
#SPJ11
What is the slope of a line parallel to the line whose equation is 12x+2y=24
Answers
Answer:
Step-by-step explanation:
The slope is 12 since the formula is y=mx+c
when m is representing the gradient or slope
Find the value of x:

Answers
Answer: 62 degrees
Step-by-step explanation:
For any triangle, the sum of the angles is equal to 180. So, if we look at the only triangle we have, we see that we have two angles given to us:
86 and 42 and then a third unknown angle, lets call it Z
Now how does this relate to the angle we need to find, or angle X? If we look at its location, angle (X) along with angle (Z) and angle 66 form a straight angle, this angle will come to measure 180 degrees. So looking at the information we found out, the only way to find Angle (X) is through finding out what angle (Z) measures, and that should be easy because we now know how to find angle (Z).
So to find angle Z we do:
180 = 86 + 42 + Z
now we need Z alone so we subtract both the 86 and 42 from both sides.
we are left with Z = 52
Now we use this to calculate angle (X)
So:
180 = 66 + Z + X
plug in what we know, Z = 52
we now have 180 = 66 + 52 + X
now again we want X alone so we subtract both 66 and 52 from both sides
we are left with X = 62
determine whether the series is absolutely convergent, conditionally convergent, or divergent. [infinity] sin(8n) 6n n = 1
Answers
The series is absolutely convergent.
To determine if the series is absolutely convergent, conditionally convergent, or divergent, we first analyze the absolute value of the series. We consider the series Σ|sin(8n)/6n| from n=1 to infinity. Using the comparison test
since |sin(8n)| ≤ 1, the series is bounded by Σ|1/6n| which is a convergent p-series with p>1 (p=2 in this case).
Since the series Σ|sin(8n)/6n| converges, the original series Σsin(8n)/6n is absolutely convergent. Absolute convergence implies convergence,
To learn more about : series
https://brainly.com/question/24644930
#SPJ11
The series sin(8n)/(6n) is divergent (by comparison with the harmonic series), the original series is not convergent.
To determine the convergence of the given series, we need to analyze it using the given terms. The series is:
Σ(sin(8n) / 6n) from n = 1 to infinity.
First, let's check for absolute convergence by taking the absolute value of the series terms: Lim m as n approaches infinity of |(sin(8(n+1))/(6(n+1))) / (sin(8n)/(6n))|
= lim as n approaches infinity of |(sin(8(n+1))/(6(n+1))) * (6n/sin(8n))|
= lim as n approaches infinity of |sin(8(n+1))/sin(8n)|
Σ|sin(8n) / 6n| from n = 1 to infinity.
Since |sin(8n)| is bounded between 0 and 1, we have:
Σ|sin(8n) / 6n| ≤ Σ(1 / 6n) from n = 1 to infinity.
Now, the series Σ(1 / 6n) is a geometric series with a common ratio of 1/6, which is less than 1. Therefore, this geometric series is convergent. By the comparison test, since the original series has terms that are less than or equal to the terms in a convergent series, the original series must be convergent.
In summary, the given series Σ(sin(8n) / 6n) from n = 1 to infinity is convergent.
Learn more about the series:
brainly.com/question/15415793
#SPJ11
You borrow $30,000 to buy a car. The loan is to be paid off in 10 equal quarterly payments at 6% interest annual interest rate. The first payment is due one quarter from today. What is the amount of each quarterly payment (rounded)? A. $1,777. B. $2,803. C. $3,253. D. None of the above.
Answers
The amount of each quarterly payment, rounded, for a $30,000 loan with a 6% annual interest rate to be paid off in 10 equal quarterly payments is $2,803 (option B).
To calculate the amount of each quarterly payment, we need to use the formula for calculating the equal payments on an installment loan. In this case, the loan amount is $30,000, the annual interest rate is 6%, and the loan term is 10 quarters.
Using the formula, we can determine that the amount of each quarterly payment is approximately $2,803. This amount is rounded to the nearest whole number, as specified in the question. Therefore, option B, $2,803, is the correct answer. The other options (A, C, and D) are not applicable to the calculation based on the given information.
Learn more about Whole number here: brainly.com/question/19161857
#SPJ11
You tie a spherical balloon that is 2 feet in diameter to a
stake in the ground. The string is 15 feet long. The wind
blows and you observe that the top of the balloon is
8 feet over from the stake, as shown in the diagram.
What is the height, b, of the balloon?
Show your work.
15 ft
2 ft
8 ft
Answers
Answer:
Step-by-step explanation:
To make a candle, you use a mold to create the wax pyramid shown. You cut off the top 3 centimeters of the
pyramid to make space for a wick. If the base area of the removed portion is 5.4 square centimeters, what percentage of the wax did you remove?
Answers
50% of the wax was removed to create space for the wick.
What is area?
A two-dimensional surface's area can be used to determine its size. It measures the volume of space a shape or other figure encloses. Square units are commonly used to express it.
What is percentage?
A fraction or percentage can be expressed as a percentage of 100 by using the word "percentage." "%" is used to represent it.
To calculate the percentage of wax that was removed, we need to compare the volume of the removed portion to the volume of the original pyramid.
Given:
Height of the original pyramid (H) = 6 centimeters
Base area of the removed portion = 5.4 square centimeters
To find the percentage of wax removed, we can use the following steps:
Calculate the volume of the original pyramid:
Original Volume = (1/3) * Base Area * Height
= (1/3) * 5.4 * 6
= 10.8 cubic centimeters
Calculate the volume of the removed portion:
Removed Volume = (1/3) * Base Area * Removed Height
= (1/3) * 5.4 * 3
= 5.4 cubic centimeters
Calculate the percentage of wax removed:
Percentage Removed = (Removed Volume / Original Volume) * 100
= (5.4 / 10.8) * 100
= 0.5 * 100
= 50%
Therefore, you have removed 50% of the wax to create space for the wick.
To learn more about area follow the given link:
https://brainly.com/question/27440983
#SPJ4
Ten pipes can drain a pool in 2 hours. if only 4 pipes are used, how
long will it drain the pool?
what kind of proportion is this , partitive , direct , or inverse
Answers
If only 4 pipes are used instead of ten, the time required to drain the pool can be determined by finding the proportion between the number of pipes and the time. It is an inverse proportion.
Let's assume the volume of the pool is represented by V. Since ten pipes can drain the pool in 2 hours, it means that each pipe can drain 1/10th of the pool's volume in 2 hours. Therefore, the rate at which each pipe drains the pool is (1/10)V per 2 hours.
Now, if we only use 4 pipes instead of 10, the rate at which the pool will be drained will decrease. Let's represent the time it takes to drain the pool with 4 pipes as T.
Using the idea of an inverse proportion, we can set up the following equation:
(1/10)V / 2 hours = (1/4)V / T
To solve for T, we can cross-multiply and simplify:
T = 2 hours * (4/10)
T = 0.8 hours
Therefore, if only 4 pipes are used instead of 10, it will take 0.8 hours (or 48 minutes) to drain the pool.
In conclusion, the relationship between the number of pipes and the time taken to drain the pool is an inverse proportion. As the number of pipes decreases, the time required to drain the pool increases.
To learn more about pipes -
brainly.com/question/29172882
#SPJ11
A stores average daily sales during its first year in 1991 were $345. Since the the average daily sales have increased by about $35 each year. Let t be the number of years since 1991. Which equation represents the average daily sales as a function of t?
Answers
The expression that represents the average daily sales as a function of t will be 345 + 35t
How to illustrate the expression?In Mathematics, it is important to note that an expression is simply used to show the relationship between the variables that are provided or the data given regarding an information.
Since the stores average daily sales during its first year in 1991 were $345. Since the the average daily sales have increased by about $35 each year.
Let t be the number of years since 1991.
The equation represents the average daily sales as a function of t will be:
345 + (35 × t)
= 345 + 35t
Learn more about expressions on
brainly.com/question/723406
#SPJ1
PLEASE I NEED HELP AND EXPLAIN PLZ

Answers
Answer:
Statement:
1. C
2. A
3. B
Reason:
1. F
2. E
3. H
Step-by-step explanation:
C is very clearly the given so it goes first and B is what you're trying to prove so that goes last
Hope this helped <3
help me!
solve for y

Answers
Answer:
\sqrt{7}i or -\sqrt{7}i
Step-by-step explanation:
square root both sides of the equation
since you can't sqrt a negative number, you substitute sqrt of -1 to i
Which gets the answer.
How to form a polynomial with given zeros and degree?
Answers
To form a polynomial with given zeros and degree, we need to use the fact that if a polynomial has a zero of x = a, then it can be factored as (x - a) times some other polynomial.
This means that if we know the zeros of a polynomial, we can write it in factored form, and then multiply out the factors to get the polynomial in standard form.
The degree of the polynomial tells us how many factors are necessary. For example, if the degree is 3, we know that the polynomial can be factored into three linear factors, one for each zero.
To illustrate this process, let's say we want to form a polynomial of degree 4 with zeros of x = 2, x = -1, and x = 3. We would start by writing the polynomial in factored form as:
f(x) = (x - 2)(x + 1)(x - 3)(ax + b)
Since the degree is 4, we need to include one more factor. We can use the coefficients a and b to determine this factor. To do so, we can either use the value of the leading coefficient (which is a in this case) or a point on the polynomial (i.e., a value of x and f(x)).
Once we have determined the value of a, we can solve for b by setting a point on the polynomial equal to a known value.
Finally, we can multiply out the factors to get the polynomial in standard form:
f(x) = (x - 2)(x + 1)(x - 3)(2x - 4)
f(x) = 2x^4 - 8x^3 - 13x^2 + 22x - 12
In conclusion, to form a polynomial with given zeros and degree, we need to use the fact that a polynomial can be factored as (x - a) times some other polynomial if it has a zero of x = a.
We can write the polynomial in factored form, determine the missing factor(s) using the degree and coefficients, and then multiply out the factors to get the polynomial in standard form.
To learn more about polynomial click on,
https://brainly.com/question/14742650
#SPJ4
HURRY PLEASE!! What is the solution to the system of equations?
x -5=y
x+y=4
A (18, 1)
B (9/2, -7/2)
C (-2, 17/3)
Answers
Answer:
(9/2, -1/2)
Step-by-step explanation:
solve for the missing sidebof the triangle shown in the figure

Answers
Answer:
∠B = 74°
a ≈ 14.5 inches
c ≈ 11.4 inches
Step-by-step explanation:
The given parameters of triangle ΔABC are;
∠A = 62.2°, ∠C = 43.8° and side \(\overline{AB}\) = b = 15.8 in
By sine rule, we have;
\(\dfrac{a}{sin(\angle A)} = \dfrac{b}{sin(\angle B)} = \dfrac{c}{sin(\angle C)}\)
\(a = {sin(\angle A)} \times \dfrac{b}{sin(\angle B)}\)
By angle sum property, we have;
∠B = 180° - (∠A + ∠C)
∴ ∠B = 180° - (62.2° + 43.8°) = 74°
∠B = 74°
\(\therefore {a} = {sin(62.2^{\circ})} \times \dfrac{15.8}{sin(74^{\circ})} \approx 14.5\)
a ≈ 14.5 in.
\(c = {sin(\angle C)} \times \dfrac{b}{sin(\angle B)}\)
\(\therefore {c} = {sin(43.8^{\circ})} \times \dfrac{15.8}{sin(74^{\circ})} \approx 11.4\)
c ≈ 11.4 in.
The length of a rectangle is 5 units more than the width. The area of the rectangle is 36 square units. What is the length, in units, of the rectangle?
Answers
Answer:
The length is 9 units
Step-by-step explanation:
Lenght is 9, width is 4,
9 x 4 = 36
Answer:
The length of the rectangle is 9 units
Step-by-step explanation:
1. Write down what we know:
Area of rectangle = L x WL = W + 5Area = 362. Write down all the ways we can get 36 and the difference between the two numbers:
36 x 1 (35)18 x 2 (16)12 x 3 (9)9 x 4 (5)6 x 6 (0)3. Find the right one:
9 x 4 = 36The difference between 9 and 4 is 5Hence the answer is 9 units