Marsha recorded the time it took seven children of different ages to run one lap around the track.
Using the line of best fit, which is closest to the length of time it should take Marsha's 6 year old niece to
run one lap?
A. 190
B. 200
C. 205
D. 210

Answers
Reasoning: There is a 40s difference between the age of 4 and 8 meaning 6 most likely would be in the center of that, which also means it’d be about half of 40. So with that we subtract 20 from 225 and thus giving us the closest length of time it should take Marsha’s 6 year old niece to run one lap, 205s.
Related Questions
What subtraction sentence does this show?
A. 4.3 - (-0.9) = 5.2
B. 4.3 - 0.9 = 5.2
C. -4.3 - 0.9 = 5.2
D. -4.3 - (-0.9) = 5.2
What is the solution to this addition sentence?
3/4 + (-1/2) = _____
A. -5/4
B. -1/4
C. 1/4
D. 5/4
What is 2/3 – (-2/3)?
A. -4/3
B. 4/3
C. 0
D. 2/3
What is the sum of 2/5 and -4/5?
A. -4/5
B. -2/5
C. 2/5
D. 4/5
What is 4 – (-6)?
A. -10
B. -2
C. 2
D. 10
What is the sum of -2/6 and 3/2?
A. -11/6
B. -7/6
C. 7/6
D. 11/6
What addition sentence does this show?
A.
B.
C.
D.
What is the solution to this subtraction sentence?
3/4 – (-1/4) = ________
A. -1
B. -1/2
C. 1/2
D. 1
What addition statement does this show?
A. -3.4 + 5.7 = -9.1
B. -3.4 + (-5.7) = -9.1
C. 3.4 + (-5.7) = -9.1
D. 3.4 + 5.7 = -9.1
just give the answers
Answers
Answer:
1. b 2. d 3 a
Step-by-step explanation:
Subtracting from the group or a number of things is what subtracting signifies in math, and the calculation can be defined as follows:
Subtraction calculation:Following are the solution to the given subtraction equations:
For question 1:
A) 4.3 - (-0.9) = 4.3+ 0.9= 5.2 that is true
B) 4.3 - 0.9 = 5.2 that is false because answer is 3.4
C) -4.3 - 0.9 = 5.2 that is false because answer is -5.2
D) -4.3 - (-0.9) = -4.3 +0.9 = 5.2 that is false because answer is -3.4
For question 2:
\(\to \frac{3}{4} + (-\frac{1}{2})\\\\\to \frac{3}{4} -\frac{1}{2}\\\\\to \frac{3-2}{4}\\\\\to \frac{1}{4}\\\\\)
Therefore, the answer is "Option C".
For question 3:
\(\to \frac{2}{3} - (-\frac{2}{3})\\\\\to \frac{2}{3} +\frac{2}{3}\\\\\to \frac{4}{3}\\\\\)
Therefore, the answer is "Option B".
For question 4:
\(\to \frac{2}{5} + (-\frac{4}{5})\\\\\to \frac{2}{5} -\frac{4}{5}\\\\\to \frac{2-4}{5}\\\\\to \frac{-2}{5}\\\\\)
Therefore, the answer is "Option B".
For question 5:
\(\to\) 4 – (-6)
\(\to\) 4 +6
\(\to\) 10
Therefore, the answer is "Option D".
For question 6:
\(\to - \frac{2}{6} + (\frac{3}{2})\\\\\to - \frac{1}{3} + \frac{3}{2}\\\\\to \frac{2-9}{6}\\\\\to \frac{-7}{6}\\\\\)
Therefore, the answer is "Option B".
For question 8:
\(\to \frac{3}{4} - (-\frac{1}{4})\\\\\to - \frac{3}{4} + \frac{1}{4}\\\\\to \frac{3+1}{4}\\\\\to \frac{4}{4} \\\\ \to 1\)
Therefore, the answer is "Option D".
For question 9:
A) -3.4 + 5.7 = -9.1 that's is false because answer is 2.3
B) -3.4 + (-5.7) = -9.1 that's is true.
C) 3.4 + (-5.7) = -9.1 that's is false because answer is -2.3
D) 3.4 + 5.7 = -9.1 that's is false because answer is 9.1
Find out more about the subtraction here:
brainly.com/question/1927340
In the given figure ABCD, prove that
angleBCD= angleBAD+ angle ABC+angle ADC.
[Hint: Join A and C then extended AC to the point E]

Answers
We have proved that Angle BCD is equal to angle BAD plus angle ABC plus angle ADC, as required.
To prove that angle BCD is equal to angle BAD plus angle ABC plus angle ADC, we can use the following steps:
Step 1: Join points A and C with a line segment. Let's label the point where AC intersects with line segment BD as point E.
Step 2: Since line segment AC is drawn, we can consider triangle ABC and triangle ADC separately.
Step 3: In triangle ABC, we have angle B + angle ABC + angle BCA = 180 degrees (due to the sum of angles in a triangle).
Step 4: In triangle ADC, we have angle D + angle ADC + angle CDA = 180 degrees.
Step 5: From steps 3 and 4, we can deduce that angle B + angle ABC + angle BCA + angle D + angle ADC + angle CDA = 360 degrees (by adding the equations from steps 3 and 4).
Step 6: Consider quadrilateral ABED. The sum of angles in a quadrilateral is 360 degrees.
Step 7: In quadrilateral ABED, we have angle BAD + angle ABC + angle BCD + angle CDA = 360 degrees.
Step 8: Comparing steps 5 and 7, we can conclude that angle B + angle BCD + angle D = angle BAD + angle ABC + angle ADC.
Step 9: Rearranging step 8, we get angle BCD = angle BAD + angle ABC + angle ADC.
Therefore, we have proved that angle BCD is equal to angle BAD plus angle ABC plus angle ADC, as required.
For more questions on Angle .
https://brainly.com/question/31615777
#SPJ8
Given: Quadrilateral \(\displaystyle\sf ABCD\)
To prove: \(\displaystyle\sf \angle BCD = \angle BAD + \angle ABC + \angle ADC\)
Proof:
1. Draw segment \(\displaystyle\sf AC\) and extend it to point \(\displaystyle\sf E\).
2. Consider triangle \(\displaystyle\sf ACD\) and triangle \(\displaystyle\sf BCE\).
3. In triangle \(\displaystyle\sf ACD\):
- \(\displaystyle\sf \angle ACD = \angle BAD + \angle ADC\) (Angles of a triangle add up to \(\displaystyle\sf 180^\circ\)).4. In triangle \(\displaystyle\sf BCE\):
- \(\displaystyle\sf \angle BCE = \angle BAD + \angle ABC\) (Angles of a triangle add up to \(\displaystyle\sf 180^\circ\)).5. Since \(\displaystyle\sf \angle BCE\) and \(\displaystyle\sf \angle BCD\) are corresponding angles formed by transversal \(\displaystyle\sf BE\):
- \(\displaystyle\sf \angle BCE = \angle BCD\).6. Combining the equations from steps 3 and 4:
- \(\displaystyle\sf \angle BCD = \angle ACD = \angle BAD + \angle ADC\). - \(\displaystyle\sf \angle BCD = \angle BCE = \angle BAD + \angle ABC + \angle ADC\).Therefore, we have proven that in quadrilateral \(\displaystyle\sf ABCD\), \(\displaystyle\sf \angle BCD = \angle BAD + \angle ABC + \angle ADC\).
\(\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}\)
♥️ \(\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}\)
An external force F(t) = 2cos 2t is applied to a mass- spring system with m = 1 b = 0 and k = 4 which is initially at rest; i.e., y(0) = 0 y' * (0) = 0 Verify that y(t) = 1/2 * t * sin 2t gives the motion of this spring. What will eventually (as t increases) happen to the spring?
Answers
To verify that y(t) = (1/2) * t * sin(2t) represents the motion of the spring, we need to find the second derivative of y(t) and substitute it into the equation of motion for the mass-spring system. Answer : the spring will experience increasingly larger oscillations as time goes on.
The equation of motion for a mass-spring system is given by:
m * y''(t) + b * y'(t) + k * y(t) = F(t),
where m is the mass, b is the damping coefficient, k is the spring constant, y(t) represents the displacement of the mass from its equilibrium position, and F(t) is the external force.
In this case, m = 1, b = 0, k = 4, and F(t) = 2 * cos(2t). The initial conditions are y(0) = 0 and y'(0) = 0.
Let's calculate the second derivative of y(t):
y(t) = (1/2) * t * sin(2t)
y'(t) = (1/2) * (sin(2t) + 2t * cos(2t))
y''(t) = (1/2) * (2cos(2t) + 2cos(2t) - 4t * sin(2t))
= cos(2t) - 2t * sin(2t)
Now, substitute y(t), y'(t), and y''(t) into the equation of motion:
m * y''(t) + b * y'(t) + k * y(t) = F(t)
1 * (cos(2t) - 2t * sin(2t)) + 0 * ((1/2) * (sin(2t) + 2t * cos(2t))) + 4 * ((1/2) * t * sin(2t)) = 2 * cos(2t)
Simplifying the equation:
cos(2t) - 2t * sin(2t) + 2t * sin(2t) = 2 * cos(2t)
cos(2t) = 2 * cos(2t)
The equation holds true for all values of t.
Since the equation of motion is satisfied by y(t) = (1/2) * t * sin(2t) and the initial conditions are also satisfied, we can conclude that y(t) = (1/2) * t * sin(2t) represents the motion of the spring.
Now, let's discuss what will eventually happen to the spring as t increases. In this case, the spring is undamped (b = 0) and the system is driven by an external force F(t) = 2 * cos(2t). The motion of the spring is given by the function y(t) = (1/2) * t * sin(2t).
As t increases, the displacement of the spring (y(t)) will continue to oscillate. The amplitude of the oscillation will grow unbounded, as there is no damping to counteract the energy being input by the external force. Therefore, the spring will experience increasingly larger oscillations as time goes on.
Learn more about force : brainly.com/question/13191643
#SPJ11
The expression, (5 > 57 % 8), evaluates to ____. true false
Answers
The expression, (5 > 57 % 8), evaluates to false.
To determine if the expression (5 > 57 % 8) evaluates to true or false, we need to first calculate the value of 57 % 8.
Step 1: Calculate 57 % 8, which represents the remainder when 57 is divided by 8.
57 % 8 = 1
Step 2: Compare 5 and the result from Step 1 using the '>' operator.
5 > 1
Step 3: Determine if the comparison in Step 2 is true or false.
Since 5 is greater than 1, the expression evaluates to true.
So, the expression (5 > 57 % 8) evaluates to true.
Learn more about expression:
brainly.com/question/14083225
#SPJ11
Kate ran 4 miles. How far did she run in kilometers?
Answers
Answer:
About 6.44 kilometers
Step-by-step explanation:
I mile is approximately 1.61 kilometers, so 4 miles would be 1.61 · 4 = 6.44 kilometers.
Hope this helps!
Which linear function has the same slope as the one that is represented by the table?
X Y
-1/2 1/5
-1/5 7/50
1/5 3/50
1/2 0
A).y=1/2x+1/10
B).y=-1/5x+1/10
C).y=1/5x-1/2
D).y=1/2x-1/10
Answers
Option B's equation y = -1/5x + 1/10 has the same slope as the linear function depicted in the table.
What does linear function mean?One way to describe a linear function is as an algebraic equation with variables raised to the power .A straight line makes up the graph of a linear equation. Y = mx + b, where x and y are variables and m and b are constants, is one of the most typical examples of a linear function.
For instance, if we have the linear function f(x) = 2x + 3, we may calculate the value of f(4) by changing x to 4 and getting f(4) = 2(4) + 3 = 11.
Calculating the difference between y and x for any two points will allow us to determine the slope of the linear function shown in the table. Let's pick the first and last items from the table:
Slope = (change in y) / (change in x) = (0-1/5) / (1/2 - (-1/2)) = (-1/5) / 1 = -1/5
As a result, the table's linear function has a slope of -1/5.
The next step is to find the linear function whose slope is equal to -1/5. Let's look at the possibilities:
A) y = 1/2x + 1/10, slope = 1/2; B) y = -1/5x + 1/10, slope = -1/5 (correct)
C) y = 1/5x - 1/2, slope = 1/5; D) y = 1/2x - 1/10, slope = 1/2
As a result, option B, y = -1/5x + 1/10, is the linear function with the same slope as the one shown in the table.
To know more about linear function visit:
https://brainly.com/question/14695009
#SPJ1
The linear function with the same slope as the one represented by the table is: y = -1/5x + 1/10
So the answer is B) y = -1/5x + 1/10.
What is linear function?A linear function is a mathematical function that has a graph that is a straight line.
It can be represented by the equation y = mx + b, where x and y are variables, m is the slope of the line, and b is the y-intercept.
To find the slope of the linear function represented by the given table, we can choose any two points and use the slope formula:
slope = (change in y) / (change in x)
Let's choose the points (-1/2, 1/5) and (1/2, 0):
slope = (0 - 1/5) / (1/2 - (-1/2))
= (-1/5) / 1
= -1/5
So the slope of the linear function is -1/5.
Now we need to find the linear function with the same slope.
The general form of a linear function is y = mx + b, where m is the slope and b is the y-intercept. We know that the slope is -1/5, so we can eliminate answer choices A and D, which have slopes of 1/2 and 1/2, respectively.
To determine the y-intercept, we can use one of the points from the table. Let's use the point (-1/2, 1/5):
1/5 = (-1/5)(-1/2) + b
Simplifying:
1/5 = 1/10 + b
b = 1/5 - 1/10
b = 1/10
So the y-intercept is 1/10.
To know more about slope visit:
https://brainly.com/question/13407962
#SPJ1
An agent is listing a 2 story property which measures 26’X28’. Comparable properties are selling for $143 dollars per square foot plus $54,350 land. What is the value of the listing?
Answers
Multiply this result by two (it's a 2-story house); then, multiply it by the cost per square foot and add the land cost.
\(\begin{gathered} V=2\cdot728\cdot143+54350 \\ \Rightarrow V=262558 \end{gathered}\)Then, the value of the listing is $262558
true or false: if event a is tina is the first woman to finish the 2020 boston marathon and event b is tina is the first woman to finish the 2021 new york marathon, event a and event b are independent.
Answers
It is true that the events a and b, relating to Tina being the first woman to finish the 2020 Boston Marathon and the 2021 New York Marathon, are independent.
What are independent events?Independent events are events where the occurrence or non-occurrence of one event does not affect the probability of the occurrence or non-occurrence of the other event. In other words, the outcome of one event has no impact on the outcome of the other event.
In the context of this problem, the outcome of one marathon has no bearing on the outcome of another marathon, hence it is true that the events a and b are independent.
More can be learned about independent events at https://brainly.com/question/22881926
#SPJ1
I need help in this question

Answers
Answer:
a) £105 300
b) £132 300
Step-by-step explanation:
a) 2700*39=105 300
b) 2700*49=132 300
x=x property of equality
Answers
Answer:
Reflexive Property
Step-by-step explanation:
For all real numbers x , x=x . A number equals itself
6 (4x6) x 9 (5x9) judjsjdjdjddjdnnddnfndndndndndndndndn
Answers
Answer:
48 600
Step-by-step explanation:
6(4×6) × 9(5×9)
Solve the numbers in brackets first
6(20) × 9(45)= 120 × 405
= 4 8 600
Answer:
6(20) × 9(45)= 120 × 405
= 4 8 600
is this correct (thank you and 5 stars)

Answers
Answer:
Correct!
Step-by-step explanation:
Good Job
Given: (↔AB) ║ (↔CD)
If the coordinates of point A are (8 , 0) and the coordinates of point B are (3 , 7), the y-intercept of (↔AB) is (?) . If the coordinates of point D are (5 , 5), the equation of line (↔CD) is y =(?) x +(?).
can someone please help me figure out what the (?) is.
Answers
y = mx + b
m = 7 - 0/3 - 8
y = -7/5x + 11.2
2) y= -7/5x + 12
(the slope or m stays the same because the two equations are parallel)
Answer:
1. 56/5
2. -7/5
3. 12
Step-by-step explanation:
The area of the parallelogram below is ____ square meters.
A parallelogram with height labeled with 8 meters. The top horizontal side is labeled 6 meters. The base of the left triangle formed by the height is 2 meters.
WILL GIVE BRAINLIST WHO EVER ANSWERS
Answers
Answer:
48 m²
Step-by-step explanation:
Given that:
Height of parallelogram, h = 8 meters
Base length of parallelogram, b = 6 meters
The Area of a parallelogram is given by :
Base * height
8 meters * 6 meters
= 48 m²
a) Solve the heat equation by the method of separation of variables. Show all the steps and logic. What is the meaning of u(x, t)? Ut=Uxx'
t>0, 0≤x≤1
ux(0,t)=0, u(1,t)=0, u(x,t)3Cos(7π/2 x)
Answers
The solution to Ut=Uxx is u(x,t) = ∑_(m=0)^∞▒〖A_(2m+1)cos((2m+1)πx) e^(-(2m+1)^2π^2t)〗 and u(x,t) is the temperature function of the rod.
The heat equation can be solved by the method of separation of variables by assuming the solution u(x, t) is of the form U(x)T(t).
Therefore, Ut = Uxx' can be transformed to (1/T)dT = (1/U)d^2U.
The left-hand side of the above equation is only a function of t, and the right-hand side is only a function of x.
Therefore, each side must be equal to a constant λ.
The equation (1/T)dT = λ dt has the solution T(t) = exp(λt).
The equation (1/U)d^2U = λ dx^2 has the solution U(x) = Asin(nπx) or Acos(nπx), where n is a positive integer.
The solution to Ut=Uxx is therefore u(x,t) = ∑_(n=1)^∞▒〖(A_ncos(nπx))e^(λ_n t)〗.
The values of A_n and λ_n must be determined using the boundary conditions, ux(0,t) = 0 implies that An = 0 for all n.
u(1,t) = 0 implies that Acos(nπ) = 0 for all n except n = 2m + 1, where m is a positive integer.
λ_n = -(nπ)^2.
Hence, the solution to Ut=Uxx is u(x,t) = ∑_(m=0)^∞▒〖A_(2m+1)cos((2m+1)πx) e^(-(2m+1)^2π^2t)〗.
u(x,t) represents the temperature of a rod that extends from x = 0 to x = 1 at time t.
The function u(x,t) is defined by the values of A_(2m+1) and determines the temperature at any point in the rod and at any time.
To know more about heat equation, visit
https://brainly.com/question/64223
#SPJ11
PLS HELP ME 50 POINTS PLSSSSSSSSSSSS
Percent Check
Find each number. Round to the nearest tenth if necessary.
1. 20% of 70
2. 28.2% of 92
3. 60% of 68 is what number?
4. 25% of 96 is what number?
Estimate.
5. 8% of 40
6. 24% of 60
Write an equation for each problem.
Then solve. Round to the nearest tenth if necessary.
7. What number is 8% of 50?
8. 52 is what percent of 260?
9. 30 is 75% of what number?
10. What is 15% of 24?
11. Tiffany answered 90% of the questions on her
math test correctly. There were 50 questions on
the test. How many questions did Tiffany
answer correctly?
12. Jerilyn made 40 treats for her birthday. She
gave 4 away to her family before taking the
rest to school. What percent did she give away
to her family?
Answers
Step-by-step explanation:
11 is she answered 40 questions correctly
Answer:
1. 0.2 x 70 = 14
2. 0.282 x 92 = 25.9
3. 0.6 x 68 = 40.8
4. 0.25 x 96 = 24
5. 0.08 x 40 = 3.2 = 3
6. 0.24 x 60 = 14.4 = 14
7. 0.08 x 50 = 4
8. 52 divided by 260 = 0.2 = 20%
9. 30 divided by 0.75 (75%) = 40
10. 0.15 x 24 = 3.6
11. 0.9 x 50 = 45
12. 4 divided by 40 = 0.1 = 10%
the weights of a large number of miniature poodles are approximately normally distributed with a mean of 8 kilograms and a standard deviation of 0.9 kilogram. if measurements are recorded to the nearest tenth of a kilogram, find the fraction of these poodles with weights (a) over 9.5 kilograms; (b) of at most 8.6 kilograms; (c) between 7.3 and 9.1 kilograms inclusive
Answers
(a) The fraction of poodles with weights over 9.5 kilograms is about 0.0475
(b) The fraction of poodles with weights of at most 8.6 kilograms is about 0.7486
(c) The fraction of poodles with weights between 7.3 and 9.1 kilograms inclusive is about 0.6488
We can solve this problem using the standard normal distribution, which has a mean of 0 and a standard deviation of 1. We'll first standardize the given values using the formula
z = (x - μ) / σ
where z is the standard score, x is the given value, μ is the mean, and σ is the standard deviation.
(a) To find the fraction of poodles with weights over 9.5 kilograms, we standardize 9.5 kg as follows
z = (9.5 - 8) / 0.9
z = 1.67
Using a standard normal distribution table or calculator, we find that the area to the right of z = 1.67 is approximately 0.0475. Therefore, the fraction of poodles with weights over 9.5 kg is about 0.0475
(b) To find the fraction of poodles with weights of at most 8.6 kilograms, we standardize 8.6 kg as follows
z = (8.6 - 8) / 0.9
z = 0.67
Using a standard normal distribution table or calculator, we find that the area to the left of z = 0.67 is approximately 0.7486. Therefore, the fraction of poodles with weights of at most 8.6 kg is about 0.7486 or 74.86%.
(c) To find the fraction of poodles with weights between 7.3 and 9.1 kilograms inclusive, we standardize both values
z1 = (7.3 - 8) / 0.9
z1 = -0.78
z2 = (9.1 - 8) / 0.9
z2 = 1.11
Using a standard normal distribution table or calculator, we find the area to the left of z1 is approximately 0.2177 and the area to the left of z2 is approximately 0.8665. Therefore, the area between z1 and z2 is
0.8665 - 0.2177 = 0.6488
Learn more about standard score here
brainly.com/question/13579780
#SPJ4
Which parameter is often associated with enzyme affinity for substrates? \( k_{1} \) \( k_{-1} \) \( k_{2} \) \( K_{m} \)
Answers
The parameter often associated with enzyme affinity for substrates is Km.
Km, also known as the Michaelis constant, is a parameter commonly used to quantify the affinity of an enzyme for its substrate. It is an important parameter in enzyme kinetics and plays a crucial role in determining the efficiency of an enzyme-substrate interaction.
Km represents the substrate concentration at which the rate of the enzymatic reaction is half of its maximum velocity (Vmax). In other words, enzymes with lower Km values have higher affinity for their substrates, as they can achieve half of their maximum velocity at lower substrate concentrations. Therefore, Km serves as an indicator of the enzyme's ability to bind and convert substrates into products efficiently.
Learn more about substrates here : brainly.com/question/6107295
#SPJ11
if
f(x)=|x-8|-(x-8), find f(2). write the equation of the line in
standard form and in slope intercept form ?
Determine the slope and the y intercept of the line.
-24=2y
find the x intercept and t
Answers
The equation of the line in standard form is Ax + By = C, where A, B, and C are constants. To write it in slope-intercept form, y = mx + b, where m is the slope and b is the y-intercept. The x-intercept is 12 and the y-intercept is 10.
To find f(2), we substitute x = 2 into the given function:
f(2) = |2-8| - (2-8)
= |-6| - (-6)
= 6 - (-6)
= 6 + 6
= 12
Therefore, f(2) = 12.
The equation of the line in standard form is Ax + By = C, where A, B, and C are constants. To write it in slope-intercept form, y = mx + b, where m is the slope and b is the y-intercept, we need to rearrange the equation.
-24 = 2y
Dividing both sides by 2:
-12 = y
The line intersects the y-axis at y = -12, so the y-intercept is -12.
To find the x-intercept and y-intercept of the equation x/6 + y/5 = 2, we set each variable to zero in turn.
When x = 0:
0/6 + y/5 = 2
y/5 = 2
y = 10
The y-intercept is y = 10.
When y = 0:
x/6 + 0/5 = 2
x/6 = 2
x = 12
The x-intercept is x = 12. Therefore, the x-intercept is 12 and the y-intercept is 10.
LEARN MORE ABOUT equation here: brainly.com/question/14686792
#SPJ11
COMPLETE QUESTION - if f(x)=|x-8|-(x-8), find f(2). write the equation of the line in standard form and in slope intercept form ? Determine the slope and the y intercept of the line. -24=2y find the x intercept and the y intercept x/6 + y/5 =2.
if you add 10 to every value of a data set, what happens to the standard deviation?
Answers
The standard deviation of the data set will increase by a factor of 10. This is because standard deviation measures how much variation or dispersion exists from the mean of a data set. Adding 10 to every value of the data set will increase the overall spread of the data and thus increase the standard deviation.
To prove this mathematically, let's consider a data set A with mean M and standard deviation SD. Let's add 10 to every value of the data set to get a new data set B. The mean of set B is M+10 and the standard deviation of set B is SD'. The formula for SD' is:
SD':\(\sqrt{(x_{1} -(M+10))^{2} +(x_{2} -(M+10))^2+ (x_{3}-(M+10))^2 +...+ (x_{n}-(M+10))^2)/n }\) We can simplify this by substituting the values for the xi:
SD' =\(\sqrt{(((x_{1}-M-10)^2 + (x_{2}-M-10)^2 + (x_{3}-M-10)^2 +...+ (x_{n}-M-10)^2)/n) }\) Now let's consider the original data set A and its standard deviation SD:
SD =\(\sqrt{(((x_{1}-M)^2 + (x_{2}-M)^2 + (x_{3}-M)^2 +...+ (x_{n}-M)^2)/n) }\) ,We can substitute the values for xi in this formula as well:
SD= \(\sqrt{ (((x_{1}-M-10)^2 + (x_{2}-M-10)^2 + (x_{3}-M-10)^2 +...+ (x_{n}-M-10)^2)/n)}\) If we compare SD and SD', we can see that they are identical, except that the value of M has been replaced with M+10. This means that when we add 10 to every value of the data set, the standard deviation increases by a factor of 10.
To know more about standard deviation refer to the link brainly.com/question/23907081
#SPJ4
find the value of 8s-5t when s=3 and t=-2
Answers
Answer:
34
Step-by-step explanation:
Substitute the values.
s = 3 and t = -2
8s-5t
8 (3) - 5(-2)
( 8 x 3 ) - ( 5 x -2 )
24 + 10 [ - x - = + ]
= 34
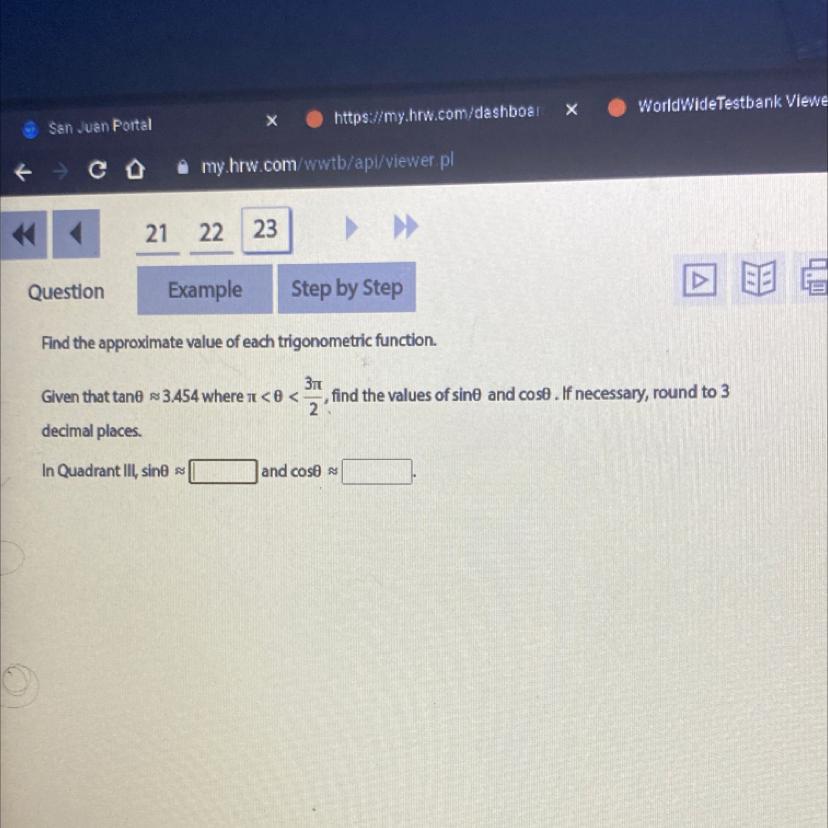
Find the approximate value of each trigonometric function.
31
Given that tano 3.454 where << find the values of sine and cose. If necessary, round to 3
2
decimal places.
In Quadrant III, sino s
and cost
Answers
Answer:
Given
tanθ = 3.454θ is in the III quadrantWe know in the III quadrant both sine and cosine are negative.
Use the following identities to get values of sinθ and cos θ
sinθ = - tanθ/√(1 +tan²θ) cosθ = - 1/√(1 +tan²θ)Substitute the value of tanθ and find sine and cosine:
sinθ = - 3.454/√(1 + 3.454²) = - 0.961cosθ = - 1/√(1 + 3.454²) = - 0.278Find the value of k>0 so that the plane 2x−2y+z=k is tangent to the sphere x2+y2+z2−96z=0.
Answers
The value of k>0 that makes the plane 2x−2y+z=k tangent to the sphere x2+y2+z2−96z=0 is k=96.
To find the value of k that makes the plane tangent to the sphere, we can compare the coefficients of x, y, and z in the equation of the plane and the equation of the sphere.
The equation of the plane is 2x−2y+z=k, where the coefficients of x, y, and z are 2, -2, and 1, respectively.
The equation of the sphere is x^2+y^2+z^2−96z=0, where the coefficient of z is -96.
Since the plane is tangent to the sphere, the coefficients of x, y, and z must be proportional to the coefficients of x, y, and z in the equation of the sphere.
Therefore, k=96, as the coefficient of z in the plane equation matches the coefficient of z in the sphere equation.
Learn more about Tangent click here :brainly.com/question/14022348
#SPJ1
find the reciprocal of 3
Answers
Find the volume of the solid.

Answers
The volume of the solid s solved to be 216 cubic m
How to find the volume of the composite solidVolume is calculated using the three dimensions, hence to talk about volume we have a 3 dimensional perspective.
The formula for volume is given as the product of length, width, and depth or thickness.
For the solid we divide into two and solve for the volumes separately then add together
Section 1
= 10 x 6 x 2
= 120 cubic m
Section 2
= 6 x 4 x (6 - 2)
= 96 cubic m
Volume of the solid
= 96 + 120
= 216 cubic m
Learn more about volume at
brainly.com/question/1972490
#SPJ1
A cookout tray consists of one main item, two different sides, and a drink. if cookout offers 10 main items, 10 sides, and 5 drinks, how many unique cookout trays are possible?
Answers
The number of unique cookout trays possible are 5,000.
Given data:
To calculate the number of unique cookout trays, consider the combinations of main items, sides, and drinks.
There are 10 options for the main item.
For the two sides, we have 10 options for the first side and 10 options for the second side.
For the drink, there are 5 options.
To find the total number of unique cookout trays, multiply the number of options for each category:
Total number of unique cookout trays = 10 (main items) * 10 (first side) * 10 (second side) * 5 (drinks)
= 5,000
Hence, there are 5,000 unique cookout trays possible with the given options for the main item, sides, and drinks.
To learn more about combinations, refer:
https://brainly.com/question/28065038
#SPJ4
can someone helpp with this

Answers

number that you add to -4 to give answer of 9
Answers
The number you need to add to -4 to get an answer of 9 is 13.
We can write this mathematically as:
-4 + x = 9
where x is the unknown number we need to find.
To solve for x, we can add 4 to both sides of the equation:
-4 + 4 + x = 9 + 4
Simplifying the left-hand side, we get:
x = 13
So the number we need to add to -4 to get 9 is 13.
The first step in combining the functions is to use a variable to represent one of the functions to make it easier to use. Rewrite x(y) so that the function it represents is equal to z.
Answers
The required composite function is fox = 24y² - 145.
Rewrite x(y) so that the function it represents is equal to z is z = 4y² - 25.
The function f(x) = 6x + 5 in terms of z is f(z) = 6z + 5.
What is a function?In Mathematics, a function can be defined as a mathematical expression which is typically used for defining and representing the relationship that exists between two or more variables such as an ordered pair.
Based on the information provided, we have the following functions;
f(x) = 6x + 5
x(y) = 4y² – 25
Next, we would create the required composite function as follows:
fox = 6[4y² - 25] + 5
fox = 24y² - 150 + 5
fox = 24y² - 145
By rewrite x(y) to represent z, we have:
z = 4y² - 25
In terms of z by substituting z for x, we have:
f(x) = 6x + 5
f(z) = 6z + 5
Read more on function here: brainly.com/question/3632175
#SPJ1
Complete Question:
The first step in combining the functions is to use a variable to represent one of the functions to make it easier to use. Rewrite x(y) so that the function it represents is equal to z.
a. In this activity, you'll combine two related functions, f(x) = 6x + 5 and x(y) = 4y² – 25, to create a type of function called a composite function. Then you’ll evaluate the composite function.
b. The first step in combining the functions is to use a variable to represent one of the functions to make it easier to use. Rewrite x(y) so that the function it represents is equal to z.
c. Write the function f(x) = 6x + 5 in terms of z by substituting z for x in the function.
Answer: ents is equal to z is z = 4y² - 25.
The function f(x) = 6x + 5 in terms of z is f(z) = 6z + 5.
What is a function?
In Mathematics, a function can be defined as a mathematical expression which is typically used for defining and representing the relationship that exists between two or more variables such as an ordered pair.
Based on the information provided, we have the following functions;
f(x) = 6x + 5
x(y) = 4y² – 25
Next, we would create the required composite function as follows:
fox = 6[4y² - 25] + 5
fox = 24y² - 150 + 5
fox = 24y² - 145
By rewrite x(y) to represent z, we have:
z = 4y² - 25
In terms of z by substituting z for x, we have:
f(x) = 6x + 5
f(z) = 6z + 5
Read more on function here: brainly.com/question/3632175
#SPJ1
Complete Question:
The first step in combining the functions is to use a variable to represent one of the functions to make it easier to use. Rewrite x(y) so that the function it represents is equal to z.
a. In this activity, you'll combine two related functions, f(x) = 6x + 5 and x(y) = 4y² – 25, to create a type of function called a composite function. Then you’ll evaluate the composite function.
b. The first step in combining the functions is to use a variable to represent one of the functions to make it easier to use. Rewrite x(y) so that the function it represents is equal to z.
c. Write the function f(x) = 6x + 5 in terms of z by substituting z for x in the function.
Step-by-step explanation:
when a coin is tossed three times, what is the probability that all three tosses are heads? the possible outcomes for the coin tosses are{hhh,ttt,htt,hht,thh,tth,hth,tht}
Answers
The probability of getting all three tosses to head is 1/8.
We have,
When a coin is tossed, there are two possible outcomes:
heads (H) or tails (T).
Since there are three tosses, the total number of possible outcomes.
2³ = 8.
The probability of getting heads on one toss is 1/2.
The probability of getting heads on all three tosses is the product of the probabilities of getting heads on each individual toss:
P(HHH) = P(H) x P(H) x P(H) = (1/2) x (1/2) x (1/2) = 1/8.
Therefore,
The probability of getting all three tosses to head is 1/8.
Learn more about probability here:
https://brainly.com/question/14099682
#SPJ1