Mark this question A poll conducted a week before the school election to the student council showed that Anjali would win with 58% of the vote. The margin of error was 7%. Choose the statement that correctly describes the confidence interval. O Anjali is predicted to win 58% or less of the vote. Anjali is predicted to win between 58% to 65% of the vote. O Anjali is predicted to win 58% or more of the vote. O Anjali is predicted to receive as much as 65% of the vote or as little as 51%
Answers
Anjali is predicted to win between 51% to 65% of the vote.
Since the margin of error is 7%, the 95% confidence interval is calculated as Anjali's predicted percentage plus/minus the margin of error.
So the interval is 58% +/- 7%, which gives a range of 51% to 65%. Therefore, the correct statement is "Anjali is predicted to receive as much as 65% of the vote or as little as 51%."
To know more about margin of error refer here
https://brainly.com/question/29101642#
#SPJ11
Related Questions
The equation y = 0.79x + 27 represents the amount a truck rental company charges, y, for each mile driven x. Interpret the slope and the y-intercept.
The slope represents a(n) (CHOOSE… does it increase or decrease?) of (CHOOSE… $0.79 or $27) for each mile driven.
The y-intercept represents the the truck rental company charges (CHOOSE… $0.79 or $27) for a truck rental when 0 miles are driven.
Answers
Answer:
Step-by-step explanation:
for equation y=0.79x+27
slope =0.79
y intercept =put x=0
=27
A box is formed by cutting squares from the four corners of a sheet of paper and folding up the sides. However, the size of the paper is unknown! The function f determines the volume of the box (in cubic inches) given a cutout length (in inches) a. Use function notation to represent the volume of the box (in cubic inches) when the cutout length is 0.8 inches Preview syntax error b. Use function notation to represent the volume of the box (in cubic inches) when the cutout length is 1.2 inches. Preview 20 c. Use function notation to represent how much the volume of the box (in cubic inches) changes by if the cutout length increases from 0.8 inches to 1.2 inches. /1.2)1.2-(10.8)0.8 Preview d. Use function notation to represent how much the volumne of the box (in cubic inches) changes by if the cutout length increases from 5.6 inches to 5.7 inches.
Answers
a) The volume of the box (in cubic inches) when the cutout length is 0.8 inches can be represented using function notation as f(0.8).
b) The volume of the box (in cubic inches) when the cutout length is 1.2 inches can be represented using function notation as f(1.2).
c) The change in volume of the box (in cubic inches) when the cutout length increases from 0.8 inches to 1.2 inches can be represented using function notation as f(1.2) - f(0.8).
d) The change in volume of the box (in cubic inches) when the cutout length increases from 5.6 inches to 5.7 inches can be represented using function notation as f(5.7) - f(5.6).
To know more about volume refer here
https://brainly.com/question/28058531#
#SPJ11
Use identities to write each equation in terms of the single angle θ. Then solve the equation for 0≤θ<2π. cos 2θ=-2 cos²θ
Answers
We can use the unit circle or reference angles. For the range O≤θ<2π, let's find the solutions: The solutions for θ in the given equation are θ = π/3, 2π/3, 4π/3, and 5π/3.
To write the equation in terms of a single angle, we can use the double-angle identity for cosine:
cos(2θ) = 2cos^2(θ) - 1
Given the equation cos(2θ) = -2cos^2(θ), we can substitute the right side of the equation with the double-angle identity:
2cos^2(θ) - 1 = -2cos^2(θ)
Now, let's simplify the equation:
2cos^2(θ) - 1 + 2cos^2(θ) = 0
Combining like terms:
4cos^2(θ) - 1 = 0
Now, let's isolate cos^2(θ) by moving -1 to the other side:
4cos^2(θ) = 1
Dividing both sides by 4:
cos^2(θ) = 1/4
Taking the square root of both sides:
cos(θ) = ±√(1/4)
cos(θ) = ±1/2
Now, we have two equations:
1) cos(θ) = 1/2
2) cos(θ) = -1/2
To solve for θ, we can use the unit circle or reference angles. For the range O≤θ<2π, let's find the solutions:
1) cos(θ) = 1/2:
θ = π/3 and θ = 5π/3
2) cos(θ) = -1/2:
θ = 2π/3 and θ = 4π/3
Therefore, the solutions for θ in the given equation are:
θ = π/3, 2π/3, 4π/3, and 5π/3.
To learn more about unit circle visit:
brainly.com/question/16897447
#SPJ11
A savings account increases from 150$ to 153$. What is the percent increase of the savings account?
Answers
Answer:
The correct answer would be 2.00%
Find the distance (7,9) and (1,1) using the phythagorean theorem
Plsss I really need the answer
Answers
Answer:
Using the Pythagorean theorem we can first put the points into x and y
x1 = 7
y1 = 9
x2 = 1
y2 = 1
The distance between the two points can be found as follows:
d = √((x2 - x1)² + (y2 - y1)²)
= √((1 - 7)² + (1 - 9)²)
= √((-6)² + (-8)²)
= √(36 + 64)
= √100
= 10
Therefore, the distance between the points (7, 9) and (1, 1) is 10 units.
The equation \(f(x)=7a^{2+x}-b\) has an x-intercept equivalent to
A) \(x=\frac{logb-log7}{loga}-2\)
B) \(x=7a^{2}-b\)
C) \(x=\frac{y+b}{7a^{2}}\)
D) \(x=0\)
I have the answer key so I know the answer. I just don't know how they got to the answer so please show your work.
Answers
Answer:
\(\textsf{A)} \quad x=\dfrac{\log b - \log 7}{ \log a}-2\)
Step-by-step explanation:
Given function:
\(f(x)=7a^{2+x}-b\)
The x-intercepts occur when the function equals zero.
\(\implies 7a^{2+x}-b=0\)
Add b to both sides:
\(\implies 7a^{2+x}=b\)
Divide both sides by 7:
\(\implies a^{2+x}=\dfrac{b}{7}\)
Take logs of both sides of the equation:
\(\implies \log \left(a^{2+x}\right)= \log \left(\dfrac{b}{7}\right)\)
\(\textsf{Apply the Power log law}: \quad \log_ax^n=n\log_ax\)
\(\implies (2+x)\log a= \log \left(\dfrac{b}{7}\right)\)
\(\textsf{Apply the Quotient log law}: \quad \log_a\frac{x}{y}=\log_ax - \log_ay\)
\(\implies (2+x)\log a= \log b-\log 7\)
Divide both sides by log a:
\(\implies 2+x=\dfrac{\log b - \log 7}{ \log a}\)
Subtract 2 from both sides:
\(\implies x=\dfrac{\log b - \log 7}{ \log a}-2\)
Need help!!! Please!!

Answers
Answer:
\(\huge\boxed{\text{(A)}\ 0.36}\)
Step-by-step explanation:
This sequence will have a pattern. Our goal is to try and find this pattern.
Our first two numbers are -45 and 9. The first relationship between these numbers that pops into my mind is 5. \(9 \cdot 5 = 45\). However, we go from -45 to 9. This means we have to divide by -5. \(-45 \div -5 = 9\)
Let's check this actually is what the sequence is. It would be true if \(9 \div -5 = -1.8\).
\(9 \div -5 = -1.8\)
So -5 is the divisor.
To find the next term in the sequence, we divide -1.8 by -5.
\(-1.8 \div -5 = 0.36\)
Hope this helped!
Factor the polynomial
3x^4 – 2x^2 + 15x^2 –10 by grouping.
Which product is the factored form of the polynomial?
A.
\(( - x {}^{2} - 5)(3x {}^{2} + 2)\)
B.
\((x {}^{2} - 2)(3x {}^{2} + 5)\)
C.
\((x {}^{2} + 5)(3x {}^{2} - 2)\)
D.
\((3x {}^{2} - 5)(x {}^{2} + 2)\)
Answers
The product that is the factored form of the polynomial 3x⁴ - 2x² + 15x² - 10 is (x² + 5)(3x² - 2).
What is a polynomial?In mathematics, a polynomial is an expression consisting of indeterminates (also called variables) and coefficients, that involves only the operations of addition, subtraction, multiplication, and positive-integer powers of variables.
The polynomial is first correctly stated as follows
\(\sf 3x^4 - 2x^2 + 15x^2 -10\)This is rearranged, grouped and solved as follows:
\(\sf 3x^4+15x^2-2x^2-10\)
\(\sf (3x^4+15x^2)-(2x^2+10)\)
\(\sf 3x^2(x^2+5)-2(x^2+5)\)
Factorizing the common factors, we have the product of the factored form of the polynomial as follows:
\(\boxed{\rightarrow\bold{(x^2 + 5)(3x^2 - 2)}}\)
Thus, the product that is the factored form of the polynomial 3x⁴ - 2x² + 15x² - 10 is (x² + 5)(3x² - 2).
Learn more about the polynomial at:
https://brainly.com/question/30520457
Luis uses 1.6 liters of gasoline each hour he spends mowing lawns. How much gas does he use in 5.8 hours?
can someone please help me? I'm really not a fan of the subject math, and I'm currently struggling and my math grade isn't good at the moment AND grade book closes next week friday :(
Answers
Answer:
9.28 liters
Step-by-step explanation:
The unit rate is 1.6 liters per hour.
You multiply it by the number of hours
1.6 x 5.8 = 9.28
Answer:
9.28.
Step-by-step explanation:
We're trying to find out how much gas Luis uses in 5.8 hours. It states that Luis uses 1.6 liters of gasoline EACH HOUR. So, we just multiply 1.6 and 5.8.
Is (7,0) (7,-5) (7,-8) (7,4) (7,3) a function
Answers
The ordered pair (7,0) (7,-5) (7,-8) (7,4) (7,3) is not a function
How to determine if it is a functionFrom the question, we have the following parameters that can be used in our computation:
(7,0) (7,-5) (7,-8) (7,4) (7,3)
A function is a set of ordered pairs, where for each input (x-value) there is exactly one output (y-value).
In the given set of ordered pairs, the x-value 7 is repeated multiple times and has different y-values, which violates the definition of a function.
Read more about functions a
https://brainly.com/question/22340031
#SPJ1
if x 2/3 = 9 find x
pls help
Answers
find the value of 3x-2 when x=4
find the value of 5x+6 when x=-2
Answers
Answer:
3(4) - 2 is 10 the value is 10
5(2) + 6 is 16 the value is 16
I hope this helps have a good day or night!
Two fifteenths times 10
Answers
Answer:
1.3
Step-by-step explanation:
if p1, p2,… , pn are n propositions, explain why ⋀n−1 i=1 ⋀n j=i 1 (¬pi ∨ ¬pj ) is true if and only if at most one of p1, p2,… , pn is true.
Answers
we have shown that ⋀n−1 i=1 ⋀n j=i 1 (¬pi ∨ ¬pj) is true if and only if at most one of p1, p2,..., pn is true.
What is the Boolean algebra?
Boolean algebra is a branch of mathematics that deals with operations on logical values and variables, named after the mathematician George Boole.
Hence, we have shown that ⋀n−1 i=1 ⋀n j=i 1 (¬pi ∨ ¬pj) is true if and only if at most one of p1, p2,..., pn is true.
Let's break down the expression ⋀n−1 i=1 ⋀n j=i 1 (¬pi ∨ ¬pj) into its component parts:
⋀n−1 i=1: This means we are taking the conjunction (logical AND) of the following expression for all values of i from 1 to n-1.⋀n j=i 1: This means we are taking the conjunction of the following expression for all values of j from i to n.(¬pi ∨ ¬pj): This is the expression being conjoined in steps 1 and 2. It is a disjunction (logical OR) of the negation of propositions pi and pj.Now, let's consider what happens when we evaluate this expression:
If at least two of the propositions p1, p2, ..., pn are true, then for some i and j (where i ≠ j), both pi and pj are true. In this case, ¬pi ∨ ¬pj is false, since both pi and pj are true, and the conjunction of any number of false statements is always false. Therefore, the entire expression ⋀n−1 i=1 ⋀n j=i 1 (¬pi ∨ ¬pj) must be false if at least two of the propositions are true.To learn more about Boolean algebra, Visit
https://brainly.com/question/2467366
#SPJ1
Please help! I will give brainliest.

Answers
Answer:
Therefore, the measure of ∠x is 33 degrees.
Step-by-step explanation:
As angle ∠S is a right angle and angles ∠R and ∠x are complementary, we have:
∠R + ∠x = 90 degrees
Substituting the given values, we get:
57 + ∠x = 90
∠x = 90 - 57
∠x = 33 degrees
Answer: x = 32°
Step-by-step explanation: triangle of ABC = 58°, 90° & x°
x = 180°-148° = 32°
(x° is equal to the unknown° where C is, as well as 58° where A is)
Is 89/10 rational or irrational
Answers
Answer:
Yes
Step-by-step explanation:
For 89 to be a rational number, the quotient of two integers must equal 89. In other words, for 89 to be a rational number, 89 must be able to be expressed as a ratio where both the numerator and the denominator are integers (whole numbers). ... Thus, the answer to the question "Is 89 a rational number?" is YES.
on her way to visit her parents, jennifer drives 265 miles in 5 hours what is her average rate of speed in miles per hour?
Answers
Answer:
53 miles per hour
Step-by-step explanation:
To calculate Jennifer's average rate of speed in miles per hour, we can use the formula:
average speed = total distance / total time
In this case, Jennifer drove a total distance of 265 miles and it took her a total time of 5 hours, so:
average speed = 265 miles / 5 hours
Simplifying the expression, we get:
average speed = 53 miles per hour
Therefore, Jennifer's average rate of speed in miles per hour is 53 miles per hour.
Answer: 53 miles per hour
Step-by-step explanation:
To find Jennifer's average rate of speed in miles per hour, we divide the distance she traveled by the time it took her:
Average speed = distance ÷ time
Average speed = 265 miles ÷ 5 hours
Average speed = 53 miles per hour
Therefore, Jennifer's average rate of speed was 53 miles per hour.
please help with these 2 questions in math!! thank uu!!

Answers
Answer:
sorry if wrong again but for a put (r+y) (a+b)
for b put (pq-\(r^{2}\)) x (9-1)
Step-by-step explanation:
need quick help on this math problem
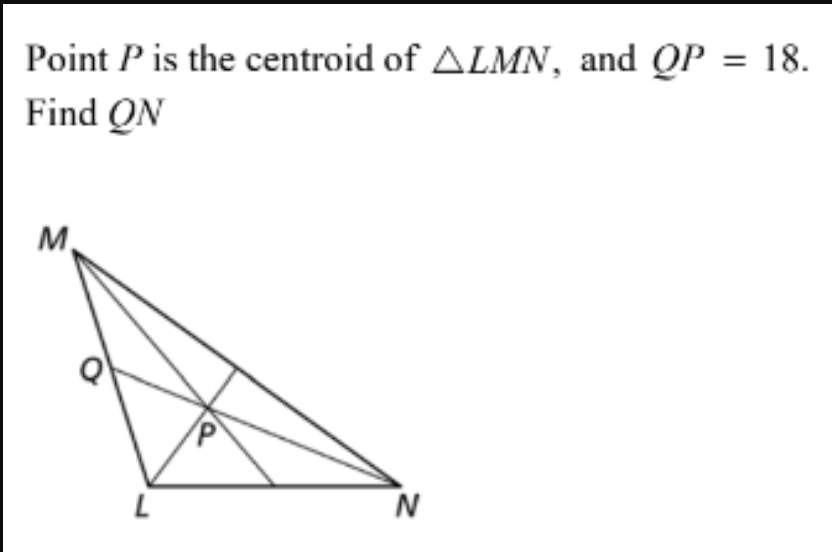
Answers
The length QN on the triangle is 54 units
How to determine the length QNFrom the question, we have the following parameters that can be used in our computation:
Point P = Centroid
Also, we have
QP = 18
The centroid divides each median into the ratio 2:1.
Using the above as a guide, we have the following:
QN = 3 * QP
Substitute the known values in the above equation, so, we have the following representation
QN = 3 * 18
Evaluate
QN = 54
Hence, the length is 54 units
Read more about centroid at
https://brainly.com/question/7644338
#SPJ1
How do you simplify this question

Answers
Answer:
38/5m
Step-by-step explanation:
Solution
= 2/5m - 4/5- 3/5
take 5 common in denominators
= 2-4+3/5
38/5m
The time t required to empty a tank varies inversely as
the rate r of pumping. If a pump can empty a tank in
45 minutes at a rate of 300 gallons per minute, how
long will it take to empty a tank at 500 gallons per
minute?
k
Answers
If \(t\) and \(r\) are inverse proportional to one another, then for some constant volume \(V\) we have
\(V = tr\)
It takes 45 min to empty a tank containing at 300 gal/min, so the tank contains
\(V = (45\,\mathrm{min}) \left(300\dfrac{\rm gal}{\rm min}\right) = 13500\,\mathrm{gal}\)
of liquid.
If it's emptied at 500 gal/min, it would take
\(13500\,\mathrm{gal} = t \left(500\dfrac{\rm gal}{\rm min}\right) \implies t = \boxed{27\,\mathrm{min}}\)
FIND THE SLOPE BETWEEN THE FOLLOWING POINTS!!!
15 POINTS
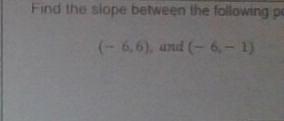
Answers
The slope between the points (-6, 6) and (-6, -1) is -infinity.
How to find the slope of a line?The slope of a line is the change in the dependent variable with respect with the change in the independent variable.
Therefore, the slope is define as rise over run.
Hence let's find the slope between the points (-6, 6) and (-6, -1)
Therefore,
slope = y₂ - y₁ / x₂ - x₁
x₁ = -6
x₂ = -6
y₁ = 6
y₂ = -1
Therefore,
slope = -1 - 6 / -6 + 6
slope = -7 / 0
slope = - infinity
learn more on slope here:https://brainly.com/question/15166299
#SPJ1
3 less than or equal to p/12
Answers
Answer:
p greater than or equal to 36
please help me with this


Answers

who developed the first satellite
Answers
Answer:
Russia
Step-by-step explanation:
Russia made the Sputnik satelite
Answer:
Soviet Union has developed world's first satellite

Can someone help me on this

Answers
Answer:
Step-by-step explanation:
14y-1=11y+17 subtract 11y from both sides
3y-1=17 add 1 to both sides
3y=18, divide both sides by 3
y=6
Since DG=EF
EF=9y+4 and using y=6
EF=9(6)+4
EF=54+4
EF=58
The following is a composite figure. Find the TOTAL AREA of
the figure.
16 in
8 in
16 in
8 in
inches
Answers
for area , you multiply length times height so it’d be 16 x 8 :)
Using the formula below, determine the monthly payment on a 5 year car loan with a monthly percentage rate of 0.625% for a car with an original cost of $21,000 and a $1,000 down payment, to the nearest cent.
Pn = PMT ((1-(1+i)-n)/i)
Pn= present amount borrowed
n= number of monthly pay periods
PMT= monthly payment
i= interest rate per month
Answers
To determine the monthly payment on a 5-year car loan with a monthly percentage rate of 0.625%, we need to calculate the present amount borrowed (Pn) and then use the given formula to solve for the monthly payment (PMT).
Given:
Original cost of the car (Pn) = $21,000
Down payment = $1,000
Monthly interest rate (i) = 0.625% = 0.00625
Number of monthly pay periods (n) = 5 years * 12 months/year = 60 months
First, calculate the present amount borrowed (Pn):
Pn = Original cost - Down payment
Pn = $21,000 - $1,000
Pn = $20,000
Now, use the formula to calculate the monthly payment (PMT):
PMT = Pn * ((1 - (1 + i)^(-n)) / i)
PMT = $20,000 * ((1 - (1 + 0.00625)^(-60)) / 0.00625)
Calculating this expression using a calculator or spreadsheet, the monthly payment (PMT) is approximately $377.42 (rounded to the nearest cent).
Therefore, the monthly payment on the 5-year car loan is approximately $377.42.
Learn more about percentage here: brainly.com/question/32388485
#SPJ11
here are seven boys and six girls in a class. the teacher randomly selects one student to answer a question. later, the teacher randomly selects a different student to answer another question. find the probability that the first student is a boy and the second student is a girl.
Answers
The probability that the first student is a boy and the second student is a girl is 7/26.
To answer your question, we'll need to calculate the probabilities for each event and then multiply them together.
Probability of selecting a boy first:
There are 7 boys and 13 students total (7 boys + 6 girls), so the probability is 7/13.
Probability of selecting a girl second:
After selecting a boy, there are now 12 students remaining (6 boys + 6 girls). The probability of selecting a girl is 6/12 (which simplifies to 1/2).
Now, multiply the probabilities together: (7/13) × (1/2) = 7/26
So, the probability that the first student is a boy and the second student is a girl is 7/26.
To learn more about probability here:
brainly.com/question/30034780#
#SPJ11
Suppose you know that ∠S and ∠Y are complementary, and that m∠S = 5(m∠Y) − 210°. Find m∠Y.
Answers
Answer:
m∠Y = 50°
Step-by-step explanation:
let 'm' = m∠Y
m∠S + m∠Y = 90 (complementary)
5m - 210 + m = 90
6m = 300
m = 50