Margin of error: 0.04; confidence level: 95%; from a prior study, p is estimated by the decimal equivalent of 60%
A) 577 B) 1441 C) 996 D) 519
Answers
The required sample size of the given value is 577.
What is margin of error?
In a random survey sample, a margin of error is a statistical measurement that takes into account the discrepancy between actual and anticipated findings. Simply said, you may determine the degree of unpredictability in data and research results using the margin of error.The formula to calculate the sample size :-
n = (p(1-p)((Zα/₂)/E)²
Given : Estimated proportion p = 0.60
Margin of error : E = 0.04
Significance level : α = 1-0.95 = 0.05
Critical value : Zα/₂ = 1.96
Now, the required sample size will be :-
n = (0.60)(0.11)(1.96/0.04)²
= 6.6 * (0.0784)²
= 0.57744
Hence, the required minimum sample size of the given is 577.
To know more about margin of error check the below link:
https://brainly.com/question/24289590
#SPJ1
Related Questions
What is the value of the digit in the ones place?
2,615
A. 50
B. 5
OC. 2,000
OD. 100
Answers
The United States earned 104 medals at the 2012 summer olympics. The number of silver medals earned was the same as the number of bronze medals. The number of gold medals was 17 more than the number of silver medals. How many of each kind of medal did the united states earn?
Answers
Answer-29 bronze, 46 gold,and 29 silver.
The first thing to do is take 104 and subtract the 17 medal difference between them all. This is 87. Next we divided 87 into three, which gives us 29. Now we have 29 medals for silver, bronze, and gold. However we must add 17 to the gold medals that we took away earlier. 29+17 is 46. To make sure this is correct we can add 29+29+46. This equals 104, which our original answer, so this was correct.
In 2012 the United States earned 29 bronze medals, 46 gold medals, and 29 silver medals.
HOPE THIS HELPS!! GOOD LUCK!!! <3
Find the volume of a cone with a base radius of 3in and a height of 11in. Use the value 3.14 for π, and do not do anu rounding. Be Sure to include the correct unit in your answer.
Answers
So the formula to find the volume of a cone is,
\(V = \pi r^{2} \frac{h}{3}\)
Given,
Base of the cone is 3 inchesHeight of the cone is given as 11 inchesTo Find : The Volume of the cone
Applying the values we get,
\(V = 3.14X(3)^{2} X \frac{11}{3}\)
\(V = 28.26X\frac{11}{3}\)
\(V = 103.62in^{3}\)
Hence , the volume of the cone is 103.62in³
You are given the expressions x(3.25y - 4.86) and x(-1.75y + 5y - 3.86) + x. A. Expand each expression. B. Are these expressions equivalent? Explan?
Answers
Expansion of x(3.25y - 4.86) is 3.25xy - 4.86x and expansion of
x(-1.75y + 5y - 3.86) + x is 3.25xy - 2.86x. The expressions are not equivalent as the coefficient of x is different in the expanded form.
What are equivalent expressions?
In expanded form, the expression combines all its like terms.
Two expressions are equivalent if they can be simplified to the same third expression or if one of the expressions can be written like the other.
According to the given question:
The given expressions are
1. x (3.25y - 4.86)
2. x (-1.75y + 5y - 3.86) + x
Expanding each expression
1. x (3.25y - 4.86)
= 3.25*x*y - 4.86*x
= 3.25xy - 4.86x
2. x (-1.75y + 5y - 3.86) + x
= -1.75*x*y + 5*x*y - 3.86*x + x
= 3.25xy - 2.86x
Clearly coefficient of x variable is different after expansion of expressions. Therefore, the expressions are not equivalent.
To know more about equivalent expressions visit
https://brainly.com/question/28170201
#SPJ1
Working on summer vacation. Suppose in a school it is found that 30% of adults do not work at all while on sum- mer vacation. In a random sample of 8 adults, let x repre sent the number who do not work during summer vacation.
a. For this experiment, define the event that represents a "success
b. Explain why x is (approximately) a binomial random variable.
c. Give the value of p for this binomial experiment.
d. Find P(x-3) e. Find the probability that 2 or fewer of the 8 adults do not work during summer vacation.
Answers
Answer:
(a) The event that represents success here is the percentage of adults who do not work at all while on summer vacation.
(b) X is a binomial random variable.
(c) The value of p for this binomial experiment is 0.30 or 30%.
(d) P(X = 3) = 0.2541.
(e) The probability that 2 or fewer of the 8 adults do not work during summer vacation is 0.5518.
Step-by-step explanation:
We are given that in a school it is found that 30% of adults do not work at all while on summer vacation. In a random sample of 8 adults, let X represent the number who do not work during summer vacation.
Let X = the number of adults who do not work during summer vacation
(a) The event that represents success here is the percentage of adults who do not work at all while on summer vacation.
(b) The conditions required for any variable to be considered as a random variable is given by;
The experiment consists of identical trials.Each trial must have only two possibilities: success or failure.The trials must be independent of each other.So, in our question; all these conditions are satisfied which means X is a binomial random variable.
(c) The value of p for this binomial experiment is 0.30 or 30%.
(d) The above situation can be represented through binomial distribution;
\(P(X = r) = \binom{n}{r}\times p^{r} \times (1-p)^{n-r}; x = 0,1,2,......\)
where, n = number of trials (samples) taken = 8 adults
r = number of success = exactly three
p = probability of success which in our question is % of adults who
do not work at all while on summer vacation, i.e; p = 0.25
SO, X ~ Binom(n = 8, p = 0.30)
Now, the probability that exactly 3 adults do not work at all while on summer vacation is given by = P(X = 3)
P(X = 3) = \(\binom{8}{3}\times 0.30^{3} \times (1-0.30)^{8-3}\)
= \(56 \times 0.30^{3} \times 0.70^{5}\)
= 0.2541
(e) The probability that 2 or fewer of the 8 adults do not work during summer vacation is given by = P(X \(\leq\) 2)
P(X \(\leq\) 2) = P(X = 0) + P(X = 1) + P(X = 2)
= \(\binom{8}{0}\times 0.30^{0} \times (1-0.30)^{8-0}+\binom{8}{1}\times 0.30^{1} \times (1-0.30)^{8-1}+\binom{8}{2}\times 0.30^{2} \times (1-0.30)^{8-2}\)
= \(1 \times 0.30^{0} \times 0.70^{8}+8 \times 0.30^{1} \times 0.70^{7}+28\times 0.30^{2} \times 0.70^{6}\)
= 0.5518
What is the outlier for the data set?
19, 19, 27, 21, 77, 18, 23, 29
Answers
Answer: 77
Step-by-step explanation:
will give BRAINLIEST ANSWER THE IMAGE

Answers
Answer:
Line n bisects segment XY
The length of segment XY = 6
Step-by-step explanation:
Line n is the segment bisector of segment XY
A bisector is to divide into two equal parts, so;
5x + 8 = 9x + 12
4x = -4
x = -1
Total segment = 5x + 8 + 9x + 12
plug in -1 for x;
-5 + 8 + -9 + 12
XY = 3 + 3
XY = 6
Answer:
the answer i came up with for the first question the answer is C
for the second question, i go 11.4
Step-by-step explanation:
how i got 11.4 add all like valuables
12+8=20
9x+5x=14x
then divide to get x alone to get 11.4
What does the notation P(B|A) mean? Question content area bottom Part 1 Choose the correct answer below. A. The probability of event B occurring, given that event A has occurred B. The probability of event B occurring, divided by the probability of event A occurring C. The probability of event A occurring, given that event B has occurred D. The probability of both event A and event B occurring
Answers
Answer:
A. The probability of event B occurring, given that event A has occurred
Step-by-step explanation:
Conditional probability
A probability is conditional if is depends on what has already happened.
The probability that event B happens, given that event A has already happened is "B given A" or P(B | A)
Therefore, P(B | A) means "The probability of event B occurring, given that event A has occurred"
Additional information:
P(A | B) means "A given B", i.e. the probability of event A occurring, given that event B has occurred
P(A ∩ B) means the probability of event A and event B both happening.
HELP!! Which figure is a translation of Figure 1? *

Answers
Answer:
Figure B
Step-by-step explanation:
A translation moves a certain amount of spaces, but will never turn nor will it rotate.
Please answer correctly, I’ll give brainlest.

Answers
Answer:
\( \sqrt{170} \)
(-x^2+9xy)-(x^2+6xy-8y^2)
Answers
Answer: The result would be - 2x^2 + 3xy + 8y^2.
Step-by-step explanation:
(-x^2 + 9xy) - (x^2 + 6xy - 8y^2)
The objective of this question is to remove the brackets.
The first pair of brackets could simply be removed since it won't need changing (because it's positive, without symbols in front). As for the second one, we must remove the brackets in some way, which is to make basically every term in that bracket the negative of the 'original' ones.
The negative of x^2 = - x^2
The negative of + 6xy = - 6xy
The negative of - 8y^2 = + 8y^2
Combine them with the first two terms and it'll be like below.
= - x^2 + 9xy - x^2 - 6xy + 8y^2
Then, rearrange and sum all like terms together.
There are 2 sets of like terms:
First set: (- x^2 and- x^2)
Second set: ( + 9xy and - 6xy)
So, it becomes...
= - x^2 - x^2 + 9xy - 6xy + 8y^2
= - 2x^2 + 3xy + 8y^2
Jeremy read 243 pages on Saturday. He read 53 fewer pages on Sunday.
How many pages did he read in all?
Answers
243 = the pages read on Saturday
243 - 53 = 190 = the pages read on Sunday
190 + 243 = 433 = total pages read
Answer = 433
You can do like
(243+243-53)
As he read 53 less pages than on Saturday
I hope you got it : )
Tiffany sells musical instruments and equipment at Let It Rock in the mall. She earns a commission of 5% on the first $6,000, 7.5% on the next $6,000, and 10% on sales over $12,000. Her total sales for the month are $14,640. What is Tiffany’s total commission?
Answers
Answer:
$800
Step-by-step explanation:
5% × 6000 = $350
14640 - 6000 = $8640
7.5% × 6000 = $450
8640 - 6000 = $2640
350 + 450 = $800
Use Right Triangle Trigonometry to find the length of the hypotenuse. Round to the nearest whole number,

Answers
Answer:
13
Step-by-step explanation:
Use sin = opposite/hypotenuse
Setup an equation. I'm going to use x to represent the hypotenuse.
\(sin44=\frac{9}{x}\)
Now move the x to the other side by multiplying. We want to solve for x.
\(x(sin44)=(\frac{9}{x})x\)
The x cancels on the right side. Now divide both sides by sin44. To get by itself on the left.
\(\frac{x(sin44)}{sin44} = \frac{9}{sin44}\)
\(x = \frac{9}{sin44}\)
Use your scientific calculator, make sure it is on degrees, and divide 9 by sin44.
\(x = 12.9560088566\)
Round to the nearest whole number
\(x = 13\)
Show that the angle bisector of an equilateral triangle is perpendicular to the base
Answers
To show that the angle bisector of an equilateral triangle is perpendicular to the base, we can assume an equilateral triangle with sides ABC. Next, we can get an angle bisector in the middle represented by BD which becomes perpendicular to the base BC.
How to prove that the angle bisector is perpendicular to baseAfter getting the angle bisector, we would see that the line segment BD, divides angle BAC into two equal angles, each measuring 30 degrees. Now, we can draw a perpendicular line from point D to the base BC.
We could also draw a line E, which is the perpendicular line that intersects the base BC. We want to show that BD is perpendicular to BC, which means we need to show that angle BDE is a right angle.
Since the sum of angles BDA and ADE is 90 degrees (they form a right angle), and the sum of angles BAD, ABD, and BDA is 180 degrees, it follows that angle BDE must be a right angle.
Therefore, we have shown that the angle bisector of an equilateral triangle is perpendicular to the base.
Learn more about the angle bisector of an equilateral triangle here:
https://brainly.com/question/30341397
#SPJ1
Right triangle XYZ, with vertex _Y at (-3,0), is rotated clockwise 180° about the origin. Which of the following rotations is
equivalent to 180° clockwise rotation about the origin?
counterclockwise 180°
clockwise 270
counterclockwise 360°
clockwise 360°
Answers
what is the remainder when 849,400 is divided by 216
Answers
Answer:
The remainder is 88
Step-by-step explanation:
The Remainder of a Division
We have to find the remainder when we divide 849,400 by 216.
It could be found by doing the long division, but we'll do it with a calculator.
Entering the division in the calculator we get:
849,400/216=3,932.4074...
We take the whole part of the quotient (3,932) and multiply it by the divisor:
3,932*216=849,312
The remainder is obtained by subtracting 849,400-849,312=88
The remainder is 88
100 more than 365 is equal to 65more then
Answers
Answer:
x = 400Step-by-step explanation:
100 more than 365 is equal to 65more then
we can solve with an equation
100 + 365 = 65 + x
100 + 365 - 65 = x
465 - 65 = x
400 = x
------------
check
100 + 365 = 65 + 400
465 = 465
the answer is good
Which one of the following statements is correct when the homoskedasticity assumption is violated while the rest of the OLS assumptions are correct.?
a.The beta parameter estimates can be calculated but they are wrong.
b.The beta parameter estimates are biased
c.The beta parameter estimates are unbiased because homoskedasticity assumption is not required for unbiasedness.
d.The beta parameter estimates cannot be calculated
Answers
The correct answer is option b. When the homoskedasticity assumption is violated, The beta parameter estimates are biased while the rest of the OLS assumptions are correct.
When the homoskedasticity assumption is violated, the ordinary least squares (OLS) estimator is still consistent but no longer efficient. This means that the estimates of the regression coefficients (beta parameters) are still unbiased, but they have higher variances and covariances.
In other words, the OLS estimator is no longer the best linear unbiased estimator (BLUE) and it may be biased when the errors are heteroscedastic. Therefore, option b is correct.
Learn more about homoskedasticity assumption:
https://brainly.com/question/14745756
#SPJ4
Find the missing side

Answers
By using trigonometry, the missing sides are
Example 1: x = 16.7
Example 2: x = 3.2
Example 3: x = 23.5
Example 4: x = 9.3
Trigonometry: Determining the values of the missing sidesFrom the question we are to determine the value of the missing sides in the given triangles
We can determine the value of the missing sides by using SOH CAH TOA
Example 1
Angle = 42°
Opposite side = x
Hypotenuse = 25
Thus,
sin (42°) = x / 25
x = 25 × sin (42°)
x = 16.7
Example 2
Angle = 75°
Opposite side = 12
Adjacent side = x
Thus,
tan (75°) = 12 / x
x = 12 / tan (75°)
x = 3.2
Example 3
Angle = 36°
Hypotenuse side = x
Adjacent side = 19
Thus,
cos (36°) = 19 / x
x = 19 / cos (36°)
x = 23.5
Example 4
Angle = 53°
Opposite side = x
Adjacent side = 7
Thus,
tan (53°) = x / 7
x = 7 × tan (53°)
x = 9.3
Hence,
The missing sides are 16.7, 3.2, 23.5 and 9.3
Learn more on Trigonometry here: https://brainly.com/question/29195940
#SPJ1
A square pyramid has a base edge of 1 meter. The height of each triangular face is 1 meter. What is the pyramid's surface area?
Answers
Answer:
A square pyramid has 5 faces: 1 square base and 4 triangular faces.
The area of the base is:
A = s^2
where s is the length of the base edge.
In this case, s = 1 m, so:
A = 1^2 = 1 m^2
The area of each triangular face is:
A = 1/2 * b * h
where b is the base of the triangle (which is equal to the length of one side of the square base) and h is the height of the triangle (which is given as 1 m).
In this case, b = 1 m and h = 1 m, so:
A = 1/2 * 1 * 1 = 0.5 m^2
The total surface area of the pyramid is the sum of the area of the base and the area of the four triangular faces:
SA = A_base + 4 * A_triangles
SA = 1 + 4(0.5)
SA = 1 + 2
SA = 3 m^2
Therefore, the surface area of the pyramid is 3 square meters.
Use the information given below to find tan(a + B)
cos a = 3/5, with a in quadrant IV
tan B = 4/3, with B in quadrant I I I
Give the exact answer, not a decimal approximation.
tan(a + B) = ?
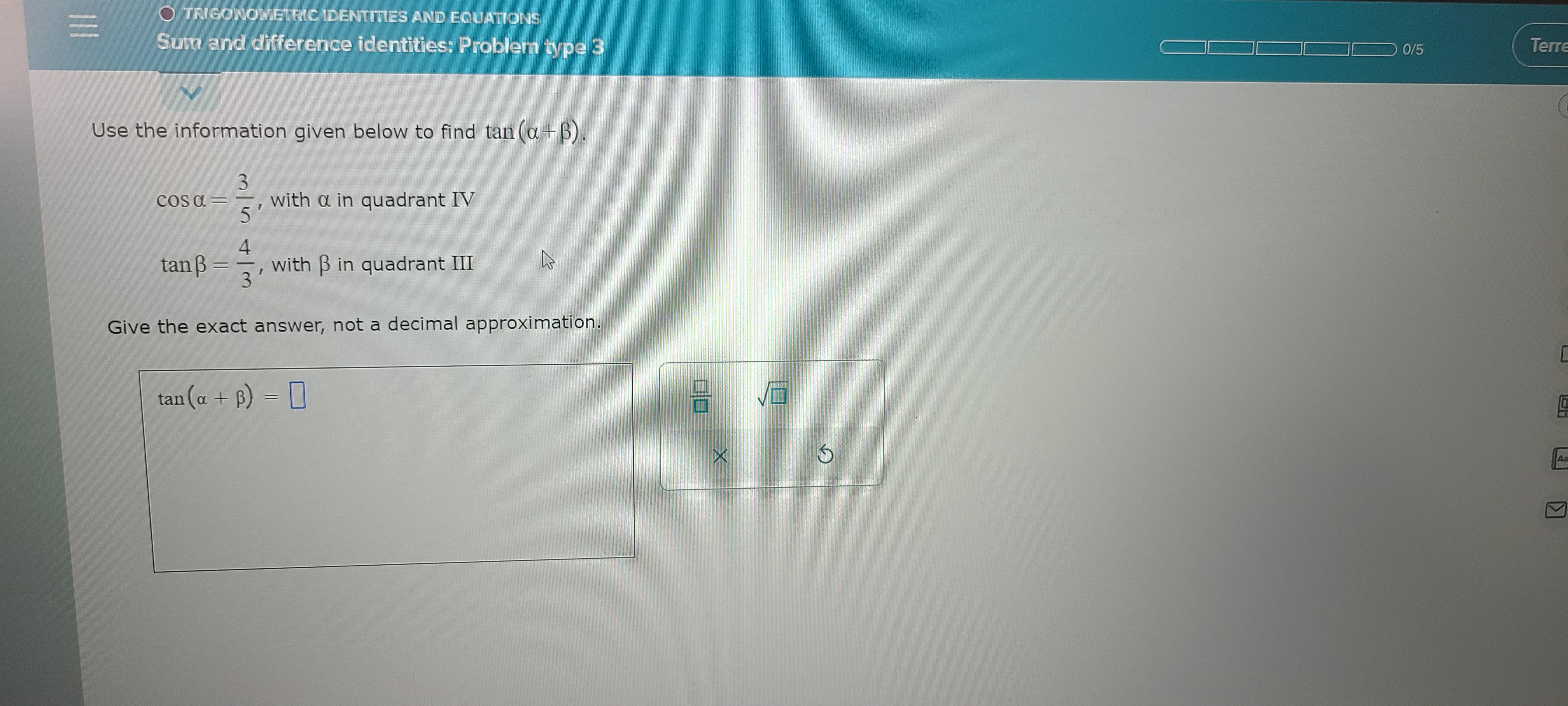
Answers
let's bear in mind that on the III Quadrant, sine and cosine are both negative, whilst on the IV Quadrant, sine is negative and cosine is positive, that said
\(\cos(\alpha )=\cfrac{\stackrel{adjacent}{3}}{\underset{hypotenuse}{5}}\hspace{5em}\textit{let's find the \underline{opposite side}} \\\\\\ \begin{array}{llll} \textit{using the pythagorean theorem} \\\\ a^2+o^2=c^2\implies o=\sqrt{c^2 - a^2} \end{array} \qquad \begin{cases} c=\stackrel{hypotenuse}{5}\\ a=\stackrel{adjacent}{3}\\ o=opposite \end{cases} \\\\\\ o=\pm \sqrt{ 5^2 - 3^2} \implies o=\pm \sqrt{ 16 }\implies o=\pm 4\implies \stackrel{IV~Quadrant }{o=-4} \\\\[-0.35em] ~\dotfill\)
\(\tan(\beta )=\cfrac{\stackrel{opposite}{4}}{\underset{adjacent}{3}}\implies \tan(\beta )=\cfrac{\stackrel{opposite}{-4}}{\underset{adjacent}{-3}} \\\\[-0.35em] ~\dotfill\\\\ \tan(\alpha + \beta) = \cfrac{\tan(\alpha)+ \tan(\beta)}{1- \tan(\alpha)\tan(\beta)} \\\\\\ \tan(\alpha + \beta)\implies \cfrac{ ~~\frac{-4}{3}~~ + ~~\frac{-4}{-3} ~~ }{1-\left( \frac{-4}{3} \right)\left( \frac{-4}{-3} \right)}\implies \cfrac{0}{1-\left( \frac{-4}{3} \right)\left( \frac{-4}{-3} \right)}\implies \text{\LARGE 0}\)
−0.22+�−0.33−0.22x+x−0.33x?
Answers
The answer to the equation −0.22x + x − 0.33x is 0.11x.
The answer is 0.11x. To solve this, we can start by rearranging the terms of the equation. The equation can be written as:
−0.22x + x − 0.33x = −0.22 + 0.33x
We then subtract x from both sides of the equation, resulting in:
−0.22x − x = −0.22 + 0.33x − x
We then combine like terms on the left side of the equation, resulting in:
−1.22x = −0.55
Finally, we divide both sides of the equation by -1.22 to solve for x, resulting in:
x = 0.11
Therefore, the answer is 0.11x.
Learn more about equation here:
https://brainly.com/question/10413253
#SPJ1
Complete question
What is the value of -0.22+−0.33−0.22x+x−0.33x?
Explain the difference between an indefinite integral and a definite integral.
A) An indefinite integral, after evaluating it at the limits of integration, results in a particular number. A definite integral results in a set of functions that share the same derivative and uses an arbitrary constant of integration.
B) A definite integral, after evaluating it at the limits of integration, results in a particular number. An indefinite integral results in a set of functions that share the same derivative and uses an arbitrary constant of integration.
C) An indefinte integral cannot always be integrated analytically and may require numeric integration, while it is always possible to integrate a definite integral. Definite integrals always return a real number after evaluation at its limits of integration.
D) A definite integral is defined and continuous over the interval of integration and has finite limits of integration. An indefinite integral is also defined and continuous over the interval of integration, but may have as a limit of integration.
Answers
The answer is A.
An indefinite integral is a function that, when differentiated, equals the original function. It is denoted by ∫f(x)dx, where f(x) is the function to be integrated. An indefinite integral always has an arbitrary constant of integration, which is denoted by C. This is because the derivative of any constant is zero, so the derivative of ∫f(x)dx+C is still equal to f(x).
A definite integral is the limit of a Riemann sum as the number of terms tends to infinity. It is denoted by ∫
a
b
f(x)dx, where a and b are the limits of integration. A definite integral does not have an arbitrary constant of integration, because the limits of integration specify a unique value for the integral.
In other words, an indefinite integral is a family of functions that share the same derivative, while a definite integral is a single number.
A private museum charges $40 for a group of 10 or fewer people. A group consisting of more than 10 people must, in
addition to the $40, pay $2 per person for the number of people above 10. For example, a group of 12 pays $44. The
maximum group size is 50.
a) How much does a group of 16 pay?
b) Find a formula for the cost function.
c) What are the domain and range of the cost function? (Hint: Use the graph on the calculator)
Answers
Answer:
i hope this helpes
Step-by-step explanation:
a) A group of 16 pays $40 + ($2 x (16 - 10)) = $40 + $6 = $46.
b) The cost function can be represented as C(x) = 40 + 2(x - 10) for x > 10 and C(x) = 40 for x <= 10, where x is the number of people in the group and C(x) is the cost for the group.
c) The domain of the cost function is all non-negative real numbers less than or equal to 50 (0 <= x <= 50), since the maximum group size is 50. The range of the cost function is all non-negative real numbers greater than or equal to 40 (C(x) >= 40), since the minimum charge for a group is $40.
Answer:
a) $52
b) C(x) = 40 + 2x, if x > 10 and x ≤ 50
C(x) = 40, if x ≤ 10
c) Domain = {x ≥ 1 and x ≤ 50}
Range = { from 40 to 140}
If the value of 34÷x is a whole number, which number is the value of x ?
Answers
Answer:
1 , 2 , 17 or 34
Step-by-step explanation:
34 can divide by these numbers and still be a whole number
hope this helps...
Mila's math teacher said that each question answered correctly on a test would be worth 3 points. Answer the questions below regarding the relationship between the number of questions correct and the score on the test.
Answers
After answering the presented question, we can conclude that probability Therefore, the probability of 30 or more seconds between vehicle arrivals is approximately 0.0498.
What is probability?Probability is a measure of how likely an event is to occur. It is represented by a number between 0 and 1, with 0 representing a rare event and 1 representing an inescapable event. Switching a fair coin and coin flips has a chance of 0.5 or 50% because there are two equally likely outcomes. (Heads or tails). Probabilistic theory is an area of mathematics that studies random events rather than their attributes. It is applied in many fields, including statistics, economics, science, and engineering.
Sketch of exponential probability distribution with mean of 12 seconds:
|
|
| .
| . .
| . .
| . .
| . . .
| . . .
| . . .
| . . .
| . . .
| . . . .
| . . . .
| . . . .
| . . . . .
| . . . . .
|_____________. . . . . . .
0 12 X
The X-axis represents the time between vehicle arrivals, and the Y-axis represents the probability density. The peak of the distribution is at 12 seconds, which is the mean.
b. Probability of the arrival time between vehicles being 12 seconds or less:
Since the mean of the exponential distribution is 12 seconds, we can use the cumulative distribution function (CDF) to find the probability of the arrival time being 12 seconds or less:
\(P(X < = 12) = 1 - e^(-12/12) = 1 - e^(-1) ≈ 0.6321\)
Therefore, the probability of the arrival time between vehicles being 12 seconds or less is approximately 0.6321.
c. Probability of the arrival time between vehicles being 6 seconds or less:
\(P(X < = 6) = 1 - e^(-6/12) = 1 - e^(-0.5) ≈ 0.3935\)
Therefore, the probability of the arrival time between vehicles being 6 seconds or less is approximately 0.3935.
d. Probability of 30 or more seconds between vehicle arrivals:
\(P(X > = 30) = e^(-30/12) ≈ 0.0498\)
Therefore, the probability of 30 or more seconds between vehicle arrivals is approximately 0.0498.
To know more about probability visit:
https://brainly.com/question/11234923
#SPJ1
Please anyone that can help me

Answers
Answer:
\(|\frac{x}{y} |\)
Step-by-step explanation:
Pre-SolvingWe are given the following expression: \(\sqrt\frac{x^3y^5}{xy^7}\), where x > 0 and y > 0.
We want to simplify it.
To do that, we can first simplify what is under the radical, then take the square root of what is left.
Recall that when simplifying exponents, we don't want any negative or non-integer radicals left.
SolvingTo simplify what is under the radical, we can remember the rule where \(\frac{a^n}{a^m} = a^{n-m}\).
So, that means that \(\frac{x^3}{x} = x^2\) and \(\frac{y^5}{y^7} = y^{-2}\) .
Under the radical, we now have:
\(\sqrt{x^2y^{-2}}\)
Now, we take the square root of both exponents to get:
\(|xy^{-1}|\)
The reason why we need the absolute value signs is because we know that x > 0 and y > 0, but when we take the square root of of \(x^2\) and \(y^{-2}\) , the values of x and y can be either positive or negative, so by taking the absolute value, we ensure that the value is positive.
However, we aren't done yet; remember that we don't want any radicals to be negative, and the integer of y is negative.
Recall that if \(a^{-n}\), that is equal to \(\frac{1}{a^n}\).
So, by using that,
\(|x * \frac{1}{y} |\)
This can be simplified to:
\(|\frac{x}{y} |\)
What is the area of the rectangle written in simplest form
A-5/9ft
B-3/4ft
C-3ft
D-31/3ft

Answers
Answer:
ans is A
area = l*b
area=(5/6)*(4/6)=20/36=5/9
If Leila continue to eat 8 chips an hour will they ever eat the same amount of chips at the same
time? Explain your reasoning.
Answers
Answer:
Step-by-step explanation: