m^2= 100, n^2 = 400, k^2=1600. What is
the greatest value of 2m + 3n + 4k = ?
A) 270 B) 260 C) 250 D) 240
Answers
Answer:
D).
Step-by-step explanation:
usually you got = 2(10)+3(20)+4(40) =240
Related Questions
A tour bus carries tourists through a historic district in Savannah, Georgia, serving 280 customers per day. The charge is $12 per person. The owner estimates that the company will lose 16 customers a day for each $2.10 increase in the price. What charge would be most profitable for the bus company?
Answers
We have the following information:
they have 280 customers per day and they charge $12 per person. For every increase of the cost by $2.10, they loose 16 customers.
Let's calculate the earning for each price to see which one makes the most amount of money
At the original prince, 280 customers for $12 each, they will earn 280x12 which is $3,360:
For the first increase of $2.1, the cost will be:
$12+$2.1=$14.1
but they will loose 16 people, so they will have:
280-16=264 customers.
The earinings for this set up are shown in the following image:
We repeat this process adding increases of $2.1 to the cost, and decreasing the number of customers by 16:
As we can see, unitl the charge of 24.6 the earnings are still increasing, we continue the table as follows:
For the charge of $26.7, the earning now decrease. So the most profitable charge for the bus is: $24.6




on average, ruth has noticed that 19 trains pass by her house daily (24 hours) on the nearby train tracks. what is the probability that more than 4 trains will pass her house in a 4 hour time period? round the final answer to three decimal places.
Answers
The probability that more than 4 trains will pass Ruth's house in a 4-hour time period is 0.637.
To calculate this, we can first calculate the average number of trains that pass her house in one hour. Since 19 trains pass her house daily (24 hours), it is safe to assume that these trains are evenly distributed throughout the day.
Therefore, 19/24 = 0.792 trains pass her house in one hour. In 4 hours, this means that 3.168 trains would pass her house on average.
We can then use the Poisson Distribution to determine the probability of more than 4 trains in a 4 hour time period. The formula for the Poisson Distribution is P(x;λ) = (e^-λ)*(λ^x)/x!.
In this case, x = 4 and λ = 3.168. Plugging this into the equation gives us 0.637. Therefore, the probability that more than 4 trains will pass Ruth's house in a 4-hour time period is 0.637.
For more questions like Probability visit the link below:
https://brainly.com/question/13098829
#SPJ4
are there more ways to shuffle a deck of cards than atoms
Answers
There are 8.0658 × \(10^{67}\) more form to shuffle a deck of cards than atoms.
What is the factorial?
Factorial is an important function, which is used to find how many ways things can be arranged or the ordered set of numbers.The factorial of a whole number is the function that multiplies the number by number below it.
The number of ways to shuffle a deck of cards is astronomically large, far greater than the estimated number of atoms in the observable universe.
A standard deck of 52 playing cards can be arranged in 52 factorial ways, denoted as 52!. This means multiplying all the positive integers from 1 to 52 together:
52! = 52 × 51 × 50 × ... × 3 × 2 × 1=8.0658 × \(10^{67}\).
Therefore,the exact value of 52! is an large number, approximately equal to 8.0658×\(10^{67}\).
To learn more about the factorial refer here
brainly.com/question/25997932
#SPJ4

The inverse of x + y is ?
Answers
Answer:
y + x
Step-by-step explanation:
A 90% confidence interval for the mean of a population is computed to be 135 to 160. Which one of the following claims would the interval tend to refute?
A. The population mean is more than 110.
B. The population mean is less than 150.
C. The population mean is between 140 and 150.
D. The population mean is more than 140.
E. The population mean is less than than 125.
Answers
The claim that the population mean is less than 125 (Option E) would
the interval tends to refute.
How to know which claim would the interval tends to refute?The 90% confidence interval for the population mean is 135 to 160. This means that if we were to repeat the process of taking samples from the same population and constructing a 90% confidence interval, we would expect 90% of the intervals to contain the true population mean.
With this in mind, let's consider each claim:
A. The interval does not rule out the possibility that the population mean is more than 110, as 110 is less than the lower bound of the interval.
B. The interval does not rule out the possibility that the population mean is less than 150, as 150 is greater than the upper bound of the interval.
C. The interval does not rule out the possibility that the population mean is between 140 and 150, as both of these values fall within the interval.
D. The interval does not rule out the possibility that the population mean is more than 140, as 140 is less than the upper bound of the interval.
E. The interval refutes the claim that the population mean is less than 125, as 125 is less than the lower bound of the interval.
Therefore, the answer is (E) The population mean is less than than 125.
Learn more about confidence interval
brainly.com/question/24131141
#SPJ11
recursion is sometimes required to solve certain types of problems. true/false
Answers
True. Recursion is often necessary to solve certain types of problems that exhibit a recursive structure or require repeated subproblem solving.
Recursion is a programming technique where a function calls itself in its own definition. It allows for the decomposition of complex problems into smaller, more manageable subproblems that can be solved recursively. Recursion is particularly useful when problems exhibit a recursive structure, such as tree traversal, backtracking, or divide-and-conquer algorithms.
For example, problems like computing the factorial of a number, calculating Fibonacci numbers, or traversing a binary tree can be elegantly and efficiently solved using recursion. These problems can be broken down into smaller instances of the same problem until a base case is reached, and then the solutions are combined to solve the original problem.
However, it's worth noting that not all problems require recursion for their solution. There are alternative approaches, such as iterative loops or dynamic programming, which can be used depending on the problem's characteristics and requirements.
To learn more about Recursion click here, brainly.com/question/30063488
#SPJ11
Which of the following is divisible by 3?
a) 10
b) 24
c) 67
d) 555
Answers
Answer:
24, 555 are answer of this question.
Step-by-step explanation:
2+4=6 (3×8)
5+5+5=15 (15 is divisible by 3 ).
Answer:
B and D
Step-by-step explanation:
24 divided by 3 equals 8
555 divided by 3 equals 185
3 does not divide equally into 24 or 67
HOPE THIS HELPS <33333
-Silver
How many quarters are there in 7 1/2?
Answers
Answer: 30.
Step-by-step explanation:
\(7\frac{1}{2} =\frac{7*2+1}{2} \\\frac{14+1}{2}=\frac{15}{2}\\ \frac{15*2}{2*2}=\frac{30}{4} \\ \frac{30}{4}=30*\frac{1}{4} .\)
There are total 30 quarters in \(7\frac{1}{2}\).
What is one quarter?A quarter is one out of four equal parts. One quarter is the same as the fraction ¼.
What is mixed fraction?A fraction represented with its quotient and remainder is a mixed fraction.
How to convert a mixed fraction into an improper fraction?To change a mixed fraction to an improper fraction, we multiply the whole number by the denominator and then add this product with the numerator.
According to the given question.
We have a mixed fraction \(7\frac{1}{2}\).
So, the improper fraction of the given mixed fraction is given by
\(7 \frac{1}{2} = \frac{15}{2}\)
To find the number of quarters in the given mixed fraction, we will divide \(7\frac{1}{2}\) by \(\frac{1}{4}\).
Therefore,
\(\frac{7\frac{1}{2} }{\frac{1}{4} }\)
= \(\frac{\frac{15}{2} }{\frac{1}{4} }\)
\(= \frac{15\times 4}{2}\)
\(= 15\times 2\)
\(= 30\)
Hence, there are total 30 quarters in \(7\frac{1}{2}\).
Find out more information about mixed fraction and quarters here:
https://brainly.com/question/24486558
#SPJ2
I need help!!!!, I’m struggling

Answers
Answer:
4yft57
Step-by-step explanation:
bc i said so
the plane of a room is shown in the picture. the scale is 2 inches: 6 feet. what is the actual length of the room?
what is the actual width of the room? what is the actual area of the room?
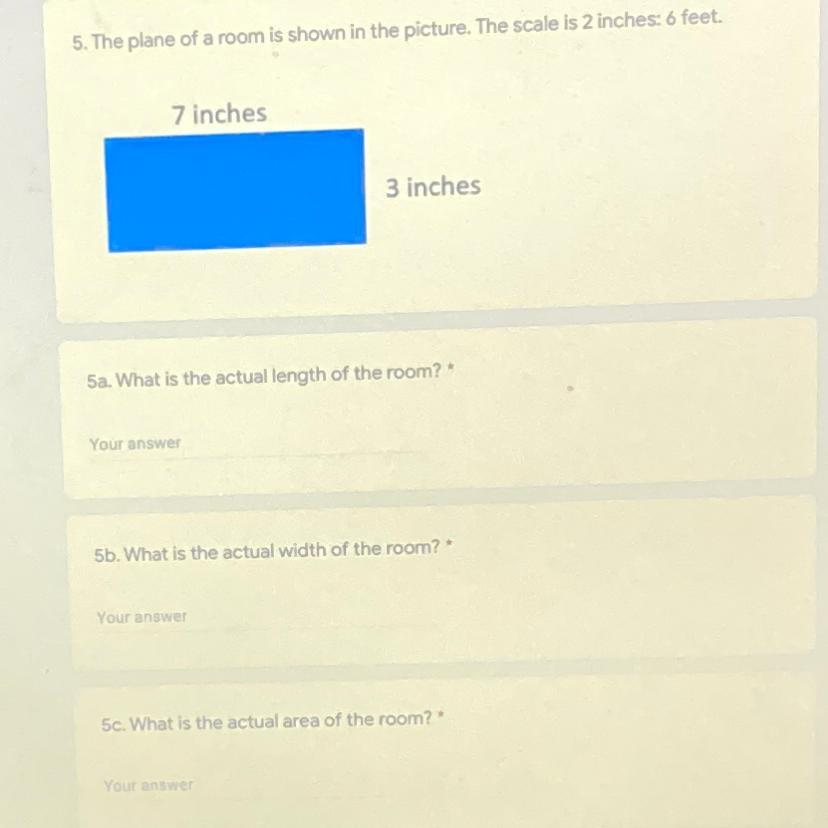
Answers
Since 2 inches = 6 ft and length of room in the place = 7 inches,
(2x3.5) inches = 6x3.5 ft
7 inches = 21ft
Actual Length of Room = 21 ft.
Width of Room in plane = 3 inches
(2x1.5) inches = 6 x 1.5 ft
= 9 ft
Actual Length of Rook = 9 ft.
Actual Area of Room = Actual Length of Room x Actual Width of Room = 21 x 9 = 189 ft^2
two fair dice, each with at least 6 faces are rolled. on each face of each dice is printed a distinct integer from 1 to the number of faces on that die, inclusive. the probability of rolling a sum of 7 is 3 4 of the probability of rolling a sum of 10, and the probability of rolling a sum of 12 is 1 12 . what is the least possible number of faces on the two dice combined?
Answers
Using the Counting the faces of two dice,
the atleast 17 number of faces are possible on the combination of two dice.
First, we have to count the favorable cases,
We know both dice have atleast 6 faces.
It gives 6 favorable cases for a sum of 7.
If we can count them if mean even if dice had more than 6 faces, will matter of for sum of 7.
Now, the mean, we need 6× 4/3=8 (favorable cases for the sum of 10)
If we count 3 favorable cases for each having 6 faces.
For more than 9 faces on a dice matter give the denominator (sample space) are the same for both sum of 7 and the sum of 10, and the probability of one is in proportion to the other.
It mean, additional 5 cases must be ( 7,2), (2,7), (8,2), (2,8) ,(9,1)
So , one of the dice has 8 faces and the other has atleast 9 faces.
Now, we must have atleast 17 combined faces of two dice for probability . So, we get if 12 with configration of 8 faces on one dice.
To learn more about Counting faces of combined dice, refer:
https://brainly.com/question/1302068
#SPJ4
consider running golden section search on a function that is unimodal. if the method starts with an initial bracket of , what is the length of the bracket after 1 iteration?
Answers
The length of the bracket after 1 iteration is 100%.
Let f(x) = x³-15x² + 50x
a = 0, b=10.
Let the golden ratio be
GR=√5-1 / 2=0.618
Now, d = GR (b-a)
= 0.618 (10-0) = 6·18
\(x_{1}\)= a+d = 0 + 6·18 = 6.18
\(x_{2}\) = b-d = 10- 6·18 = 3.82
f(\(x_{1}\)) = (6·18)³ - 15 (6·18)² + 50(6·18) = -27.887
f(\(x_{2}\)) = (3.82)³-15(3.82)²+50(3.82)=27.857
so, f(\(x_{2}\)) > f(\(x_{1}\)) new interval is [a,x,]
i.e., maximum lies in [0, 6·18]
so, Xmax = \(x_{2}\)= 382
Uncertainty in measurement will be,
∈= \(\frac{1-GR) (b-a)}{Xopt}\) =\(\frac{((1-0.618) X (10-0)}{382}\) × 100%
∈ = 100%
In arithmetic, quantities are within the golden ratio if their ratio is the same as the ratio in their sum to the larger of the 2 portions. Expressed algebraically, for quantities a and b with \(a > b > 0\), \(\frac{(a+b)}{a}\) = \(\frac{a}{b}\)= φ
The golden ratio turned into known as the acute and suggest ratio by way of Euclid, and the divine proportion using Luca Pacioli, and also is going through numerous other names. The golden ratio seems in some patterns in nature, such as the spiral association of leaves and different elements of plants.
A few twentieth-century artists and architects, together with Le Corbusier and Salvador Dalí, have proportioned their works to approximate the golden ratio, believing them to be aesthetically appealing. these uses often appear in the form of a golden rectangle.
To learn more about the Golden Ratio visit here:
brainly.com/question/12450159
#SPJ4

8. (10 points) Describe the level surfaces of the function. Consider all the cases for k. (b) f(x, y, z)=x²- y2-23 (x, y, z)=-x’+y
Answers
To describe the level surfaces of the function f(x,y,z) = x² - y² - 23, we need to find the values of k for which f(x,y,z) = k.
So, let's consider the cases for k:
Case 1: k > 23
If k > 23, then f(x,y,z) = x² - y² - 23 > 0 for all (x,y,z) in R³. Therefore, there are no level surfaces for k > 23.
Case 2: k = 23
If k = 23, then f(x,y,z) = x² - y² - 23 = 0 is the equation of a hyperboloid of two sheets, centered at the origin, with its axis along the y-axis. This is because the signs of x² and y² are opposite, and the constant term is negative.
Case 3: -23 < k < 23
If -23 < k < 23, then f(x,y,z) = x² - y² - 23 = k is the equation of a hyperboloid of one sheet, centered at the origin, with its axis along the y-axis. This is because the signs of x² and y² are opposite, but the constant term is negative.
Case 4: k = -23
If k = -23, then f(x,y,z) = x² - y² - 23 = 0 is the equation of a single point at the origin.
Case 5: k < -23
If k < -23, then f(x,y,z) = x² - y² - 23 < 0 for all (x,y,z) in R³. Therefore, there are no level surfaces for k < -23.
In summary, the level surfaces of f(x,y,z) = x² - y² - 23 are:
For k > 23, there are no level surfaces.For k = 23, the level surface is a hyperboloid of two sheets.For -23 < k < 23, the level surface is a hyperboloid of one sheet.For k = -23, the level surface is a single point at the origin.For k < -23, there are no level surfaces.Visit here to learn more about hyperboloid brainly.com/question/30640566
#SPJ11
what is the answer for , 5ײ + 1 + × + 3ײ
Answers
Explanation:
-collect like terms. We have 5x^2 and 3x^2. Add those two and then rewrite the equation in quadratic form. So the answer is 8x^2+x+1
Find parametric equations and a parameter interval for the motion of a particle in the xy plane that traces the ellipse 16x^2+9y^2=144 once counterclockwise.
Answers
The parametric equations for the motion of the particle in the xy plane that traces the counterclockwise ellipse are x = 6cos(t) and y = 4sin(t), where t is the parameter. The parameter interval for the motion is 0 ≤ t ≤ 2π.
To find the parametric equations for the counterclockwise motion of the particle along the given ellipse, we can start by parameterizing the ellipse equation \(16x^2 + 9y^2 =\) 144. We divide both sides of the equation by 144 to normalize it, giving us \((x^2/9) + (y^2/16\)) = 1. By comparing this equation with the standard form of an ellipse, we can see that a = 3 and b = 4.
We can then use the trigonometric parametrization of an ellipse to obtain the parametric equations. Letting x = acos(t) and y = bsin(t), where t is the parameter, we substitute the values for a and b, resulting in x = 6cos(t) and y = 4sin(t). These equations represent the motion of the particle along the ellipse.
Since we want the particle to trace the ellipse counterclockwise, we need to cover the full circumference of the ellipse. This corresponds to a parameter interval of 0 ≤ t ≤ 2π, which completes one full revolution around the unit circle. Therefore, the parametric equations for the motion of the particle are x = 6cos(t) and y = 4sin(t), with a parameter interval of 0 ≤ t ≤ 2π.
Learn more about trigonometric here:
https://brainly.com/question/29024806
#SPJ11
What is an equation of the line that passes through the point ( − 2 , − 6 ) and is parallel to the line x + 2 y = 8 ?
Answers
The line parallel to the line x + 2y = 8 is y = -(1/2)x - 7 Or (1/2)x + 7 = - 7.
What is slope?The slope is the rate of change of the y-axis with respect to the x-axis.
The equation of a line in slope-intercept form is y = mx + b, where
slope = m and y-intercept = b.
We know the greater the absolute value of a slope is the more steeper is it's graph or rate of change is large.
The given line is x + 2y = 8 ⇒ 2y = - x + 8 ⇒ y = -(1/2)x + 8.
We know line parallel to each other have the same slope and it passing through (-2, - 6).
∴ - 6 = -(1/2)(-2) + b.
- 6 = 1 + b.
b = - 7.
So, The required line is y = -(1/2)x - 7.
learn more about lines here :
https://brainly.com/question/2696693
#SPJ1
Please help me. I really appreciate it if you answered. Thank you! <3
Mr. Brownwood invests a certain amount of money at 9% interest and $1,800 more than that amount in another account at 11% interest. At the end of one year, he earned a total of $818 in interest. How much money was invested in each account?
$3,500 at 9%;
$4,300 at 11%
$3,100 at 9%;
$4,900 at 11%
$3,400 at 9%;
$3,200 at 11%
Answers
Answer:
$3100 is invested at 9%
$4900 is invested at 11%
Step-by-step explanation:
Let's take "x" be the amount invested at 9%.
(x + 1800) is invested in another account at 11%.
The interest amount earned by the two accounts is $818.
Here we can use the simple interest formula and find the amount invested in each account.
Simple interest (I) = , where P- is the principal , N is the number of years and R is the interest rate.
Simple interest =
0.09x + 0.11(x+1800) = 818
Now we have to simplify and find the value of x .
Use the distributive property and simplify the second term.
0.09x + 0.11x + 198 = 818
0.2x + 198 = 818
0.2x =818 - 198
0.2x = 620
x = 620/0.2
x = 3100.
So $3100 is invested at 9%
x + 1800 = 3100 + 1800
= $4900
$4900 is invested at 11%
Hope this helped.
Besides being simple for its own sake, what other advantage do simple models usually have?
a) Higher accuracy
b) Greater complexity
c) Easier interpretation
d) More detailed predictions
Answers
The correct option is c) Easier interpretation. One of the main advantages of simple models is their ease of interpretation. Simple models tend to have fewer parameters and less complex mathematical equations, making it easier to understand and interpret how the model is making predictions.
This interpretability can be valuable in various domains, such as medicine, finance, or legal systems, where it is important to have transparent and understandable decision-making processes.
Complex models, on the other hand, often involve intricate relationships and numerous parameters, which can make it challenging to comprehend the underlying reasoning behind their predictions. While complex models can sometimes offer higher accuracy or make more detailed predictions, they often sacrifice interpretability in the process.
To know more about complex visit-
brainly.com/question/28235673
#SPJ11
How do you solve this?!!

Answers
Answer:
I dont know try asking ur parents (I'm so sry that sounded mean)
Let X represent the full height of a certain species of tree. Assume that X has a normal probability distribution with = 36.1 ft and o- 6.8 ft. You intend to measure a random sample of n = 81 trees. What is the mean of the distribution of sample means? the What is the standard deviation of the distribution of sample means (i.e., the standard error in estimating the mean)? (Report answer accurate to 4 decimal places.) σ= Tip: Use the Desmos calculator...
Answers
The standard deviation of the distribution of sample means, or the standard error in estimating the mean, is approximately 0.7569 ft, rounded to 4 decimal places.
To find the mean of the distribution of sample means, we use the formula:
Mean of sample means = Mean of the population
In this case, the mean of the population is given as μ = 36.1 ft.
Therefore, the mean of the distribution of sample means is also 36.1 ft.
To find the standard deviation of the distribution of sample means, also known as the standard error, we use the formula:
Standard error = Standard deviation of the population / √(Sample size)
In this case, the standard deviation of the population is given as σ = 6.8 ft, and the sample size is n = 81.
Plugging in these values into the formula, we have:
Standard error = 6.8 / √(81)
Calculating this expression, we find:
Standard error ≈ 0.7569
Therefore, the standard deviation of the distribution of sample means, or the standard error in estimating the mean, is approximately 0.7569 ft, rounded to 4 decimal places.
To know more about standard deviation, visit:
https://brainly.com/question/13899066
#SPJ11
ANSWER FOR 74 POINTS !!!
Belinda is thinking about buying a house for $249,000. The table below shows the projected value of two different houses for three years:
Number of years 1 2 3
House 1 (value in dollars) 253,980 259,059.60 264,240.79
House 2 (value in dollars) 256,000 263,000 270,000
Part A: What type of function, linear or exponential, can be used to describe the value of each of the houses after a fixed number of years? Explain your answer.
(2 points)
Part B: Write one function for each house to describe the value of the house f(x), in dollars, after x years. (4 points)
Part C: Belinda wants to purchase a house that would have the greatest value in 45 years. Will there be any significant difference in the value of either house after 45 years? Explain your answer, and show the value of each house after 45 years. (4 points)
Answers
House 2's value, on the other hand, is increasing at a steady rate throughout time because it has a linear growth rate.
what is exponential function ?A mathematical function with the formula f(x) = abx, where "a" and "b" are constants and "x" is a variable, is an exponential function. The exponent "x" can be any real integer, whereas the base "b" is often a positive real number higher than 1.Exponential functions are frequently used to describe phenomena like population expansion, radioactive substance decay, and disease spread that increase or decrease over time at a constant percentage rate. In these circumstances, the function's present value determines how quickly it will grow or decay.
given
F(x) = 249,000 * 1.017 for House 1.
F(x) = 249,000 + 7,000x for House 2.
Part C:
The functions we discovered in Part B can be changed to x = 45 to determine the worth of each residence after 45 years.
f(45) = 249,000 * 1.017 * 45 = 1,281,926.69 for House 1.
f(45) = 249,000 + 7,000(45) = 579,000 for House 2.
As we can see, after 45 years, the value of each residence has significantly changed.
This is as a result of House 1's exponential growth rate, which causes a rapid rise in value over time.
House 2's value, on the other hand, is increasing at a steady rate throughout time because it has a linear growth rate.
To know more about Exponential Function here:
brainly.com/question/14355665
#SPJ1
Someone please help me

Answers
Answer: csc -675 = √2
Step-by-step explanation:
Keep adding 360 to find your reference angle.
-675 + 360 = -315
-315 + 360 = 45
Your reference angle is 45°
csc 45 = \(\frac{1}{sin 45}\)
Remember your unit circle:
sin 45 = \(\frac{\sqrt{2} }{2}\)
Substitute:
csc 45 = \(\frac{1}{\frac{\sqrt{2} }{2}}\) >Keep change flip
csc 45 = 2/√2 >Get rid of root on bottom
csc 45 = \(\frac{2\sqrt{2} }{2}\)
csc 45 = √2
csc -675 = √2
draw a coordinate plane and find points A(-2;0) B(1;4) C(-5;-1) D(5;0) E(0;0)
pls help me
20 points
Answers

What is the solution(s) to the equation 5a2 - 44 = 81?
A
+25
B
-5
55
D
1125
Answers
Answer:
B
Step-by-step explanation:
5a^2 - 44 = 81 Add 44 to both sides
5a^2 = 81 + 44 Collect like terms
5a^2 = 125 Divide both sides by 5
a^2 = 125/5
a^2 = 25 Take the square root of both sides
√a^2 = √25
a = +5
a = -5
The answer is B
A hair cut cost $25 and you want to leave a 15% tip what is the total bill?
Answers
HELP PLEASEEEEEEE!!!!!!!!!!!!!!!!

Answers
What number can add of 7 to equal to 9? It's 2 because 2+7=9
Help someone that’s good at math need your help 15 points !

Answers
Answer:
4x-4+3
Step-by-step explanation:
Answer:
-4+4x=3
Step-by-step explanation:
So the first step is to derive an equation from the model.
There are 4 positive x and 4 negative 1 which equal 3 positive 1 which should look like:
4x-4=3
which could be rewritten as:
-4+4x=3
Given: D is the midpoint of AB; E is the midpoint of AC.
Prove: DE BC
y
Complete the missing parts of the paragraph proof.
Proof:
To prove that DE and BC are parallel, we need to show
that they have the same slope.
slope of DE = 12-11=_C-C
X2 - x1 a + b - b
A(2b, 2c)
D(b, c)
Ela + bc)
slope of BC =
B(0,0)
C(2a, 0)
Therefore, because
DE 1 BC.

Answers
Answer:
The lines DE and BC have the same slope, therefore the two lines, DE and BC, are parallel
Step-by-step explanation:
To prove that DE is parallel to BC, we have;
The slope, m of the lines DE and BC are found from the following equation;
\(Slope, \, m =\dfrac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
Where;
(x₁, y₁) and (x₂, y₂) = (b, c) and (a + b + c) for DE, we have;
\(Slope, \, m =\dfrac{c - c}{a + b-b} = 0\)
Where we have (x₁, y₁) and (x₂, y₂) = (0, 0) and (2a, 0) for BC, we have;
\(Slope, \, m =\dfrac{0 - 0}{2a-0} = 0\)
Therefore, because the lines DE and BC have the same slope, the two lines DE and BC are parallel.
Answer:
slope of DE = 0
slope Bc = 0
slopes are =
Step-by-step explanation:
When your measurement error is between 4.5 and 5%, the number of cases are [____]. Select the correct answer below.
400
450
500
Answers
When your measurement error is between 4.5% and 5%, the number of cases is 450.
The margin of error (MOE) is a measure of the uncertainty or statistical error in a survey's findings. When it comes to determining the survey's accuracy, the MOE is the most important consideration. When determining the sample size required to generate the lowest MOE possible, the survey creator's decision comes into play.
Let us assume that a 95 percent confidence level is used in a survey of a population. The MOE will be larger if a more rigorous confidence level is employed.
Margin of Error = (Critical Value) x (Standard Deviation) / square root of (Sample Size)
If the population size is less than 100,000, the MOE equation is usually used.
The most commonly used equation is n = (Z2 * P * Q) / E2 if the population size is greater than 100,000.
Hence, when the measurement error is between 4.5 and 5%, the number of cases is 450.
To know more about Standard Deviation visit:
https://brainly.com/question/29115611
#SPJ11
Lilly cut a piece of string that was 17 feet long.luna cut a piece of string that was 5 yards long.Lilly wanted to cut her string so that it was the same length as lunas. how many feet did she need to cut off? Plsssss help meeeeeeee
Answers
Answer:
Lilly only needed to cut off 15 feet.
Step-by-step explanation:
1 yard = 3 feet. Luna cut 5 yards, so she cut 15 feet off. Lilly, on the other hand, cut off 17 feet.