Lisa Callaghan data on the grams of fat and the grams of carbohydrates in 10 sandwiches at a popular restaurant the table below represents the data she recorded which linear equation best fits Lisa's data

Answers
Linear representation of data
All options gives values too high , except one
Because for x= 17 ,y= 31
23x17 its much bigger than 31
1.5x17 + 27 much bigger than 31
27x17 much bigger than 31
Then, only option that gives near value of 31 is
y= 0.5x + 23
because 0.5• 17 + 23 = 31.5
Then right answer is: Option A)
y = 0.5x + 23
Related Questions
a certain radioactive isotope has leaked into a small stream. one hundred days after the leak 8% of the original amount of substance remained. Determine the half life of this radioactive isotope
Answers
Answer:
The half-life of a radioactive substance is the time it takes for half of the initial amount of the substance to decay. We can use the fact that 8% of the original amount remains after 100 days to determine the half-life of the isotope.
Let's assume that the initial amount of the substance is 1 unit (it could be any amount, but we're assuming 1 unit for simplicity). After one half-life, half of the original amount remains, or 0.5 units. After two half-lives, half of the remaining amount remains, or 0.25 units. After three half-lives, half of the remaining amount remains, or 0.125 units. We can see that the amount of substance remaining after each half-life is half of the previous amount.
We can use this information to set up the following equation:
0.08 = (1/2)^n
where n is the number of half-lives that have elapsed. We want to solve for n.
Taking the logarithm of both sides, we get:
log(0.08) = n*log(1/2)
Solving for n, we get:
n = log(0.08) / log(1/2) = 3.42
So the number of half-lives that have elapsed is approximately 3.42. Since we know that 100 days is the time for three half-lives (from the previous calculation), we can find the half-life by dividing 100 days by 3.42:
Half-life = 100 days / 3.42 = 29.2 days (rounded to one decimal place)
Therefore, the half-life of the radioactive isotope that leaked into the stream is approximately 29.2 days.
In the data set below, what is the interquartile range?
26 42 52 61 75 85 93 96
Answers
Answer:
the iqr is 42
Step-by-step explanation:
Here are the heights (in inches) of 12 students in a seminar. 71, 67, 62, 60, 70, 64, 68, 72, 58, 63, 60, 66 What is the percentage of these students who are shorter than 65 inches? 1% X 5
Answers
25% of the students in the seminar are shorter than 65 inches.
To find the percentage of students who are shorter than 65 inches, we first need to find the number of students whose height is less than 65 inches:
There are three students who are shorter than 65 inches: 62, 60, and 58.
Therefore, the percentage of students who are shorter than 65 inches is:
(3 students / 12 students) × 100% = 25%
Note that the value given for 1% × 5 does not appear to be relevant to this question, and is not necessary for the calculation of the percentage of students who are shorter than 65 inches.
For such more questions inches
https://brainly.com/question/876758
#SPJ8
PLEASE HELP i WILL MaRK BRAINLY plsssssss
A "light" popcom has 120 Calories per serving. This is 25% fewer Calories than a serving of regular popcorn. How many
Calories does each serving of regular popcom have?
175
b. 250
480
d. 160
C.
a
Answers
We're given:
The popcorn is 120 calories per serving120 calories is 25% fewer calories than original popcornWe must find the calorie count per serving of the original popcornDetermine VariablesLet x equal the calorie count per serving of the original popcorn.
Create an EquationThe light popcorn has a calorie count of 120, which is 25% fewer calories than regular popcorn. This means that 75% of the calorie count of regular popcorn is equal to that of the light popcorn:
\(x*0.75=120\)
Solve the Equation\(x*0.75=120\)
⇒ Divide both sides by 0.75:
\(\dfrac{x*0.75}{0.75}=\dfrac{120}{0.75}\\\\x=160\)
AnswerTherefore, each serving of regular popcorn has 160 calories.
A bakery is making whole-wheat bread and apple bran muffins. For each batch of break they make $35 profit. For each batch of muffins, they make $10 profit. The break takes 4 hours to prepare and 1 hour to back. The muffins take 0.5 hours to prepare and 0.5 hours to bake. The maximum preparation time available is 16 hours. The maximum bake time available is 10 hours. Let x = # of the batches of bread and y = # of batches of muffins. Outline the feasible region that can be used to find the number of batches of bread and muffins that should be made to maximize profits? Use the color RED to indicate the feasible region!
Answers
Step-by-step explanation:
let the number of wholewheat bread batches be x
let the number of muffin batches be y
prep condition: 4x + (1/2)y ≤ 16 or 8x + y ≤ 32
baking condition : 1x + (1/2)y ≤ 10 or 2x + y ≤ 20
graph each of those in the first quadrant shading in the region below each one.
Final shading is the region satisfying both conditions.
profit = 35x + 10y
allow this line to "slide" away from the origin as far as you can.
It should be clear that the farthest we can go is the intersection of
8x+y = 32 and
2x + y = 20 or the x and y intercepts of our two boundary lines.
subtract them as they are:
6x = 12
x = 2
then in our head , y = 16
max profit = 2(35) + 10(16) = 230
Just to make sure, I will test the intercepts of our intersecting region, namely (4,0) and (0,20)
for (4,0) profit = 4(35)+1 = 140
for (0,32) profit = 0 + 10(20) = 200
so max profit is 230 when x=2 and y=16
(notice all the prep time and baking time is utelized)
Sam has a deck that is shaped like a triangle with a base of 18 feet and a height of 7 feet. He plans to build a 2:5 scaled version of the deck next to his horse's water trough.
Part A: What are the dimensions of the new deck, in feet? Show every step of your work. (4 points)
Part B: What is the area of the original deck and the new deck, in square feet? Show every step of your work. (4 points)
Part C: Compare the ratio of the areas to the scale factor. Show every step of your work. (4 points)
Answers
The 2 : 5 scaled version of the deck Sam plans to build and the dimensions of the original deck indicates;
Part A; Base length of the new deck = 7.2 feet
Height of the new deck = 2.8 feet
Part B; The area of the original deck is 63 square feet
The area of the new deck is 10.08 square feet
Part C; The ratio of the areas is the square of the scale factor
What is a scale factor?A scale factor is a number or factor that is used to enlarge or reduce the dimensions a shape or size of a figure.
The base length of the triangular deck = 18 feet
The height of the triangular deck = 7 feet
The scale factor for the scaled version Sam intends to build = 2 : 5
Part A; The dimensions of the new deck are;
Base length of the new deck using the the 2 : 5 ratio is; (2/5) × 18 = 7.2 feet
The height of the new deck = (2/5) × 7 = 2.8 feet
Part B; The area of the original deck = (1/2) × 18 × 7 = 63 square feet
Area of the new dec = (1/2) × 7.2 × 2.8 = 10.08 square feet
Part C; The ratio of the areas is; 10.08/63
Ratio of the area = 10.08/63 = 4/25 = 4 : 25
The scale factor is; 2 : 5
Therefore, the ratio of the area is the square of the scale factorLearn more on scale factors here: https://brainly.com/question/28822248
#SPJ1
Enter the ordered pair for the vertices for (Ry-axis T(2, 0))(QRST).
I need help with this please help me

Answers
Answer:
Q'(-3, 5)R'(-5, -1)S'(-2, 0)T'(0, 3)Step-by-step explanation:
You want the coordinates of the vertices of QRST after it has been translated right 2 units, then reflected across the y-axis. The original coordinates are Q(1, 5), R(3, -1), S(0, 0), T(-2, 3).
Composition of TransformationsThe problem statement is written as a composition of the transformations Ry and T(2,0). A composition of functions is generally executed right to left, meaning the translation will be done first, then the reflection.
TranslationThe numbers in the translation vector are added to the coordinates:
(x, y) ⇒ (x+2, y+0)
ReflectionReflection over the y-axis changes the sign of the x-coordinate:
(x, y) ⇒ (-x, y)
ApplicationThen the composition of transformations is ...
(x, y) ⇒ (-(x+2), y)
Q(1, 5) ⇒ Q'(-3, 5)
R(3, -1) ⇒ R'(-5, -1)
S(0, 0) ⇒ S'(-2, 0)
T(-2, 3) ⇒ T'(0, 3)
find j(3x^4y^7) if j(n)=n^3
Answers
Answer:
Step-by-step explanation:
Rearrange the equation by subtracting what is to the right of the equal sign from both sides of the equation :
3*x-(4*y-7)=0
STEP
1
:
Equation of a Straight Line
1.1 Solve 3x-4y+7 = 0
Tiger recognizes that we have here an equation of a straight line. Such an equation is usually written y=mx+b ("y=mx+c" in the UK).
"y=mx+b" is the formula of a straight line drawn on Cartesian coordinate system in which "y" is the vertical axis and "x" the horizontal axis.
In this formula :
y tells us how far up the line goes
x tells us how far along
m is the Slope or Gradient i.e. how steep the line is
b is the Y-intercept i.e. where the line crosses the Y axis
The X and Y intercepts and the Slope are called the line properties. We shall now graph the line 3x-4y+7 = 0 and calculate its properties
Graph of a Straight Line :
Calculate the Y-Intercept :
Notice that when x = 0 the value of y is 7/4 so this line "cuts" the y axis at y= 1.75000
y-intercept = 7/4 = 1.75000
Calculate the X-Intercept :
When y = 0 the value of x is -7/3 Our line therefore "cuts" the x axis at x=-2.33333
x-intercept = -7/3 = -2.33333
Calculate the Slope :
Slope is defined as the change in y divided by the change in x. We note that for x=0, the value of y is 1.750 and for x=2.000, the value of y is 3.250. So, for a change of 2.000 in x (The change in x is sometimes referred to as "RUN") we get a change of 3.250 - 1.750 = 1.500 in y. (The change in y is sometimes referred to as "RISE" and the Slope is m = RISE / RUN)
Slope = 1.500/2.000 = 0.750
Geometric figure: Straight Line
Slope = 1.500/2.000 = 0.750
x-intercept = -7/3 = -2.33333
y-intercept = 7/4 = 1.75000
Enter your answer in the box. Round your final answer to the nearest degree. B 6cm, A 8cm, C
Answers
The measure of Angle C is approximately 26°.
A, B, C are vertices of a triangle, where AB = 8 cm, BC = 6 cm. To determine the measure of angle C, we need to use the cosine rule.
The cosine rule states that the square of one side of a triangle is equal to the sum of the squares of the other two sides minus twice the product of the other two sides and the cosine of the angle between them.
Mathematically, we can represent it as follows:a² = b² + c² - 2bc cos(A)where a is the side opposite to angle A, b is the side opposite to angle B, c is the side opposite to angle C.
In this case, we have AB = c = 8 cm, BC = a = 6 cm, and AC = b. We need to find the measure of angle C, which is represented as cos(C).
Using the cosine rule, we can write the equation as follows:$$\begin{aligned} b^2 &= c^2 + a^2 - 2ca\cos(C) \\ \Right arrow b^2 &= 8^2 + 6^2 - 2 \times 8 \times 6 \cos(C) \\ \Right arrow b^2 &= 64 + 36 - 96 \cos(C) \\ \Right arrow b^2 &= 100 - 96 \cos(C) \end{aligned}$$We know that b is a positive length. Hence, b² > 0 or 100 - 96 cos(C) > 0. Solving for cos(C),
we get: cos(C) < 100/96cos(C) < 1.0417Using a calculator, we can determine the inverse cosine of 1.0417 as:cos⁻¹(1.0417) = 0.4569 radians = 26.201° (rounded to the nearest degree)
Therefore, the measure of angle C is approximately 26°.
For more questions on Angle .
https://brainly.com/question/30759856
#SPJ8
What is the answer to question C?

Answers
Answer:
B
Step-by-step explanation:
The points are too scattered to determine any correlation.
Answer:
Diagram B
Step-by-step explanation:
Visually inspecting the three scatterplots, the line of best fit does not accurately fit the points on the second graph. Hence, line of best fit should not have been drawn for the second graph as the relationship isn't linear.
The line of best fit minimizes the sum of the square of the mean distance between each point. Hence, the distance between the line and the best fit line should be as small as possible.
However, the second graph isn't linear, hence , a linear line cannot model the relationship.
The sum of 2 times p and 2 is 48. What is p?
Answers
Answer:
p = 23
Step-by-step explanation:
2p + 2 = 48
-2 -2
2p = 46
/2 /2
p = 23
Hope this helps and I hope u have an Amazing day!!
2x + 3 ≥ 6 illustrat in number line
Answers
Answer:
2x + 3 ≥ 6
2x + 3 - 3 ≥ 6 - 3
2x ≥ 3
2x ÷ 2 ≥ 3 ÷ 2
x ≥ 1.5

Here are the approximate populations of three countries, expressed in scientific notation: Panama- 4x10^6 Peru- 3.2x10^7 Thailand- 7x10^7
b) Plot and label the three countries’ populations on the number line. Make sure to label each tick mark as a multiple of 10
c) Which power of 10 could you use to label the furthest right box on the number line so that all three countries' population fit?

Answers
The answers for the following questions are given below.
What is scientific notation?Scientific notation, also known as standard form or exponential notation, is a way of writing numbers that are either very large or very small in a compact and convenient way.
It is commonly used in mathematics, science, engineering, and other fields that deal with very large or very small quantities.
In scientific notation, a number is expressed as a product of a decimal number between 1 and 10 (the significand or mantissa) and power of 10.
b) To plot the populations of the three countries on a number line, we can use a logarithmic scale, which will allow us to represent the large differences in population size on a smaller scale. We can start by marking each power of 10 on the number line and then placing the populations of each country accordingly:
|-----------------|------------------|------------------|------------------|------------------|
10⁰ 10¹ 10² 10³ 10⁴
Panama: 4x10⁶ Peru: 3.2x10⁷ Thailand: 7x10⁷
c) To label the furthest right box on the number line so that all three countries' population fit, we need to find the largest population value among the three countries and then round it up to the nearest power of 10. The largest population value among the three countries is 7x10⁷, so we can round it up to 10⁸. Therefore, we can label the furthest right box on the number line as 10⁸.
To know more about number line visit:
https://brainly.com/question/28368609
#SPJ1
Populations on the number line,
B. Panama: 4x10⁶
Peru: 3.2x10⁷
Thailand: 7x10⁷
C. We can label the furthest right box on the number line as 10⁸.
What is scientific notation?Scientific notation, also known as standard form or exponential notation, is a method of writing very large or very small numbers in a compact and convenient manner.
It is widely used in mathematics, science, technology, and other disciplines that deal with very large or extremely small quantities.
A number is expressed in scientific notation as the product of a decimal number between 1 and 10 (the significand or mantissa) and a power of ten.
B). To compass the populations of the three countries on a number line, we can use a logarithmic scale, which will allow us to represent the large differences in population size on a lower scale. We can start by marking each power of 10 on the number line and also placing the populations of each country consequently .
|-----------------|------------------|------------------|------------------|------------------|
10⁰ 10¹ 10² 10³ 10⁴
Panama: 4x10⁶ Peru: 3.2x10⁷ Thailand: 7x10⁷
C). To label the rightmost box on the number line for the populations of all three countries, we need to find the largest population value among the three countries and round it up to the nearest power of ten. The maximum population of the three countries is 7x10⁷, so we can round up to 10⁸. So we can represent the rightmost box on the number line as 10⁸.
To know more about number line, visit:
brainly.com/question/28368609
#SPJ1
Which of the following is NOT a procedure for determining whether it is reasonable to assume that sample data are from a normally distributed population? Choose the correct answer below /08/19 1:59pm 3/15/19 1:59pm O A. Identifying outliers O B. Checking that the probability of an event is 0.05 or less OC. Visual inspection of a histogram to see if it is roughly bell-shaped OD. Constructing a graph called a normal quantile plot 1/29/19 1:59pm
Answers
Therefore , the solution of the given problem of probability comes out to be (B) Verifying that an event's chance is 0.05 or less is the right response.
What is probability exactly?The primary goal of a procedure's criteria-based methods is to calculate the probability that a statement is true or that a specific occurrence will occur. Any number range from 0 to 1, where 0 usually represents the likelihood of something happening and 1 typically represents an amount of confidence, can be used to represent chance. A probability illustration displays the possibility that a specific event will take place.
Here,
Several techniques can be used to determine whether it is reasonable to infer that sample data come from a population with a normally distributed population, including:
A. Recognizing anomalies
B. Verifying that an event's probability is 0.05 or lower C.
Examining a histogram visually to see if it approximately resembles a bell shape
D. Creating a normal quantile plot, a type of graph.
Option B is invalid because it doesn't reveal anything about how the sample data are distributed.
The threshold for statistical significance is the chance of an event being 0.05 or less, but it has no bearing on the distribution's shape.
As a result, (B) Verifying that an event's chance is 0.05 or less is the right response.
To know more about probability visit:
https://brainly.com/question/11234923
#SPJ1
All numbers that have 5 as a factor also have 2 as a factor.
O A. True
OB. False
Answers
The statement that all numbers that have 5 as a factor also have 2 as a factor is false, as numbers ending in 5 have five as a factor but are odd numbers, meaning that they do not have two is a factor.
What are the factors of a number?The factors of a number are the numbers by which the number is divisible.
Hence the numbers that have 2 and 5 as factors as the multiples, given as follows:
Multiples of 2: {0, 2, 4, ..., } -> all even numbers.Multiples of 5: {0, 5, 10, ...} -> all numbers finishing in 0 or 5.Numbers that finish in 5 are odd, meaning that they do not have 2 is a factor, hence the statement is false.
More can be learned about the factors of a number at https://brainly.com/question/219464
#SPJ1
Which of the following equations demonstrate that the set of polynomials is
not closed under the certain operations?
A. Subtraction: (3x^4+x^3)-(-2x^4+x^3)=5x^4
B. Addition: (x^2+x)+(x+1)=x^2+2x+1
C. Division: (x^2-5x+3)÷(x-2)=x-3+-3/x-2
D. Multiplication: (x^2-5x+3)(x-5)=x^3-10x^2+28x-15
Answers
9514 1404 393
Answer:
C. Division: (x^2-5x+3)÷(x-2)=x-3+-3/x-2
Step-by-step explanation:
The set of polynomials is closed under all basic arithmetic operations except division. The reciprocal of a (non-constant) polynomial is not a polynomial.
The division example shown in choice C illustrates the set is not closed under division.
you have 4 blue,2 black,1 white,1 red,and 2 green shirts what's the probability of not
choosing a black shirt
Answers
Answer:
60 percent, or 6/10
Step-by-step explanation:
Equation for geometric sequence 6,12,24,48,96
Answers
Answer:
a(n)=6*2^(n-1)
Step-by-step explanation:
a(n)=a(1)r^(n-1)
a(1) = 6
a(2)=6r^1=12
r=2
a(n)=6*2^(n-1)
This is a geometric sequence since there is a common ratio between each term. In this case, multiplying the previous term in the sequence by
2
2
gives the next term. In other words,
a
n
=
a
1
⋅
r
n
−
1
a
n
=
a
1
⋅
r
n
-
1
.
Geometric Sequence:
r
=
2
r
=
2
This is the form of a geometric sequence.
a
n
=
a
1
r
n
−
1
a
n
=
a
1
r
n
-
1
Substitute in the values of
a
1
=
6
a
1
=
6
and
r
=
2
r
=
2
.
a
n
=
(
6
)
⋅
(
2
)
n
−
1
a
n
=
(
6
)
⋅
(
2
)
n
-
1
Remove parentheses.
a
n
=
6
⋅
2
n
−
1
what is y is 6y=42. please i need help
Answers
Answer:
7
Step-by-step explanation:
do you really need help
..............
so why I have to wait for 12 min
\( \huge \boxed{\mathbb{QUESTION} \downarrow}\)
6y = 42, find y.\( \large \boxed{\mathfrak{Answer \: with \: Explanation} \downarrow}\)
\( \tt \: 6 y = 42\)
Divide both sides by 6.
\( \tt \: y=\frac{42}{6} \\ \)
Divide 42 by 6 to get 7.
\( \boxed{ \boxed{ \bf \: y = 7}}\)
What percent of the front page is taken up by the
prom story, including the prom photograph?
A. 20%
B. 22%
C. 25%
D. 45%
E. 60%

Answers
The percent of the front page taken up by the prom story is 20%
Calculating the percent of the front page taken up by the prom storyFrom the question, we have the following parameters that can be used in our computation:
The front page
From the front page, we have
Area front page = 5 * 4
Area front page = 20
Also, we have
Prom = 2 * 2
Prom = 4
So, we have
Percentage = 4/20 * 100%
Evaluate
Percentage = 20%
Hence, the percent of the front page taken up by the prom story is 20%
Read more about percentage at
https://brainly.com/question/843074
#SPJ1
What is the Measure of angle AOE in the figure below?

Answers
Answer:
The answer is D: 130
Step-by-step explanation:
(3x-28) +90+(66-x) = 180
2x + 128 = 180
2x = 52
x = 26
Therefore Angle AOE = 90 + (66-26)
= 130
4 There are between 20 and 50 flags.
They can be shared equally among
2 tents or 4 tents or 5 tents.
How many flags are there?
Answers
When there are between 20 and 50 flags and they can be shared equally among 2 tents or 4 tents or 5 tents. The number of flags will be 40.
How to illustrate the information?From the information, there are between 20 and 50 flags and they can be shared equally among 2 tents or 4 tents or 5 tents.
It should be noted that this simply means that we should find the highest multiple for 2, 4, and 5 between 20 and 50. This is 40.
Therefore, the number of flags is 40.
Learn more about multiples on:
brainly.com/question/26856218
#SPJ1
\(5 {x}^{2} + 3 {x}^{2} + 6x = 3x - 6x + 9x\)
find out x please fast please fast
Answers
Answer:
\(5 {x}^{2} + 3 {x}^{2} + 6x = 3x - 6x + 9x \\ 8 {x}^{2} + 6x = - 3x + 9x \\ 8 {x}^{2} + 6x = 6x \\ 8 {x}^{2} = 6x - 6x \\ 8 {x}^{2} = 0 \\ x = 0 \\ thank \: you\)
help please, the question in the picture
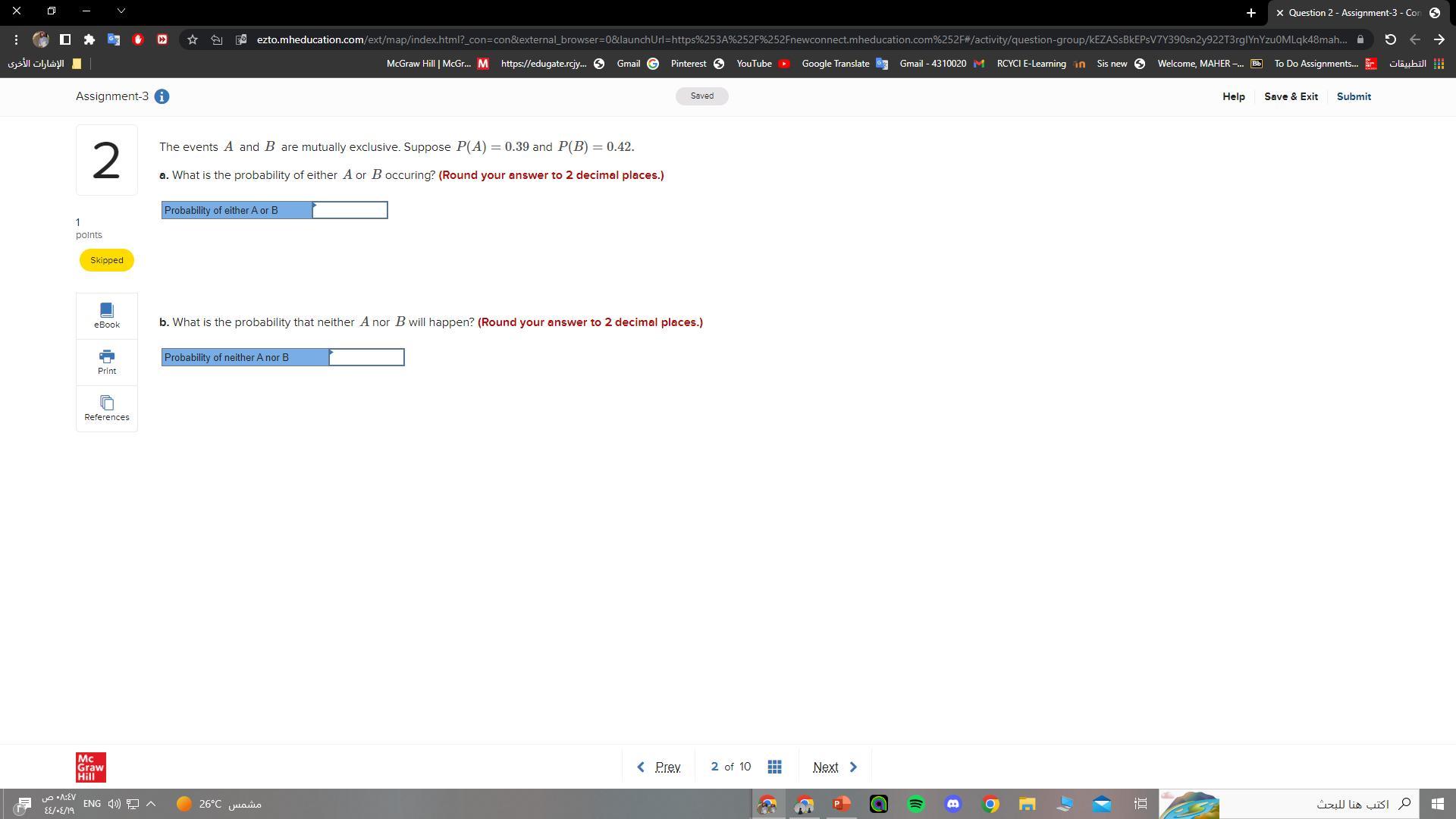
Answers
The probability of either A or B is 0.48 and the probability neither A nor B would be 0.52
What is Probability?Probability defines the likelihood of occurrence of an event. There are many real-life situations in which we may have to predict the outcome of an event. We may be sure or not sure of the results of an event
probability A will occur pr(A) = 0.39, probability A will not occur pr(A') = 1 - 0.39 = 0.61,
Probability B will occur pr(B) = 0.42, probability B will not occur, pr(B') = 1 - 0.42 = 0.58
For mutually exclusive events if A will occur it means that B will not occur
So, probability either A or B is
= pr(A) x pr(B') + pr(B) x Pr(A')
= 0.39 x 0.58 + 0.42 x 0.61
= 0.4824 and to 2 decimal places the answer becomes 0.48
The probability neither A nor B is equal to 1 - 0.48 = 0.52
In conclusion the probability Either A or B will occur is 0.48 and the probability neither A nor B is 0.52
Learn more about probability: https://brainly.com/question/251701
#SPJ1
Find the length of the line joining A (3,5) and B (1,3)
Answers
Answer:
2√2 units.
Step-by-step explanation:
To find the length of the line joining points A(3, 5) and B(1, 3), we can use the distance formula. The distance formula is given by:
d = sqrt((x2 - x1)^2 + (y2 - y1)^2)
Substituting the coordinates of points A and B into the formula, we have:
d = sqrt((1 - 3)^2 + (3 - 5)^2)
= sqrt((-2)^2 + (-2)^2)
= sqrt(4 + 4)
= sqrt(8)
= 2sqrt(2)
Therefore, the length of the line joining points A and B is 2√2 units.
The function y=f(x is graphed below. What is the average rate of change of the function f(x)on the interval 0≤x≤5?

Answers
\(m = \frac{f(5) - f(0)}{5 - 0} \)
\(m = \frac{ - 10 - 10}{5} = \frac{ - 20}{5} = - 4\)
Step-by-step explanation:
the average rate of change is
(f(high interval end) - f(low interval end))/(high interval end - low interval end)
in our case here
(f(5) - f(0)) / (5 - 0)
(-10 - 10) / 5 = -20/5 = -4
Someone do this for me

Answers
The answer is as:
a) ∠M is congruent to ∠O.
b) the two triangles XYW and ZWY are congruent by angle-angle-side (AAS) congruence.
What is the congruent angle?
When two parallel lines are cut by a transversal, the angles that are on the same side of the transversal and in matching corners will be congruent.
Since ∠NLM ≅ ∠LNO and ∠OLN ≅ ∠MNL, we have:
∠NLM + ∠LNO = ∠OLN + ∠MNL (by the transitive property of angle congruence)
Therefore, ∠NLO = ∠MLN + ∠MIN
Since ∠NLO is a straight angle (180 degrees), we have:
∠NLO = ∠M + ∠O
Substituting ∠M + ∠O for ∠NLO in the previous equation, we get:
∠M + ∠O = ∠MLN + ∠MIN
Rearranging the terms, we get:
∠M - ∠MLN = ∠MIN - ∠O
Using the fact that angle M is supplementary to angle MLN (since they form a straight angle), we have:
∠M - (180 - ∠LNO) = ∠MIN - ∠O
Simplifying, we get:
∠M - ∠LNO = ∠MIN - ∠O
Since ∠OLN ≅ ∠MNI, we have:
∠LNO = ∠MIN
Substituting ∠LNO for ∠MIN in the previous equation, we get:
∠M - ∠LNO = ∠LNO - ∠O
Adding ∠O to both sides, we get:
∠M = 2∠LNO - ∠O
Therefore, ∠M is congruent to ∠O.
#6
Proof:
Since ∠1 ≅ ∠2 and ∠3 ≅ ∠4, we have:
∠1 + ∠3 = ∠2 + ∠4 (by the transitive property of angle congruence)
Therefore, ∠1 - ∠2 = ∠4 - ∠3
Using the fact that opposite angles in a parallelogram are congruent, we have:
∠YXW = ∠1 - ∠2
∠ZWY = ∠4 - ∠3
Substituting these values in the previous equation, we get:
∠YXW = ∠ZWY
Therefore, the two triangles XYW and ZWY are congruent by angle-angle-side (AAS) congruence.
Since corresponding sides of congruent triangles are congruent, we have:
XY cong ZW.
Hence, the answer is as:
a) ∠M is congruent to ∠O.
b) the two triangles XYW and ZWY are congruent by angle-angle-side (AAS) congruence.
To learn more about the congruent angle visit:
brainly.com/question/28262429
#SPJ1
THIS IS A BREAK QUESTION
what is your favorite school subject
Answers
Answer:
Art
Step-by-step explanation:
...................
Answer:
Music
Step-by-step explanation:
Have a good rest of your day!
Calculate the volume of this cylinder in terms of Pi and to the nearest hundredth

Answers
The volume of the given cylinder in terms of pi as required to be determined in the task content is; 5000 pi.
What is the volume of the given cylinder?It follows from the task content that the volume of the cylinder which is as represented is to be determined.
Since the volume of a cylinder is;
V = 2πr²h
where r = 10 and h = 25.
V = 2π × 10² × 25.
V = 5000π.
Ultimately, the volume of the given cylinder as required to be determined is; V = 5000 pi.
Read more on volume of a cylinder;
https://brainly.com/question/9554871
#SPJ1
Assumptions: Tax depreciation is straight-line over three years. Pre-tax salvage value is 25 in Year 3 and 50 if the asset is scrapped in Year 2. Tax on salvage value is 40% of the difference between salvage value and book value of the investment. The cost of capital is 20%.
Answers
Based on the given assumptions and calculations, the net present value (NPV) of the investment in the new piece of equipment is -$27,045.76, indicating that the investment is not favorable.
To calculate the after-tax cash flows for each year and evaluate the investment decision, let's use the following information:
Assumptions:
Tax depreciation is straight-line over five years.
Pre-tax salvage value is $10,000 in Year 5 and $15,000 if the asset is scrapped in Year 4.
Tax on salvage value is 30% of the difference between salvage value and book value of the investment.
The cost of capital is 12%.
Given:
Initial investment cost = $50,000
Useful life of the equipment = 5 years
To calculate the depreciation expense each year, we divide the initial investment by the useful life:
Depreciation expense per year = Initial investment / Useful life
Depreciation expense per year = $50,000 / 5 = $10,000
Now, let's calculate the book value at the end of each year:
Year 1:
Book value = Initial investment - Depreciation expense per year
Book value \(= $50,000 - $10,000 = $40,000\)
Year 2:
Book value = Initial investment - (2 \(\times\) Depreciation expense per year)
Book value \(= $50,000 - (2 \times$10,000) = $30,000\)
Year 3:
Book value = Initial investment - (3 \(\times\) Depreciation expense per year)
Book value = $50,000 - (3 \(\times\) $10,000) = $20,000
Year 4:
Book value = Initial investment - (4 \(\times\) Depreciation expense per year)
Book value \(= $50,000 - (4 \times $10,000) = $10,000\)
Year 5:
Book value = Initial investment - (5 \(\times\) Depreciation expense per year)
Book value \(= $50,000 - (5 \times $10,000) = $0\)
Based on the assumptions, the salvage value is $10,000 in Year 5.
If the asset is scrapped in Year 4, the salvage value is $15,000.
To calculate the tax on salvage value, we need to find the difference between the salvage value and the book value and then multiply it by the tax rate:
Tax on salvage value = Tax rate \(\times\) (Salvage value - Book value)
For Year 5:
Tax on salvage value\(= 0.30 \times ($10,000 - $0) = $3,000\)
For Year 4 (if scrapped):
Tax on salvage value\(= 0.30 \times ($15,000 - $10,000) = $1,500\)
Now, let's calculate the after-tax cash flows for each year:
Year 1:
After-tax cash flow = Depreciation expense per year - Tax on salvage value
After-tax cash flow = $10,000 - $0 = $10,000
Year 2:
After-tax cash flow = Salvage value - Tax on salvage value
After-tax cash flow = $0 - $0 = $0
Year 3:
After-tax cash flow = Salvage value - Tax on salvage value
After-tax cash flow = $0 - $0 = $0
Year 4 (if scrapped):
After-tax cash flow = Salvage value - Tax on salvage value
After-tax cash flow = $15,000 - $1,500 = $13,500
Year 5:
After-tax cash flow = Salvage value - Tax on salvage value
After-tax cash flow = $10,000 - $3,000 = $7,000
Now, let's calculate the net present value (NPV) using the cost of capital of 12%.
We will discount each year's after-tax cash flow to its present value using the formula:
\(PV = CF / (1 + r)^t\)
Where:
PV = Present value
CF = Cash flow
r = Discount rate (cost of capital)
t = Time period (year)
NPV = PV Year 1 + PV Year 2 + PV Year 3 + PV Year 4 + PV Year 5 - Initial investment
Let's calculate the NPV:
PV Year 1 \(= $10,000 / (1 + 0.12)^1 = $8,928.57\)
PV Year 2 \(= $0 / (1 + 0.12)^2 = $0\)
PV Year 3 \(= $0 / (1 + 0.12)^3 = $0\)
PV Year 4 \(= $13,500 / (1 + 0.12)^4 = $9,551.28\)
PV Year 5 \(= $7,000 / (1 + 0.12)^5 = $4,474.39\)
NPV = $8,928.57 + $0 + $0 + $9,551.28 + $4,474.39 - $50,000
NPV = $22,954.24 - $50,000
NPV = -$27,045.76
The NPV is negative, which means that based on the given assumptions and cost of capital, the investment in the new piece of equipment would result in a net loss.
Therefore, the investment may not be favorable.
Please note that the calculations above are based on the given assumptions, and additional factors or considerations specific to the business should also be taken into account when making investment decisions.
For similar questions on assumptions.
https://brainly.com/question/15424356
#SPJ8
The complete question may be like :
Assumptions: Tax depreciation is straight-line over five years. Pre-tax salvage value is $10,000 in Year 5 and $15,000 if the asset is scrapped in Year 4. Tax on salvage value is 30% of the difference between salvage value and book value of the investment. The cost of capital is 12%.
You are evaluating an investment in a new piece of equipment for your business. The initial investment cost is $50,000. The equipment is expected to have a useful life of five years.
Using the given assumptions, calculate the after-tax cash flows for each year and evaluate the investment decision by calculating the net present value (NPV) using the cost of capital of 12%.