Line g passes through points (1, 1) and (10,9). Line h is perpendicular to g. What is the
slope of line h?
Answers
Answer:
-9/8
Step-by-step explanation:
Slope m = (y2-y1)/(x2-x1)
using (1,1) and (10,9)
m = (9 - 1)/(10 - 1)
m = (8)/(9)
m = 8/9
slope of line g is 8/9
Perpendicular lines have slopes that are negative reciprocals of one another
so slope of h is -9/8
Related Questions
You invest $5,000 into a CD that is compounded every month. The interest rate is
1.25% and you leave the money in the CD for 5 years. How much money do you
have in your CD at the end of the 5 years?

Answers
You will have $5,333.85 in your CD at the end of the 5 years.
The formulation for the future value of an investment with monthly compounding is:
\(CD = P(1 + \frac{r}{n} )^{(nt)}\)
Wherein:
CD = final amountP = primary amountr = annual interest charge (as a decimal)n = number of times the interest is compounded in step with 12 monthst = time (in years)Plugging in the given values:
\(CD= 5000(1 + \frac{0.0125}{12} )^{(12*5)}\)
\(CD = 5000(1.00104)^{60}\)
CD = 5000(1.06677)
CD = $5,333.85
Consequently, you will have $5,333.85 in your CD at the end of the 5 years.
Learn more about Compound Interest Formula:-
https://brainly.com/question/28020457
#SPJ1
2-period production economy: Economy has two periods, = 0,1. There is a
representative household and a representative firm. Household utility is given as
U(Co,C1) = log(Co)+ß log(C1) where ß E (0,1) is a discount factor. Firm production
function is given as F(K,L) = K«L1-a, where a € (0,1) is a capital share. Household is
endowed with initial level of capital K o in period O and maximum labor hours L= 1 in
each period += 0,1. Firms rent capital and hire labor every period and maximize their
profit.
(a) Write down Household's problem
(b) Write down Firm's problem
(c) Write down market clearing conditions
(d) Write down Social Planner's Problem
(e) Define Competitive Equilibrium
(f) Solve Social Planner's Problem: Show your steps to solve it
(g) Solve Competitive Equilibrium: Show your steps to solve it(h) Write down First
Welfare Theorem. Does the theorem hold? Verify it.
(i) Write down Second Welfare Theorem. Does the theorem hold? Verify it.
Answers
The provided questions cover various aspects of a 2-period production economy, including the household's problem, firm's problem, market clearing conditions, Social Planner's Problem, competitive equilibrium, and welfare theorems.
(a) The Household's problem is to maximize its utility over two periods subject to its budget constraint. The household's problem can be formulated as follows:
Max U(Co, C1) = log(Co) + ß log(C1)
subject to the budget constraint:
Co + (1+r)C1 ≤ (1+r)Ko + W0 + W1,
where Co and C1 are consumption in period 0 and 1 respectively, ß is the discount factor, r is the interest rate, Ko is the initial capital endowment, W0 and W1 are the wages in periods 0 and 1 respectively.
(b) The Firm's problem is to maximize its profit by choosing the optimal combination of capital and labor. The firm's problem can be formulated as follows:
Maximize F(K, L) - RK - WL,
where F(K, L) is the production function, K is capital, L is labor, R is the rental rate of capital, and W is the wage rate.
(c) The market clearing conditions are:
Capital market clearing: K1 = (1 - δ)K0 + S - C0, where δ is the depreciation rate, S is savings, and C0 is consumption in period 0.
Labor market clearing: L = L0 + L1, where L0 and L1 are labor supplies in periods 0 and 1 respectively.
(d) The Social Planner's Problem is to maximize social welfare, which is the sum of the household's utility and the firm's profit. The Social Planner's Problem can be formulated as follows:
Maximize U(C0, C1) + F(K, L) - RK - WL,
subject to the production function F(K, L) and the market clearing conditions.
(e) A Competitive Equilibrium is a situation where all markets clear and agents (household and firm) make optimal decisions based on prices and market conditions. It is characterized by the following conditions:
Household's problem is solved optimally.
Firm's problem is solved optimally.
Market clearing conditions hold.
(f) To solve the Social Planner's Problem, we need to set up the Lagrangian and solve for the optimal values of consumption, capital, and labor. The Lagrangian can be written as:
L = U(C0, C1) + F(K, L) - RK - WL + λ1[(1+r)K0 + W0 + W1 - Co - (1+r)C1] + λ2[K1 - (1 - δ)K0 + S - C0] + λ3[L - L0 - L1],
where λ1, λ2, and λ3 are the Lagrange multipliers.
(g) To solve the Competitive Equilibrium, we need to determine the prices of capital (R) and labor (W) that clear the markets. This can be done by equating the demand and supply of capital and labor, and solving the resulting equations.
(h) The First Welfare Theorem states that under certain conditions, a competitive equilibrium is Pareto efficient. It implies that a competitive equilibrium is a socially optimal allocation of resources. To verify the theorem, we need to demonstrate that the competitive equilibrium allocation is Pareto efficient.
(i) The Second Welfare Theorem states that any Pareto efficient allocation can be achieved as a competitive equilibrium with appropriate redistribution of initial endowments.
To verify the theorem, we need to show that given an initial Pareto efficient allocation, we can find prices and redistribution of endowments that lead to a competitive equilibrium that achieves the same allocation.
For more such question on production. visit :
https://brainly.com/question/2292799
#SPJ8
What is the measure of an interior angle of a 21-gon?162.86°90°360°3420°
Answers
Question:
What is the measure of an interior angle of a 21-gon?
Concept:
Define a 21-gon
A 21-gon is a 21 sided polygon also know as An icosikaihenagon
In the case of this polygon, the value of n is
\(n=21\)We will then calculate the sum of interior angles of a 21-gon and then divide the sum by the number of sides n...
Therefore,
The formula we will use to calculate the measure of an interior angle of a 21-gon is given below as
\(\begin{gathered} \text{meausre of an interior angle=}\frac{\text{sum of interior angles}}{\text{total number of sides}} \\ \end{gathered}\)The formula for the sum of interior angles is given below as
\(\text{sum of interior angle=(n}-2)\times180\)Hence,
We will have
\(\begin{gathered} \text{meausre of an interior angle=}\frac{\text{sum of interior angles}}{\text{total number of sides}} \\ \text{meausre of an interior angle}=\frac{(n-2)\times180^0}{n} \end{gathered}\)Step 2:
Substitute the value of n=21 in the formula above, we will have
\(\begin{gathered} \text{measure of an interior angle}=\frac{(n-2)\times180^0}{n} \\ \text{measure of an interior angle}=\frac{(21-2)\times180^0}{21} \\ \text{measureof an interior angle}=\frac{19\times180^0}{21} \\ \text{measure of an interior angle}=\frac{19\times180^0}{21} \\ \text{measure of an interior angle}=\frac{3420^0}{21} \\ \text{measure of an interior angle}=162.86^0 \end{gathered}\)Hence,
The final answer = 162.86°
help pleaseeeeeeeeee

Answers
Which angle has a measure equal to the sum of the m∠SQR and the m∠QRS? ∠RSC ∠SRE ∠DQS ∠QSR
Answers
angle has a measure equal to the sum of the the question is ∠DQS.
According to the problem, we need to find an angle whose measure is equal to the sum of the measures of ∠SQR and ∠QRS. We can use the angle addition postulate which states that the measure of an angle formed by two adjacent angles is equal to the sum of their measures.
Let's consider angle ∠DQS. This angle is formed by adjacent angles ∠SQR and ∠QRS. Therefore, according to the angle addition postulate, the measure of angle ∠DQS is equal to the sum of the measures of ∠SQR and ∠QRS.
Thus, we can conclude that the angle ∠DQS has a measure equal to the sum of the measures of ∠SQR and ∠QRS.
To know more about angle visit:
https://brainly.com/question/31818999
#SPJ11
Can someone help me? With all the problems and with work

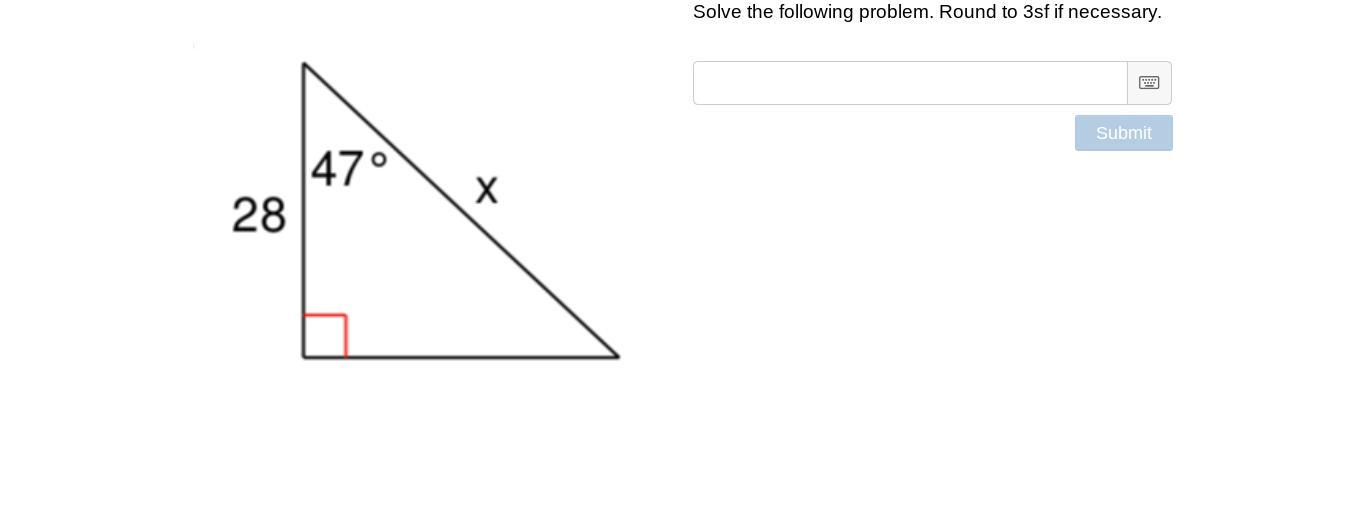



Answers
Answer:
5.006
41.056
31.289
51.977
7.884
Step-by-step explanation:
1) sin x = opposite side / hypotenuse
sin 24.3° = 2.06 / hyp
hyp = 2.06 / sin 24.3 = 5.0059006616019108320511866543651
rounding to 3 significant figures
= 5.006
2)cos x = adjacent side / hypotenuse
cos 47 = 28 / x
x = 28 / cos 47 = 41.055817197909497891901840157945
= 41.056
3) cos x = adjacent side / hypotenuse
cos 56.1 = x / 56.1
x = 56.1 * cos 56.1 = 31.289500613760617368691451544764
= 31.289
4) tan x = opposite side / adjacent side
tan 68 = x / 21
x = 21 * tan 68 = 51.9768239217422123300402781676
= 51.977
5) sin x = opposite side / hypotenuse
sin 21 = x / 22
x = 22 * sin 21 = 7.8840948899966060166510313670963
= 7.884
3-y/2 =1. Help please
Answers
-3 -3
-y/2=-2
x2 x2
-y=-4
/-1 /-1
Y=4
100 points and a Brainliest
just answer this question
what is dabi real name off of my hero academia
Answers
Answer: Toya Todoroki
Step-by-step explanation:
Answer:
Touya Todoroki
Step-by-step explanation:
i used to watch the show
HELP WILL MAKE BRAINLIEST
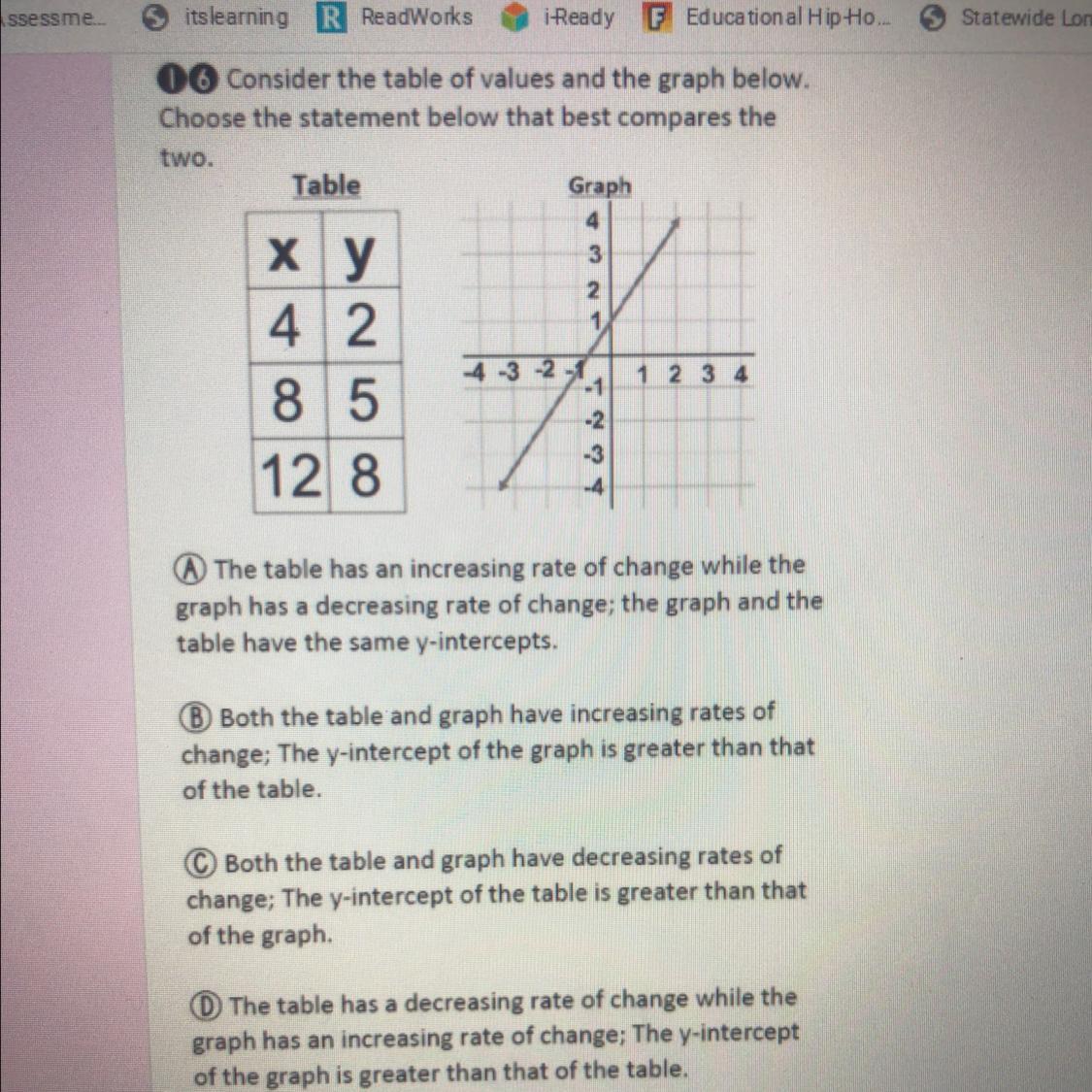
Answers
Answer:
x
Step-by-step explanation:
Write a linear function (y=mx+b) or an exponential function (y=a(b)x) that models the data.

Answers
To model the given data points, we can use a linear function of the form y = mx + b.
First, we need to find the slope (m) of the line:
m = (y2 - y1) / (x2 - x1)
m = (-6 - (-2)) / (1 - 0)
m = -4/1
m = -4
Now, we can use the slope and one of the points to find the y-intercept (b):
y = mx + b
-2 = (-4)(0) + b
b = -2
Therefore, the linear function that models the given data is:
y = -4x - 2
a dressmaker needs to cut 12-inch pieces of ribbon from rolls of ribbon that are 3 feet in length. how many 12-inch pieces can the dressmaker cut from 10 of these rolls of ribbon?
Answers
The dressmaker can cut 30 pieces of 12-inch long ribbon from 10 of these rolls of ribbon.
A dressmaker needs to cut 12-inch pieces of ribbon from rolls of ribbon that are 3 feet in length.
We are to determine how many 12-inch pieces the dressmaker can cut from 10 of these rolls of ribbon.
To do this, we need to find out the number of 12-inch pieces in 3 feet of ribbon and multiply that number by 10 (since we have 10 rolls of ribbon).
Let's begin by converting 3 feet into inches as follows;1 foot = 12 inches
Therefore,
3 feet = 3 × 12 inches
= 36 inches
From the above, we know that the dressmaker has 36 inches of ribbon to cut into 12-inch pieces.
Thus, the number of 12-inch pieces that can be cut from 36 inches of ribbon is given by dividing 36 by 12 as follows;
Number of 12-inch pieces = 36 ÷ 12
= 3 pieces
Therefore, from one roll of ribbon, the dressmaker can cut 3 pieces of 12-inch long ribbon
From 10 rolls of ribbon, the number of 12-inch pieces that can be cut is 10 × 3 = 30 pieces.
Hence, the dressmaker can cut 30 pieces of 12-inch long ribbon from 10 of these rolls of ribbon.
Know more about inches here:
https://brainly.com/question/876758
#SPJ11
What are the slope and y-intercept of 25x - 20y = 100
Answers
What are the slope and y-intercept of
25x - 20y = 100
-20y = 100 - 25x
20y = 25x - 100 (dividing by 20)
y= (25/20)x - 5
y= (5/4)x - 5
So, the slope is 5/4 and the y-intercept is 5.
6 38/45 + 2 5/9
Enter your answer in the box as a mixed number in simplest form.
Answers
Answer:
9 2/5
Step-by-step explanation:
6 38/45 + 2 5/9
6 38/45 + 2 25/45 = 8 63/45 = 9 18/45 = 9 2/5
what is the mode of 250 100 75 200 150 100?
Answers
\(\textbf{Heya !}\)
the mode is the number that occurs the most
All numbers here occur once, except \(\sf{100}\).
so 100 is the mode.
`hope it was helpful to u ~
The Precision Scientific Instrument Company manufactures thermometers that are supposed to give readings of o°C at the freezing point of water. Tests on a large sample of these thermometers reveal that at the freezing point of water, some give readings below O°C (denoted by negative numbers) and some give readings above O C (denoted by positive numbers). Assume that the mean reading is 0°C and the standard deviation of the readings is 1.00°C. Also assume that the frequency distribution of errors closely resembles the normal distribution. A thermometer is randomly selected and tested. A quality control analyst wants to examine thermometers that give readings in the bottom 4%. Find the temperature reading that separates the bottom 4% from the others. Round to two decimal places. A. -1.48B.-1.89 C. -1.63 D. -1.75
Answers
Solution :
It is given that the Precision Scientific Instrument company Manufactures thermometers that provide readings at 0 degree Celsius for the freezing point of water.
A quality control analyst examines the thermometers which provide readings in the bottom of 4%.
Using the standard normal table, we get
P(z < z) = 4%
P(z < z) = 0.04
See the probability of 0.04 in the standard normal corresponding to the z-value is = -1.75
Therefore,
P(z < -1.75) = 0.04
z = -1.75
So the temperature reading that separates the bottom of 4% from the other thermometers is - 1.75°C
Therefore correct option is (D). -1.75
Problem-solving Helen shares £360 between her three children, Felix, George and Harry.
Felix receives 30% of the money.
The ratio George and Harry receive is 4 : 5.
Work out how much George receives
Answers
George receives £112 based on the given data regarding the 4:5 ratio.
Felix receives 30% of £360 which is:
30/100 x £360 = £108The total amount remaining for George and Harry is:
£360 - £108 = £252The ratio of the amount that the George receives to the amount that the Harry receives is 4:5. This means that the total ratio of the amount they receive is:
4+5 = 9
To find out how much George receives, we need to divide the total of the amount by the total of the ratio and then multiply by George's share of the ratio:
£252 ÷ 9 x 4 = £112
Therefore, George receives £112.
Learn more about the ratio
https://brainly.com/question/2328454
#SPJ4
What is the length of the shorter leg?
What is the length of the longer leg?

Answers
Using Pythagoras theorem to set a system of equations, the longer side is 11 unit and shorter side is 3 unit
System of EquationA system of equations is a set of two or more equations containing two or more variables. The goal of a system of equations is to find the values of the variables that satisfy all of the equations simultaneously.
In this problem, we can define our unknown variables as;
Let;
x = shorter legy = longer legUsing Pythagoras theorem;
x² + y² = (√130)²
x² + y² = 130 ...(i)
The perimeter of the triangle is the sum of sides in the triangle.
x + y + √130 = 14 + √130
x + y = 14 + √130 - √130
x + y = 14 ...eq(ii)
From equ(ii)
x = 14 - y ...eq(iii)
Put eq(iii) into eq(i)
x² + y² = 130
(14 - y)² + y² = 130
y² - 28y + 196 + y² = 130
2y² - 28y + 66 = 0
Solving the quadratic equation
y = 11
Put y = 11 into equ(ii)
x + y = 14
x + 11 = 14
x = 3
The shorter side is 3 units and longer side is 11 units
Learn more on system of equation here;
https://brainly.com/question/13729904
#SPJ1
Justin drove 804 miles in 12 hours.
At the same rate, how many miles would he drive in 5 hours?
Answers
Answer:
335 Miles
Step-by-step explanation:
804/12 = 67 MPH
5 × 67 = 335
What is the length of the unlabled side of the triangle?

Answers
Answer:
a or b (probably a)
Step-by-step explanation:
Compute each of the following Galois groups. Which of these field extensions are normal field extensions? If the extension is not normal, find a normal extension of Q in which the extension field is contained
Answers
To compute the Galois groups and determine if the field extensions are normal, we need to know the specific field extensions in question. However, I will provide a general method for computing Galois groups and determining normal field extensions.
Step 1: Identify the field extension
Let's say our field extension is given by K/Q, where K is the extension field and Q is the base field (the field of rational numbers).
Step 2: Determine the minimal polynomial
Find the minimal polynomial f(x) of the field extension K/Q. This is the smallest degree polynomial with rational coefficients for which the elements of K are roots.
Step 3: Compute the Galois group
The Galois group, G(K/Q), is the group of automorphisms of the field K that fix the base field Q. To compute G(K/Q), determine the set of automorphisms of K that keep the elements of Q fixed.
Step 4: Check for normality
A field extension K/Q is normal if and only if the minimal polynomial f(x) splits into distinct linear factors over K. If this is true, then K/Q is a normal field extension.
Step 5: Find a normal extension if necessary
If K/Q is not normal, we can find a normal extension L/Q containing K by considering the splitting field of the minimal polynomial f(x) over Q. The splitting field L is the smallest field containing Q and all the roots of f(x), and the extension L/Q will be normal.
for such more questions on minimal polynomial
https://brainly.com/question/23827775
#SPJ11
dairy queen is a take-out yogurt shop owned by linda smith. customers arrive at a rate of 25 per hour. linda serves a customer, on the average, in 1.5 minutes. assume that the arrivals and the service times are poisson distributed and exponentially distributed, respectively. what is the probability that a customer will wait in a line between 3 to 6 minutes?
Answers
The probability that a customer will wait in a line between 3 to 6 minutes is about 16.58%.
To solve this problem, we need to use the Poisson process and the exponential distribution.
Let X be the number of arrivals in a 3-minute interval. Since customers arrive at a rate of 25 per hour, the expected number of arrivals in a 3-minute interval is:
λ = (25/60) x 3 = 1.25
Thus, X is Poisson distributed with parameter λ = 1.25.
Let Y be the service time for a customer. Since Linda serves a customer, on average, in 1.5 minutes, Y is exponentially distributed with parameter μ = 1/1.5 = 0.6667.
Let Z be the waiting time for a customer in the line. Z is the sum of X independent service times, so Z is gamma distributed with parameters X and μ.
We want to find the probability that Z is between 3 and 6 minutes:
P(3 ≤ Z ≤ 6) = ∫∫ f(x,y) dx dy
where f(x,y) is the joint probability density function of X and Y:
f(x,y) = (λ^x / x!) e^(-λ) μ e^(-μy) = (1.25^x / x!) e^(-1.9167) e^(-0.6667y)
Now we can evaluate the double integral:
P(3 ≤ Z ≤ 6) = ∫∫ f(x,y) dx dy
= ∫∫ (1.25^x / x!) e^(-1.9167) e^(-0.6667y) dx dy
= ∫ e^(-0.6667y) e^(-1.9167) ∑ (1.25^x / x!) dx dy (x=0 to ∞)
= e^(-1.9167) ∫ e^(-0.6667y) e^(1.25) dy ∑ (1.25^x / x!) (x=0 to ∞)
The sum in the integral is the Taylor series expansion of e^1.25, which is equal to e^1.25 = 3.4903.
Using a table of integrals or a computer software, we can evaluate the integral:
∫ e^(-0.6667y) e^(1.25) dy = (1/0.6667) (e^(1.25) - e^(-0.6667(6))) = 3.7225
Therefore, the probability that a customer will wait in a line between 3 to 6 minutes is:
P(3 ≤ Z ≤ 6) = e^(-1.9167) ∫ e^(-0.6667y) e^(1.25) dy ∑ (1.25^x / x!) (x=0 to ∞)
= e^(-1.9167) (3.7225) (3.4903) = 0.1658 or about 16.58% (rounded to four decimal places).
Therefore, the probability that a customer will wait in a line between 3 to 6 minutes is about 16.58%.
Learn more about probability here:
https://brainly.com/question/30034780
#SPJ11
Letf(x, y) = 2ex − y.Find the equation for the tangent plane to the graph of f at the point
Answers
The final equation for the tangent plane to the graph of f at the point (a, b) is z = 2e^a(x - a) - y + 2e^a - 2b. This equation represents the plane that is tangent to the graph of f at the specified point (a, b).
To find the equation for the tangent plane to the graph of the function f(x, y) = 2e^x - y at a given point (x0, y0), we need to calculate the partial derivatives of f with respect to x and y at that point.
The partial derivative of f with respect to x, denoted as ∂f/∂x or fₓ, represents the rate of change of f with respect to x while keeping y constant. Similarly, the partial derivative of f with respect to y, denoted as ∂f/∂y or fᵧ, represents the rate of change of f with respect to y while keeping x constant.
Let's calculate these partial derivatives:
fₓ = d/dx(2e^x - y) = 2e^x
fᵧ = d/dy(2e^x - y) = -1
Now, we have the partial derivatives evaluated at the point (x0, y0). Let's assume our point of interest is (a, b), where a = x0 and b = y0.
At the point (a, b), the equation for the tangent plane is given by:
z - f(a, b) = fₓ(a, b)(x - a) + fᵧ(a, b)(y - b)
Substituting fₓ(a, b) = 2e^a and fᵧ(a, b) = -1, we have:
z - f(a, b) = 2e^a(x - a) - (y - b)
Now, let's substitute f(a, b) = 2e^a - b:
z - (2e^a - b) = 2e^a(x - a) - (y - b)
Rearranging and simplifying:
z = 2e^a(x - a) - (y - b) + 2e^a - b
The final equation for the tangent plane to the graph of f at the point (a, b) is z = 2e^a(x - a) - y + 2e^a - 2b.
This equation represents the plane that is tangent to the graph of f at the specified point (a, b).
Learn more about tangent here:
https://brainly.com/question/10053881
#SPJ11
the world population in 1997 was 5.88billion. the world population in 2017was 7.53billion. assume that the ratio between the population in two consecutive years was constant between 1997 and 2017. which equation can be used to find r,the rate of growth per year of the world population?
Answers
The equation that can be used to find r, the rate of growth per year of the world population, is \(r = (7.53 / 5.88 )^{(1/20)} - 1\).
If we assume that the growth rate of the world population was constant from 1997 to 2017, then we can use the following equation:
Population in 2017 = Population in 1997 × (1 + r)²⁰
where r is the annual growth rate, and the exponent 20 represents the number of years between 1997 and 2017.
We can rewrite this equation to solve for r:
(7.53 ) = (5.88 ) × (1 + r)²⁰
Divide both sides by (5.88 ):
(7.53 ) / (5.88 ) = (1 + r)²⁰
Take the 20th root of both sides:
\((7.53 / 5.88 )^{(1/20)} = 1 + r\)
Subtract 1 from both sides:
\(r = (7.53 / 5.88 )^{(1/20)} - 1\)
Therefore, the equation that can be used to find r, the rate of growth per year of the world population, is \(r = (7.53 / 5.88 )^{(1/20)} - 1\).
Learn more about the growth rate here:
https://brainly.com/question/29291084
#SPJ1
LetXbe a random variable that has a population mean ofμand a variance ofσ2; that isE(X)=μ;Var(X)=σ2. Answer the following using the definitions and properties of expected value and variance that were discussed in Lecture 4. (a) Starting with the expressionVar(X)=E[(X−μ)2], show that the variance can also be written asVar(X)=E(X2)−μ2. (b) Write an expression for a random variableZthat is constructed by standardizingX:Z=(c) Show thatE(Z)=0(d) Show thatVar(Z)=1(e) Show that the sample meanXˉof a random sample of sizendrawn from the population is an unbiased estimator for the population meanμ. Start by writing down the condition for unbiasedness.
Answers
(a) Starting with the expression Var(X)=E[(X−μ)2], we can rearrange to get E[(X−μ)2] = Var(X)+μ2. Therefore, Var(X)=E(X2)−μ2.
(b) A random variable Z that is constructed by standardizing X is written as Z = (X-μ)/σ.
(c) E(Z) = E[(X-μ)/σ] = (E[X] - μ)/σ = 0.
(d) Var(Z) = Var[(X-μ)/σ] = (Var[X] - μ2)/σ2 = 1.
(e) The sample mean of a random sample of size n drawn from the population is an unbiased estimator for the population mean μ if E[sample mean] = μ.
For more such questions on Var(X).
https://brainly.com/question/30896955#
#SPJ11
a^2+3a=7 Discriminant = _______________ Number of solutions for the quadratic equation = ________
Answers
Answer:
2 distinct solutions
Step-by-step explanation:
discriminant is b²-4ac
b = 3
a = 1
c = -7
discriminant = 9-4(-7) = 9+28 = 37
mention about angles of a triangle
Answers
inches
2 yards 2 inches =
Answers
Answer:
74 inches
Step-by-step explanation:
1 yard = 36 inches
then 2 yards = 72
and 72 + 2 inches = 74 inches
A shoe store uses a markup rate 40% when determining the retail price of its items. If the store pays $42.25 for a pair of shoes wholesale, what will be the retail price of that pair of shoes?
Answers
42.25 x .4 = 16.90
42.25 + 16.90 = 59.15
An item is priced at $13.46. If the sales tax is 6%, what does the item cost including sales tax?
Answers
.80 + 13.46 =14.46.
Answer: $14.46
Oliver made 5% of his free throws over the season. If he shot 120 free throws, how many did he make?
Answers
Answer:
6 free throws
Step-by-step explanation:
you do 120 divided by 0.05 (which is 5 percent in decimal form) and get 6.