lim of x goes to a x minus a divided by the square root of x minus square root of a
A. negative 2 times the square root of a
B. 2 times the square root of a
C. the square root of a
D. 2a
Answers
Answer:
i know a nice song it's called hi guy. you are cool and smart
Step-by-step explanation:
you should take a bath everyday
Related Questions
help pls!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Answers
Answer:
y = -3x - 1
hope this helps!
The point P=(1/2,y)lies on the unit circle shown below. What is the value of y in simplest form?
Answers
The value of y in simplest form for the point P = (1/2, y) lying on the unit circle is y = ± √(3)/2.
To find the value of y in simplest form for the point P = (1/2, y) lying on the unit circle, we can use the equation of the unit circle, which states that for any point (x, y) on the unit circle, the following equation holds: x^2 + y^2 = 1.
Plugging in the coordinates of the point P = (1/2, y), we get:
(1/2)^2 + y^2 = 1
1/4 + y^2 = 1
y^2 = 1 - 1/4
y^2 = 3/4.
To simplify y^2 = 3/4, we take the square root of both sides:y = ± √(3/4).
Now, we need to simplify √(3/4). Since 3 and 4 share a common factor of 1, we can simplify further: y = ± √(3/4) = ± √(3)/√(4) = ± √(3)/2.
for more search question point
https://brainly.com/question/28162977
#SPJ8
x=.9875 and y =.675 what is w
Answers
Since w = x + y + missing part
Since x = 0.9875 and y = 0.675, then
\(\begin{gathered} w=0.9875+0.6750+\text{missing part} \\ w=1.6625+\text{missing part} \end{gathered}\)You should add 0 to 0.675 to be 0.6750 because the other number has 4 decimal places to do the addition correctly
Since we do not know the value of the missing part, but we know that it will add to 1.6625, so the answer must be greater than 1.6625
X to the third power equals 512
Answers
Answer:
8
Step-by-step explanation:
Point slope form & slope intercept form

Answers
The equation is in the slope form & the slope-intercept form will be y=-32/3x+4
What is a straight line?A straight line is a combination of endless points joined on both sides of the point.
The slope 'm' of any straight line is given by:
A linear equation has the form y = mx + b in the slope-intercept format. X and Y are the variables in the equation. The values m and b represent the line's slope (m) and the value of y when x is 0.
\(\rm m =\dfrac{y_2-y_1}{x_2-x_1}\)
It is given that, the x-intercept is -3/8 and the y-intercept is 4. The equation of the line is,
The slope of the line is,
\(\rm m =\dfrac{y_2-y_1}{x_2-x_1} \\\ m = \frac{4}{\frac{-3}{8} } \\\ m=\frac{-32}{3}\)
The equation of the line is,
y=mx+c
y=-32/3x+4
Thus, the equation is in the slope form & the slope-intercept form will be y=-32/3x+4
Learn more about the straight line here:
brainly.com/question/3493733
#SPJ1
Translate 2 3 y − 9 < y + 1 into a sentence. Nine than two-thirds of number is less than the number .
Answers
The sentence translation of "2/3y - 9 < y + 1" is "Nine less than two-thirds of a number is less than the number."
To translate the inequality expression "2/3y - 9 < y + 1" into a sentence, we can break it down into smaller parts:
"2/3y" represents two-thirds of a number.
"9" represents the number nine.
"y + 1" represents the number increased by one.
Now let's construct the sentence:
"Nine less than two-thirds of a number" - This refers to the expression "2/3y - 9," indicating that we have subtracted nine from two-thirds of a number.
"is less than" - This is the comparison symbol in the inequality.
"the number" - This refers to the expression "y + 1," representing the number increased by one.
Combining these parts, we form the sentence: "Nine less than two-thirds of a number is less than the number."
Hence, the correct sentence translation of "2/3y - 9 < y + 1" is "Nine less than two-thirds of a number is less than the number."
For more such questions on sentence translation, click on:
https://brainly.com/question/28958546
#SPJ8
The measure of the angle is 17 times greater than its supplement.
Answers
Answer: supplement <17
Step-by-step explanation:
1. 17 is greater
2. supplement is smaller
A researcher is exploring the notion that there is an economy of scale in raising children. While having one child might add to a family's financial stress, the second or third one might not be as "expensive" since they would already be sharing one roof, could share clothing, etc. The researcher has access to a large community of parents where 15% have one child under 18 in their home, 65% of parents have two children, and 20% of parents have three or more children. Rounded to the nearest whole number, the probability that any given family who is selected has two or more children at home is ________ %?
Answers
Answer:
The probability is \(G = 85% \)
Step-by-step explanation:
From the question we are told that
The percentage of parents that have one child under 18 in their homes is k = 15%
The percentage of parents that have two children is T = 65%
The percentage of parents that have three or more children is Y = 20%
Generally the probability that any given family who is selected have two or more children at home is mathematically evaluated as
\(G = T + Y\)
=> \(G = 65% + 20% \)
=> \(G = 85% \)
what does the line "wants him to be a doctor" reveal about Papi's view of his son in sol painting, inc.?
Answers
if the distance between the points (5, 2) and (9, a) is 25 units then find the value of a?
Answers
Answer:
15 just the answer because of the value given above
Answer: Value of A is 5.
Step-by-step explanation:what expressions are equivalent to 16a+72
Answers
The expressions which are equivalent to 16a + 72 are 2(8a + 36) and 4(4a + 18)
Expressions16a + 72
Factorise= 4(4a + 18)
Also
16a + 72
factorise= 2(8a + 36)
The equivalent expressions to 16a + 72 are 2(8a + 36) and 4(4a + 18)
Learn more about expressions:
https://brainly.com/question/723406
#SPJ1
Find the average value of f(x)=−2sin(x)+5cos(x) over the interval [π,2π] .
Answers
The average value of the trigonometric equation f(x) = - 2 · sin x + 5 · cos x over the interval [π, 2π] is equal to 2 / π.
How to determine the average value of a function on a given intervalIn this question we find the definition of a trigonometric equation consisting in the sum of two trigonometric functions on a given interval [a, b], of which we must determine its average value by means of the following integral equation:
\(m = \frac{1}{b - a} \cdot \int\limits^b_a {f(x)} \, dx\)
Where:
a - Lower boundb - Upper boundFirst, write the entire trigonometric equation and the bounds of the interval:
f(x) = - 2 · sin x + 5 · cos x, a = π, b = 2π
Second, obtain the result of the integral equation:
\(m = -\frac{2}{2\pi - \pi}\cdot \int\limits^{2\pi}_\pi {\sin x} \, dx + \frac{5}{2\pi - \pi}\cdot \int\limits^{2\pi}_\pi {\cos x} \, dx\)
\(m = \frac{2}{\pi}\cdot \cos x\) \(|\limits_{\pi}^{2\pi}\) + \(\frac{5}{\pi}\cdot \sin x\) \(|\limits_{\pi}^{2\pi}\)
m = (2 / π) · (cos 2π - cos π) + (5 / π) · (sin 2π - sin π)
m = (2 / π) · (1 - (- 1)) + (5 / π) · (0 - 0)
m = 2 / π
To learn more on average values on functions: https://brainly.com/question/22847740
#SPJ1
![Find the average value of f(x)=2sin(x)+5cos(x) over the interval [,2] .](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/HKBTPAh9mXlTJXbDFsHP4qhlOzbgpbQR.png)
The relationship between pressure (P),
volume (V), and temperature (T) for
an ideal gas is stated by the Ideal Gas
Law: PV = nRT, where n is the number
of moles and R is the universal gas
constant. If n is kept constant, which of
these statements is not true according to
the equation?
A Decreased volume at constant
pressure reduces temperature.
B Decreased volume at constant
temperature increases pressure.
C Decreased temperature at constant
volume reduces pressure.
D Decreased temperature at constant
volume increases pressure.
Answers
Answer:
A
Step-by-step explanation:
For an ideal gas : PV=RT
And the internal energy of an ideal gas:
E
in
=
2
3
RT
E
in
=
2
3
PV
V
E
in
=
2
3
P
Energy density (E)=
2
3
P
P=2/3E
Community gym $50 joining fee plus $55 per month Ultra Sports gym $20 joining fee plus $60 per month. write an equation that can be used to determine after how many months the fees for the two gyms will be the same. Be sure to define your variable 
Answers
Therefore , the solution of the given problem of equation comes out to be the two gyms' combined fees will be identical after six months of membership.
What is equation?Complex algorithms frequently employ variable words to demonstrate coherence between two opposing assertions. Equations are academic expressions that are used to demonstrate the equality of different academic figures. In this instance, normalization results in b + 7 rather than a singular formula that divides 12 through two parts as well as may be employed to evaluate data obtained from y + 7.
Here,
Assume that x is the total number of months that each gym's registration is valid.
The overall cost for Community Gym after x months can be calculated as follows:
=> C(x) = 50 + 55x
After x months, the overall expense for Ultra Sports Gym can be determined as follows:
=> U(x) = 20 + 60x
The number of months x for which the combined expenses for the two gyms are equal is what we're looking for. In order to find x, we can make the two equations equal to one another as follows:
=> C(x) = U(x)
=> 50 + 55x = 20 + 60x
After finding x, we obtain:
=> 5x = 30
=> x = 6
As a result, the two gyms' combined fees will be identical after six months of membership.
To know more about equation visit:
https://brainly.com/question/649785
#SPJ1
What is .7899 rounded 4 decimal places
Answers
Hope this helped. :)
Determine the amplitude of function

Answers
The amplitudes of functions are a) 8 and b) 6.
Given are the functions we need to determine the amplitude of function,
a) y = 8 Sin (x/2) + 3
b) y = 6 Cos x + 2
So,
To determine the amplitude of a trigonometric function, you can follow these steps:
For a sine function of the form y = A×sin(Bx + C) + D:
The amplitude is equal to the absolute value of the coefficient A.
For a cosine function of the form y = A×cos(Bx + C) + D:
The amplitude is equal to the absolute value of the coefficient A.
Let's apply these steps to the given functions:
a) y = 8×sin(x/2) + 3
The coefficient of sin in this function is 8, so the amplitude is |8| = 8.
Therefore, the amplitude of function a) is 8.
b) y = 6×cos(x) + 2
The coefficient of cos in this function is 6, so the amplitude is |6| = 6.
Therefore, the amplitude of function b) is 6.
Hence the amplitudes of functions are a) 8 and b) 6.
Learn more about amplitude click;
https://brainly.com/question/9525052
#SPJ1
M is between C and G. If CM = x , MG = x +12, and CG= 4x +6.
с
M
Answers
Answer:
CM = 3
MG = 15
CG = 18
Step-by-step explanation:
CM = x
MG = x + 12
C to G equals 4x + 6
CG = 4x + 6
And CM + MG (CG) also equals 2x + 12
CM + MG = 2x + 12
4x + 6 = 2x + 12 (solve for x)
Subtract 2x from both sides.
2x + 6 = 12
Subtract 6 from both sides.
2x = 6
Divide by 2
x = 3
CM = (3)
MG = 3 + 12 = 15
CG = 4(3) + 6 = 18
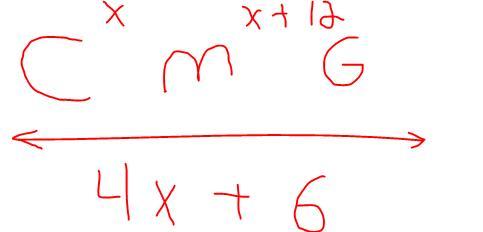
At a school camp there is enough foot for 150 students for 5 days.
Q: How long would the food last if there were only 100 students?
Answers
Answer:
Step-by-step explanation:
you need to find how much food is used for 1 person then times that answer by 100 to find how much food is needed
Maine has a cold climate in the winter. What is the probability of the temperature falling below 32 Fahrenheit in Maine during the month of January.
Answers
The probability is closer to one than zero.
Probability theory is used to analyze and predict the likelihood of events happening in various fields such as statistics, gambling, physics, finance, and more. It allows us to make informed decisions based on the likelihood of different outcomes. In probability theory, the total number of possible outcomes is important to determine the probability of a single event occurring. By comparing the favorable outcomes to the total outcomes, we can calculate the probability of an event happening.
Probability is a measure of the likelihood of an event to occur. Many events cannot be predicted with total certainty. We can predict only the chance of an event to occur i.e., how likely they are going to happen, using it. Probability can range from 0 to 1, where 0 means the event to be an impossible one and 1 indicates a certain event. Probability for Class 10 is an important topic for the students which explains all the basic concepts of this topic. The probability of all the events in a sample space adds up to 1.For example, when we toss a coin, either we get Head OR Tail, only two possible outcomes are possible (H, T). But when two coins are tossed then there will be four possible outcomes, i.e {(H, H), (H, T), (T, H), (T, T)}.
To know more about probability
brainly.com/question/17011124
It took Alfonzo 25 minutes to shop for a shirt. If he left the store at 2:25 P.M. after buying the shirt, what time did he start shopping?
Answers
The time he start shopping is 2 : 00 PM
How to determine the time he start shopping?From the question, we have the following parameters that can be used in our computation:
Time spent = 25 minutes
Time he left the store = 2 : 25PM
Using the above as a guide, we have the following:
Time he started = Time he left the store - Time spent
substitute the known values in the above equation, so, we have the following representation
Time he started = 2 : 25PM - 25 minutes
Evaluate
Time he started = 2 : 00 PM
Hence, the time he start shopping is 2 : 00 PM
Read more about expression at
https://brainly.com/question/15775046
#SPJ1
Given right triangle ABC with altitude CE. By the Right Triangle Altitude Theorem, which similarity statement is true?
△ABC ∼ △EBC
△ABC ∼ △AEC
△ABC ∼ △CBE
△ABC ∼ △BCE
(40 points)
Answers
Step-by-step explanation:
By the Right Triangle Altitude Theorem, the two triangles formed by the altitude of a right triangle are similar to the original triangle and to each other.
In this case, triangle ABC is the original right triangle and CE is the altitude. Therefore, the similarity statement that is true is:
△ABC ∼ △AEC
This is because triangles ABC and AEC are both right triangles that share the angle at C, and the altitude CE creates two pairs of congruent angles (the right angles and the angle at A and E) and a pair of proportional sides (CE and AE are corresponding altitudes).
So, we can write the similarity statement as:
△ABC ~ △AEC
What is the value of u?

Answers
Answer:
66-26 = 40
Step-by-step explanation:
u = 40 degrees
please help :( i don’t understand!
An engineer estimated the weight of a steel beam to be 150 pounds. The actual weight of the beam was 143 pounds.
Find the absolute error and the percent error of the engineer's estimate. If necessary, round your answers to the nearest tenth.
absolute error = ? (pounds)
percent error = ? (%)
Answers
Answer:
absolute error: 7 pounds
percent error:4.9%
Step-by-step explanation:
Absolute error:
150-143=7 pounds
Percent error:
=l\(\frac{150-143}{143}\) l x 100
=l\(\frac{7}{143}\)l x 100
=0.04895x100
=4.895...
=4.9%
find sum of arithmetic series where a1 = 7, n=31, an=127
Answers
2077
Explanation
To find the sum of an arithmetic sequence, use the formula
\(\begin{gathered} S_n=n(\frac{a_1+a_n}{2}) \\ \text{where} \\ n=the\text{ number of terms being added} \\ a_1=the\text{ firs term} \\ a_n=the\text{ nth term}(\text{ last term)} \end{gathered}\)Step 1
Let
\(\begin{gathered} a_1=7 \\ n=31 \\ a_n=127 \end{gathered}\)now, replace and calculate
\(\begin{gathered} S_n=n(\frac{a_1+a_n}{2}) \\ S_n=31(\frac{7+127}{2}) \\ S_n=31(\frac{134}{2}) \\ S_n=31(67) \\ S_n=2077 \end{gathered}\)therefore, the answer is
2077
I hope this helps you
Find a formula for the general term an of the sequence, assuming that the pattern of the first few terms continues. (Assume that n begins with 1.) −3, 2, − 4 3 , 8 9 , − 16 27 , ...
Answers
Answer:
The general term is
Sn = -(-2)ⁿ.3¹⁻ⁿ
step by step Explanation:
we were told to find a general term of the above sequence, what should come to mind is that the terms will follow an order....
CHECK THE ATTACHMENT FOR DETAILED EXPLANATION


The depth of a local lake averages 38 ft, which is represented as |−38|. In February, it measured 6 ft deep, or |−6|, and in July, it was 25 ft deep, or |−25|. What is the difference between the depths in February and July?
A32 feet
B 31 feet
C 19 feet
D 13 feet
Answers
The difference between the depths in February and July is 31 feet.
How to measure depth?The method of measuring depth depends on what we are trying to measure the depth of. Here are some general methods for measuring different types of depth:
Depth of water: The depth of water can be measured using a sounding device such as a sonar or a simple depth gauge. A sonar uses sound waves to determine the distance from the water's surface to the bottom. A depth gauge is a simple device that measures the distance from the surface of the water to the bottom using a weight and a line.
Depth of a hole: The depth of a hole can be measured using a tape measure or a ruler. Simply insert the measuring device into the hole and measure the distance from the top of the hole to the bottom.
Depth of a trench: The depth of a trench can be measured using a measuring tape or a surveyor's level. Place the measuring device at the edge of the trench and measure the distance from the top of the trench to the bottom.
Depth of a pool: The depth of a pool can be measured using a pool depth marker or by using a measuring tape. A depth marker is usually located on the side of the pool and indicates the depth at various points. Alternatively, you can use a measuring tape to measure the distance from the surface of the water to the bottom of the pool.
Depth of a well: The depth of a well can be measured using a well sounder or a tape measure. A well sounder is a device that sends a signal down the well and measures the time it takes for the signal to bounce back. The time it takes is then used to calculate the depth of the well. Alternatively, a tape measure can be used to measure the distance from the surface of the water to the bottom.
Given, In February, it measured 6 ft deep, or |−6| and in July, it was 25 ft deep, or |−25|.
The difference between the depths in February and July is:
|−6| − |−25| = 6 − (−25) = 6 + 25 = 31
Therefore, the correct choice is B) 31 feet.
Learn more about depth here:
brainly.com/question/20070144
#SPJ1
a rectangular auditorium seats 2244 people. The number of seats in each row exceeds the number of rows by 7. Find the number of seats in each row
Answers
Number of seats in each row is 51 given that a rectangular auditorium seats 2244 people and number of seats in each row exceeds the number of rows by 7. This can be obtained by assuming the value of number of seats in each row, forming quadratic equation and using quadratic formula to find root.
Find the number of seats in each row:
Here in the question it is given that,
a rectangular auditorium seats 2244 peoplenumber of seats in each row exceeds the number of rows by 7We have to find the number of seats in each row.
Let us assume that the number of seats in each row be x.
From the given statement, number of seats in each row exceeds the number of rows by 7, we can write that,
Number of seats in one row = Number of rows + 7
x = Number of rows + 7
⇒ Number of rows = x - 7
Total number of seats in the auditorium can be written as,
⇒ (Number of seats in one row)(Number of rows) = Total number of seats
(x)(x - 7) = 2244
x² - 7x = 2244
⇒ x² - 7x - 2244 = 0
By using quadratic formula we can find the root,
x = (-b ± √b² - 4ac)/2a
here in the question, a = 1, b = -7, c = -2244
√b² - 4ac = √(-7)² - 4(1)(-2244)
√b² - 4ac = √49 + 8976
√b² - 4ac = √9025
√b² - 4ac = 95
x = (-b ± √b² - 4ac)/2a
x = (7 ± 95)/2
x = 102/2 or x = -88/2
⇒ x = 51 or x = -44
Hence number of seats in each row is 51 given that a rectangular auditorium seats 2244 people and number of seats in each row exceeds the number of rows by 7.
Learn more about quadratic formula here:
brainly.com/question/26926523
#SPJ9
What the the Quotient 7/12 divided by 2/5
Answers
Answer:35/24
Step-by-step explanation:
7/12 ➗ 2/5
Next step we change divide sign to multiplication,with the numerator and denominator of the right hand fraction inverted
7/12 x 5/2
(7x5)/(12x2)
35/24
The quotient of 7/12 divided by 2/5 is 35/24.
To divide fractions, you need to multiply the first fraction by the reciprocal (or the multiplicative inverse) of the second fraction.
The reciprocal of a fraction is obtained by swapping the numerator and the denominator.
So, to find the quotient of 7/12 divided by 2/5, you multiply 7/12 by the reciprocal of 2/5, which is 5/2.
Here are the steps:
Write down the first fraction: 7/12
Write down the reciprocal of the second fraction: 5/2
Multiply the first fraction by the reciprocal: (7/12) x (5/2)
Multiply the numerators: 7 x 5 = 35
Multiply the denominators: 12 x 2 = 24
Simplify the fraction, if possible: 35/24
Therefore, the quotient of 7/12 divided by 2/5 is 35/24.
Learn more about fraction click;
https://brainly.com/question/10354322
#SPJ6
PLEASE HELP I WILL GIVE BRAINLIEST!!
14. Katherine and Christine work at the same restaurant. Each week, Katherine works 5 more
hours than Christine Katherine earns $7.00 per hour and Christine earns $8.00 per hour.
a) Write a simplified expression to represent the total number of hours Katherine and
Christine work in one week.
b) Write a simplified expression to represent the total amount they earn in one week.
c) Suppose Christine and Katherine worked 9 hours last week. What was the total amount
the girls earned last week?
Answers
Answer:.
Step-by-step explanation:
Find the value of x, 6,4, 3x, 4x+1

Answers
Answer:
If two chords intersect in a circle, then the product of the segments of one chord equals the product of the segments of the other chord.
6(3x) = 4(4x + 1)
18x = 16x + 4
2x = 4
x = 2