Lillian has $900 in a savings account that earns 6% interest per year. The interest is not compounded. How much interest will she earn in 3 years?
Answers
Answer:
$162
Step-by-step explanation:
Interest (non-compounding) = principal x rate x time (in years)
I = 900(.06)(3)
I = 162
Answer:
$162
Step-by-step explanation:
if the interest is not compounded, its a simple interest.
simple interest formula = (PRT)/100 ......where p is the amount of money, r is rate of interest and t is time
using the formula : ($900 * 6% * 3 years)/100
: $162
∵ Lillian earns $162 in 3 years.
Related Questions
Find the sum of the first 10 terms of an arithmetic sequence with an eighth term of 8.2 and a common difference of 0.4.
Answers
The sum of first 10 terms is 72.
Concept: Arithmetic Progression (AP) is a sequence of numbers in order, in which the difference between any two consecutive numbers is a constant value. It is also called Arithmetic Sequence.
Arithmetic Progression Formula
= an - a. nth term of an AP: an = a + (n - 1)d. Sum of n terms of an AP: Sn = n/2(2a+(n-1)d) = n/2(a + l), where l is the last term of the arithmetic progression.
Given:
Eighth term is 8.2
Common difference is 0.4
a(8) = 8.2
a + 7d = 8.2
Since d = 0.4
a + 7(0.4) =8.2
a = 5.4
Sum of 10 terms = n/2 (2a+(n-1)d)
= 5(2*5.4 + 9*0.4)
=5(10.8 +3.6)
Sum=72
For more information about arithmetic progression, visit
https://brainly.com/question/6561461
#SPJ4
A cylindrical metal pipe has a diameter of 8.4 millimeters and a height of 10 millimeters. A hole cut out of the center has a diameter of 6 millimeters. A smaller cylinder is cut out of a larger cylinder. The smaller cylinder has a diameter of 6 millimeters. The larger cylinder has a diameter of 8.4 millimeters. Both cylinders have a height of 10 millimeters. What is the volume of metal in the pipe? Use 3.14 for and round the answer to the nearest tenth of a cubic millimeter. 282.6 mm3 271.3 mm3 553.9 mm3 836.5 mm3
Answers
Answer:
its b
Step-by-step explanation:
got it right on edge
The volume of the metal in the cylinderical pipe given the dimensions of the larger and smaller cylinders is 271.30 mm³.
What is the volume of the cylinder?A cylinder is a three-dimensional object. It is a prism with a circular base.
Volume of a cylinder = nr^2h
Where:
n = 22/7 r = radius = diameter / 2The volume of the metal in the cylinderical pipe = 3.14 x 10 x [(8.4/2)² - 6/2)²] = 271.30 mm³
To learn more about to determine the volume of a cylinder, check: https://brainly.com/question/9624219
#SPJ2
the amount of time it takes john to wait in line at the bank is continuous and uniformly distributed between 7 minutes and 17 minutes. what is the probability that it takes john between 9 and 12 minutes to wait in line at the bank?
Answers
The probability of John waiting is
0.333.
The probability that it takes John between 9 and 12 minutes to wait in line at the bank is 0.333.
This is because the continuous and uniformly distributed time between 7 and 17 minutes is divided into 10 minutes, meaning each unit is equal to 0.1. Therefore,
the probability of John waiting between 9 and 12 minutes is 3 units of 0.1 which is 0.333.
Learn more about continuous and uniformly distributed
brainly.com/question/28348710
#SPJ11
1. If A is a subset of B, then A is a proper subset of B. 2. The union of any set A and its complement is the universal set.
Answers
If A is a subset of B, it does not necessarily mean that A is a proper subset of B. The union of any set A and its complement is indeed the universal set.
1. False: If A is a subset of B, it does not necessarily mean that A is a proper subset of B. A proper subset is a subset that contains some, but not all, elements of the superset. In other words, if A is a proper subset of B, it means that there exists at least one element in B that is not in A. However, if A is simply a subset of B, it is possible for A and B to have the same elements, making them equal sets.
For example, let's consider two sets:
A = {1, 2}
B = {1, 2, 3}
In this case, A is a subset of B because every element in A (1 and 2) is also in B. However, A is not a proper subset of B since there are no elements in B that are not in A. Therefore, statement 1 is false.
2. True: The union of any set A and its complement is indeed the universal set. The complement of a set A, denoted as A', consists of all elements that are not in A but are in the universal set U. When we take the union of A and its complement, we are effectively combining all elements from A and all elements not in A.
Let's consider a set A and its complement A' within a universal set U. The union of A and A' is denoted as A ∪ A' and can be represented as U. This is because every element in the universal set U is either in A or not in A (in A').
For example, let's consider the following sets:
U = {1, 2, 3, 4, 5}
A = {1, 2}
The complement of A, A', would be {3, 4, 5}. The union of A and A' (A ∪ A') is {1, 2} ∪ {3, 4, 5}, which is equal to U: {1, 2, 3, 4, 5}. Thus, the union of any set A and its complement is indeed the universal set. Therefore, statement 2 is true.
Learn more about universal set:
https://brainly.com/question/29478291
#SPJ11
the blue segment below is a diameter of 0. What is the length of the radius of the circle ?

Answers
Answer:
4. 1 units
Step-by-step explanation:
A diameter of a circle is equal to 2 of its radiuses. Just simply divide the diameter by 2.
find the radian measure of the central angle of a circle of radius r that intercepts an arc of length s.
Answers
The central angle in radians is given by θ = s/r, where s is the arc length and r is the radius of the circle
For given question,
we need to find the radian measure of the central angle of a circle of radius r.
The central angle intercepts an arc of length s.
Let θ be the central angle in radians.
We know that the arc length of circle of radius r is,
s = r × θ
where s is the arc length
r is the radius of the circle
θ is the central angle measured in radians
From above equation,
we have, θ = s ÷ r
Therefore, the central angle in radians is given by θ = s/r, where s is the arc length and r is the radius of the circle
Learn more about the arc length here:
https://brainly.com/question/16403495
#SPJ4
find slope of line passing through the points AB is -1/2 then find the slope of line BC
Answers
Answer:
Slope of BC = 1/2
Step-by-step explanation:
Given collinear points A, B and C
slope of the line AB = 1/2
principal=10000 Rate=7% time=20 years
Answers
Answer:
p= 10000
r= 7
t=20 yrs
I= ?
We know that,
I= P× T × R /100
=10000× 7×20/100
= 14000,,
A line is perpendicular to y = -1/5x + 1 and intersects the point negative (-5,1) what is the equation of this perpendicular line?
Answers
Answer: y = 5x + 26
Step-by-step explanation:
To find the equation of a line that is perpendicular to the given line y = -1/5x + 1 and passes through the point (-5, 1), we need to determine the slope of the perpendicular line. The given line has a slope of -1/5. Perpendicular lines have slopes that are negative reciprocals of each other. So, the slope of the perpendicular line will be the negative reciprocal of -1/5, which is 5/1 or simply 5. Now, we have the slope (m = 5) and a point (-5, 1) that the perpendicular line passes through.
We can use the point-slope form of a linear equation to find the equation of the line:
y - y1 = m(x - x1)
Substituting the values, we get:
y - 1 = 5(x - (-5))
Simplifying further:
y - 1 = 5(x + 5)
Expanding the brackets:
y - 1 = 5x + 25
Rearranging the equation to the slope-intercept form (y = mx + b):
y = 5x + 26
Therefore, the equation of the perpendicular line that passes through the point (-5, 1) is y = 5x + 26.
convert 9/4 into a mixed number
Answers
8/4 = 2
so the mixed number is 2 1/4
What is the product of 3a + 5 and 2a2 + 4a – 2?
Answers
Answer:
9a+5
Step-by-step explanation:
3a+5 and 2a2+4a-2= 6a+3a+5 =9a+5
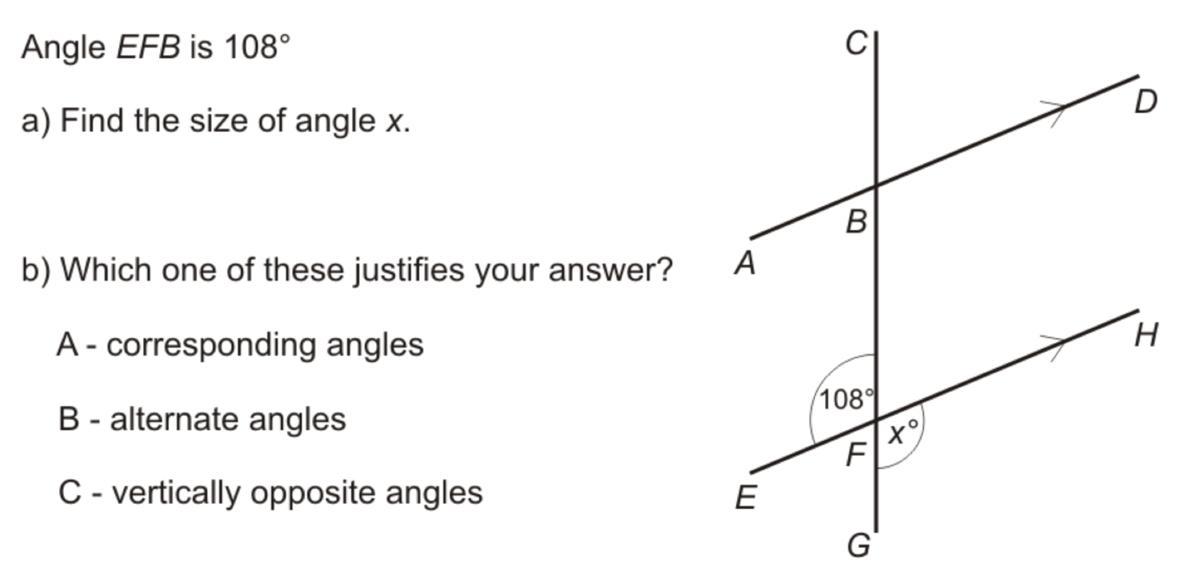
Angle EFB Is 108
a) Find the size of angle x.
b) Which one of these justifies your answer?
Answers
Answer 108 and c
Step-by-step explanation:
for question A the angle is a vertically opposite angle so that means that the answer is 108 degrees for B is C because the angles are vertically opposite .
Can a triangle have sides that measure 5 cm 12 cm 13 cm?
Answers
Yes , the given statement is true , after implying Pythagoras theorem we conclude that the sides can be 5 cm 12 cm 13 cm.
We can use Pythagoras theorem to check whether the sides of a triangle can measure 5 cm 12 cm 13 cm or not .
The sum of square of two smaller sides should be equal to the third side.
13² = 12² + 5²
13² = √144 + 25
13² =√169
13² = 13
Therefore, we can conclude that the sides of a triangle can be 5 cm 12 cm 13 cm.
Pythagoras theorem states that the sum of smaller sides could be equal to the larger side. AC² = AB² + BC².
To learn more about Pythagoras
brainly.com/question/10174253
#SPJ4
express the confidence interval ( 149.2 , 206.4 ) in the form of ¯ x ± m e
Answers
The confidence interval (149.2, 206.4) can be written as ¯x ± me, where ¯x = 177.8 and me = 28.6. The sample mean (¯x) is the midpoint of the confidence interval
To express the confidence interval (149.2, 206.4) in the form of ¯x ± me, we need to calculate the sample mean (¯x) and the margin of error (me).
The sample mean (¯x) is the midpoint of the confidence interval and can be calculated by taking the average of the upper and lower bounds of the interval:
¯x = (149.2 + 206.4) / 2 = 177.8
Next, we calculate the margin of error (me) by finding the half-width of the confidence interval:
me = (206.4 - 149.2) / 2 = 28.6
Therefore, the confidence interval (149.2, 206.4) can be expressed in the form of ¯x ± me as:
¯x ± me = 177.8 ± 28.6
Hence, the confidence interval (149.2, 206.4) can be written as ¯x ± me, where ¯x = 177.8 and me = 28.6.
Learn more about confidence interval here
https://brainly.com/question/20309162
#SPJ11
Solve for T in the problem d = r * t
Answers
Answer: the T means "time"
Step-by-step explanation:
distance = rate * time
hope this helps :)
PLEASE HELP WILL MARK BRAINLIEST

Answers
Answer: D 12
Step-by-step explanation:
Can anyone answer this question ?

Answers
X2=-radical 6/3--->-0.816
what linear function can be represented by the set of ordered pairs? {(−4, 15), (0, 5), (4, −5), (8, −15)} enter your answer in the box. f(x)=
Answers
Answer:
f(x) = -2.5x +5
Step-by-step explanation:
You want the linear function f(x) that is represented by the ordered pairs ...
{(−4, 15), (0, 5), (4, −5), (8, −15)}
SlopeThe slope of the line can be found using the formula ...
m = (y2 -y1)/(x2 -x1)
m = (5 -15)/(0 -(-4)) = -10/4 = -2.5
InterceptThe y-intercept of the line is given by the point (0, 5).
Slope-intercept formThe equation of the line in slope-intercept form is ...
f(x) = mx +b . . . . . . . where m is the slope, and b is the y-intercept
For the values we've identified, the equation of the line is ...
f(x) = -2.5x +5
<95141404393>

find the solution to following system using substitution or elimination
y = -x + 10
y = 7x + 2
A. (1,9)
B. ( 3/2 , 17/2)
C. (9,65)
D. (1, -1/7)
Answers
Answer:
the answer is (1,9)
Step-by-step explanation:
5.15 Find what percent one number is of another: word problems 498
After a month of successful fundraising, David and his classmates voted on whether to donate
the money they had raised to hunger relief or to environmental causes. Out of 27 votes, 27
were for hunger relief. What percentage of the votes were for hunger relief
Write your answer using a percent sign (%).
Submit
Answers
Answer:
100%
Step-by-step explanation:
If all 27 votes for hunger relief, that would be 100% or all of them.
Let L = {a(^i)bbw|w ∈ {a, b} ∗ and the length of w is i}.
(a) Give two strings that are in L.
(b)Give two strings over the same alphabet that are not in
L.
(c)Give the state diagram for a determin
Answers
(a) Strings in L: "abb", "aabbb". (b) Strings not in L: "aabb", "bb".
(c) State diagram for a deterministic Turing Machine with 10 states is given below.
(a) Two strings that are in L are:
1. `abb` (Here, i = 0, and w is an empty string).
2. `aabbb` (Here, i = 2, and w = "aa").
(b) Two strings over the same alphabet that are not in L are:
1. `aabb` (Here, the length of w is 2, but there are more than two 'a's before the 'bb').
2. `bb` (Here, the length of w is 0, but there are 'b's before the 'bb', violating the condition).
(c) Here is the state diagram for a deterministic Turing Machine with 10 states that decides L:
```START --> A --> B --> C --> D --> E --> F --> G --> H --> ACCEPT
a b b a a b b a b
| | | | | | | | |
v v v v v v v v v
REJECT REJECT REJECT A E F REJECT REJECT REJECT
| | | | | | | | |
v v v v v v v v v
REJECT REJECT REJECT REJECT REJECT REJECT G H REJECT
| | | | | | | | |
v v v v v v v v v
REJECT REJECT REJECT REJECT REJECT REJECT REJECT REJECT REJECT```
In this state diagram, the machine starts at the START state and reads input symbols 'a' or 'b'. It transitions through states A, B, C, D, E, F, G, and H depending on the input symbols.
If the machine reaches the ACCEPT state, it accepts the input, and if it reaches any of the REJECT states, it rejects the input. The machine accepts inputs of the form `a^i b^bw` where the length of w is i.
Learn more about length here: https://brainly.com/question/30625256
#SPJ11
The complete question is:
Let L = {a(^i)bbw|w ∈ {a, b} ∗ and the length of w is i}.
(a) Give two strings that are in L.
(b)Give two strings over the same alphabet that are not in L.
(c)Give the state diagram for a deterministic Turing Machine that decides L. To receive full credit, your Turing Machine shall have no more than 10 states.
linear equation that has a slope of 5/6 and y-intercept of 14
Answers
Answer:
Slope-intercept form is y = 5/6x + 14
If 7x + 6y = 8 is a true equation, what would be the value of 7x + 6y - 5?
Answers
Answer:
I’m going to guess and say that it’s 3? Not sure sorry!
Cameron has 58 m of fencing to build a three-sided fence around a rectangular plot of land that sits on a riverbank. (The fourth side of the enclosure would be the river.) The area of the land is 380 square meters. List each set of possible dimensions (length and width) of the field.
Answers
Answer:
The list of set of dimensions for fencing the building around a rectangular plot of land is 14.5 meters and 29 meters.
Area of a rectangle
area of rectangle = lw
where
l = length
w = width
Therefore,
perimeter = 2w+ l
58 = 2w + l
l = 58 - 2w
Hence,
area = w(58 - 2w)
380 = 58w - 2w²
-2w² + 58w - 380 = 0
-w² + 29w - 190 = 0
The dimension w can be found as follows;
w = - b / 2a
where
a = -1
b = 29
w = - 29 / 2 × -1
w = 14.5 meters
Then,
l = 58 - 2w
l = 58 - 2(14.5)
l = 29 meters
Therefore, the dimensions are 14.5 meters and 29 meters.
learn more on rectangle here: brainly.com/question/15536011
#SPJ4
A mine worker discovers an ore sample containing 500 mg of radioactive material. it is discovered that radioactive material has a half-life of 1 day. Find the amount of radioactive material in the sample at the beginning of the 7th day
Answers
The amount of radioactive material remaining after 6 days is 7.8 mg
What is radioactive decay?Radioactive decay is the process by which an unstable atomic nucleus loses energy by radiation.
The amount of time that it takes one half of the atoms present to decay is called “half-life.
The half life is 1 day
2 days = 1/4
3 days = 1/8
4 days = 1/16
5 days = 1/32
6 days = 1/64
Since the question says on the beginning of 7th days , we are going to stop at 6th day
Therefore on the 7th day
500 × 1/64
= 7.8 mg will remain.
learn more about radioactive decay from
https://brainly.com/question/9932896
#SPJ1
What does y equal?
Will Give Brianlest!

Answers
Answer:
\(\boxed{\tt y=48}\)
Step-by-step explanation:
\(\tt \cfrac{3}{16}=\cfrac{9}{y}\)
Cross multiply:-
\(\tt 3 \times y=(9)\times (16)\)
\(\tt 3y=144\)
Divide both sides by 3:-
\(\tt \cfrac{3y}{3}=\cfrac{144}{3}\)
Simplify:-
\(\tt y=48\)
_________________
Hope this helps!
Answer:y=48 I hope this is helpful good luck have a good day
Step-by-step explanation:
3/16 = 9/y
Determine the defined range
3/16=9/y y=0 cross out the equal sign y=0
Simplify the equation using cross-multiplication
3y=144
Divide both sides of the equation by 3
y=48
Check if the solution is in the defined range
What is the answer
5 3/5 - 3 14/16
Answers
Answer:
138/80
Step-by-step explanation:
5×5+3/5-3×16+14/16
28/5-62/16
28×16/5×16-62×5/16×5
448/80-310/80
448-310/80
138/80
Which is the cosine ratio of angle A?

Answers
Answer:
The cosine ratio of angle A is 28/197
Step-by-step explanation:
The cosine of the angle is the adjacent (to the angle) side and the hypotenuse
So, in this case, the side AC and the hypotenuse AB
Hence, cosine ratio of angle A is 28/197
Write 3 expressions that can be used to find angle C.

Answers
Answer:
\(sin^{-1}(x) = \frac{55}{73} \\\\cos^{-1}(x) = \frac{48}{73} \\\\tan^{-1}(x) = \frac{48}{55}\)
Step-by-step explanation:
Since you're finding the angle, you use the inverse of sin, cos, and tan.
Suppose that A and B are two independentevents for which P(A)=0.3 and P(B)=0.69. Find each of the follon A. P(A∣B)= B. P(B∣A)= C. P(A and B)= D. P(A or B)= Note: You can eam partia credif on this problem.
Answers
A. P(A|B) = 0.3; B. P(B|A) = 0.69; C. P(A and B) = 0.207; D. P(A or B) = 0.783.
To solve the problem, we can use the formulas for conditional probability and the probability of independent events: A. P(A|B) = P(A and B) / P(B). Since A and B are independent events, P(A and B) = P(A) * P(B). Thus, P(A|B) = P(A) * P(B) / P(B) = P(A) = 0.3. B. P(B|A) = P(A and B) / P(A). Using the same reasoning as above, P(B|A) = P(B) = 0.69. C. P(A and B) = P(A) * P(B) = 0.3 * 0.69 = 0.207. D. P(A or B) = P(A) + P(B) - P(A and B). Since A and B are independent, P(A and B) = P(A) * P(B).
Therefore, P(A or B) = P(A) + P(B) - P(A) * P(B) = 0.3 + 0.69 - 0.207 = 0.783. So, the answers are: A. P(A|B) = 0.3; B. P(B|A) = 0.69; C. P(A and B) = 0.207; D. P(A or B) = 0.783.
To learn more about P(A|B) click here: brainly.com/question/1748401
#SPJ11