Let X1, X2, ..., Xm be a random sample from a population with mean mu1 and variance of sigma1^2=, and let Y1, Y2, ... , Yn be a random sample from a population with mean mu2 and variance sigma2^2, and that X and Y samples are independent of one another. Which of the following statements are true? Xbar is normally distributed with expected value mu1 and variance sigma1^2/m Ybar is normally distributed with expected value mu2 and variance sigma2^2/m Xbar-Ybar is normally distributed with expected value mul-mu2 and variance (sigma1^2/m+sigma2^2/n). Xbar-Ybar is an unbiased estimator of mul-mu2. All of the above statements are true.
Answers
Let X₁, X₂, ..., Xₙ be a random sample from a population with mean mu₁ and variance of sigma₁² then All of the above statements are true.
a) Xbar is normally distributed with expected value mu₁ and variance sigma₁²/m:
According to the Central Limit Theorem, when the sample size is large enough, the sampling distribution of the sample mean (X bar) approximates a normal distribution. The expected value of X bar is mu₁, the mean of the population, and the variance of X bar is sigma₁²/m, where sigma₁² is the variance of the population and m is the sample size.
b) Ybar is normally distributed with expected value mu₂ and variance sigma₂²/n:
Similar to Xbar, Ybar follows a normal distribution by the Central Limit Theorem. The expected value of Ybar is mu², the mean of the population, and the variance of Ybar is sigma₂²/n, where sigma₂² is the variance of the population and n is the sample size.
c) Xbar - Ybar is normally distributed with expected value mu₁ - mu₂ and variance (sigma₁²/m + sigma₂²/n):
Since Xbar and Ybar are independent, the difference Xbar - Ybar follows a normal distribution. The expected value of Xbar - Ybar is mu₁ - mu₂, and the variance of Xbar - Ybar is (sigma₁²/m + sigma₁²/n), where sigma₁² is the variance of the X population, sigma₂² is the variance of the Y population, m is the sample size for X, and n is the sample size for Y.
d) Xbar - Ybar is an unbiased estimator of mu₁ - mu₂:
An estimator is unbiased if its expected value equals the true value being estimated. Since the expected value of Xbar - Ybar is mu₁ - mu₂, it is an unbiased estimator of the difference in means, mu₁ - mu₂.
To know more random sample about click here :
https://brainly.com/question/28942677
#SPJ4
Related Questions
Find the perimeter of each figure in feet, 48 in 3yd 5ft 1yd .

Answers
Answer:
Step-by-step explanation:
Remark
First of all, all the units must be the same. Inches is probably the best unit to use.
Second the base line at the bottom must be completed. How long is it
Givens
Left side = 48 inches
Top = 3 yards
1 yard is 36 inches.3 yard is 3* 36 = 108 inches.Right side = 5 feet.
1 foot = 12 inches5 feet = 12 * 5 = 60 inchesBottom = 1 yard + top
Bottom = 1 yard + 3 yards
Bottom = 4 yards
1 yard = 36 inches4 yards = 144 inchesPerimeter = 144 + 60 + 108 + 48
Perimeter = 360 Inches.
Answer
Perimeter = 360 inches
Perimeter = 360 / 12 = 30 feet There are 12 inches in a foot
Perimeter = 360 / 36 = 10 yards. There are 36 inches in a yard
The question does not specify the units. Probably inches would work, but if a computer is marking your answer and you get it wrong, you are going to have to try the other two answers in turn.
5. A 50-inch piece of wire is bent into the shape of a rectangle. Find the dimensions of the rectangle
of maximum area that can be formed from the wire,
Answers
Answer:
length = 12.5 in, width = 12.5 in, Area = 156.25 in²
Step-by-step explanation:
To get the maximum area, the wire can be shaped into a square. We can say that the length and width of the rectangle must be equal to each other, and call this value "x".
Therefore, we can write an equation for the perimeter:
2x + 2x = 50 4x = 50 x = 12.5The area of the rectangle is calculated using the formula:
A = lwOr in our case, the area of the rectangle is the area of a square:
A = x²Substitute x = 12.5 into this equation.
A = (12.5)² A = 156.25The maximum area that can be formed from the wire is 156.25 in², and the dimensions of the rectangle are 12.5 x 12.5 in.
Use the drop-down menus and the image to complete these statements about prokaryotes. prokaryotes a nucleus surrounding their chromosome of dna. prokaryotes are simple cells than eukaryotes. prokaryotes have a outside their cell membrane that gives protection and support. prokaryotes will often move by a tail-like .
Answers
Eukaryotic cells have a true membrane-bound nucleus and prokaryotes do not.
What are eukaryotic and prokaryotic cells?Eukaryotic cells are larger than prokaryotic cells and have a “true” nucleus, membrane-bound organelles, and rod-shaped chromosomes. The nucleus houses the cell's DNA and directs the synthesis of proteins and ribosomes.
All cells have a plasma membrane, ribosomes, cytoplasm, and DNA. Prokaryotic cells lack a nucleus and membrane-bound structures. Eukaryotic cells have a nucleus and membrane-bound structures called organelles.
So..the answer should be Eukaryotic cells have a true membrane-bound nucleus and prokaryotes do not.
To know more about Cells follow
https://brainly.com/question/13920046
Answer:
Prokaryotes
✔ do not have
a nucleus surrounding their chromosome of DNA.
Prokaryotes are
✔ more
simple cells than eukaryotes.
Prokaryotes have a
✔ cell wall
outside their cell membrane that gives protection and support.
Prokaryotes will often move by a tail-like
✔ flagellum
.
Step-by-step explanation:
Dominic is stacking legos to make a tower. He takes a break when the tower is 4 1/2 feet tall, which is 3/8 of the height of the tower he wants to build. How tall is the tower when finished?
Answers
Answer:
Tower is 9 ft tall when it is finished.
Step-by-step explanation:
Given that:
Height of the tower when Dominic takes a break = \(4\frac{1}{2}\) feet
The height of the tower as built by Dominic = \(\frac{3}8\) of the total height
Let the total height of the tower to be built = \(x\) feet
Let us have a look at the method to convert mixed fraction to a fractional number.
\(a\dfrac{b}{c} = \dfrac{a\times c +b}c\\\Rightarrow 4\dfrac{1}{2} = \dfrac{4\times 2 +1}{2}=\dfrac{9}2\)
As per question statement, \(\frac{3}8\) of the total height is equal to \(4\frac{1}{2}\) feet.
We can write the equation as:
\(\dfrac{3}{8}x = \dfrac{9}{2}\\\Rightarrow x = \dfrac{9}{2}\times \dfrac{8}{3}\\\Rightarrow x = \dfrac{72}{6}\\\Rightarrow x = \bold{9\ ft}\)
Therefore, tower is 9 ft tall when it is finished.
Determine whether each of the following sequences are arithmetic, geometric or neither. If arithmetic, state the common difference. If geometric, state the common ratio.
4, 13/3, 14/3, 5, 16/3, …
Is the answer: Neither?
Answers
\(\qquad\qquad\huge\underline{{\sf Answer}}\)
\( \textbf{Let's see if the sequence is Arithmetic or Geometric :} \)
\( \textsf{If the difference between successive terms is } \) \( \textsf{equal then, the terms are in AP} \)
\( \sf{ \dfrac{14}{3}- \dfrac{13}{3} = \dfrac{1}{3}} \)\( \sf{ {5}{}- \dfrac{14}{3} = \dfrac{15-14}{3} =\dfrac{1}{3}} \)\( \textsf{Since the common difference is same, } \) \( \textsf{we can infer that it's an Arithmetic progression} \) \( \textsf{with common difference of } \sf \dfrac{1}{3} \)
Answer:
Arithmetic with common difference of \(\sf \frac{1}{3}\)
Step-by-step explanation:
\(\textsf{Given sequence}=4, \dfrac{13}{3}, \dfrac{14}{3}, 5, \dfrac{16}{3},...\)
If a sequence is arithmetic, the difference between consecutive terms is the same (this is called the common difference).
If a sequence is geometric, the ratio between consecutive terms is the same (this is called the common ratio).
\(\sf 4\quad \overset{+\frac{1}{3}}{\longrightarrow}\quad\dfrac{13}{3}\quad \overset{+\frac{1}{3}}{\longrightarrow}\quad \dfrac{14}{3}\quad \overset{+\frac{1}{3}}{\longrightarrow}\quad 5\quad \overset{+\frac{1}{3}}{\longrightarrow}\quad \dfrac{16}{3}\)
As the difference between consecutive terms is \(\sf \frac{1}{3}\) then the sequence is arithmetic with common difference of \(\sf \frac{1}{3}\)
General form of an arithmetic sequence: \(\sf a_n=a+(n-1)d\)
where:
\(\sf a_n\) is the nth terma is the first termd is the common difference between termsGiven:
a = 4\(\sf d=\dfrac{1}{3}\)So the formula for the nth term of this sequence is:
\(\implies \sf a_n=4+(n-1)\dfrac{1}{3}\)
\(\implies \sf a_n=\dfrac{1}{3}n+\dfrac{11}{3}\)
archer can paint a room in 4 hours, while ollie can do it in 3. if they work together, how long will it take them to paint two rooms? express your answer as a decimal rounded to the nearest tenth.
Answers
If Archer can paint a room in 4 hours, while Ollie can do it in 3 hours. If they work together then it will take 206 minutes to paint two rooms.
What is the relation between work and time?
Work Problems are word problems that involve different people or entities doing work but at different rates.
Work = Efficiency x Time
According to the given question:
Archer paints a room in = 4 hours
Work done by him in an hour =1/4
Ollie paints a room in = 3 hours
Work done by him in an hour = 1/3
So, work done by them in an hour W = (1/4 +1/3)= 7/12.
They both will complete the work in = 1/W
= 1/7/12
= 12/7 hours
≈ 103 minutes
Therefore it take 103 minutes to paint one room together.
To paint two rooms it will take 103 x 2 = 206 minutes together.
To know more about work problems visit
https://brainly.com/question/14675081
#SPJ4
A clay specimen, 25 mm thick, has been tested in an oedometer apparatus with two way rainage, and it is observed that 50% of the consolidation settlement occurs in 1 hour. A ayer of the same clay is observed to settle 10 mm in 10 years and after many years to settle (total primary consolidation) by 35 mm. Determine the thickness of the clay layer if it drains only from upper surface
Answers
The thickness of the clay layer, which drains only from the upper surface, can be determined based on the consolidation settlement observations. With 50% of consolidation settlement occurring in 1 hour for a 25 mm thick specimen, and a total primary consolidation settlement of 35 mm occurring over many years, the thickness of the clay layer is approximately 87.5 mm.
The consolidation settlement of a clay specimen can be used to estimate the thickness of a clay layer that drains only from the upper surface. In this case, the observed settlement data provides valuable information.
Firstly, we know that 50% of the consolidation settlement occurs in 1 hour for a 25 mm thick clay specimen. This is an important parameter for calculating the coefficient of consolidation (Cv) using Terzaghi's theory. From the Cv value, we can estimate the time required for full consolidation settlement.
Secondly, we are given that the same clay settles 10 mm over 10 years and eventually settles a total of 35 mm over a longer period. This long-term settlement is known as the total primary consolidation settlement. By comparing this settlement value with the settlement data from the oedometer test, we can determine the thickness of the clay layer.
To calculate the thickness, we can use the concept of the consolidation settlement ratio. The ratio of the total primary consolidation settlement to the consolidation settlement at 50% completion is equal to the ratio of the total thickness to the thickness at 50% completion. Applying this ratio, we can determine that the thickness of the clay layer, which drains only from the upper surface, is approximately 87.5 mm.
To learn more about thickness click here: brainly.com/question/23622259
#SPJ11
Ingrid has 14.4 meters of string to hang 5 pennants and a banner at her school. She needs 0.65 meter of string for the banner and the same length string for each pennant. What length of string will be used to hang each pennant? Write and solve a two-step equation. Let s represent the length of string used to hang each pennant.
Answers
Answer:
5s + 0.65 = 14.4
- 0.65 - 0.65
______________
5s = 13.75
___. ___
5 5
s = 2.75 meters of string for each pennant
Explanation:
s represents the length of string required for each pennant.
We know that Ingrid is using a total of 14.4 meters of string to hang a banner and 5 pennants.
We also know that out of that 14.4 meters, 0.65 meters is used to hang the banner. The rest of the string left is equally distributed among the 5 pennants.
So, therefore, we have a constant of 0.65 and a coefficient of 5 with variable, s.
Next, we solve this by first isolating the constant by subtracting 0.65 on both sides.
Then. we isolate the variable by dividing 5 into both sides.
So, s = 2.75 meters of string for each pennant
help plz !! Which is the graph of an even monomial function?
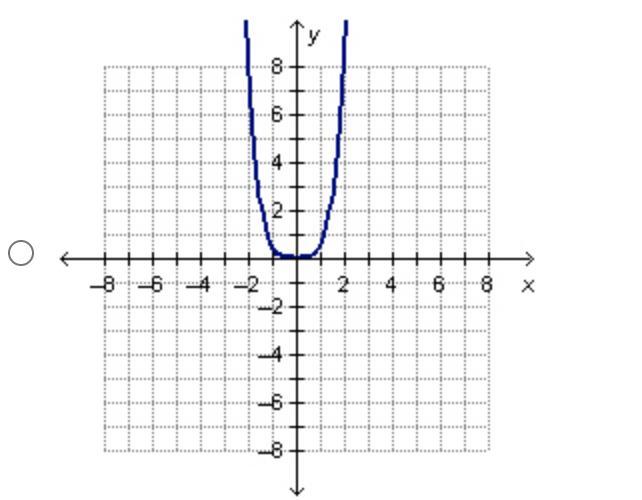



Answers
Answer:
Imagie 1 and 2
monomial function graph look like this
<3 ily
Red

Answer:
The first image
Explanation:
Hope you have a great day!
What is the area of the parallelogram?
1
115 cm
21 cm
1
20 cm

Answers
Answer:
answer: 300
Step-by-step explanation:
the area of the parellologram is found just by doing base × height! So our base is 20 and our height is 15 so now that we know our base and height. all we have to do is multiply them so
20 x 15 = 300 so 300 is our answer! Hope that helps you!
the area of a square is 4x²+12x+9 square units. Whick expression represent the length of the side?
Answers
Answer:
the length of the square is (2x+3)
Step-by-step explanation:
hope it helps<333
In the image below, a = 8 cm and b = 9 cm.
What is the surface area of the square pyramid?
144 square cm
196 square cm
225 square cm
369 square cm

Answers
Answer:
225
Step-by-step explanation:
first the square
9*9 = 81
then the triangle
a is 8
triangles are l*w/2 so 8*4.5/2
8*4.5 = 36/2 = 18
There are 8 of these triangles
18*8 is 144
144+81 = 225
The surface area of the square pyramid is approximately `196` square cm.
What is Surface Area?The quantity of space enclosing a three-dimensional shape's exterior is its surface area.
We can use the Pythagorean theorem to find the slant height of the pyramid:
\($$l = \sqrt{a^2 + \left(\frac{b}{2}\right)^2} \\= \sqrt{8^2 + \left(\frac{9}{2}\right)^2} \\= \sqrt{64+\frac{81}{4}} \\= \frac{\sqrt{433}}{2}$$\)
So, the lateral area of the pyramid is the area of the four triangles with base `b` and height `l`, which is:
\($$A_{lat} = 4\cdot\frac{1}{2}b\cdot l \\= 4\cdot\frac{1}{2}\cdot 9 \cdot \frac{\sqrt{433}}{2} \\= 27\sqrt{433}$$\)
So, The area of the base of the pyramid is a² then
\($$A = A_{lat} + a^2$$\)
= = 27√433 + 8²
= 27√{433} + 64
= 196.4 cm²
Therefore, the surface area of the square pyramid is approximately `196` square cm.
Learn more about Surface Area here:
https://brainly.com/question/29298005
#SPJ3
parallel perpendicular or neither

Answers
Answer:
Parallel
Step-by-step explanation:
Line A can be simplified to 1/5x = y.
Line B can be simplified to y = 1/5x + 16.
They both have the same slope, 1/5, so they will be parallel.
Answer:
Parallel
Step-by-step explanation:
Same thing as the last one. Put it in \(y=mx+b\)
A: \(y=1/5x\)
and
B: \(y=1/5x+16\)
These lines are parallel because they have the same slopes, but different y-intercepts.
FIND Arc length of CD

Answers
The measure of the length of arc with a cental angle of 50 degree and radius 7cm is approximately 35π/18 cm.
What is the arc length of the circle?An arc length is simply the distance between two points along a section of a curve in a circle.
It can be expressed as:
Length of arc = θ/360 × 2πr
Where θ is the central angle in degree and r is the radius.
From the diagram:
Central angle θ = 50 degree
Radius r = 7 cm
Arc length = ?
Plug the given values into the above formula and solve for the arc length:
Length of arc = θ/360 × 2πr
Length of arc = 50/360 × 2 × π × 7cm
Length of arc = 35π/18 cm
Therefore, the arc length measures 35π/18 cm.
Learn more about arc length here: brainly.com/question/32035879
#SPJ1
i really need help with this , if anyone can help :)

Answers
Answer:
a. 14 + x
b. There are several ways to write this, 6y, 6(y)
Step-by-step explanation:
Look for key words when you do these types of questions!
For addition, add, sum, greater than, etc.
For multiplication, product, times, etc.
For subtraction, difference, less than, minus, etc.
And for division, look for quotient, divide, etc.
Hope this helps : )
How to find the area of the shaded polygon? Will give brainliest! Thank you!

Answers
A=200in² is the area of the shaded polygon so 200in² ➗ 30in
Erin buys 3 packs of potatoes costing £2 each, 4 packs of carrots for £2 per pack, and 4 turnips costing 90p each. If she pays with a £20 note, how much change would she get in pounds, £?
Answers
Answer: £2.4
Step-by-step explanation:
From the question, Erin buys 3 packs of potatoes costing £2 each, 4 packs of carrots for £2 per pack, and 4 turnips costing 90p each.
Total cost of potatoes = 3 × £2 = £6
Total cost of carrots = 4 × £2 = £8
Total cost of turnips = 4 × 90p = £360p = £3.6
The total cost of things bought by Erin will now be:
= £6 + £8 + £3.6
= £17.6
If she pays with a £20 note, she will collect a change of:
= £20 - £17.6
= £2.4
= 2 pounds, 40 pennies.
solve the equation for all real solutions
4q^2-4q+1=0

Answers
Answer:
q= 1/2 or 0.5 depending
Step-by-step explanation:
d²v dt² v=2t² +7t+11 Find
Answers
The second derivative of v with respect to t, denoted as d²v/dt², is equal to 4
The second derivative of v with respect to t, we will differentiate v twice.
v = 2t² + 7t + 11
First, let's find the first derivative of v with respect to t (dv/dt):
dv/dt = d/dt (2t² + 7t + 11)
Using the power rule of differentiation, we differentiate each term separately:
dv/dt = 2(2t) + 7(1) + 0
dv/dt = 4t + 7
Now, let's find the second derivative of v with respect to t (d²v/dt²):
d²v/dt² = d/dt (4t + 7)
Again, using the power rule of differentiation, we differentiate each term separately:
d²v/dt² = 4(1) + 0
d²v/dt² = 4
Therefore, the second derivative of v with respect to t, denoted as d²v/dt², is equal to 4.
To know more about second derivative click here :
https://brainly.com/question/29090070
#SPJ4
the distance from the epicenter of the march 1964 earthquake to crescent city is 2600 kilometers. how long did it take the first p-wave to reach crescent city
Answers
The distance from the epicenter of the march 1964 earthquake to crescent city is 2600 kilometers and It took 400 seconds for the first p-wave to reach crescent city
In a seismic event like an earthquake, seismic waves propagate through the Earth at different speeds. The first type of seismic wave to reach a particular location is the primary wave, or P-wave. P-waves are compressional waves that travel faster than other seismic waves, such as S-waves or surface waves.
To calculate the time it took for the P-wave to reach Crescent City, we need to know the speed at which P-waves travel. On average, P-waves travel at a speed of about 6-7 kilometers per second in the Earth's crust. However, this speed can vary depending on the specific properties of the Earth's layers.
Using an average speed of 6.5 kilometers per second, we can calculate the time it took for the P-wave to travel a distance of 2600 kilometers:
Time = Distance / Speed = 2600 km / 6.5 km/s ≈ 400 seconds.
Therefore, it took approximately 400 seconds, or 6 minutes and 40 seconds, for the P-wave to reach Crescent City from the epicenter of the March 1964 earthquake.
It is important to note that the calculated time is an estimation based on average values, and the actual time may vary depending on the specific geological conditions along the propagation path of the P-wave.
Know more about epicenter here:
https://brainly.com/question/4052993
#SPJ8
Reflect the figure over the line
y
=
−
1
y=−1.
Answers
Answer:
Step-by-step explanation:

Simplify (5x² + 3x + 4) + (2x² − 6x + 3). (1 point)
O 7x² +9x+7
7x²+3x+7
O7x²-3x+1
7x²-3x+7
Answers
Step-by-step explanation:
5×3+4 =19
2-6+3=5
19+5
=24
HELP ASAP WILL MARK BRAINLIEST
Which equation is true?

Answers
Answer:
C Hope this helps This may be wrong though
Step-by-step explanation:
In a _______ , _______, not all members of a population have an equal probability of being included?
In an _______, _______, all members of the population have an equal probability of being included.
Some associations are stronger than others, what describes the strength of the association?
A) Effect Size B) Bivariate correlations C) Correlational Samples D) None of the Above
Curvilinear association is one in which the correlation coefficient is zero (or close to zero) and the relationship between two variables isn't a straight line? True/ False
Answers
In a nonprobability sampling, not all members of a population have an equal probability of being included.
In a probability sampling, all members of the population have an equal probability of being included.
The strength of the association is described by the effect size.
Curvilinear association is one in which the correlation coefficient is zero (or close to zero) and the relationship between two variables isn't a straight line. False.
In nonprobability sampling, the selection of individuals from the population is not based on random sampling principles. This means that not all members of the population have an equal probability of being included in the sample.
In probability sampling, every member of the population has an equal and known chance of being selected for the sample. Random sampling methods, such as simple random sampling, stratified random sampling, and cluster sampling, are commonly used to achieve this. In probability sampling, the sample is representative of the population, and statistical inferences can be made.
The strength of the association between two variables is typically measured by the effect size. Effect size quantifies the magnitude or magnitude of the relationship between variables and provides an indication of the practical or substantive significance of the association.
Curvilinear association refers to a relationship between two variables that cannot be adequately described by a straight line. In such cases, the correlation coefficient between the variables may be zero or close to zero, indicating no linear relationship.
Nonprobability sampling involves selecting individuals without an equal probability of inclusion, while probability sampling ensures that all members of the population have an equal chance of being included. The strength of the association between variables is described by the effect size, and a curvilinear association indicates a non-straight line relationship between variables.
To know more about probability, visit;
https://brainly.com/question/23417919
#SPJ11
Si el decrecimiento o crecimiento en las exportaciones de la palta a España y Estados Unidos, respectivamente, continuara como en el año 2012, ¿en cuánto tiempo coincidirían los valores de las exportaciones
hacia ambos países?
ayuda le doy corona
Answers
It would take roughly 13.86 times for the import values to coincide if the drop or growth in avocado exports to Spain and the United States.
To answer this question, we'd need to have specific data about the drop or growth rates of avocado exports to Spain and the United States in 2012, as well as the current import values for both countries. Without this information, it isn't possible to directly prognosticate how long it would take for the import values to coincide.
Assuming we have the necessary data, we can use the following formula to calculate the time it would take for the import values to coincide
t = ln( P2/ P1)/ ln( 1 r)
where t is the time it would take for the import values to coincide, P1 is the original import value, P2 is the final import value, and r is the growth rate.
For illustration, if we know that the original import value for avocado exports to Spain was$ 100 million in 2012, and it dropped at a rate of 5 per time, and the original import value for avocado exports to the United States was$ 200 million in 2012, and it increased at a rate of 10 per time, we can calculate how long it would take for their import values to coincide
For Spain P1 = $ 100 million, r = -0.05
For the US P1 = $ 200 million, r = 0.1
Assuming the final import values for both countries would be the same, we can set P2 equal to each other
ln( P2/$ 100 million)/ ln(0.95) = ln($ 200 million/ P2)/ ln(1.1)
working for P2, we get
P2 = $141.42 million
Substituting this value into the formula, we get
t = ln($141.42 million/$ 100 million)/ ln(0.95) = 13.86 times
thus, it would take roughly 13.86 times for the import values to coincide if the drop or growth in avocado exports to Spain and the United States, independently, continued as in 2012. still, this is just an academic illustration grounded on certain hypotheticals, and the factual time it would take for the import values to coincide would depend on the specific data for each country.
Learn more about exports;
https://brainly.com/question/13663581
#SPJ4
The complete question in English is-
If the decrease or growth in avocado exports to Spain and the United States, respectively, continued as in 2012, how long would the export values coincide in both countries?
three numbers in an arithmetic progression have a sum of 39 and a product of 2145. find the smallest number of that progression.
Answers
Thus, the three terms of an arithmetic progression are (8, 13, and 18) or, (9, 13, and 17).
Let three terms of an arithmetic progression = (a - d), a, ( a + d)
According to the question:
The sum of three terms of an arithmetic progression = 39
∴ (a - d) + a + ( a + d) = 39
⇒ 3a = 39
⇒ a = 13
Also, The product of three terms of an arithmetic progression = 2145
∴ (a - d)a( a + d) = 2145
⇒ a(a^2 - d^2) = 2145
Put a = 13, and we get
d=4
Three terms of an arithmetic progression = (13 - 4), 13 and ( 13 + 4)
= 9,13,17
Put a = 13 and d = 4
Thus, the three terms of an arithmetic progression are (8, 13, and 18) or, (9, 13, and 17).
learn more about arithmetic progression
https://brainly.com/question/30364336
#SPJ4
A significance test about a proportion is conducted using a significance level of 0.05. The sample statistic is 0.12. The p-value is 0.03? a) If H0 were true, for what probability of a Type I error was the test designed?
b) What conclusion (reject or fail to reject) would you make for this test?
c) If this test resulted in a decision error, what type of error was it?
Answers
Answer: 28282
Step-by-step explanation:
I think
Look at photo attached
which function is the inverse of f(x) = b^x?
Answers
The inverse function of f(x) = \(b^x\) is g(x) = log_b(x), where log_b denotes the logarithm with base b. Therefore, g(x) is the inverse function of f(x) = \(b^x.\)
The inverse function of an exponential function f(x) =\(b^x\) is a logarithmic function g(x) = log_b(x), where the base of the logarithm matches the base of the original exponential function.
To find the inverse function, we switch the roles of x and y in the original function and solve for y. So, for f(x) = \(b^x\), we rewrite it as x = \(b^y\) and solve for y. Taking the logarithm of both sides with base b, we get log_b(x) = y, which can be written as g(x) = log_b(x).
The inverse function undoes the effect of the original function. In this case, the exponential function f(x) = \(b^x\) raises the base b to the power of x, while the inverse function g(x) = log_b(x) "undoes" the exponentiation by taking the logarithm base b of x, resulting in the original input value x. Therefore, g(x) is the inverse function of f(x) = \(b^x.\)
Learn more about logarithm here:
https://brainly.com/question/30226560
#SPJ11
Find the inverse function of f(x) = \(b^x\)
Find the equation of the tangent line to the curve y = (8 ln(x))/x at the points (1, 0) and (e, 8/e).
Answers
The equation of the tangent line to the curve are \(y=x-1 , y=\frac{xe-e^{2}+8 }{e}\).
It is required to find the solution.
What is a tangent ?A tangent is a line that touches the edge of a curve or circle at one point, but does not cross it. The tangent line to a curve at a point is that straight line that best approximates (or “clings to”) the curve near that point.
Given:
\(y=8\frac{lnx}{x} \\\\y'=8(\frac{1/x*x-lnx*1}{x^{2} } \\\\y'=\frac{1-lnx}{x^{2} }\)
Now, we find the slope of the tangent by inserting the point (1,0) into the derivative.
\(m_{tangent}=\frac{1-ln1}{1^{2} }\\\\m_{tangent}=1-0/1\\\\m_{tangent} =1\)
We can now find the equation, because we know the slope and a point (1, 0).
\(y-y_{1} =m(x-x_{1} )\\\)
y-0=1(x-1)
y=x-1
We can now find the equation, because we know the slope and a point (e, 8/e).
\(y-y_{1} =m(x-x_{1} )\\\\y-8/e=1(x-e)\\\\y=\frac{xe-e^{2}+8 }{e}\)
Therefore, the equation of the tangent line to the curve are \(y=x-1 , y=\frac{xe-e^{2}+8 }{e}\).
Learn more about tangent here:
https://brainly.com/question/19064965
#SPJ4
Choose one value that is in the domain of both y(x) = x² and y² = x and that is greater than
0. Substitute that value into y(x) = x² and y² = x and then simplify. Explain how your answers
help to show that the graph on the left represents a function while the graph on the right
represents a relation. Show your work and use function notation where possible
I
Answers
We take the value 2 for which y(2)=4 and \(y^{2}\)=2 and see that y(x)=\(x^{2}\) is a function and \(y^{2}\)=x is a relation.
Domain is the set of values that a variable can take in an algebraic expression.For the equation y(x)=\(x^{2}\), x can take any value from negative infinity to positive infinity so we can say that the domain for x is (-∞,∞). For the equation \(y^{2}\)=x, x can take any value greater than or equal to zero. Since x=\(y^{2}\) we can't take a negative value for x because squared numbers are always positive, so the domain of x will be [0,∞). The common domain for both the equations is [0,∞). Let us choose a value from this common domain,let's say 2. Then for
y(x)=\(x^{2}\)⇒y(2)=4 ...(i)
\(y^{2} =x\)=2 then y=±\(\sqrt{2}\)...(ii)
A function always has an output variable and one or more input variables.For first equation, y is the output variable and x is the input variable. A relation states that two expressions are equal and one is not dependant on another. For equation (i) y is dependant on x but in equation (ii) both the variables are independant.
Thus we can conclude that y(x)=\(x^{2}\) is a function and \(y^{2}\)=x is a realtion.
Learn more about functions and realtions here:
https://brainly.com/question/2253924
#SPJ9